갈래비
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
갈래비는 원자, 분자 및 광학 물리학 분야에서 여기 상태로부터 특정 하위 에너지 상태로의 붕괴 확률을 의미한다. 여기 상태에서 바닥 상태 또는 수명이 긴 상태로 붕괴될 때, 특정 상태로 붕괴될 확률을 분기율이라고 하며, 여러 붕괴 가능성이 있는 경우 각 확률의 합은 1이다. 분기율 대신 분기 비를 사용하기도 하며, 이는 두 상태 간의 분기율의 비율이다. 분기율은 원자의 형광을 시간 분해능으로 기록하는 등 다양한 방법으로 측정할 수 있다.
더 읽어볼만한 페이지
- 핵물리학 - 핵분열
핵분열은 원자핵이 중성자와 충돌하여 두 개 이상의 조각으로 분열되는 현상으로, 막대한 에너지를 방출하며 원자력 발전과 핵무기에 응용되지만 방사성 폐기물 처리 등의 문제점을 가지고 있다. - 핵물리학 - 알파 붕괴
알파 붕괴는 원자핵이 헬륨-4 원자핵인 알파 입자를 방출하여 원자 번호와 질량수가 감소하는 방사성 붕괴의 한 형태로, 무거운 원자핵에서 주로 발생하며 양자 터널링 효과로 설명되고 연기 감지기 등에 활용되지만 인체에 유해할 수도 있다. - 입자물리학 - 전자볼트
전자볼트는 전자가 1볼트의 전위차를 통과할 때 얻거나 잃는 에너지 단위로, 1.602 × 10⁻¹⁹ 줄과 같으며, 다양한 물리학 분야와 공학에서 에너지, 질량, 운동량, 온도, 거리 등을 표현하는 데 널리 활용된다. - 입자물리학 - 알파 붕괴
알파 붕괴는 원자핵이 헬륨-4 원자핵인 알파 입자를 방출하여 원자 번호와 질량수가 감소하는 방사성 붕괴의 한 형태로, 무거운 원자핵에서 주로 발생하며 양자 터널링 효과로 설명되고 연기 감지기 등에 활용되지만 인체에 유해할 수도 있다.
| 갈래비 |
|---|
2. 원자 상태의 분기율
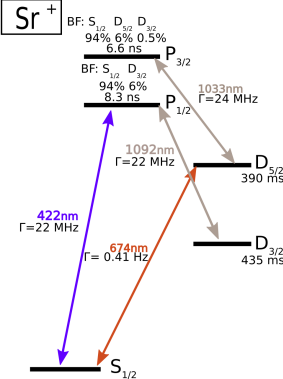
원자, 분자 및 광학 물리학에서 분기율은 어떤 여기 상태에서 특정 하위 에너지 상태로 붕괴될 확률을 나타낸다. 예를 들어 원자 시스템에서 여기 상태 |e>영어는 바닥 상태 |g>영어나 수명이 긴 상태 |d>영어로 붕괴할 수 있다. 이때 |g>영어 상태로 붕괴될 확률이 ''p''라면, 다른 상태 |d>영어로 붕괴될 확률은 ''1-p''가 된다.[2]
2. 1. 분기율의 정의
원자, 분자 및 광학 물리학 분야에서 분기율은 어떤 여기 상태로부터 특정 하위 에너지 상태로의 붕괴 확률을 의미한다. 원자 시스템에서 여기 상태 |e>영어로의 전이를 유도한다고 가정하면, 이 상태는 바닥 상태 |g>영어 또는 수명이 긴 상태 |d>영어로 붕괴될 수 있다. |g>영어 상태로 붕괴될 확률(분기율)이 ''p''이면, 다른 상태 |d>영어로 붕괴될 확률은 ''1-p''가 된다.[2] 추가적인 붕괴 가능성은 적절하게 분할되며, 해당 확률의 합은 1이 된다.경우에 따라 분기율 대신 분기 비가 사용된다. 이 경우 분기 비는 두 상태 간의 분기율의 비율일 뿐이다. 이전의 예시를 사용하면, |g>영어 상태로의 분기율이 ''p''일 때, |g>영어와 |d>영어로의 전이율을 비교하는 분기 비는 ''p/(1-p)''가 된다.
2. 2. 분기비 (Branching Ratio)
원자, 분자 및 광학 물리학 분야에서 분기율은 어떤 여기(들뜬) 상태로부터 특정 하위 에너지 상태로의 붕괴 확률을 의미한다. 원자 시스템에서 여기 상태 |e>영어로의 전이를 유도한다고 가정하면, 이 상태는 바닥 상태 |g>영어 또는 수명이 긴 상태 |d>영어로 붕괴될 수 있다. |g>영어 상태로 붕괴될 확률(분기율)이 p영어이면, 다른 상태 |d>영어로 붕괴될 확률은 1-p영어가 된다.[2] 추가적인 붕괴 가능성은 적절하게 분할되며, 해당 확률의 합은 1이 된다.경우에 따라 분기율 대신 분기비가 사용된다. 이 경우 분기비는 두 상태 간의 분기율의 비율일 뿐이다. 이전의 예시를 사용하면, |g>영어 상태로의 분기율이 p영어일 때, |g>영어와 |d>영어로의 전이율을 비교하는 분기비는 p/(1-p)영어가 된다.
3. 분기율 측정
분기율은 관련 상태에서 일련의 개체군 이동 동안 원자의 형광을 시간 분해능으로 기록하는 것을 포함하여 다양한 방법으로 측정할 수 있다.[3][2] 3상태 Λ|-영어시스템에서 측정 절차는 하위 문단을 참고하라.
3. 1. 3상태 Λ-시스템에서의 측정 절차
기저 상태 g영어, 여기 상태 e영어, 그리고 수명이 긴 상태 d영어를 포함하는 3상태 Λ-시스템의 측정 절차는 다음과 같다.[3][2]먼저, 모든 원자를 기저 상태로 준비한다. 기저 상태와 여기 상태 사이의 전이를 구동하는 펌프 레이저를 켠 다음, 광전자 증배관(PMT)을 사용하여 전이 중에 방출되는 "파란색 광자"를 계산한다. 계산된 파란색 광자를 N으로 기록한다.
원자가 여기 상태로 구동될 때마다 수명이 긴 상태로 붕괴될 확률은 1-p이다. 따라서 펌프 레이저가 켜져 있는 동안 점점 더 많은 원자가 냉각 레이저로 접근할 수 없는 수명이 긴 상태에 도달하게 된다.
모든 원자가 d영어 상태에 있으면, d영어와 e영어 사이의 전이를 구동하는 재펌프 레이저를 적용한다. 이 과정에서 각 원자는 하나의 파란색 광자를 방출한다. 이 과정에서 방출된 파란색 광자의 수를 n으로 나타낸다.
그러면 e영어가 g영어로 붕괴되는 분기비는 다음과 같다.
:
참조
[1]
서적
branching fraction
[2]
논문
Precision measurement method for branching fractions of excited P(1/2) states applied to 40Ca+
2013-07-12
[3]
논문
Iterative precision measurement of branching ratios applied to 5 P states in 88 Sr +
2016-12-15
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com