감산기

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 반감산기 (Half Subtractor)
3. 전감산기 (Full Subtractor)
참조

1. 개요

감산기는 뺄셈을 수행하는 데 사용되는 디지털 논리 회로이다. 감산기는 반감산기와 전감산기로 나뉜다. 반감산기는 두 개의 입력 비트의 뺄셈을 수행하며, 전감산기는 세 개의 입력 비트의 뺄셈을 수행한다. 각 감산기는 차이(difference)와 빌림(borrow)을 출력한다.

더 읽어볼만한 페이지

디지털 전자공학 - 트랜지스터-트랜지스터 논리
트랜지스터-트랜지스터 논리(TTL)는 1961년 제임스 L. 부이에 의해 발명된 바이폴라 접합 트랜지스터 기반의 디지털 회로 기술로, 텍사스 인스트루먼츠의 7400 시리즈를 통해 널리 사용되었으며, 저렴한 비용으로 디지털 기술 발전에 기여했다.
디지털 전자공학 - 플립플롭
플립플롭은 1비트 이상의 정보를 저장하는 디지털 논리 회로로, 에클스-조던 트리거 회로에서 기원하여 SR, D, T, JK 등 다양한 유형으로 구현되며, 컴퓨터 기억 장치의 기본 구성 요소로 사용되지만 타이밍 요소에 민감하게 설계해야 한다.
컴퓨터 산술 - IEEE 754
IEEE 754는 부동소수점 숫자를 표현하고 처리하기 위한 국제 표준으로, 다양한 형식과 연산, 반올림 규칙, 예외 처리 등을 정의한다.
컴퓨터 산술 - 1의 보수
1의 보수는 이진수에서 양수는 일반적인 이진수로, 음수는 양수의 각 비트를 반전시켜 표현하며, 덧셈 시 자리올림수가 발생하면 결과값에 더해야 하고, 0을 중복 표현하는 단점으로 현대에는 2의 보수가 주로 사용된다.

감산기

2. 반감산기 (Half Subtractor)

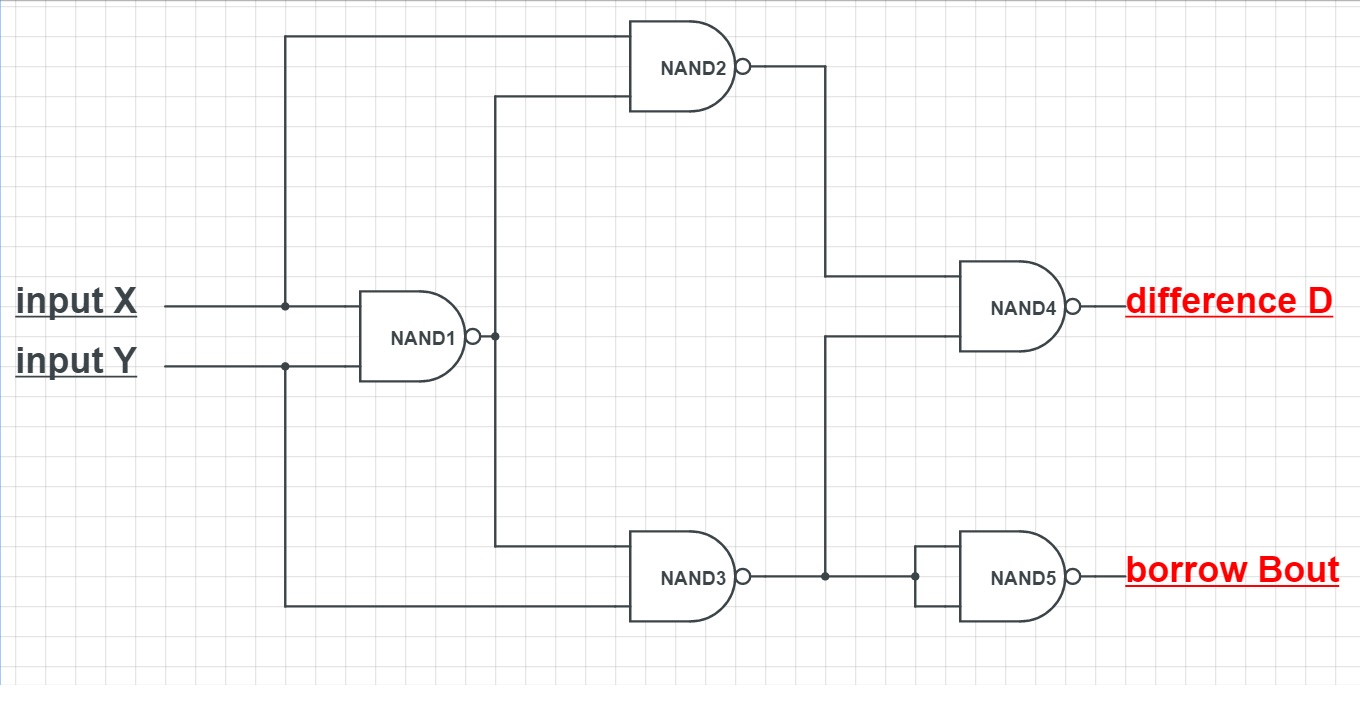
반감산기(Half Subtractor)는 두 개의 이진 입력 비트의 뺄셈을 수행하는 기본적인 조합 논리 회로이다. 입력으로는 피감수

X

와 감수

Y

를 받고, 출력으로는 두 비트의 차이(Difference)

D

와 빌림(Borrow out)

B_\text{out}

을 생성한다.

빌림 출력(

B_\text{out}

)은

X

에서

Y

를 뺄 때 상위 비트에서 빌려와야 하는 경우, 즉

X < Y

일 때 1이 된다. 입력

X

와

Y

가 단일 비트이므로, 빌림이 발생하는 유일한 경우는

X=0

이고

Y=1

일 때이다. 반감산기는 XOR 게이트, AND 게이트, NOT 게이트 등을 조합하여 구현할 수 있으며, NAND 게이트만으로도 구현 가능하다.

반감산기의 동작 원리와 구체적인 논리식, 진리표는 하위 섹션에서 더 자세히 설명한다.

2. 1. 반감산기의 구조와 원리

반감산기는 두 비트의 뺄셈을 수행하는 조합 회로이다. 그림 1과 2에서 볼 수 있듯이 조합 부울 논리 회로를 통해 설계할 수 있다. 반감산기는 두 개의 입력, 즉 피감수

X

와 감수

Y

를 받아서 두 개의 출력, 즉 차이(Difference)

D

와 빌림(Borrow out)

B_\text{out}

을 생성한다.

빌림 출력(

B_\text{out}

) 신호는

X

에서

Y

를 뺄 때 상위 자릿수에서 빌림이 필요한 경우, 즉

X < Y

일 때 1이 된다. 입력

X

와

Y

가 각각 한 비트이므로, 빌림이 발생하는 경우는 오직

X = 0

이고

Y = 1

일 때뿐이다. 따라서 빌림 출력의 논리식은 다음과 같다.

:

B_{\text{out}} = \overline{X} \cdot Y

이 식은 AND 게이트와 NOT 게이트를 이용하여 구현할 수 있다. 그림 1의 회로도는

X - Y

연산을 수행하며,

Y - X

연산과는 다르다는 점에 유의해야 한다.

차이(

D

) 비트는 XOR 게이트를 사용하여 계산된다. XOR 게이트는 두 입력이 서로 다를 때 1을 출력하는데, 이는 뺄셈의 결과 비트와 동일하다.

:

D = X \oplus Y

뺄셈 자체는 교환 법칙이 성립하지 않지만, 차이 비트

D

는 교환 법칙이 성립하는 XOR 연산으로 계산된다는 점이 중요하다.

반감산기는 NAND 게이트만으로도 구현할 수 있다 (그림 2).

반감산기의 동작을 요약한 진리표는 다음과 같다.

입력		출력
X	Y	D	B_out
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

이 진리표와 카르노 맵 등을 이용하면 위에서 제시된 $D$ 와 $B_\text{out}$ 의 논리 방정식을 유도할 수 있다.

결과적으로, 교차 추적을 피하고 부정 게이트를 회피하는 간소화된 반감산 회로는 다음과 같이 표현할 수 있다.



X ── XOR ─┬─────── |X-Y|,  X와 Y가 같으면 0, 그렇지 않으면 1

┌──┘   └──┐

Y ─┴─────── AND ── 빌림, Y > X이면 1, 그렇지 않으면 0

여기서 오른쪽 줄은 출력이고, 나머지(위, 아래 또는 왼쪽)는 입력이다.

2. 2. 반감산기의 진리표

반감산기는 두 개의 입력, 피감수

X

와 감수

Y

를 가지며, 두 개의 출력, 차이

D

와 빌림 출력

B_\text{out}

을 가진다. 빌림 출력 신호는 감산기가 다자릿수 뺄셈에서 다음 자릿수에서 빌려야 할 때 설정된다. 즉,

X < Y

일 때

B_{\text{out}} = 1

이다.

X

와

Y

는 비트이므로,

X = 0

이고

Y = 1

일 때만

B_\text{out} = 1

이다.

반감산기의 진리표는 다음과 같다.

입력		출력
X	Y	D	B_out
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

위의 표와 카르노 맵을 사용하여 $D$ 와 $B_\text{out}$ 에 대한 다음 논리 방정식을 찾는다.

: $D = X \oplus Y$

: $B_\text{out} = \overline X \cdot Y$

결과적으로, 특히 교차 추적을 피하고 부정 게이트를 회피하는 간소화된 반감산 회로는 다음과 같다.

:



X ── XOR ─┬─────── |X-Y|,  X와 Y가 같으면 0, 그렇지 않으면 1

┌──┘   └──┐

Y ─┴─────── AND ── 빌림, Y > X이면 1, 그렇지 않으면 0

여기서 오른쪽 줄은 출력이고, 나머지(위, 아래 또는 왼쪽에서)는 입력이다.

2. 3. 반감산기의 논리식

반감산기는 두 개의 입력, 피감수

X

와 감수

Y

를 가지며, 두 개의 출력, 차이

D

와 빌림 출력

B_\text{out}

을 가진다. 빌림 출력 신호(

B_\text{out}

)는 감산기가 다자릿수 뺄셈에서 다음 자릿수에서 빌려야 할 때 설정되는데, 이는

X < Y

일 때, 즉

X = 0

이고

Y = 1

일 때만

B_{\text{out}} = 1

이 되는 경우이다.

반감산기의 진리표는 다음과 같다.

입력		출력
X ! Y ! D ! B_out
0 \| 0 \| 0
1 \| 1 \| 1
0 \| 1 \| 0
1 \| 0 \| 0

위의 진리표와 카르노 맵 등을 이용하여 차이( $D$ )와 빌림 출력( $B_\text{out}$ )에 대한 다음의 논리 방정식을 유도할 수 있다.

: $D = X \oplus Y$

: $B_\text{out} = \overline X \cdot Y$

여기서 차이 비트 $D$ 는 XOR 게이트를 사용하여 계산된다. 뺄셈 자체는 교환 법칙을 따르지 않지만, 차이 비트 $D$ 는 교환 법칙이 적용되는 XOR 연산으로 계산된다는 점이 중요하다. 빌림 출력 $B_\text{out}$ 는 $X$ 가 0이고 $Y$ 가 1일 때만 1이 되는 AND 연산( $\overline X \cdot Y$ )으로 표현된다.

결과적으로, 교차 추적을 피하고 부정 게이트를 회피하는 간소화된 반감산 회로는 다음과 같이 나타낼 수 있다.



X ── XOR ─┬─────── |X-Y|,  X와 Y가 같으면 0, 그렇지 않으면 1

┌──┘   └──┐

Y ─┴─────── AND ── 빌림, Y > X이면 1, 그렇지 않으면 0

위 회로도에서 오른쪽 줄은 출력이고, 나머지(위, 아래 또는 왼쪽에서)는 입력이다.

3. 전감산기 (Full Subtractor)

전감산기(Full Subtractor)는 세 개의 입력 비트인 피감수 $X$ , 감수 $Y$ , 그리고 이전 자리에서의 빌림 여부를 나타내는 빌림 입력 $B_\text{in}$ 을 받아 뺄셈 연산을 수행하는 조합 회로이다. 이 회로는 연산 결과로 현재 자리의 차이(Difference) $D$ 와 다음 상위 자리로 빌려줘야 할지 여부를 나타내는 빌림 출력(Borrow-out) $B_\text{out}$ 이라는 두 개의 출력 비트를 생성한다. 즉, 전감산기는 이전 자리에서의 빌림( $B_\text{in}$ )까지 고려하여 뺄셈( $X - Y - B_\text{in}$ )을 수행하고, 그 결과( $D$ )와 다음 자리로 넘겨줄 빌림( $B_\text{out}$ )을 계산한다.

3. 1. 전감산기의 구조와 원리

전감산기는 세 개의 입력 비트인 피감수

X

, 감수

Y

, 그리고 이전 자리에서의 빌림 여부를 나타내는 빌림 입력

B_\text{in}

을 받아 뺄셈을 수행하는 조합 회로이다. 전감산기는 연산 결과로 차이(Difference)

D

와 다음 자리로의 빌림 여부를 나타내는 빌림 출력

B_\text{out}

이라는 두 개의 출력 비트를 생성한다.

B_\text{in}

은 이전 자릿수에서 현재 자릿수의 피감수

X

로부터 값을 빌려왔을 경우 1이 된다. 따라서 전감산기는

X

에서

Y

뿐만 아니라

B_\text{in}

까지 빼는 연산, 즉

X - Y - B_\text{in}

을 수행한다.

반감산기와 마찬가지로, 전감산기는 현재 자리의 연산을 위해 다음 상위 자릿수에서 빌려와야 할 경우 빌림 출력(

B_\text{out}

)을 생성한다.

X

에서

Y

와

B_\text{in}

을 빼야 하므로,

X

가

Y + B_\text{in}

보다 작을 때(

X < Y + B_\text{in}

) 빌림이 필요하게 되어

B_\text{out}

이 1이 된다. 빌림 출력(

B_\text{out}

)이 발생하면, 이는 현재 자릿수에 2 (이진법의 밑)를 더하는 것과 같다. 이는 십진법 뺄셈에서 빌림이 발생할 때 10을 더하는 것과 유사한 원리이다. 따라서 차이

D

는

D = X - Y - B_\text{in} + 2B_\text{out}

으로 계산된다.

전감산기의 동작을 나타내는 진리표는 다음과 같다.

입력			출력
X (피감수)	Y (감수)	B_in (빌림 입력)	D (차이)	B_out (빌림 출력)
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

위 진리표로부터 전감산기의 출력 $D$ 와 $B_\text{out}$ 에 대한 논리식은 다음과 같이 유도될 수 있다.

$D=X\oplus Y\oplus B_{in}$

$B_{out}=\bar{X}B_{in}+\bar{X}Y+YB_{in}$

여기서 $\oplus$ 는 XOR 연산을, $\bar{X}$ 는 $X$ 의 NOT 연산을, +는 OR 연산을, 생략된 곱셈 기호는 AND 연산을 의미한다.

3. 2. 전감산기의 진리표

전감산기는 세 개의 입력 비트인 피감수

X

, 감수

Y

, 이전 자리 빌림

B_\text{in}

의 뺄셈을 수행하는 조합 회로이다. 전감산기는 차이

D

와 다음 자리 빌림

B_\text{out}

이라는 두 개의 출력 비트를 생성한다.

B_\text{in}

은 이전 자릿수에서

X

로 빌림이 발생했을 때 1이 된다. 따라서

B_\text{in}

은 감수

Y

와 함께

X

에서 빼야 할 값이 된다. 이를 수식으로 표현하면

X - Y - B_\text{in}

이다. 전감산기는 다음 자릿수에서 빌려야 할 때 빌림 출력(

B_\text{out}

)을 생성하는데, 이는

X < Y + B_\text{in}

일 때 발생한다. 빌림 출력이 발생하면 현재 자릿수 계산에 2가 더해진 것으로 간주한다(뺄셈 결과

D = X - Y - B_\text{in} + 2B_\text{out}

). 이는 십진법 뺄셈에서 윗자리에서 10을 빌려오는 것과 유사하다.

전감산기의 진리표는 다음과 같다.

입력			출력
X (피감수)	Y (감수)	B_in (이전 자리 빌림)	D (차이)	B_out (다음 자리 빌림)
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

진리표에 따른 논리 방정식은 다음과 같다.

$D=X\oplus Y\oplus B_{in}$

$B_{out}=\bar{X}B_{in}+\bar{X}Y+YB_{in}$

3. 3. 전감산기의 논리식

전가산기는 세 개의 입력 비트인 피감수

X

, 감수

Y

, 이전 자리에서의 빌림 입력

B_\text{in}

을 받아 뺄셈 연산을 수행하는 조합 회로이다. 전가산기는 연산 결과로 차이(Difference)

D

와 다음 자리로의 빌림 출력(Borrow-out)

B_\text{out}

이라는 두 개의 출력 비트를 생성한다. 빌림 입력

B_\text{in}

은 이전 자리의 연산에서 빌림이 필요했을 때 1이 되며, 이 값은 피감수

X

에서 감수

Y

와 함께 빼지게 된다. 즉,

X - Y - B_\text{in}

연산을 수행한다.

반가산기와 마찬가지로, 전가산기는 현재 자리의 연산 결과, 다음 상위 자리에서 빌려와야 할 필요가 있을 때 빌림 출력

B_\text{out}

을 1로 설정한다. 빌림은

X

에서

Y

와

B_\text{in}

의 합을 뺄 때,

X

가

Y + B_\text{in}

보다 작을 경우(

X < Y + B_\text{in}

) 발생한다. 빌림이 발생하면(

B_\text{out} = 1

), 현재 자리의 계산에는 2 (해당 자릿값)가 더해진 것으로 간주한다. 이는 십진법 뺄셈에서 빌림이 발생할 때 10을 더하는 것과 유사한 원리이다. 따라서 차이

D

는

D = X - Y - B_\text{in} + 2B_\text{out}

의 관계를 만족한다.

전감산기의 입력과 출력 관계는 다음 진리표로 나타낼 수 있다.

입력			출력
X (피감수)	Y (감수)	B_in (빌림 입력)	D (차이)	B_out (빌림 출력)
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

위 진리표를 바탕으로 전감산기의 출력 $D$ 와 $B_\text{out}$ 에 대한 논리식을 유도하면 다음과 같다.

'''차이 (D):''' $D=X\oplus Y\oplus B_{in}$
'''빌림 출력 (B_out):''' $B_{out}=\bar{X}B_{in}+\bar{X}Y+YB_{in}$

여기서

\oplus

는 XOR 연산을,

\bar{X}

는 NOT 연산을, '+'는 OR 연산을, 변수들이 붙어있는 것은 AND 연산을 의미한다.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com

입력		출력
X ! Y ! D ! B_out
0 \| 0 \| 0
1 \| 1 \| 1
0 \| 1 \| 0
1 \| 0 \| 0