격자 경로

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 북동(NE) 격자 경로
4. 격자 경로의 수 세기
참조

1. 개요

격자 경로는 정수 격자 내에서 정의되는 점들의 순열로, 특정 보폭을 사용하여 점들을 연결한다. 특히 북동(NE) 격자 경로는 2차원 격자에서 동쪽과 북쪽으로만 이동하는 경로를 의미하며, 순열 단어로 표현할 수 있다. 격자 경로는 딕 경로, 슈뢰더 경로 등 다양한 조합 객체의 수를 세는 데 활용되며, 조합론과 밀접한 관련이 있다. 예를 들어, NE 격자 경로는 이항 계수를 통해 조합의 수를 계산하는 데 사용되며, 파스칼의 삼각형과 연결된다.

2. 정의

길이 $n$ , 보폭 $S\subseteq\mathbb Z^d$ 의 '''격자 경로'''는 $v_i-v_{i-1}\in S$ ( $i=1,\dots,n$ )를 만족시키는 점렬 $\{v^{(0)},v^{(1)},\dots,v^{(n)}\}\subset\mathbb Z^d$ 이다.^[6]

3. 북동(NE) 격자 경로

'''북동(NE) 격자 경로'''는 $\mathbb{Z}^2$ 에서 $S = \lbrace (0,1), (1,0) \rbrace$ 단계를 가지는 격자 경로이다. $(0,1)$ 단계는 북쪽(N) 단계, $(1,0)$ 단계는 동쪽(E) 단계라고 한다.^[6]

NE 격자 경로는 일반적으로 원점에서 시작한다. 이러한 경우, NE 격자 경로 $L$ 의 모든 정보는 순열 단어로 표현할 수 있다. 순열 단어의 길이는 격자 경로의 단계 수( $k$ )를 나타내며, $N$ 과 $E$ 의 순서는 $L$ 의 단계를 나타낸다. 또한, 순열 단어 내 $N$ 의 수와 $E$ 의 수는 $L$ 의 끝점을 결정한다.

원점에서 시작하는 NE 격자 경로의 순열 단어에 $n$ 개의 $N$ 단계와 $e$ 개의 $E$ 단계가 포함되어 있다면, 경로는 반드시 $(e,n)$ 에서 끝난다. 이는 경로가 $(0,0)$ 에서 정확히 $n$ 단계 북쪽과 $e$ 단계 동쪽으로 이동하기 때문이다.

정확히 하나의 $N$ 과 세 개의 $E$ 로 시작하는 네 개의 NE 격자 경로. 끝점은 반드시 $(3,1)$ 에 있다.

4. 격자 경로의 수 세기

격자 경로는 여러 조합 객체의 수를 세는 데 사용될 수 있으며, 특정 종류의 격자 경로의 수를 세는 조합 객체도 존재한다.

원점과 점 $v\in\mathbb Z^d$ 사이에서, 단위 벡터들 $\{e^{(1)},\dots,e^{(d)}\}$ 를 보폭으로 하는 격자 경로의 수는 다항 계수

: $\binom{v_1+\cdots+v_d}{v_1,\dots,v_n}=\frac{(v_1+\cdots v_d)!}{v_1!\cdots v_d!}$

이다.^[6] 특히, 원점과 점 $(a,b)\in\mathbb Z^2$ 사이에서, $\{(1,0),(0,1)\}$ 을 보폭으로 하는 격자 경로의 수는 이항 계수

: $\binom{a+b}a=\frac{(a+b)!}{a!b!}$

이다.

예를 들어, 위 그림과 같이 격자를 따라 동쪽 또는 남쪽으로만 이동하여 (0, 0)부터 (2, 3)까지 가는 경로의 수는 이항 계수를 사용하여

\binom 52=10

으로 계산할 수 있다.

딕 경로는 $n^{\text{번째}}$ 카탈랑 수 $C_n$ 로 세어진다.
슈뢰더 수는 단계가 $(1,0), (0,1)$ 및 $(1,1)$ 이고 대각선 $y=x$ 위로 절대 올라가지 않는, $(0,0)$ 에서 $(n,n)$ 까지의 격자 경로 수를 세어준다.^[2]
$(0,0)$ 에서 $(a,b)$ 까지의 NE 격자 경로의 수는 $a + b$ 개의 객체 집합에서 $a$ 개의 객체의 조합 수를 세어준다.

4. 1. 다이크 경로

다이크 경로는 원점과 점

(0,2n)

사이,

\{(1,1),(1,-1)\}

을 보폭으로 하는 격자 경로이거나, 원점과 점

(n,n)

사이의 단위 벡터 보폭의 격자 경로 가운데 대각선

y=x

위를 지나지 않는 경우로 간주할 수 있다. 다이크 경로의 수는 카탈랑 수

:

C_n=\frac1{n+1}\binom{2n}n=\frac{(2n)!}{(n+1)!n!}

이다.^[2] 딕 경로는

(0,0)

에서

(n,n)

까지의 NE 격자 경로이며, 대각선

y=x

아래에 엄격하게 놓여 있다(하지만 닿을 수 있음).^[2]^[3]

4. 2. 슈뢰더 경로

슈뢰더 수는 단계가 (1,0), (0,1) 및 (1,1)이고 대각선 y=x 위로 절대 올라가지 않는, (0,0)에서 (n,n)까지의 격자 경로 수를 센다.^[2]

4. 3. 조합과의 관련성

NE 격자 경로는 조합, 이항 계수, 파스칼의 삼각형과 밀접하게 관련되어 있다.

(0,0)

에서

(n,k)

까지의 격자 경로 수는 이항 계수

\binom{n+k}{n}

와 같다.^[6]

예를 들어, 격자를 따라 동쪽 또는 남쪽으로만 걸어 (0, 0)부터 (2, 3)까지 가는 경로의 수는 이항 계수

\binom 52=10

과 같다. 이와 같이 다른 점에 대해서도 같은 방식으로 수를 계산하여 그 점의 위치에 적으면 파스칼의 삼각형을 얻는다. 원점과 점

(a,b)\in\mathbb Z^2

사이에서

\{(1,0),(0,1)\}

을 보폭으로 하는 격자 경로의 수는 이항 계수

\binom{a+b}a=\frac{(a+b)!}{a!b!}

이다.

(0,0)

에서

(n,k)

까지의 격자 경로 수는 이항 계수

\binom{n+k}{n}

와 같다는 사실에서 파스칼의 삼각형을 유도할 수 있다. 다이어그램을 원점에 대해 시계 방향으로 135° 회전시키고 모든

n,k \in \mathbb{N} \cup \lbrace 0 \rbrace

를 포함하도록 확장하면 파스칼의 삼각형을 얻을 수 있는데, 이는 파스칼의 삼각형의

n

번째 행의

k

번째 항목이 이항 계수

\binom{n}{k}

이기 때문이다.

4. 3. 1. 예시: 조합 항등식 증명

우변

\binom{2n}{n}

은

(0,0)

에서

(n,n)

까지의 NE 격자 경로의 수와 같다. 이러한 각 NE 격자 경로는

x \in \lbrace 0, 1, \ldots, n \rbrace

에 대해 좌표가

(x, n-x)

인 격자점 중 정확히 하나와 교차한다.

n=4

인 경우, 아래 그림은

(0,0)

에서

(4,4)

까지의 모든 NE 격자 경로가 색칠된 노드 중 정확히 하나와 교차함을 보여준다.

좌변의 이항 계수 제곱인

\binom{n}{k}^2

은

(0,0)

에서

(k,n-k)

까지의 NE 격자 경로 집합의 두 복사본을 나타내며, 종착점과 시작점을 연결한다. 두 번째 복사본을 시계 방향으로 90° 회전해도 조합론은 변경되지 않는다.

\binom{n}{k} = \binom{n}{n-k}

이므로 격자 경로의 총 개수는 동일하게 유지된다.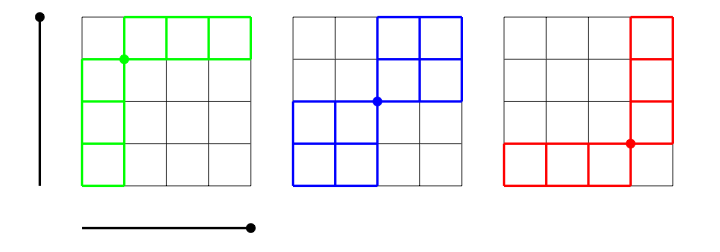

두 번째 복사본을 시계 방향으로 90° 회전한 NE 격자 경로 집합의 제곱.

아래 그림과 같이 NE 격자 경로의 제곱을 동일한 직사각형 배열에 겹쳐보면,

(0,0)

에서

(n,n)

까지의 모든 NE 격자 경로가 고려됨을 알 수 있다. 특히, 빨간색 격자점을 통과하는 모든 격자 경로는 격자 경로의 제곱 집합(빨간색으로 표시됨)에 의해 계산된다.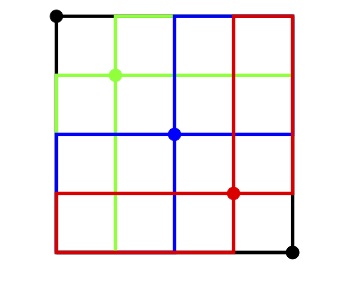

참조

_[1] 서적 Enumerative Combinatorics, Volume 1 Cambridge University Press 2012
_[2] 서적 Enumerative Combinatorics, Volume 2 Cambridge University Press 2001
_[3] 웹사이트 Wolfram MathWorld http://mathworld.wol[...] 2014-03-06
_[4] 서적 Lattice Path Combinatorics with Statistical Applications https://utorontopres[...] University of Toronto Press 1979-12-15
_[5] 서적 Lattice Path Combinatorics and Special Counting Sequences: From an Enumerative Perspective https://www.taylorfr[...] CRC Press 2024
_[6] 서적 Enumerative Combinatorics. Volume 1 http://math.mit.edu/[...] Cambridge University Press 2012

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com