골롬 부호화

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 원리
3. 최적 매개변수 선택
- 3.1. 기하 분포에서의 최적 매개변수
- 3.2. 적응적 골롬-라이스 부호화 (Adaptive Run-length Golomb–Rice Encoding)
4. 런 길이 부호화 (Run-Length Encoding)
5. 응용 분야
6. 한국의 관련 기술 및 정책 동향
참조

1. 개요

골롬 부호화는 정수를 몫과 나머지로 나누어 압축하는 엔트로피 부호화 방법이다. 양의 정수 x를 매개변수 M으로 나누어 몫 q는 단항 부호화, 나머지 r은 절단 이진 부호화로 표현하며, M이 2의 거듭제곱일 경우 라이스 부호화와 동일하다. 골롬 부호화는 런 길이 부호화와 결합하여 압축 효율을 높일 수 있으며, 이미지, 오디오, 비디오 압축 등 다양한 분야에서 예측 잔차를 부호화하는 데 사용된다.

2. 원리

골롬 부호화는 조정 가능한 매개변수 M을 사용하여 입력 값 x를 M으로 나눈 몫 q와 나머지 r의 두 부분으로 나눈다. 몫은 단항 부호화로, 나머지는 절단 이진 부호화로 전송된다. M = 1이면 골롬 부호화는 단항 부호화와 동일하다.

골롬-라이스 코드는 숫자를 'bin'(q)의 위치와 'bin' 내의 'offset'(r)으로 나타내는 코드로 생각할 수 있다. 아래 그림은 골롬-라이스 매개변수 M = 3을 사용하여 정수 x를 부호화하는 위치 q와 offset r을 보여주며, 소스 확률은 p(0) = 0.2인 기하 분포를 따른다.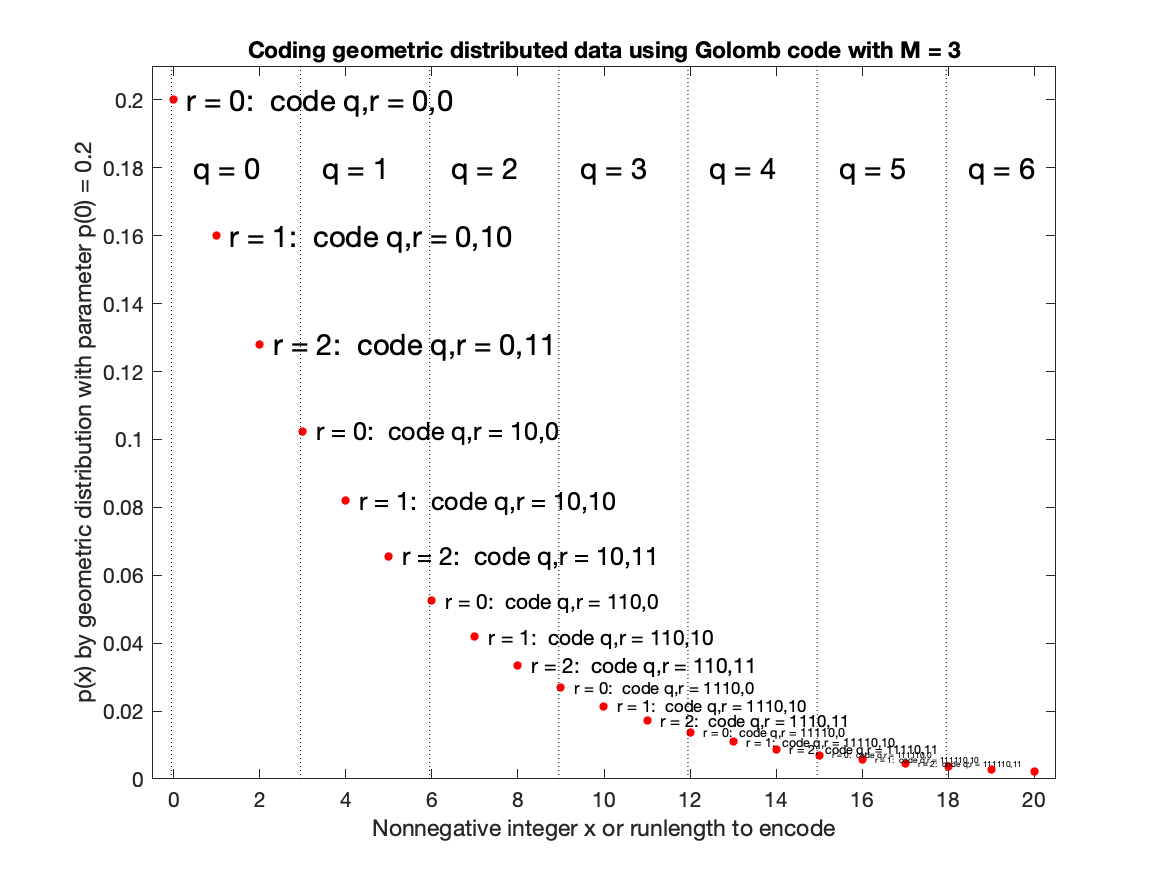

q와 r은 모두 가변 비트 수로 부호화된다. q는 단항 코드로, r은 라이스 코드의 경우 b 비트로, 골롬 코드의 경우 b와 b+1 비트 중에서 선택하여 부호화된다(M이 2의 거듭제곱이 아닌 경우). 여기서

b = \lfloor\log_2(M)\rfloor

이다. 만약

r < 2^{b+1} - M

이면, r을 부호화하기 위해 b 비트를 사용하고, 그렇지 않으면 r을 부호화하기 위해 b+1 비트를 사용한다. M이 2의 거듭제곱이면

b=\log_2(M)

이고, r의 모든 값을 b 비트로 부호화할 수 있다.

골롬은 0부터 시작하는 베르누이 과정의 런 길이를 부호화했으며, 이는 기하 분포를 가진다. 매개변수 M의 최적 선택은

p = P(x=0)

로 매개변수화되는 해당 베르누이 과정의 함수이며, 이는 주어진 베르누이 시행에서 성공 확률이다. M은 분포의 중앙값 또는 중앙값 ±1이다. 이는 다음 부등식으로 결정할 수 있다.

:

(1-p)^M + (1-p)^{M+1} \leq 1 < (1-p)^{M-1} + (1-p)^M,

이것은 다음으로 풀린다.

:

M = \left\lceil -\frac{\log(2 -p)}{\log(1-p)}\right\rceil

.

p(0) = 0.2인 경우,

M = \left\lceil -\frac{\log(1.8)}{\log(0.8)}\right\rceil  = \left\lceil 2.634 \right\rceil = 3

이다.

이 분포에 대한 골롬 코드는 무한한 소스 값 집합에 대해 허프만 코드를 계산할 수 있다면 동일한 확률에 대한 허프만 코드와 동일하다.

M이 최적으로 선택되었을 때, 1 − p(0) ≥ 0.45에 대한 골롬 코드의 비트 단위 중복성.

부호화 파라미터로 1 이상의 정수값 m을 사용한다. m > 1일 때, 부호화 대상 정수값 x (≧ 0)에 대해 x를 m으로 나눈 몫을 q, 나머지를 r이라고 한다.

1. 몫 q를 unary 부호를 사용하여 부호화한다.

2. 나머지 r은

\log_2 m

에 따라 다음과 같이 부호화한다.

$\log_2 m$ 이 정수값이면, 즉 m이 2의 거듭제곱이면 r을 $\log_2m$ 비트의 바이너리 부호로 부호화한다.
그 외의 경우, $b=\lceil\log_2 m\rceil$ 일 때
$r < 2^b-m$ 이면, b - 1 비트로 r을 바이너리 부호화한다.
그 외에는, $r+2^b-m$ 을 b 비트의 바이너리 부호화한다.

m = 1일 때는 unary 부호와 동일하며, m이 2의 거듭제곱(

m=2^k

)일 때는 라이스 부호와 동일하다. 골롬 부호의 원 논문에서는 몫의 부호화에서 일반적인 unary 부호와 0과 1을 반전시키고 있지만, 본질적인 차이는 없다.

m = 3일 때, b = 2,

2^b-m=1

이다. 따라서 r = 0을 1비트로, r = 1, 2를

r+2^b-m

으로 한 다음 2비트로 부호화한다.

m = 3의 경우
수치(x)	몫(q)	나머지(r)	몫의 부호	나머지의 부호	부호(전체)
0	0	0	0	00	000
1	0	1	0	10	010
2	0	2	0	11	011
3	1	0	10	00	1000
4	1	1	10	10	1010
5	1	2	10	11	1011
6	2	0	110	00	11000
7	2	1	110	10	11010

그 외 부호화의 예
x	m = 4	m = 5	m = 8
0	100	100	1000
1	101	101	1001
2	110	110	1010
3	111	1110	1011
4	0100	1111	1100
5	0101	0100	1101
6	0110	0101	1110
7	0111	0110	1111
8	00100	01110	01000
9	00101	01111	01001
10	00110	00100	01010
11	00111	00101	01011
12	000100	00110	01100

2. 1. 부호화 과정

골롬 부호화는 양의 정수 x를 매개변수 M을 사용하여 두 부분으로 나누어 부호화한다. x를 M으로 나눈 몫 q는 단항 부호화로, 나머지 r은 절단 이진 부호화로 표현한다. M = 1이면 골롬 부호화는 단항 부호화와 같다.

몫 q와 나머지 r은 다음과 같이 주어진다.

:

q = \left \lfloor \frac{x}{M} \right \rfloor

:

r = x - qM

q는 단항 코드로 부호화되며, r은 M이 2의 거듭제곱인 경우 b 비트로, 그렇지 않은 경우 b 비트 또는 b+1 비트로 부호화된다. 여기서

b = \lfloor\log_2(M)\rfloor

이다. 만약

r < 2^{b+1} - M

이면 b 비트를 사용하고, 그렇지 않으면 b+1 비트를 사용한다.

예를 들어 M = 10일 때,

b = \lfloor\log_2(10)\rfloor = 3

이고, 컷오프는

2^{b+1} - M = 16 - 10 = 6

이다. 십진수 42를 M = 10인 라이스-골롬 부호화로 표현하면 q = 4, r = 2가 되고, qcode(4),rcode(2) = 11110,010으로 부호화된다.

M = 10일 때 몫 q와 나머지 r의 부호화는 다음과 같다.

{|valign="top"

|

몫 부분 인코딩
q	출력 비트
0	0
1	10
2	110
3	1110
4	11110
5	111110
6	1111110
$\vdots$	$\vdots$
N	$\underbrace{111\cdots111}_N 0$

|

나머지 부분 인코딩
r	오프셋	이진법	출력 비트
0	0	0000	000
1	1	0001	001
2	2	0010	010
3	3	0011	011
4	4	0100	100
5	5	0101	101
6	12	1100	1100
7	13	1101	1101
8	14	1110	1110
9	15	1111	1111

|}

1 이상의 정수값 m을 부호화 파라미터로 사용할 때, 부호화 대상 정수값 x (≧0)에 대해 x를 m으로 나눈 몫을 q, 나머지를 r이라고 한다. 부호화 과정은 다음과 같다.

1. 몫 q는 unary 부호로 부호화한다.

2. 나머지 r은 $\log_2 m$ 에 따라 다음과 같이 부호화한다.

$\log_2 m$ 이 정수이면, 즉 m이 2의 거듭제곱이면 r을 $\log_2m$ 비트의 바이너리 부호로 부호화한다.
그렇지 않으면, $b=\lceil\log_2 m\rceil$ 일 때,
$r < 2^b-m$ 이면, b - 1 비트로 r을 바이너리 부호화한다.
그 외에는, $r+2^b-m$ 을 b 비트의 바이너리 부호화한다.

m = 1일 때는 unary 부호와 같고, m이 2의 거듭제곱(

m=2^k

)일 때는 라이스 부호와 같다.

m = 3일 때, b = 2,

2^b-m=1

이다. 따라서 r = 0을 1비트로, r = 1, 2를

r+2^b-m

으로 한 다음 2비트로 부호화한다.

m = 3의 경우
수치(x)	몫(q)	나머지(r)	몫의 부호	나머지의 부호	부호(전체)
0	0	0	0	00	000
1	0	1	0	10	010
2	0	2	0	11	011
3	1	0	10	00	1000
4	1	1	10	10	1010
5	1	2	10	11	1011
6	2	0	110	00	11000
7	2	1	110	10	11010

그 외 부호화의 예
x	m = 4	m = 5	m = 8
0	100	100	1000
1	101	101	1001
2	110	110	1010
3	111	1110	1011
4	0100	1111	1100
5	0101	0100	1101
6	0110	0101	1110
7	0111	0110	1111
8	00100	01110	01000
9	00101	01111	01001
10	00110	00100	01010
11	00111	00101	01011
12	000100	00110	01100

2. 2. 라이스 부호화

로버트 F. 라이스(Robert F. Rice)가 발명한 라이스 부호화는 골롬 부호의 일종으로, 더 간단한 접두사 코드를 생성한다. 라이스 부호화는 적응 부호화 방식에 사용되거나, 골롬 부호 중 조절 가능한 매개변수가 2의 거듭제곱인 부호를 지칭한다. 이는 2로 곱하거나 나누는 연산이 이진 산술에서 효율적이기 때문에 컴퓨터에서 사용하기 편리하다.

라이스 부호화는 기하 분포가 시간에 따라 변동하거나 정확히 알려져 있지 않은 경우가 많아, 최적의 부호를 선택하는 것이 큰 의미가 없을 수 있다는 점에 착안하여 제안되었다.

라이스 부호화는 여러 무손실 이미지 압축 및 오디오 데이터 압축 방법에서 엔트로피 부호화 단계로 사용된다.

라이스-골롬 부호화에서 나머지 코드는 "라이스 부호화"를 사용한다. 즉, ''M'' 매개변수가 2의 거듭제곱이면 더 간단한 라이스 부호화와 동일해진다.

부호화 및 복호화 과정은 다음과 같다.
부호화 과정1. 정수 값으로 매개변수 ''M''을 고정한다.

2. 부호화할 숫자 ''N''에 대해 몫 ''q''와 나머지 ''r''을 구한다.

몫 = ''q'' = floor(''N''/''M'')
나머지 = ''r'' = ''N'' modulo ''M''

3. 부호어를 생성한다.

코드 형식: <몫 코드><나머지 코드>
몫 코드(단항 부호화)
''q'' 길이의 1 비트 문자열을 작성하고, 0 비트를 작성한다.
나머지 코드(절단 이진 부호화)
$b = \lfloor\log_2(M)\rfloor$
만약 $r < 2^{b+1}-M$ 이면, ''r''을 ''b'' 비트를 사용하여 이진 표현으로 부호화한다.
만약 $r \ge 2^{b+1}-M$ 이면, 숫자 $r+2^{b+1}-M$ 을 ''b'' + 1 비트를 사용하여 이진 표현으로 부호화한다.

복호화 과정1. ''q''의 단항 표현을 디코딩한다(코드 시작 부분의 1의 개수를 센다).

2. 0 구분 기호를 건너뛴다.

3.

b = \lfloor\log_2(M)\rfloor

다음 ''b'' 비트를 이진수 ''r'''로 해석한다. 만약 $r' < 2^{b+1}-M$ 이면, 나머지는 $r = r'$ 이다.
그렇지 않으면 ''b + 1'' 비트를 이진수 ''r'''로 해석하고, 나머지는 $r = r' - 2^{b+1} + M$ 이다.

4.

N = q * M + r

을 계산한다.
추가 설명부호화의 파라미터로 1 이상의 정수값 m을 사용한다. m > 1일 때, 부호화 대상 정수값 x (≧0)에 대해, x를 m으로 나눈 몫을 q, 나머지를 r이라고 한다.

몫 q를 unary 부호를 사용하여 부호화한다.
나머지 r은 $\log_2 m$ 에 따라 다음과 같이 부호화한다.
$\log_2 m$ 이 정수값이다. 즉, m이 2의 거듭제곱일 경우, r을 $\log_2m$ 비트의 바이너리 부호로 부호화한다.
그 외의 경우, $b=\lceil\log_2 m\rceil$ 이라고 할 때
$r < 2^b-m$ 이면, b - 1 비트로 r을 바이너리 부호화
그 외에는, $r+2^b-m$ 을 b 비트의 바이너리 부호화

m = 1일 때는 unary 부호와 동일해진다. 또한, m이 2의 거듭제곱일 때(

m=2^k

)는 라이스 부호와 동일해진다.

골롬 부호의 원 논문에서는 몫의 부호화에서 일반적인 unary 부호와 0과 1을 반전시키고 있지만, 본질적인 차이는 없다.

2. 3. 음수 부호화

골롬 부호는 기본적으로 음수가 아닌 정수를 부호화하도록 설계되었다. 그러나 겹침 및 인터리브 방식을 사용하면 음수를 포함하는 정수도 부호화할 수 있다. 이 방식은 모든 값을 고유하고 되돌릴 수 있는 방식으로 양의 정수에 다시 할당한다. 음수와 양수는 0, -1, 1, -2, 2, -3, 3, -4, 4, ... 와 같이 번갈아 나타난다.^[2]

''n''번째 음수 값(-''n'')은 ''n''번째 홀수(2''n'' - 1)에 매핑된다.
''m''번째 양수 값(''m'')은 ''m''번째 짝수(2''m'')에 매핑된다.

이를 수학적으로 표현하면 다음과 같다.

양수 값 ''x''는 (''x''′ = 2|''x''| = 2''x'', ''x'' ≥ 0)에 매핑된다.
음수 값 ''y''는 (''y''′ = 2|''y''| - 1 = -2''y'' - 1, ''y'' < 0)에 매핑된다.

이 방식은 최적은 아니지만 단순성을 위해 사용될 수 있다. 양방향 기하 분포에 대한 최적 코드는 분포 매개변수에 따라 이 코드를 포함하여 여러 가지 골롬 부호 변형을 포함한다.^[2]

3. 최적 매개변수 선택

골롬 부호화의 효율성은 매개변수 ''M''의 선택에 따라 달라진다. 주어진 데이터의 확률 분포에 따라 최적의 ''M'' 값이 결정된다.

3. 1. 기하 분포에서의 최적 매개변수

베르누이 과정에서 0이 나올 확률이 ''p''일 때, 최적의 ''M''은 다음 부등식을 만족하는 값이다.^[3]

:

p^M + p^{M+1} \le 1 < p^{M-1} + p^M

또는, 다음 식으로 근사할 수 있다.^[3]

:

M \simeq \frac{-1}{\log_2{p}}

3. 2. 적응적 골롬-라이스 부호화 (Adaptive Run-length Golomb–Rice Encoding)

데이터의 확률 분포를 미리 알 수 없는 경우, 적응적 방법을 사용하여 매개변수를 동적으로 조정할 수 있다. 정수에 대한 확률 분포가 알려져 있지 않으면 골롬-라이스 부호화에 대한 최적의 매개변수를 결정하기 어렵다. 이러한 문제를 해결하기 위해, 다양한 응용 프로그램에서 두 단계 접근 방식을 사용한다. 첫 단계에서는 데이터 블록을 스캔하여 데이터의 확률 밀도 함수(PDF)를 추정한다. 그 후, 추정된 PDF를 바탕으로 골롬-라이스 매개변수를 결정한다. 이 접근 방식의 간소화된 변형은 PDF가 매개변수화된 집합에 속한다고 가정하고, 데이터로부터 PDF 매개변수를 추정한 뒤 최적의 골롬-라이스 매개변수를 계산하는 것이다.

PDF가 알려져 있지 않거나 변화하는 정수 데이터를 효율적으로 부호화하는 또 다른 방법은 역적응 부호화를 사용하는 것이다. RLGR 부호화^[1]는 마지막으로 부호화된 기호에 따라 골롬-라이스 매개변수를 위 또는 아래로 조정하는 간단한 알고리즘을 사용한다. 복호화기는 부호화 매개변수의 변화를 추적하기 위해 동일한 규칙을 따르므로, 부호화된 데이터 외에 추가 정보가 필요하지 않다. 예측 오류나 멀티미디어 코덱의 변환 계수와 같이 다양한 통계를 다루는 일반화된 가우스 PDF를 가정할 때, RLGR 부호화 알고리즘은 이러한 응용 분야에서 매우 잘 작동한다.

4. 런 길이 부호화 (Run-Length Encoding)

두 개의 기호(P, Q)로 구성된 알파벳에서 P의 발생 확률이 ''p'' (''p'' ≥ 1/2)일 때, 0개 이상의 P와 하나의 Q로 구성된 런(run)을 골롬 부호화를 사용하여 압축할 수 있다. 이때 파라미터 ''M''의 최적 설정은 $- \frac{1}{\log_{2}p}$ 에 가장 가까운 정수이다.

''p'' = 1/2이면 ''M'' = 1이 되며, 골롬 부호는 단항 부호와 같아진다. 즉, ''n''개(n ≥ 0)의 P 다음에 Q가 오는 경우, ''n''개의 1 다음에 0이 오는 방식으로 부호화된다.

더 간단한 코드를 사용하려면 골롬-라이스 파라미터 ''b''(골롬 파라미터 $M=2^b$ )를 $- \log_2(-\log_2 p)$ 에 가장 가까운 정수로 지정할 수 있다. 이 파라미터가 항상 최적은 아니지만, 보통 최적의 라이스 파라미터이며 압축 성능은 최적의 골롬 코드와 매우 유사하다.^[3]

확률 ''p''를 가진 P의 시퀀스를 런 길이 부호화하기 위해 ''b'' 비트를 가진 이진 부분을 가진 라이스 코드를 사용한다고 가정하면, 예상 압축률은 다음과 같이 계산된다.

: $\begin{align}\mathbb{E}[\text{압축률}]&= \sum_{k=1}^\infty (\text{k-런의 압축률}) \cdot \mathbb{P}[\text{비트가 }k\text{-런의 일부}] \\&= \sum_{k=1}^\infty \frac{b+1+\lfloor 2^{-b}(k-1) \rfloor}{k} \cdot kp^{k-1} (1-p)^2 \\&= (1-p)^2 \sum_{j=0}^\infty (b+1+j) \cdot \sum_{i=j2^b+1}^{(j+1)2^b} p^{i-1} \\&= (1-p)^2 \sum_{j=0}^\infty (b+1+j) \cdot \left(p^{2^b j} - p^{2^{b} (j+1)}\right) \\&= (1-p) \cdot \left (b + \sum_{m=0}^\infty p^{2^b m} \right ) \\&= (1-p) \cdot \left(b + {\left (1-p^{2^b} \right )}^{-1}\right ) \\\end{align}$

여기서 $\mathbb{P}[\text{비트가 }k\text{-런의 일부}]$ 는 비트가 ''k'' 비트 런(''k''-1개의 P와 하나의 Q)의 일부가 될 확률이고, $(\text{k-런의 압축률})$ 은 해당 런의 압축률이다. 압축은 $1-\mathbb{E}[\text{압축률}]$ 로 표현되기도 하는데, 이는 압축된 비율을 의미한다.

''p'' ≈ 1인 경우, 이 런 길이 부호화 방식은 엔트로피에 매우 근접한 압축률을 보인다. 예를 들어 ''p'' = 0.99일 때 라이스 코드 ''b'' = 6을 사용하면 91.89% 압축률이 나오는데, 이는 엔트로피 한계인 91.92%와 매우 가깝다.

5. 응용 분야

로버트 F. 라이스(Robert F. Rice)가 발명한 라이스 부호화는 골롬 부호의 일종으로, 적응 부호화 방식에 사용되어 컴퓨터에서 편리하게 사용할 수 있다. 라이스 부호화는 매개변수로 2의 거듭제곱을 사용하여 이진 산술에서 효율적인 연산을 할 수 있도록 한다.

라이스 부호화는 무손실 이미지 압축 및 오디오 데이터 압축 과정에서 엔트로피 부호화 단계로 사용된다. 많은 신호 코덱은 예측 잔차에 라이스 코드를 사용하는데, 이는 예측 알고리즘에서 잔차가 양면 기하 분포를 따르는 경향이 있기 때문이다. 라이스 코드는 이러한 분포에 대한 허프만 코드의 근사치를 제공한다.

골롬-라이스 코더는 라이스 알고리즘 기반 ''무손실 이미지 코덱''의 엔트로피 코딩 단계에서 사용된다.

5. 1. 이미지 압축

JPEG-LS는 예측 잔차를 부호화하는 데 라이스-골롬 부호화를 사용한다.^[4]^[5] 이미지, 동영상, 정지 화상, 음성 압축 등에서 예측 부호화의 일부로 사용되며, 예측 값과의 잔차를 엔트로피 부호화한다.

이미지: JPEG-LS, LOCO-I, FELICS, SFALIC

5. 2. 오디오 압축

FLAC^[5], 애플 무손실 오디오(Apple Lossless), MPEG-4 ALS 등 다양한 무손실 오디오 데이터 압축 코덱은 선형 예측 코딩 단계(애플 무손실 오디오에서는 "적응형 FIR 필터"라고 함) 이후 잔차를 부호화하는 데 라이스 부호화를 사용한다. 이러한 예측 알고리즘에서 잔차는 양면 기하 분포를 따르는 경향이 있으며, 작은 잔차가 큰 잔차보다 더 자주 발생한다. 라이스 부호화는 그러한 분포에 대한 허프만 코드를 근사한다.

5. 3. 비디오 압축

H.264는 예측 잔차를 부호화하는 데 골롬 부호화의 일종인 Exp-Golomb 부호화를 사용한다.^[4] 정수 값의 부호화뿐만 아니라 이미지(동영상, 정지 화상)나 음성의 압축에서 사용되는 예측 부호화의 일부로서, 예측 값과의 잔차를 엔트로피 부호화하는 데에도 이용된다.^[5]

5. 4. 기타

마이크로소프트 원격 데스크톱 프로토콜의 [https://msdn.microsoft.com/en-us/library/ff635165.aspx RemoteFX] 구성 요소는 가상 머신의 화면 콘텐츠를 부호화하는 데 적응형 골롬-라이스 부호화(RLGR)를 사용한다.^[4]

6. 한국의 관련 기술 및 정책 동향

(빈 문서)

참조

_[1] 논문 Optimal source codes for geometrically distributed integer alphabets
_[2] 논문 Coding of sources with two-sided geometric distributions and unknown parameters
_[3] 간행물 Selecting the Golomb Parameter in Rice Coding
_[4] 웹사이트 man shorten http://www.etree.org[...] 2008-12-07
_[5] 웹사이트 FLAC - Format overview https://xiph.org/fla[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com