관망

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 관망 해석의 기본 원리
- 2.1. 관망 해석의 조건
- 2.2. 유량과 손실수두의 관계
3. 관망 해석 방법
- 3.1. 하디 크로스 방법 (Hardy Cross Method)
- 3.2. 기타 관망 해석 방법
4. 불확실성을 고려한 관망 해석
- 4.1. 확률론적 관망 해석
- 4.2. 기타 불확실성 해석 방법
참조

1. 개요

관망 해석은 유체역학의 기본 법칙을 기반으로 관로 내 유량 분포를 분석하는 방법이다. 질량 보존 법칙과 에너지 보존 법칙을 만족해야 하며, 폐회로 내 손실 수두 합이 0, 절점 유입·유출 유량 일치, 유량과 수두손실의 함수 관계 유지가 주요 조건이다. 하디 크로스 방법과 같은 반복 계산법이 널리 사용되지만, 대규모 시스템에서는 계산 시간과 수렴성 문제가 발생할 수 있다. 불확실성을 고려한 확률적 방법과 최대 엔트로피 방법, 시뮬레이션된 어닐링, 유전자 알고리즘 등도 활용된다.

더 읽어볼만한 페이지

수리공학 - 우물
우물은 식수와 관개용으로 사용된 지하수 취수 구조물로, 다양한 재료와 기술로 건설되었으며 깊이와 용도에 따라 여러 종류로 나뉘지만, 오염과 고갈 문제, 사회·문화적 기능 약화라는 과제를 안고 있어 지속 가능한 이용을 위한 노력이 필요하다.
수리공학 - 펌프
펌프는 공기나 액체를 흡입하여 토출하는 기계이며, 진공과 고압을 이용해 작동하고, 원심 펌프, 기어 펌프 등 다양한 종류가 있으며, 효율, 양정, 유량 등으로 성능을 평가하여 산업 전반에 사용된다.

관망

2. 관망 해석의 기본 원리

관망 해석은 유체역학의 기본 법칙인 질량 보존 법칙(연속 방정식)과 에너지 보존 법칙을 기반으로 한다. 질량 보존 법칙은 관망의 한 지점(절점)으로 들어오는 물의 양과 나가는 물의 양이 같다는 것을 의미하며, 키르히호프의 제1법칙으로도 알려져 있다. 에너지 보존 법칙은 관망 내에서 물이 흐르면서 발생하는 마찰 손실(수두 손실)이 경로에 관계없이 일정하다는 것을 의미하며, 키르히호프의 제2법칙이라고도 한다.

2. 1. 관망 해석의 조건

관망 해석은 다음 세 가지 조건을 만족해야 한다.^[1]

# 폐회로를 따라 한쪽 방향으로 측정한 손실 수두의 합은 0이어야 한다. 이때 측정 방향과 흐름 방향이 일치한다면 h_L>0, 반대라면 h_L<0으로 나타낸다.

# 한 절점에서 유입 유량과 유출 유량은 같아야 한다. (continuity equation|연속 방정식^영어)

# 각각의 관에 대해 수두손실과 유량은 적당한 함수 관계가 유지되어야 한다.

파이프의 마찰 계수가 얻어지면 (또는 다르시-바이스바흐 방정식과 같은 파이프 마찰 법칙에서 계산되면), 네트워크에서 유량 및 수두 손실을 계산하는 방법을 고려할 수 있다. 일반적으로 각 노드에서의 수두 손실(전위차)은 무시되며, 파이프 사양(길이 및 직경), 파이프 마찰 특성 및 알려진 유량 또는 수두 손실을 고려하여 네트워크에서 정상 상태 흐름에 대한 해를 구한다.

네트워크의 정상 상태 흐름은 다음 두 가지 조건을 충족해야 한다.

# 임의의 접합점에서 접합점으로 들어오는 총 유량은 해당 접합점에서 나가는 총 유량과 같다(질량 보존의 법칙, 또는 연속성 법칙, 또는 키르히호프의 제1법칙).

# 임의의 두 접합점 사이에서 수두 손실은 경로에 관계없이 독립적이다(에너지 보존의 법칙, 또는 키르히호프의 제2법칙). 이는 수학적으로 네트워크의 임의의 폐루프에서 루프 주변의 수두 손실이 0이 되어야 한다는 진술과 같다.

위의 두 조건에 의해 주어진 방정식의 시스템이 닫혀 있으면(미지수의 수 = 방정식의 수), 즉 알려진 유량이 충분하면, "결정론적" 해를 얻을 수 있다.

이러한 네트워크를 해결하기 위한 고전적인 접근 방식은 하디 크로스 방법을 사용하는 것이다.

2. 2. 유량과 손실수두의 관계

Darcy-Weisbach 공식과 관수로의 평균 유속 경험식에 의해 손실수두 h_L과 유량 Q의 관계는 일반적으로 다음과 같다.^[1]

:

h_L = kQ^n

k는 관의 제원에 의해 결정되는 값이고, n은 Darcy-Weisbach 공식과 Manning 공식 사용 시에는 n=2, Hazen-Williams 공식 적용 시에는 n=1.85를 쓴다.^[1]

3. 관망 해석 방법

수도관망 해석은 다수의 사용자에게 물을 공급하는 지방 자치 단체의 수도 시스템에서 중요한 부분이다. 이 복잡한 관망에서 유량과 압력을 계산하기 위해 다양한 해석 방법이 사용된다.

일반적으로 수도 사업자는 전문 소프트웨어를 사용하여 관망 해석 문제를 자동으로 해결한다. 그러나 스프레드시트나 솔버 기능이 있는 그래프 계산기와 같은 간단한 도구를 사용하여 해결할 수 있는 문제도 많다.

관망 해석은 기본적으로 다음 두 가지 조건을 만족해야 한다.

키르히호프의 제1법칙(연속성 법칙, 질량 보존의 법칙): 임의의 접합점에서 들어오는 총 유량은 나가는 총 유량과 같다.
키르히호프의 제2법칙(에너지 보존의 법칙): 임의의 두 접합점 사이에서 수두 손실은 경로에 관계없이 일정하다. 이는 네트워크의 임의의 폐회로에서 루프 주변의 수두 손실 합이 0이 되어야 함을 의미한다.

이러한 조건을 바탕으로, 하디 크로스 방법 등의 해석 방법을 활용하여 관망 내 유량 분포를 계산할 수 있다.

3. 1. 하디 크로스 방법 (Hardy Cross Method)

하디 크로스 방법은 관망 내 유량 분포를 근사적으로 구하기 위해 반복적인 계산을 사용하는 방법이다. 이 방법은 비교적 간단하고 이해하기 쉬워 널리 사용된다.

하디 크로스 방법은 다음 두 가지 조건을 만족해야 한다.

# 임의의 접합점에서 들어오는 총 유량은 나가는 총 유량과 같다(질량 보존의 법칙, 연속성 법칙, 키르히호프의 제1법칙).

# 임의의 두 접합점 사이에서 수두 손실은 경로에 관계없이 독립적이다(에너지 보존의 법칙, 키르히호프의 제2법칙). 이는 네트워크의 임의의 폐루프에서 루프 주변의 수두 손실이 0이 되어야 한다는 것을 의미한다.

하디 크로스 방법은 다음과 같은 절차로 수행된다.

1. '관망 해석의 조건' 1번을 만족하도록 각각의 관에 흐르는 가정 유량 Q'을 정한다.

2. n, k값을 결정한다. 각 관에 대하여, 가정 유량 Q'에 대한 손실수두 h_L' 즉,

kQ'^n, knQ'^{n-1}

을 계산한다.

3. 각각의 폐회로에 대해

\Sigma h_L'(=\Sigma kQ'^n), \Sigma knQ'^{n-1}

을 계산한다.

4. 3번의 결과를 이용하여

\Delta Q

를 구한다. 이 값이 0이 아닌 경우 Q'에

\Delta Q

를 더하거나 빼서 1차 수정 유량을 정한다. 가정 유량의 방향이 시계방향이면 보정유량을 더해주고, 반시계방향이라면 보정유량을 빼주면 1차 수정 유량을 구할 수 있다. 2개 회로 모두에 속하는 관에 대해서는 이중으로 보정해준다.

5. 다시 2번 과정으로 돌아가서

\Delta Q

가 어느 정도 허용한도 내에 들어올 때까지 계산을 반복한다.

여기서,

$\Delta Q = -\frac{\Sigma kQ'^n}{\Sigma knQ'^{n-1}}$
Q'은 실제 유량 Q에 대한 가정 유량이다. $(Q=Q' + \Delta Q)$
n은 헤이젠-윌리엄스의 경우 1.85이고, 다르시-바이스바흐의 경우 2이다.

시계 방향 지정자(c)는 루프에서 시계 방향으로 이동하는 흐름만을 의미하고, 시계 반대 방향 지정자(cc)는 시계 반대 방향으로 이동하는 흐름만을 의미한다.

초기 추측이 이루어진 후, 두 번째 조건을 평가할 수 있도록 루프를 고려한다. 시작 노드가 주어지면, 시계 방향으로 루프를 돌면서 작업한다. Q가 루프와 동일한 방향이면 각 파이프에 대해 다르시-바이스바흐 방정식에 따라 수두 손실을 더하고, 흐름이 반대 방향이면 수두 손실을 뺀다. 즉, 루프 방향으로 루프 주변의 수두 손실을 더한다. 흐름이 루프와 함께 또는 루프에 반대하는지에 따라 일부 파이프는 수두 손실이 발생하고 일부는 수두 이득(음수 손실)이 발생한다.

키르히호프의 제2법칙(2)을 만족시키기 위해 정상 상태 해에서 각 루프에 대해 0으로 끝나야 한다. 수두 손실의 실제 합이 0과 같지 않으면, 다음 공식에 의해 주어진 양만큼 루프의 모든 흐름을 조정한다. 여기서 양의 조정은 시계 방향이다.

:

\Delta Q = - \frac{ \sum{\scriptstyle\text{head loss}_c} - \sum{\scriptstyle\text{head loss}_{cc}}}{n \cdot (\sum\frac{\text{head loss}_c}{Q_c} + \sum\frac{\text{head loss}_{cc}}{Q_{cc}})},

이 조정은 문제를 해결하지 못한다. 대부분의 네트워크에는 여러 루프가 있기 때문이다. 그러나 이 조정을 사용하는 것은 괜찮다. 흐름 변경이 조건 1을 변경하지 않으므로 다른 루프는 여전히 조건 1을 충족한다. 그러나 다른 루프로 진행하기 전에 첫 번째 루프의 결과를 사용해야 한다.

현대적인 방법은 위의 키르히호프 법칙(접합점 및 수두 손실 기준)에서 일련의 조건을 만드는 것이다. 그런 다음, 모든 방정식을 만족하는 ''Q'' 값을 찾기 위해 근 찾기 알고리즘을 사용한다. 문자 그대로의 마찰 손실 방정식은 ''Q''²라는 용어를 사용하지만, 방향의 변경을 유지하고 싶다. 각 루프에 대해 수두 손실을 더하는 별도의 방정식을 만드십시오. 그러나 ''Q''를 제곱하는 대신, |''Q''|·''Q''를 대신 사용한다(|''Q''|는 ''Q''의 절대값) 공식에 대해, 모든 부호 변경이 결과 수두 손실 계산에 적절하게 반영되도록 한다.

3. 2. 기타 관망 해석 방법

파이프의 마찰 계수를 얻거나 다르시-바이스바흐 방정식과 같은 파이프 마찰 법칙에서 계산하면, 네트워크에서 유량 및 수두 손실을 계산하는 방법을 고려할 수 있다. 일반적으로 각 노드에서의 수두 손실(전위차)은 무시되며, 파이프 사양(길이 및 직경), 파이프 마찰 특성 및 알려진 유량 또는 수두 손실을 고려하여 네트워크에서 정상 상태 흐름에 대한 해를 구한다.

네트워크의 정상 상태 흐름은 다음 두 가지 조건을 충족해야 한다.

1. 임의의 접합점에서 접합점으로 들어오는 총 유량은 해당 접합점에서 나가는 총 유량과 같다(질량 보존의 법칙, 또는 연속성 법칙, 또는 키르히호프의 제1법칙).

2. 임의의 두 접합점 사이에서 수두 손실은 경로에 관계없이 독립적이다(에너지 보존의 법칙, 또는 키르히호프의 제2법칙). 이는 수학적으로 네트워크의 임의의 폐루프에서 루프 주변의 수두 손실이 0이 되어야 한다는 진술과 같다.

(1)과 (2)에 의해 주어진 방정식의 시스템이 닫혀 있고(미지수의 수 = 방정식의 수), 알려진 유량이 충분하면, "결정론적" 해를 얻을 수 있다.

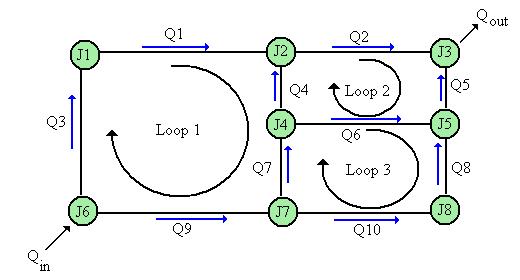
이러한 네트워크를 해결하기 위한 고전적인 접근 방식은 하디 크로스 방법을 사용하는 것이다. 이 공식에서는 먼저 네트워크의 흐름에 대한 추측 값을 생성한다. 흐름은 체적 유량 Q를 통해 표현된다. Q 값에 대한 초기 추측은 키르히호프 법칙(1)을 충족해야 한다. 즉, Q7이 접합점에 들어가고 Q6과 Q4가 동일한 접합점을 나가면 초기 추측은 Q7 = Q6 + Q4를 충족해야 한다. 초기 추측이 이루어진 후, 두 번째 조건을 평가할 수 있도록 루프를 고려한다. 시작 노드가 주어지면, 루프 1에 의해 설명된 것처럼 시계 방향으로 루프를 돌면서 작업한다. Q1과 같이 Q가 루프와 동일한 방향이면 각 파이프에 대해 다르시-바이스바흐 방정식에 따라 수두 손실을 더하고, Q4와 같이 흐름이 반대 방향이면 수두 손실을 뺀다. 즉, 루프 방향으로 루프 주변의 수두 손실을 더한다. 흐름이 루프와 함께 또는 루프에 반대하는지에 따라 일부 파이프는 수두 손실이 발생하고 일부는 수두 이득(음수 손실)이 발생한다.

키르히호프의 제2법칙(2)을 만족시키기 위해 정상 상태 해에서 각 루프에 대해 0으로 끝나야 한다. 수두 손실의 실제 합이 0과 같지 않으면, 다음 공식에 의해 주어진 양만큼 루프의 모든 흐름을 조정한다. 여기서 양의 조정은 시계 방향이다.

:

\Delta Q = - \frac{\sum{\scriptstyle\text{head loss}_c} - \sum{\scriptstyle\text{head loss}_{cc}}}{n \cdot (\sum\frac{\text{head loss}_c}{Q_c} + \sum\frac{\text{head loss}_{cc}}{Q_{cc}})},

여기서

''n''은 헤이젠-윌리엄스의 경우 1.85이고
''n''은 다르시-바이스바흐의 경우 2이다.

시계 방향 지정자(c)는 루프에서 시계 방향으로 이동하는 흐름만을 의미하고, 시계 반대 방향 지정자(cc)는 시계 반대 방향으로 이동하는 흐름만을 의미한다.

이 조정은 문제를 해결하지 못한다. 대부분의 네트워크에는 여러 루프가 있기 때문이다. 그러나 이 조정을 사용하는 것은 괜찮다. 흐름 변경이 조건 1을 변경하지 않으므로 다른 루프는 여전히 조건 1을 충족한다. 그러나 다른 루프로 진행하기 전에 첫 번째 루프의 결과를 사용해야 한다.

하디 크로스 계획에서 '가상 루프'를 사용하여 쌍으로 연결된 네트워크에 연결된 물 저장소를 설명하기 위해 이 방법의 변형이 필요하다. 이에 대한 자세한 내용은 하디 크로스 방법 사이트에서 논의된다.

현대적인 방법은 위의 키르히호프 법칙(접합점 및 수두 손실 기준)에서 일련의 조건을 만드는 것이다. 그런 다음, 모든 방정식을 만족하는 ''Q'' 값을 찾기 위해 근 찾기 알고리즘을 사용한다. 문자 그대로의 마찰 손실 방정식은 ''Q''²라는 용어를 사용하지만, 방향의 변경을 유지하고 싶다. 각 루프에 대해 수두 손실을 더하는 별도의 방정식을 만든다. 그러나 ''Q''를 제곱하는 대신, |''Q''|·''Q''를 대신 사용한다(|''Q''|는 ''Q''의 절대값) 공식에 대해, 모든 부호 변경이 결과 수두 손실 계산에 적절하게 반영되도록 한다.

4. 불확실성을 고려한 관망 해석

실제 수도관망에서는 관 노후화, 유량 변동, 수요 예측 오차 등 다양한 불확실성 요인이 존재하며, 이는 관망 해석에 영향을 미친다.

4. 1. 확률론적 관망 해석

수많은 상황, 특히 수천에서 수백만 개의 노드로 확장될 수 있는 도시의 실제적인 수도관망에서, 결정론적 해를 얻기 위해 필요한 알려진 변수(유량 및/또는 수두 손실)의 수는 매우 크다. 이러한 변수 중 많은 수가 알려져 있지 않거나, 사양에 상당한 불확실성이 수반될 것이다. 또한 많은 관망에서 각 파이프의 평균 유량에 대한 변동으로 설명할 수 있는 유량의 상당한 가변성이 있을 수 있다. 위에서 언급한 결정론적 방법은 지식 부족 또는 유량 변동성으로 인한 불확실성을 설명할 수 없다.

이러한 이유로, 최근 제인스(Jaynes)의 최대 엔트로피 방법에 기반한 관망 분석을 위한 확률적 방법이 개발되었다.^[1]^[2] 이 방법에서는 미지 변수에 대해 연속적인 상대 엔트로피 함수가 정의된다. 이 엔트로피는 키르히호프의 법칙, 파이프 마찰 특성 및 지정된 평균 유량 또는 수두 손실을 포함하는 시스템에 대한 제약 조건에 따라 최대화되어 시스템을 설명하는 확률적 진술(확률 밀도 함수)을 제공한다. 이는 관망에서 유량, 수두 손실 또는 기타 관심 변수의 평균값(기대치)을 계산하는 데 사용될 수 있다. 이 분석은 네트워크의 그래프 표현과 관계없이 분석의 일관성을 보장하는 축소된 매개변수 엔트로피 공식을 사용하여 확장되었다.^[3] 파이프 흐름 네트워크 분석을 위한 베이지안 및 최대 엔트로피 확률적 공식의 비교도 제시되었으며, 특정 가정(가우시안 사전)하에서 두 접근 방식이 평균 유량에 대한 동등한 예측으로 이어진다는 것을 보여주었다.^[4]

4. 2. 기타 불확실성 해석 방법

수자원 시스템의 확률적 최적화를 위해 시뮬레이션된 어닐링^[5], 유전자 알고리즘^[6]과 같은 메타 휴리스틱 알고리즘이 활용된다.

참조

_[1] 간행물 Maximum entropy analysis of hydraulic pipe flow networks https://dx.doi.org/1[...] J. Hydraulic Eng ASCE 2016
_[2] 서적 Probability Theory: The Logic of Science Cambridge University Press
_[3] 간행물 Reduced-parameter method for maximum entropy analysis of hydraulic pipe flow networks J. Hydraulic Eng ASCE 2017
_[4] 간행물 Comparison between Bayesian and maximum entropy analyses of flow networks https://dx.doi.org/1[...] Entropy 2017
_[5] 논문 Water Distribution Network Design Optimization: Simulated Annealing Approach https://ascelibrary.[...] 1999
_[6] 논문 Water distribution network optimization using a modified genetic algorithm 1999

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com