등변사다리꼴

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의 및 성질
- 2.1. 성질
  - 2.1.1. 증명 (평행하지 않은 한 쌍의 대변의 길이가 같다)
  - 2.1.2. 증명 (두 대각선의 길이가 같다)
3. 특수한 경우
- 3.1. 자기 교차
4. 각
5. 대각선과 높이
- 5.1. 대각선
- 5.2. 높이
6. 면적
7. 외접원
참조

1. 개요

등변사다리꼴은 사다리꼴의 일종으로, 평행하지 않은 두 변(다리)의 길이가 같은 사각형이다. 등변사다리꼴은 대각선의 길이가 같고, 밑각의 크기가 같으며, 평행변의 중점을 연결하는 선분이 평행변에 수직이라는 특징을 가진다. 또한 마주보는 각의 합이 180도이며, 대각선은 서로를 길이가 같은 선분으로 나눈다. 직사각형과 정사각형은 등변사다리꼴의 특수한 경우로 간주되며, 3변 동일 사다리꼴도 존재한다. 등변사다리꼴의 면적은 밑변과 윗변 길이의 평균에 높이를 곱하여 구할 수 있으며, 외접원의 반지름은 특정 공식을 통해 계산된다.

더 읽어볼만한 페이지

사각형 - 정사각형
정사각형은 네 변의 길이와 네 각의 크기가 같고, 네 내각이 직각이며, 대각선이 서로 수직 이등분하는 사각형이다.
사각형 - 직사각형
네 각이 직각인 사각형인 직사각형은 평행사변형과 사다리꼴의 특수한 형태이며, 대변의 길이가 같고 평행하며 두 대각선이 서로를 이등분하는 특징을 가진다.

등변사다리꼴
개요
축 대칭인 등변사다리꼴
종류	사각형, 사다리꼴
변의 수	4
대칭	Dih1, [], (*), order 1
쌍대	Kite
성질	볼록, 내접사각형

2. 정의 및 성질

등변사다리꼴은 윗변과 아랫변이 평행하고, 평행하지 않은 두 변(다리)의 길이가 같은 사각형이다. 등변사다리꼴은 다음과 같은 성질을 가진다.

대각선의 길이가 같다.
밑각의 크기가 같다.
평행변의 중점을 연결하는 선분이 평행변에 수직이다.
마주보는 각의 합이 180도이며, 이는 등변사다리꼴이 원내접 사각형임을 의미한다.
대각선은 서로를 길이가 쌍으로 같은 선분으로 나눈다.

마름모는 다리의 길이가 같은 사다리꼴의 특수한 경우이지만, 마주보는 변의 중점을 지나는 대칭축이 없기 때문에 등변사다리꼴은 아니다.^[1]

2. 1. 성질

등변사다리꼴은 아래와 같은 성질을 갖는다. 이 중 하나라도 만족하면 다른 사다리꼴과 등변사다리꼴을 구별할 수 있다.^[1]

대각선의 길이가 같다.
밑각의 크기가 같다.
평행변의 중점을 연결하는 선분이 평행변에 수직이다.
마주보는 각의 합이 180도이며, 이는 등변사다리꼴이 원내접 사각형임을 의미한다.
대각선은 서로를 길이가 쌍으로 같은 선분으로 나눈다.

마름모는 다리의 길이가 같은 사다리꼴의 특수한 경우이지만, 마주보는 변의 중점을 지나는 대칭축이 없기 때문에 등변사다리꼴은 아니다.^[1]

2. 1. 1. 증명 (평행하지 않은 한 쌍의 대변의 길이가 같다)

등변사다리꼴 ABCD에서 점 D를 지나고 윗변(AB)에 평행한 직선이 밑변(BC)와 만나는 점을 E라 하면, 동위각의 성질에 의해 ∠B = ∠DEC이고, ∠B = ∠C = ∠DEC 이므로, △DEC는 이등변삼각형이다. 따라서 DE = DC이다. 또한, □ABED는 평행사변형이므로 AB = DE이다. 따라서 AB = DC이다.

2. 1. 2. 증명 (두 대각선의 길이가 같다)

등변사다리꼴 ABCD에서 대각선 AC, DB를 그으면, △ABC와 △DCB에서

$\mathrm{\overline{AB}=\overline{DC}}$
$\mathrm{\angle B=\angle C}$
$\mathrm{\overline{BC}}$ 는 공통

따라서, SAS 합동에 의해

\mathrm{\triangle ABC \equiv \triangle DCB}

이다.

그러므로

\mathrm{\overline{AC}=\overline{DB}}

이다.

3. 특수한 경우

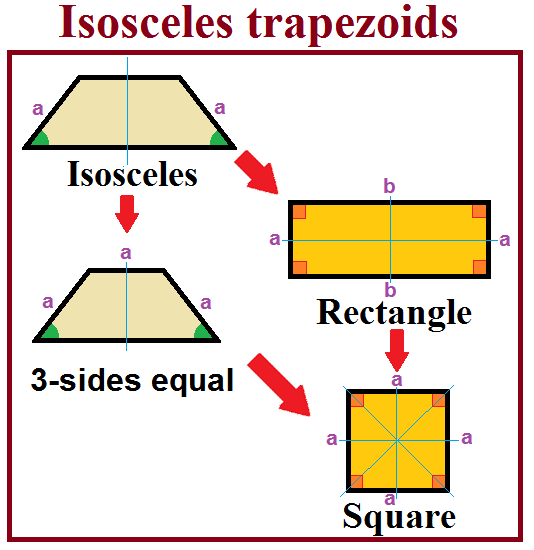
직사각형과 정사각형은 보통 등변사다리꼴의 특수한 경우로 간주되지만, 일부 자료에서는 제외하기도 한다.^[3]

또 다른 특수한 경우는 세 변의 길이가 같은 '''3변 동일 사다리꼴'''이며, '''삼변 사다리꼴'''^[4] 또는 '''삼등변 사다리꼴'''이라고도 불린다. 이는 5개 이상의 변을 가진 정다각형에서 4개의 연속된 꼭짓점을 잘라낸 형태로 볼 수 있다.

3. 1. 자기 교차

자기 교차하지 않고 정확히 하나의 대칭축을 갖는 사각형은 등변사다리꼴 또는 연이어야 한다.^[5] 그러나 교차가 허용되는 경우, 대칭 사각형의 집합은 꼬인 변의 길이가 같고 다른 변이 평행한 꼬인 사각형, 그리고 마주보는 변의 길이가 같은 반평행사변형과 꼬인 등변사다리꼴을 포함하도록 확장되어야 한다.

모든 반평행사변형은 볼록 껍질로 등변사다리꼴을 가지며, 등변사다리꼴의 대각선과 평행하지 않은 변(또는 직사각형의 경우 반대편 변)으로부터 형성될 수 있다.^[6]

볼록 등변사다리꼴	꼬인 등변사다리꼴	반평행사변형

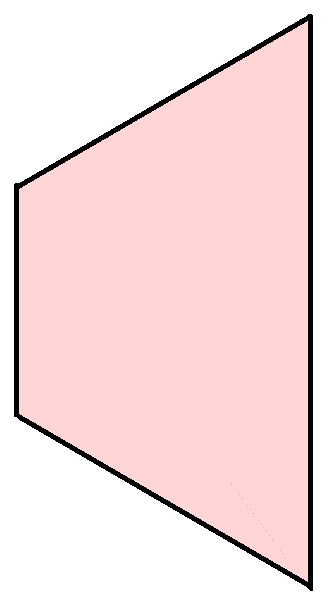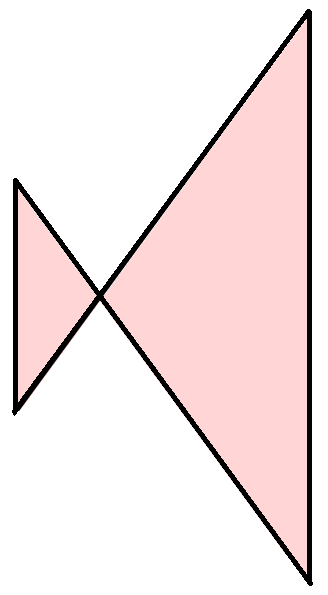4. 각

등변사다리꼴에서 밑각은 쌍으로 같은 크기를 갖는다. --에서, ∠''ABC''와 ∠''DCB''는 같은 크기의 둔각이고, ∠''BAD''와 ∠''CDA''는 같은 크기의 예각이다.

선분 ''AD''와 ''BC''가 평행하므로, 마주보는 밑변에 인접한 각은 보충각 관계에 있으며, 즉 ∠''ABC'' + ∠''BAD'' = 180°이다.

5. 대각선과 높이

등변사다리꼴의 대각선은 길이가 같으며, 서로 같은 비율로 나뉜다. 대각선의 길이는 프톨레마이오스 정리를 통해 구할 수 있다.

피타고라스 정리를 이용하면 등변사다리꼴의 높이를 구할 수 있다.

5. 1. 대각선

등변사다리꼴의 대각선은 길이가 같다. 즉, 모든 등변사다리꼴은 등대각선 사각형이다. 또한, 대각선은 서로 같은 비율로 나뉜다. 그림과 같이 대각선 ''AC''와 ''BD''는 길이가 같고 (''AC'' = ''BD'') 서로 같은 길이의 선분으로 나뉜다 (''AE'' = ''DE'', ''BE'' = ''CE'').

각 대각선이 나뉘는 비율은 그들이 교차하는 평행변의 길이의 비율과 같다. 즉,

:

\frac{AE}{EC} = \frac{DE}{EB} = \frac{AD}{BC}.

각 대각선의 길이는 프톨레마이오스 정리에 따라 다음과 같다.

:

p=\sqrt{ab+c^2}

여기서 ''a''와 ''b''는 평행변 ''AD''와 ''BC''의 길이이고, ''c''는 각 다리 ''AB''와 ''CD''의 길이이다.

5. 2. 높이

피타고라스 정리에 따라, 높이는 다음과 같이 나타낼 수 있다.

:

h=\sqrt{p^2-\left(\frac{a+b}{2}\right)^2}=\tfrac{1}{2}\sqrt{4c^2-(a-b)^2}.

점 ''E''에서 밑변 ''AD''까지의 거리는 다음과 같다.

:

d=\frac{ah}{a+b}

여기서 ''a''와 ''b''는 평행변 ''AD''와 ''BC''의 길이이고, ''h''는 사다리꼴의 높이이다.

6. 면적

등변사다리꼴의 면적은 밑변과 윗변 길이의 평균에 높이를 곱한 값과 같다. 인접한 그림에서 ''AD'' = ''a'', ''BC'' = ''b''로 표기하고, 높이 ''h''가 ''AD''와 ''BC'' 사이의 선분 길이로 이 두 변에 수직이라면, 면적 ''K''는 다음과 같다.

:K = (1/2)(a+b)h

사다리꼴의 높이 대신, 다리의 공통 길이 ''AB'' = ''CD'' = ''c''가 알려져 있다면, 브라마굽타 공식을 사용하여 면적을 계산할 수 있으며, 다음과 같이 단순화된다.

:K = (s-c)√(s-a)(s-b)

여기서 s = (1/2)(a + b + 2c)는 사다리꼴의 반둘레이다. 이 공식은 삼각형의 면적을 계산하는 헤론의 공식과 유사하다. 면적에 대한 이전 공식은 다음과 같이 쓸 수도 있다.

:K = (1/4)√((a-b+2c)(b-a+2c))

7. 외접원

등변사다리꼴의 외접원의 반지름은 다음과 같이 주어진다.^[7]

:R|R^영어 = c)|√()}}}

직사각형에서 ''a'' = ''b''일 경우, 위 식은 R=(1/2)√(a²+c²)|R=(1/2)√(a²+c²) ^영어로 단순화된다.

참조

_[1] 웹사이트 Trapezoid - math word definition - Math Open Reference http://www.mathopenr[...]
_[2] 논문 What is an Isosceles Trapezoid? 1967
_[3] 서적 Big Ideas MATH, Geometry, Texas Edition Big Ideas Learning, LLC (2016) 2016
_[4] 웹사이트 A Hierarchical Classification of Quadrilaterals http://dynamicmathem[...] 2024-02-10
_[5] 서적 Elementary Synthetic Geometry https://books.google[...] J. Wiley & sons 1896
_[6] 서적 The Century Dictionary and Cyclopedia https://books.google[...] The Century co. 1911
_[7] 웹사이트 Trapezoid at Math24.net: Formulas and Tables http://www.math24.ne[...] 2014-07-01

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com