란다우 준위

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 유도와 정의
3. 상대론적 경우
4. 2차원 격자 (호프스태터 나비)
5. 정수 양자 홀 효과
6. 페르미 기체의 자기 감수율
참조

1. 개요

란다우 준위는 균일한 자기장 내에서 전하를 띤 입자의 에너지 양자화 현상을 설명하는 개념이다. 자기장 내에서 전하를 띤 입자는 에너지 준위가 불연속적으로, 즉 란다우 준위로 양자화된다. 란다우 준위는 자기 퍼텐셜, 게이지 고정, 대칭 게이지 등을 사용하여 계산할 수 있으며, 각 란다우 준위는 여러 상태가 겹쳐진 축퇴 상태를 갖는다. 란다우 준위는 상대론적 경우, 2차원 격자, 정수 양자 홀 효과, 페르미 기체의 자기 감수율 등 다양한 물리적 현상과 관련이 있다.

2. 유도와 정의

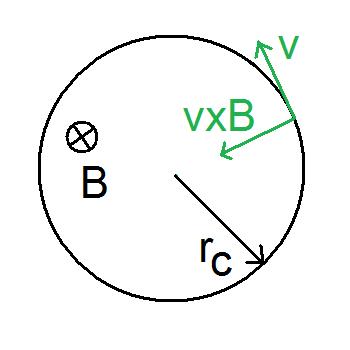
''z''방향으로 균일한 자기장 $\mathbf{B} = B\hat{\mathbf{z}}$ 가 주어진 ''xy'' 평면을 생각하자. 이 자기장에 대한 자기 퍼텐셜 $\mathbf A$ 는

: $\mathbf{A} = xB\hat{\mathbf{y}}$

으로 잡을 수 있다. ''xy'' 평면에 갇힌, 전하 $q$ 를 가진 입자를 생각하자. 이 입자의 해밀토니언은 다음과 같다.^[2]^[4]

: $H=\frac1{2m}(\mathbf p-q\mathbf A)^2=\frac1{2m}\left(p_x^2+(p_y-qxB)^2\right)$

이 해밀토니언은 ''y''방향 운동량과 가환한다.

: $[H,p_y]=0$

따라서 $p_y$ 를 그 고윳값으로 대체할 수 있다. $p_y$ 의 고윳값을 고정시키면, 이 해밀토니언은 위치 에너지

: $V(x)=(p_y-qxB)^2/2m=\frac1{2m}q^2B^2(x-p_y/qB)^2$

를 가지는, 1차원 공간 위에 존재하는 입자다. 이 퍼텐셜은 포물선 꼴이므로, 이는 1차원 양자 조화 진동자이며, 그 각진동수 $\omega$ 는

: $\omega=qB/m$

다. 따라서, 주어진 $p_y$ 에 대한 에너지 준위는 다음과 같다.

: $E_n=\left(\frac1{2}+n\right)\hbar qB/mc$

이 준위들을 '''란다우 준위'''라고 한다.^[2]

속도 '''v'''를 가진 입자의 사이클로트론 궤도 그림. 여기서 '''v'''는 균일한 자기장 '''B''' 하에서 하전 입자(여기서는 양전하)의 고전적 궤적이다. 란다우 양자화는 균일한 자기장 하에 있는 양자 하전 입자를 나타낸다.

## 란다우 게이지

레프 란다우가 도입한 게이지 고정은 균일한 자기장 내의 하전 입자에 자주 사용된다.^[2] 란다우 게이지에서 자기 퍼텐셜

\mathbf{A}

는 다음과 같다.

:

\mathbf{A} = \begin{pmatrix} 0 \\ B\cdot x \\ 0 \end{pmatrix}

이 게이지에서 해밀토니안은 다음과 같다.

:

\hat{H} = \frac{\hat{p}_x^2}{2m} + \frac{1}{2m} \left(\hat{p}_y - qB\hat{x}\right)^2 + \frac{\hat{p}_z^2}{2m}.

연산자

\hat{p}_y

는 해밀토니안과 교환 가능하므로 고유값

\hbar k_y

로 대체될 수 있다.

\hat{z}

는 해밀토니안에 나타나지 않으므로, z-방향 운동은 자유 운동이다.

사이클로트론 공명 주파수

\omega_c=qB/m

를 이용하면 해밀토니안은 다음과 같이 간단하게 표현된다.

:

\hat{H} = \frac{\hat{p}_x^2}{2m} + \frac{1}{2} m \omega_{\rm c}^2 \left( \hat{x} - \frac{\hbar k_y}{m \omega_{\rm c}} \right)^2 + \frac{\hat{p}_z^2}{2m}.

이는 위치 공간에서 포텐셜의 최솟값이

x_0=\hbar k_y/m\omega_c

만큼 이동한 양자 조화 진동자의 해밀토니안과 같다.

조화 진동자 포텐셜을 변환해도 에너지는 영향을 받지 않으므로, 이 시스템의 에너지는 다음과 같다.^[4]

:

E_n=\hbar\omega_{\rm c}\left(n+\frac{1}{2}\right) + \frac{p_z^2}{2m},\quad n\geq 0.

에너지는 양자수

k_y

에 의존하지 않으므로, 유한한 수의 축퇴가 존재한다. 동일한

n

값을 갖는 각 파동 함수 집합을 '''란다우 준위'''라고 한다.

파동 함수는

y

방향의 운동량 고유 상태와

x

방향으로

x_0

만큼 이동한 조화 진동자 고유 상태

|\phi_n\rangle

의 곱으로 인수 분해된다.

:

\Psi(x,y,z) = e^{i(k_y y+k_z z)} \phi_n(x-x_0)

여기서

k_z = p_z / \hbar

이다. 전자의 상태는 양자수

n

,

k_y

,

k_z

로 특징지어진다.

## 대칭 게이지

''z''방향으로 균일한 자기장

\mathbf B=B\hat{\mathbf z}

가 주어진 ''xy'' 평면에서, 자기 퍼텐셜

\mathbf A

를 대칭 게이지로 선택하면 다음과 같다.

:

\hat{\mathbf{A}} =\frac{1}{2} \mathbf{B}\times \hat{\mathbf{r}} = \frac{1}{2}\begin{pmatrix} -By\\ Bx \\0 \end{pmatrix}.

무차원 길이와 에너지로 표현하면, 해밀토니안은 다음과 같이 표현할 수 있다.

:

\hat{H} = \frac{1}{2} \left[\left(-i\frac{\partial}{\partial x} + \frac{y}{2}\right)^2 + \left(-i \frac{\partial}{\partial y} - \frac{x}{2}\right)^2 \right]

다음 연산자들을 정의하자.

\begin{align}\hat{a} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} + \frac{\partial}{\partial x}\right) -i \left(\frac{y}{2} + \frac{\partial}{\partial y}\right)\right] \\\hat{a}^{\dagger} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} - \frac{\partial}{\partial x}\right) +i \left(\frac{y}{2} - \frac{\partial}{\partial y}\right)\right] \\\hat{b} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} + \frac{\partial}{\partial x}\right) +i \left(\frac{y}{2} + \frac{\partial}{\partial y}\right)\right] \\\hat{b}^{\dagger} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} - \frac{\partial}{\partial x}\right) -i \left(\frac{y}{2} - \frac{\partial}{\partial y}\right)\right]\end{align}

이 연산자들은 다음 교환 관계를 만족한다.

:

[\hat{a}, \hat{a}^{\dagger}] = [\hat{b},\hat{b}^{\dagger}] = 1.

이 연산자들로 표현하면, 해밀토니안은 다음과 같이 쓸 수 있다.

:

\hat{H} = \hbar\omega_{\rm c}\left(\hat{a}^{\dagger}\hat{a} + \frac{1}{2}\right),

여기서

\omega_{\rm c}=qB/m

는 사이클로트론 진동수이다.

란다우 준위 지수

n

은 연산자

\hat{N}=\hat{a}^{\dagger}\hat{a}

의 고윳값이다.

\hat{b}^{\dagger}

의 적용은

n

을 유지하면서 각운동량

m_z

를 1만큼 증가시키는 반면,

\hat{a}^{\dagger}

의 적용은 동시에

n

을 증가시키고

m_z

를 1만큼 감소시킨다. 양자 조화 진동자와의 유추는 해를 제공한다.

:

\hat{H} |n,m_z\rangle = E_n |n,m_z\rangle,

여기서

:

E_n = \hbar\omega_{\rm c}\left(n + \frac{1}{2}\right)

이고

:

|n,m_z\rangle = \frac{(\hat{b}^{\dagger})^{m_z+n}}{\sqrt{(m_z+n)!}} \frac{(\hat{a}^{\dagger})^{n}}{\sqrt{n!}}|0,0\rangle.

위 상태가 다음의 파동 함수에 비례하는 것을 확인할 수 있다.

:

\psi_{n,m_z}(x, y) = \left( \frac{\partial}{\partial w} - \frac{\bar{w}}{4} \right)^n w^{n + m_z} e^{-|w|^2 / 4}

여기서

w = x - i y

이다. 특히, 최저 란다우 준위

n = 0

은 가우시안을 곱한 임의의 해석적 함수로 구성되며,

\psi(x,y) = f(w) e^{-|w|^2/4}

이다.

이 결과는 란다우 게이지에서의 결과와 동등하다.

## 축퇴 (Degeneracy)

''z''방향으로 균일한 자기장

\mathbf B=B\hat{\mathbf z}

가 주어지는 경우, 각 란다우 준위는 여러 개의 상태가 겹쳐져 있는 축퇴 상태를 가진다. 이러한 축퇴는 두 번째 양자수

k_y

에 의해 발생하며,

k_y = \frac{2 \pi N}{L_y}

(N은 정수) 값을 가질 수 있다.

허용되는

N

값은 진동 중심

x_0

가 시스템 내부에 물리적으로 존재해야 한다는 조건(

0\le x_0)에 의해 제한된다. 이는 N 에 대한 다음 범위를 제공한다.

:

0 \leq N < \frac{m \omega_{\rm c} L_x L_y}{2\pi\hbar}

.

전하

q=Ze

를 갖는 입자의 경우,

N

의 상한은 자기 선속의 비율로 표현 가능하다.

:

\frac{Z B L_x L_y}{(h/e)} = Z\frac{\Phi}{\Phi_0}

여기서

\Phi_0=h/e

는 기본 자기 선속 양자이고,

\Phi=BA

는 시스템을 통과하는 자기 선속(면적

A=L_xL_y

)이다.

따라서 스핀

S

를 갖는 입자의 경우, 란다우 준위당 최대 입자 수

D

는 다음과 같다.

:

D = Z (2S+1) \frac{\Phi}{\Phi_0}

전자의 경우 (

Z= 1

및

S=1/2

)

D= 2\Phi/\Phi_0

가 되어, 시스템을 관통하는 각 자기 선속 양자당 두 개의 사용 가능한 상태를 제공한다.

제만 분열을 포함하면 각 란다우 준위는 스핀 업 전자와 스핀 다운 전자에 대해 각각 한 쌍으로 분열된다. 그러면 각 스핀 란다우 준위의 점유율은 플럭스 비율

D=\Phi/\Phi_0

이다.

일반적으로 란다우 준위는 전자 시스템에서 관찰되며, 자기장이 증가함에 따라 점점 더 많은 전자가 주어진 란다우 준위에 맞출 수 있다. 가장 높은 란다우 준위의 점유율은 완전히 채워진 것부터 완전히 빈 것까지 다양하며, 이는 드 하스-판 알펜 효과 및 슈브니코프-드 하스 효과와 같은 다양한 전자적 특성의 진동으로 이어진다.

2. 1. 란다우 게이지

''z''방향으로 균일한 자기장

\mathbf{B} = B\hat{\mathbf{z}}

가 주어지는 ''xy'' 평면에서 전하

q

를 가진 입자를 고려하자. 이 입자의 해밀토니언은 다음과 같다.^[2]^[4]

:

H=\frac1{2m}(\mathbf p-q\mathbf A)^2=\frac1{2m}\left(p_x^2+(p_y-qxB)^2\right)

이 해밀토니언은 ''y''방향 운동량과 가환한다.

:

[H,p_y]=0

p_y

를 그 고윳값으로 대체하고, 고윳값을 고정시키면, 이 해밀토니언은 1차원 양자 조화 진동자와 같으며, 각진동수

\omega

는 다음과 같다.

:

\omega=qB/m

따라서 에너지 준위는 다음과 같다.

:

E_n=\left(\frac1{2}+n\right)\hbar qB/mc

이 준위들을 '''란다우 준위'''라고 한다.^[2]

레프 란다우가 도입한 게이지 고정은 균일한 자기장 내의 하전 입자에 자주 사용된다.^[2] 란다우 게이지에서 자기 퍼텐셜

\mathbf{A}

는 다음과 같다.

:

\mathbf{A} = \begin{pmatrix} 0 \\ B\cdot x \\ 0 \end{pmatrix}

이 게이지에서 해밀토니안은 다음과 같다.

:

\hat{H} = \frac{\hat{p}_x^2}{2m} + \frac{1}{2m} \left(\hat{p}_y - qB\hat{x}\right)^2 + \frac{\hat{p}_z^2}{2m}.

연산자

\hat{p}_y

는 해밀토니안과 교환 가능하므로 고유값

\hbar k_y

로 대체될 수 있다.

\hat{z}

는 해밀토니안에 나타나지 않으므로, z-방향 운동은 자유 운동이다.

사이클로트론 공명 주파수

\omega_c=qB/m

를 이용하면 해밀토니안은 다음과 같이 간단하게 표현된다.

:

\hat{H} = \frac{\hat{p}_x^2}{2m} + \frac{1}{2} m \omega_{\rm c}^2 \left( \hat{x} - \frac{\hbar k_y}{m \omega_{\rm c}} \right)^2 + \frac{\hat{p}_z^2}{2m}.

이는 위치 공간에서 포텐셜의 최솟값이

x_0=\hbar k_y/m\omega_c

만큼 이동한 양자 조화 진동자의 해밀토니안과 같다.

조화 진동자 포텐셜을 변환해도 에너지는 영향을 받지 않으므로, 이 시스템의 에너지는 다음과 같다.^[4]

:

E_n=\hbar\omega_{\rm c}\left(n+\frac{1}{2}\right) + \frac{p_z^2}{2m},\quad n\geq 0.

에너지는 양자수

k_y

에 의존하지 않으므로, 유한한 수의 축퇴가 존재한다. 동일한

n

값을 갖는 각 파동 함수 집합을 '''란다우 준위'''라고 한다.

파동 함수는

y

방향의 운동량 고유 상태와

x

방향으로

x_0

만큼 이동한 조화 진동자 고유 상태

|\phi_n\rangle

의 곱으로 인수 분해된다.

:

\Psi(x,y,z) = e^{i(k_y y+k_z z)} \phi_n(x-x_0)

여기서

k_z = p_z / \hbar

이다. 전자의 상태는 양자수

n

,

k_y

,

k_z

로 특징지어진다.

2. 2. 대칭 게이지

''z''방향으로 균일한 자기장

\mathbf B=B\hat{\mathbf z}

가 주어진 ''xy'' 평면에서, 자기 퍼텐셜

\mathbf A

를 대칭 게이지로 선택하면 다음과 같다.

:

\hat{\mathbf{A}} =\frac{1}{2} \mathbf{B}\times \hat{\mathbf{r}} = \frac{1}{2}\begin{pmatrix} -By\\ Bx \\0 \end{pmatrix}.

무차원 길이와 에너지로 표현하면, 해밀토니안은 다음과 같이 표현할 수 있다.

:

\hat{H} = \frac{1}{2} \left[\left(-i\frac{\partial}{\partial x} + \frac{y}{2}\right)^2 + \left(-i \frac{\partial}{\partial y} - \frac{x}{2}\right)^2 \right]

다음 연산자들을 정의하자.

\begin{align}\hat{a} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} + \frac{\partial}{\partial x}\right) -i \left(\frac{y}{2} + \frac{\partial}{\partial y}\right)\right] \\\hat{a}^{\dagger} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} - \frac{\partial}{\partial x}\right) +i \left(\frac{y}{2} - \frac{\partial}{\partial y}\right)\right] \\\hat{b} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} + \frac{\partial}{\partial x}\right) +i \left(\frac{y}{2} + \frac{\partial}{\partial y}\right)\right] \\\hat{b}^{\dagger} &= \frac{1}{\sqrt{2}} \left[\left(\frac{x}{2} - \frac{\partial}{\partial x}\right) -i \left(\frac{y}{2} - \frac{\partial}{\partial y}\right)\right]\end{align}

이 연산자들은 다음 교환 관계를 만족한다.

:

[\hat{a}, \hat{a}^{\dagger}] = [\hat{b},\hat{b}^{\dagger}] = 1.

이 연산자들로 표현하면, 해밀토니안은 다음과 같이 쓸 수 있다.

:

\hat{H} = \hbar\omega_{\rm c}\left(\hat{a}^{\dagger}\hat{a} + \frac{1}{2}\right),

여기서

\omega_{\rm c}=qB/m

는 사이클로트론 진동수이다.

란다우 준위 지수

n

은 연산자

\hat{N}=\hat{a}^{\dagger}\hat{a}

의 고윳값이다.

\hat{b}^{\dagger}

의 적용은

n

을 유지하면서 각운동량

m_z

를 1만큼 증가시키는 반면,

\hat{a}^{\dagger}

의 적용은 동시에

n

을 증가시키고

m_z

를 1만큼 감소시킨다. 양자 조화 진동자와의 유추는 해를 제공한다.

:

\hat{H} |n,m_z\rangle = E_n |n,m_z\rangle,

여기서

:

E_n = \hbar\omega_{\rm c}\left(n + \frac{1}{2}\right)

이고

:

|n,m_z\rangle = \frac{(\hat{b}^{\dagger})^{m_z+n}}{\sqrt{(m_z+n)!}} \frac{(\hat{a}^{\dagger})^{n}}{\sqrt{n!}}|0,0\rangle.

위 상태가 다음의 파동 함수에 비례하는 것을 확인할 수 있다.

:

\psi_{n,m_z}(x, y) = \left( \frac{\partial}{\partial w} - \frac{\bar{w}}{4} \right)^n w^{n + m_z} e^{-|w|^2 / 4}

여기서

w = x - i y

이다. 특히, 최저 란다우 준위

n = 0

은 가우시안을 곱한 임의의 해석적 함수로 구성되며,

\psi(x,y) = f(w) e^{-|w|^2/4}

이다.

이 결과는 란다우 게이지에서의 결과와 동등하다.

2. 3. 축퇴 (Degeneracy)

''z''방향으로 균일한 자기장

\mathbf B=B\hat{\mathbf z}

가 주어지는 경우, 각 란다우 준위는 여러 개의 상태가 겹쳐져 있는 축퇴 상태를 가진다. 이러한 축퇴는 두 번째 양자수

k_y

에 의해 발생하며,

k_y = \frac{2 \pi N}{L_y}

(N은 정수) 값을 가질 수 있다.

허용되는

N

값은 진동 중심

x_0

가 시스템 내부에 물리적으로 존재해야 한다는 조건(

0\le x_0)에 의해 제한된다. 이는 N 에 대한 다음 범위를 제공한다.

:

0 \leq N < \frac{m \omega_{\rm c} L_x L_y}{2\pi\hbar}

.

전하

q=Ze

를 갖는 입자의 경우,

N

의 상한은 자기 선속의 비율로 표현 가능하다.

:

\frac{Z B L_x L_y}{(h/e)} = Z\frac{\Phi}{\Phi_0}

여기서

\Phi_0=h/e

는 기본 자기 선속 양자이고,

\Phi=BA

는 시스템을 통과하는 자기 선속(면적

A=L_xL_y

)이다.

따라서 스핀

S

를 갖는 입자의 경우, 란다우 준위당 최대 입자 수

D

는 다음과 같다.

:

D = Z (2S+1) \frac{\Phi}{\Phi_0}

전자의 경우 (

Z= 1

및

S=1/2

)

D= 2\Phi/\Phi_0

가 되어, 시스템을 관통하는 각 자기 선속 양자당 두 개의 사용 가능한 상태를 제공한다.

제만 분열을 포함하면 각 란다우 준위는 스핀 업 전자와 스핀 다운 전자에 대해 각각 한 쌍으로 분열된다. 그러면 각 스핀 란다우 준위의 점유율은 플럭스 비율

D=\Phi/\Phi_0

이다.

일반적으로 란다우 준위는 전자 시스템에서 관찰되며, 자기장이 증가함에 따라 점점 더 많은 전자가 주어진 란다우 준위에 맞출 수 있다. 가장 높은 란다우 준위의 점유율은 완전히 채워진 것부터 완전히 빈 것까지 다양하며, 이는 드 하스-판 알펜 효과 및 슈브니코프-드 하스 효과와 같은 다양한 전자적 특성의 진동으로 이어진다.

3. 상대론적 경우

상수 자기장 하에서 디랙 방정식을 따르는 전자는 해석적으로 풀 수 있다.^[6]^[7] 에너지는 다음과 같이 주어진다.

:''E''_rel = ±√(''mc''²)² + (''cħk_z'')² + 2νħω_c''mc''²

여기서 ''c''는 광속이고, 부호는 입자-반입자 성분에 따라 다르며, ''ν''는 음이 아닌 정수이다. 스핀으로 인해 ''ν'' = 0에서의 바닥 상태를 제외한 모든 준위는 축퇴된다.

그래핀의 란다우 준위. 그래핀의 전하 운반자는 상대론적 질량이 없는 디랙 입자처럼 동작한다.

질량이 없는 2차원적인 경우는 그래핀과 같은 단층 물질의 디랙 원뿔 근처에서 시뮬레이션할 수 있으며, 이때 고유 에너지는 다음과 같다.^[8]

:''E''_graphene = ±√(2νħeB''v''_F²)

여기서 광속은 물질의 페르미 속도 ''v''_F로 대체되어야 하며, 음의 부호는 전자 구멍에 해당한다.

4. 2차원 격자 (호프스태터 나비)

호프스태터의 나비도 참조

2차원 무한 격자 내 전하 입자의 타이트 결합 에너지 스펙트럼은 자기 유사성 및 프랙탈 구조를 가지는 것으로 알려져 있으며, 이는 호프스태터의 나비에서 증명되었다.^[10] 격자 셀을 통과하는 플럭손과 자기 선속의 정수비에 대해, 큰 정수에 대한 란다우 준위를 얻을 수 있다.

5. 정수 양자 홀 효과

강한 자기장 내 반도체의 에너지 스펙트럼은 정수 지표로 표시될 수 있는 란다우 준위를 형성한다. 또한, 홀 저항 역시 정수 로 표시되는 이산적인 준위를 나타낸다. 이 두 양이 관련되어 있다는 사실은 여러 방법으로 증명될 수 있지만, 가장 쉽게는 Drude 모델을 통해 확인할 수 있다. 홀 전도율은 전자 밀도 에 따라 다음과 같이 나타난다.

: $\rho_{xy}=\frac{B}{n e}.$

저항 평탄부는

: $\rho_{xy}=\frac{2 \pi\hbar }{e^2}\frac{1}{\nu},$

로 주어지므로, 필요한 밀도는 다음과 같다.

: $n=\frac{B }{\Phi_0}\nu,$

이는 란다우 준위를 채우는 데 필요한 밀도와 정확히 일치한다. 각 준위의 큰 축퇴와 함께 서로 다른 란다우 준위 사이의 갭은 저항을 양자화시킨다.

6. 페르미 기체의 자기 감수율

페르미 기체(상호작용하지 않는 페르미온들의 앙상블)는 금속의 열역학적 성질을 이해하는 데 기초가 된다. 1930년 란다우는 페르미 기체의 자기 감수율에 대한 추정치를 도출했는데, 이는 작은 자기장에서는 상수인 란다우 감수율로 알려져 있다.^[9] 란다우는 또한 자기장이 클 때 감수율이 고주파로 진동한다는 것을 알아냈는데, 이 물리적 현상은 드 하스-반 알펜 효과로 알려져 있다.^[9]

참조

_[1] 논문 Diamagnetismus der Metalle Springer Science and Business Media LLC
_[2] 웹사이트 Charge in Magnetic Field https://courses.phys[...] 2023-03-11
_[3] 문서 An equally correct solution in the Landau gauge would be: $\mathbf{A} = \begin{pmatrix} -B y & 0 & 0 \end{pmatrix}^T$ .
_[4] 서적 Quantum mechanics : non-relativistic theory Butterworth Heinemann
_[5] 논문 A new approach to the ground state of quantum Hall systems. Basic principles
_[6] 논문 Das freie Elektron im homogenen Magnetfeld nach der Diracschen Theorie http://link.springer[...] 1928
_[7] 서적 Quantum Electrodynamics: Volume 4 https://books.google[...] Elsevier 2012-12-02
_[8] 논문 Landau quantization of Dirac fermions in graphene and its multilayers 2017
_[9] 서적 Statistical Physics: Volume 5 https://books.google[...] Elsevier 2013-10-22
_[10] 논문 Landau levels, molecular orbitals, and the Hofstadter butterfly in finite systems http://aapt.scitatio[...] 2004-05

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com