링크 (기구)
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
링키지 메커니즘은 링크와 조인트로 구성되어 움직임을 전달하거나 변환하는 데 사용되는 기계 장치이다. 고대부터 연구되었으며, 제임스 와트의 증기 기관, 체비쇼프의 연구 등 산업 혁명 시기에 중요한 발전을 이루었다. 링키지는 링크의 개수와 조인트 종류에 따라 다양하게 분류되며, 가동성은 링크와 조인트 수에 의해 결정된다. 4절 링크는 가장 단순한 형태이며, 분석 및 합성을 위한 다양한 방법이 개발되었다. 링키지 메커니즘은 로봇, 공작 기계, 생체 시스템 등 다양한 분야에서 활용되며, 한국에서도 전통 농기구와 현대 기술 분야에서 중요한 역할을 한다.
더 읽어볼만한 페이지
- 기구학 - 4절 링크
4절 링크는 4개의 링크가 4개의 1자유도 관절로 연결된 기구로, 관절 조합에 따라 다양한 유형이 존재하며, 각 링크는 특정 역할을 수행하고, 그라쇼프 조건은 움직임 특성을 예측하는 데 사용되며, 여러 기계 시스템에 활용되는 기계 공학의 중요한 연구 분야이다. - 기구학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다. - 기계 부속품 - 밸브
밸브는 유체의 흐름을 제어하는 장치로, 다양한 크기와 작동 방식을 가지며, 산업 전반과 일상생활에서 널리 사용된다. - 기계 부속품 - 크랭크축
크랭크축은 내연 기관에서 피스톤의 왕복 운동을 회전 운동으로 바꾸는 핵심 부품으로, 메인 저널, 크랭크 핀, 크랭크 암, 균형추 등으로 구성되어 엔진 성능과 효율에 중요한 역할을 하며, 자동차, 선박, 항공기 등 다양한 기계 장치에 사용된다. - 글로벌세계대백과를 인용한 문서/{{{분류 - 공 (악기)
공은 금속으로 제작된 타악기로, 다양한 문화권에서 의식, 신호, 음악 연주 등에 사용되며, 형태와 용도에 따라 여러 종류로 나뉜다. - 글로벌세계대백과를 인용한 문서/{{{분류 - 국무회의
국무회의는 대한민국 대통령을 의장으로, 예산, 법률안, 외교, 군사 등 국정 현안을 심의하는 중요한 기관이며, 대통령, 국무총리, 국무위원으로 구성되고, 정례회의는 매주 1회, 임시회의는 필요에 따라 소집된다.
| 링크 (기구) | |
|---|---|
| 지도 정보 | |
| 기본 정보 | |
| 유형 | 기계적 장치 |
| 구성 요소 | 링크(link) 조인트(joint) |
| 주요 기능 | 힘 전달 운동 변환 물체 제어 |
| 종류 | |
| 4절 링크 기구 | 크랭크-로커 메커니즘 더블 크랭크 메커니즘 더블 로커 메커니즘 평행 링크 메커니즘 대칭 링크 메커니즘 반대칭 링크 메커니즘 |
| 5절 링크 기구 | 펜타그래프 |
| 6절 링크 기구 | 워트 링크 기구 왓트 병렬 링크 기구 케임브리지 링크 기구 호켄 링크 기구 |
| 응용 분야 | |
| 기계 장치 | 엔진 펌프 로봇 자동차 건설 기계 농업 기계 포장 기계 |
| 정밀 기기 | 측정 장비 광학 기기 의료 기기 |
| 기타 | 예술 작품 장난감 가구 문 |
2. 역사
아르키메데스[3]는 기하학을 지렛대 연구에 적용했으며, 1500년대까지 알렉산드리아의 헤론과 함께 기계 이론의 주요 원천이 되었다. 레오나르도 다 빈치는 기계와 메커니즘에 창의적인 설계를 남겼다.[4]
링키지는 연결되는 링크의 개수와 조인트의 종류에 따라 다양하게 분류된다. 링키지를 구성하는 기본적인 요소는 다음과 같다.[1]
1700년대 중반, 제임스 와트는 증기 기관의 효율을 높이기 위해 와트의 연결 장치를 고안했다. 이는 직선 운동을 생성하는 연결 장치 연구를 촉진했고, J. J. 실베스터는 회전 운동으로부터 정확한 직선을 생성하는 포셀리에 연결 장치에 대한 연구에 영감을 주었다.[5]
A. B. 켐페는 덧셈과 곱셈을 위한 연결 장치를 대수 곡선을 추적하는 시스템으로 조립할 수 있음을 보여주었다.[6] 이는 기하학과 컴퓨터 과학의 융합 연구를 촉진했다.[7][8]
1800년대 후반, F. 로이어, A. B. W. 케네디, L. 부르메스터는 기술 기하학을 사용하여 연결 장치 시스템의 분석과 합성을 공식화했고, P. L. 체비셰프는 연결 장치의 연구와 발명을 위한 해석 기법을 도입했다.[5]
1900년대 중반, 페르디난트 프로이트슈타인과 G. N. 샌더[9]는 디지털 컴퓨터를 사용하여 연결 장치의 컴퓨터 지원 설계를 시작했다. R. E. 카우프만[13][14]은 ''KINSYN''이라는 연결 장치 설계를 위한 대화형 컴퓨터 그래픽 시스템을 만들었다.
현대에는 로봇, 공작 기계, 케이블 구동 및 텐세그리티 시스템, 생물학적 시스템, 단백질 연구 등 다양한 분야에서 링키지 메커니즘이 활용되고 있다.
3. 링키지의 종류 및 구성
일반적으로 링크 메커니즘은 입력을 다른 출력으로 변환할 때, 동작, 속도, 가속도를 변화시키고, 기계적 이득을 제공한다.[1] 링크 메커니즘을 포함한 전달 메커니즘 전반을 다루는 학문을 기구학이라고 한다.[1]
가장 일반적인 링크 메커니즘은 1자유도를 가지며, 입력 동작에 대해 단일 출력 동작을 한다.[1] 대부분의 링크 메커니즘은 2차원이며, 동작이 하나의 평면으로 제한된다. 공간적인(2차원이 아닌) 링크 메커니즘은 설계가 어렵기 때문에 일반적이지 않다.[1]
링크 메커니즘의 자유도(가동도)는 쿠츠바흐-그루블러 방정식(Kutzbach-Gruebler's equation)을 사용하여 계산할 수 있다.[1] 2차원 링크 메커니즘에 대한 단순화된 식은 다음과 같다.
:
:: = 가동도 = 자유도
:: = (지면 링크를 하나 포함한) 링크의 수
:: = 1자유도 동작 부분의 수(핀이나 슬라이더 조인트의 수)
2차원 평면의 더 복잡한 조인트를 포함한 경우의 쿠츠바흐-그루블러 방정식은 다음과 같다.
:
3차원 동작을 하는 공간적인 링크 요소에 대해서는 다음과 같다.
:
::= 가동도(자유도)
::= (지면 링크를 하나 포함한) 링크의 수
::= (접속 방법이나 자유도에 관계없는) 조인트의 수
::= 각 조인트의 자유도
유압식 동작 기계에서는 독립적으로 제어되는 유압 실린더를 세어 자유도를 쉽게 판정할 수 있다.[1]
설계자는 요구되는 출력 동작, 기계적 배율, 속도와 가속도로부터 링크 메커니즘을 설계한다.[1] 요구된 성능을 달성하기 위해 링크 메커니즘의 종류가 선택되어 조정된다.[1] 각 링크는 벡터로 취급되며, 링크가 하나의 루프를 구성하므로 그 벡터들은 연립 방정식으로 취급할 수 있다.[1] 기계적 배율 및 기타 중요한 값도 마찬가지로 취급할 수 있다.[1] 동작의 방정식을 시간에 대해 미분함으로써 구성 요소의 속도와 가속도를 얻을 수 있다.[1]
3. 1. 조인트의 종류
링키지 시스템에서 가장 일반적인 조인트는 다음과 같다.
공간 링크에 사용되는 대부분의 다른 조인트는 회전 및 프리즘 조인트의 조합으로 모델링된다. 예를 들면 다음과 같다.
4. 링키지의 가동성 (Mobility)
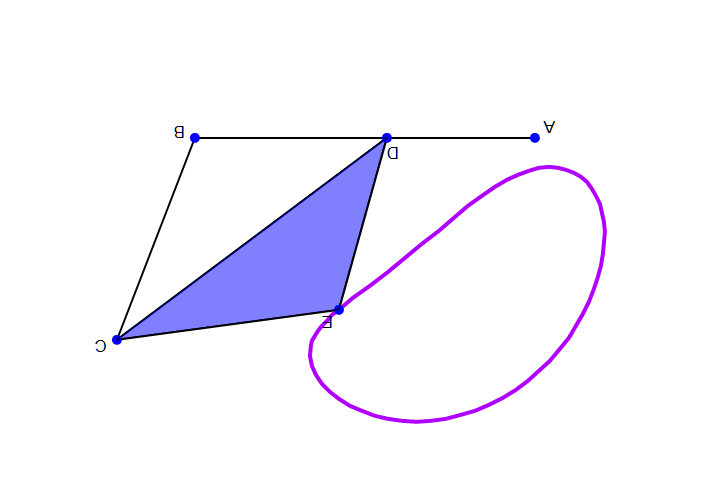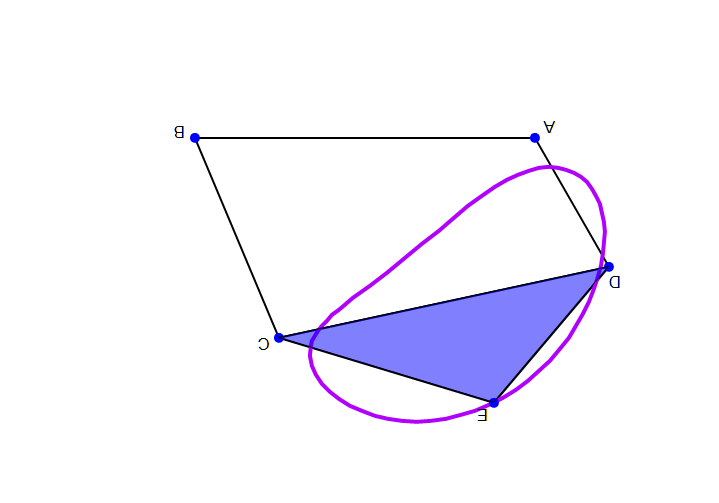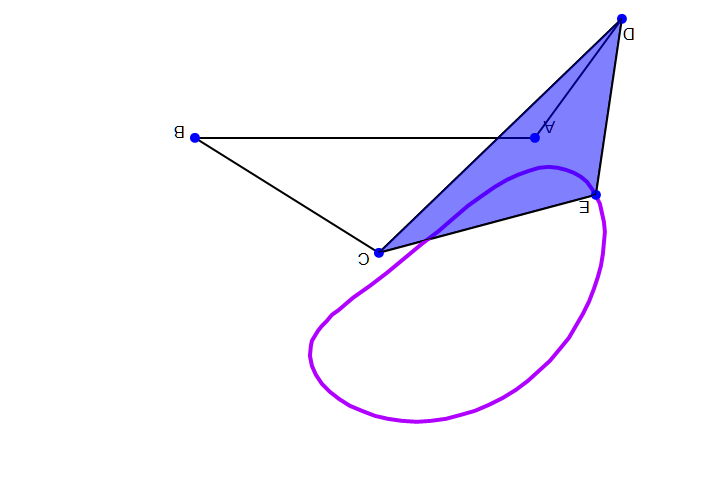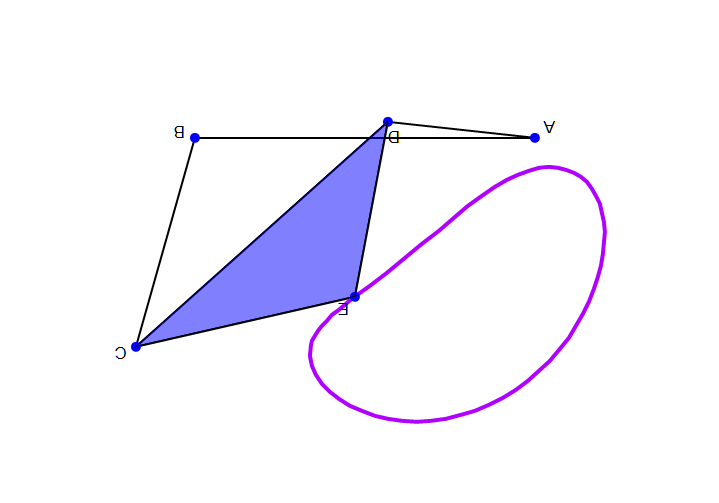
강체 링크들이 이상적인 조인트로 연결된 시스템의 구성은 구성 매개변수 집합으로 정의된다. 예를 들어 회전 조인트 주변의 각도와 인접한 링크 사이에 측정된 프리즈매틱 조인트를 따라 슬라이딩하는 거리 등이 있다. 링크의 기하학적 구속 조건을 통해 모든 구성 매개변수를 최소 집합(입력 매개변수)으로 계산할 수 있다. 입력 매개변수의 수를 링크 시스템의 ''가동성'' 또는 자유도라고 한다.
공간에서 움직이는 ''n''개의 강체 시스템은 고정된 프레임을 기준으로 측정한 6''n''개의 자유도를 갖는다. 이 프레임을 본체 수에 포함하여 가동성이 고정 프레임의 선택과 무관하도록 하면 ''M'' = 6(''N'' − 1)이 되는데, 여기서 ''N'' = ''n'' + 1은 움직이는 본체 수와 고정 본체 수를 합친 것이다.
이 시스템에서 본체를 연결하는 조인트는 자유도를 제거하고 가동성을 감소시킨다. 특히, 힌지와 슬라이더는 각각 5가지 구속 조건을 부과하므로 5개의 자유도를 제거한다. 조인트가 부과하는 구속 조건의 수 ''c''를 조인트의 자유도 ''f''로 정의하는 것이 편리하며, 여기서 ''c'' = 6 − ''f''이다. 1자유도 조인트인 힌지 또는 슬라이더의 경우 ''f'' = 1이므로 ''c'' = 6 − 1 = 5이다.
따라서 ''n''개의 움직이는 링크와 각각 ''f''''i'', ''i'' = 1, ..., ''j'' 자유도를 갖는 ''j''개의 조인트로 구성된 링크 시스템의 가동성은 다음과 같이 계산할 수 있다.
:
여기서 ''N''에는 고정 링크가 포함된다. 이것은 쿠츠바흐-그뤼블러 방정식으로 알려져 있다.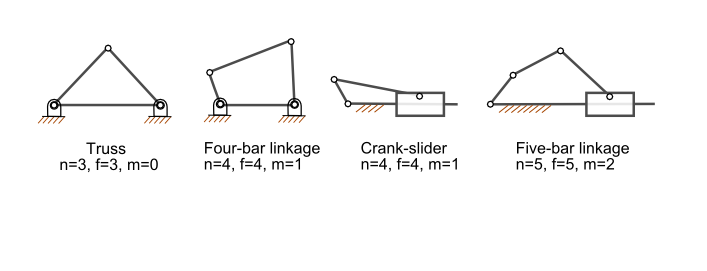

두 가지 중요한 특수한 경우가 있다. (i) 단순 개방형 체인, (ii) 단순 폐쇄형 체인이다. 단순 개방형 체인은 ''j''개의 조인트로 끝에서 끝까지 연결된 ''n''개의 움직이는 링크로 구성되며, 한쪽 끝은 지면 링크에 연결된다. 따라서 이 경우 ''N'' = ''j'' + 1이며 체인의 가동성은 다음과 같다.
::
단순 폐쇄형 체인의 경우 ''n''개의 움직이는 링크가 ''n''+1개의 조인트로 끝에서 끝까지 연결되어 양쪽 끝이 지면 링크에 연결되어 루프를 형성한다. 이 경우 ''N''=''j''이며 체인의 가동성은 다음과 같다.
::
단순 개방형 체인의 예로는 직렬 로봇 매니퓰레이터가 있다. 이러한 로봇 시스템은 6개의 1자유도 회전 또는 프리즈매틱 조인트로 연결된 일련의 링크로 구성되므로 시스템은 6개의 자유도를 갖는다.
단순 폐쇄형 체인의 예로는 RSSR(회전-구면-구면-회전) 공간 4절 링크 메커니즘이 있다. 이러한 조인트의 자유도의 합은 8이므로 링크 메커니즘의 가동성은 2이며, 자유도 중 하나는 두 S 조인트를 연결하는 선을 중심으로 한 커플러의 회전이다.
일반적으로 모든 부품의 움직임이 평행한 평면에 제한되도록 링크 시스템을 설계하여 ''평면 링크''로 알려진 것을 형성하는 것이 일반적이다. 모든 부품이 동심원 구면에서 움직이도록 링크 시스템을 구성하여 ''구면 링크''를 형성하는 것도 가능합니다. 두 경우 모두 링크의 자유도는 6이 아니라 3이 되며, 조인트에 의해 부과되는 구속 조건은 이제 ''c'' = 3 − ''f''이다.
이 경우 가동성 공식은 다음과 같이 주어집니다.
:
그리고 우리는 특수한 경우를 가지고 있다.
- 평면 또는 구면 단순 개방형 체인,
::
- 평면 또는 구면 단순 폐쇄형 체인,
::
평면 단순 폐쇄형 체인의 예로는 평면 4절 링크가 있는데, 이는 4개의 1자유도 조인트가 있는 4절 루프이며 따라서 가동성 ''M'' = 1을 갖는다.
2차원 링크 메커니즘에 대한 단순화된 쿠츠바흐-그루블러 방정식은 다음과 같다.
:
:: = 가동도 = 자유도
:: = (지면 링크를 하나 포함한) 링크의 수
:: = 1자유도 동작 부분의 수(핀이나 슬라이더 조인트의 수)
2차원 평면의 더 복잡한 조인트를 포함한 경우의 쿠츠바흐-그루블러 방정식은 다음과 같다.
:
3차원 동작을 하는 공간적인 링크 요소에 대해서는 다음과 같다.
:
::= 가동도(자유도)
::= (지면 링크를 하나 포함한) 링크의 수
::= (접속 방법이나 자유도에 관계없는) 조인트의 수
::= 각 조인트의 자유도
5. 링키지 메커니즘의 분석 및 합성
링키지 메커니즘의 분석은 시스템의 운동학 방정식을 통해 이루어진다. 이를 통해 입력 매개변수에 따른 시스템의 구성 매개변수를 정의할 수 있다.[1] 프로이트슈타인은 방정식을 사용하여 입력 매개변수와 링키지 구성 간의 특정 관계를 달성하는 평면 4절 링크의 설계 방법을 제시했다.[1] 부르메스터 이론은 평면 4절 링크 설계에 대한 또 다른 접근 방식이다.[1]
6. 평면 1자유도 링키지
평면 링키지의 자유도가 1인 경우, 다음 공식으로 링크와 조인트의 수를 결정할 수 있다.
:
이 공식은 링크가 짝수 개여야 함을 보여준다. 다음은 링크 수(N)와 조인트 수(j)에 따른 링키지의 예시이다.
| 링크 수 (N) | 조인트 수 (j) | 링키지 종류 | 설명 |
|---|---|---|---|
| 2 | 1 | 레버 | |
| 4 | 4 | 사절 링크 | |
| 6 | 7 | 육절 링크 | 3개의 조인트를 갖는 링크 2개(삼차 링크)를 가지며, 연결 방식에 따라 두 가지 토폴로지가 있다. |
| 와트 토폴로지 | 두 개의 삼차 링크가 조인트로 연결된다. | ||
| 스티븐슨 토폴로지 | 두 개의 삼차 링크가 이차 링크로 연결된다.[15] | ||
| 8 | 10 | 8절 링크 | 16가지의 서로 다른 토폴로지가 있다. |
| 10 | 13 | 10절 링크 | 230가지의 서로 다른 토폴로지가 있다. |
| 12 | 16 | 12절 링크 | 6856가지의 서로 다른 토폴로지가 있다. |
14절 및 16절 토폴로지의 수와 자유도가 2, 3, 4인 링크의 수는 Sunkari와 Schmidt를 참조한다.[16]
7. 직선 운동 메커니즘
- 제임스 와트의 병렬 운동 및 와트 기구
- 포셀리에-립킨 기구: 회전 입력으로부터 완벽한 직선 출력을 생성하는 최초의 평면 기구이다. 8절, 1자유도.
- 스콧 러셀 기구: 직선 운동을 입력과 수직인 선에서 (거의) 직선 운동으로 변환한다.
- 체비셰프 기구: 4절 기구로 한 점의 거의 직선 운동을 제공한다.
- 호켄스 기구: 4절 기구로 한 점의 거의 직선 운동을 제공한다.
- 사뤼스 기구: 한 표면의 운동을 다른 표면에 수직인 방향으로 제공한다.
- 하트의 역변환기: 미끄럼 가이드 없이 완벽한 직선 운동을 제공한다.[20]
- 와트의 평행 운동 기구와 Watt's linkage|와트 링크 기구영어
- Peaucellier–Lipkin linkage|포셀리에-립킨 링크 기구영어 - 회전 운동에서 직선 운동을 생성한 최초의 링크 기구. 8링크 1자유도.
- Scott Russell linkage|스콧-러셀 링크 기구영어 - 직선 운동을 입력에 대해 거의 직각 방향의 직선 운동으로 변환한다.
- Chebyshev linkage|체비셰프 링크 기구영어
- Hoeckens linkage|호켄스 링크 기구영어
- 사라스 링크 기구
8. 생체 링키지
링키지 시스템은 동물, 특히 경골어류와 사지동물의 관절에서 널리 발견된다. 대표적인 예로 무릎의 십자인대, 양의 종자골, 조류와 파충류의 두개골 메커니즘 등이 있다.[17] 조류와 파충류의 두개골 메커니즘은 많은 조류에서 위쪽 부리를 위로 움직이는 역할을 한다.
경골어류의 머리에는 연결 메커니즘이 특히 빈번하고 다양하게 나타나는데, 놀래기과와 같이 여러 특수한 섭식 메커니즘을 진화시킨 어류가 여기에 해당한다. 특히 턱 돌출 연결 메커니즘이 발달되었다. 흡입 섭식에서 연결된 4절 링크 시스템은 입의 조정된 개방과 구강의 3차원 확장을 담당한다. 다른 연결계는 돌출 상악골을 담당한다.[17]
링키지는 또한 잠금 메커니즘으로 존재하는데, 말의 무릎과 같이 근육의 능동적인 수축 없이 서서 잠을 잘 수 있게 해준다. 특정 경골어류가 사용하는 피벗 섭식에서는 두 막대의 정렬에 의해 처음에 머리가 배쪽으로 구부러진 위치에 고정되는 4절 링크가 있다. 잠금 메커니즘이 해제되면 머리가 위로 솟아오르고 입이 5~10ms 이내에 먹이를 향해 움직인다.
생물학적 링키지와 공학적 링키지의 중요한 차이점은 생물학에서는 회전 막대가 드물고, 기능적 제약(특히 혈액 공급의 필요성)으로 인해 이론적으로 가능한 범위의 일부만 가능하다는 것이다.[18] 생물학적 링키지는 종종 순응성을 띤다. 종종 하나 이상의 막대는 인대로 형성되며, 링키지는 종종 3차원적이다. 연결된 링키지뿐만 아니라 5, 6, 심지어 7-막대 링키지도 알려져 있지만,[17] 4절 링크가 압도적으로 가장 일반적이다.
9. 응용
링키지 메커니즘은 다양한 분야에서 활용된다.
링크 메커니즘은 원래 기계요소나 공구에 사용되었다. 전형적인 예로는 현가장치와 볼트 커터가 있다. 내연기관의 피스톤, 컨로드, 크랭크는 고전적인 4링크 1자유도 링크 메커니즘이다. 링크 메커니즘은 복잡한 동작을 구현하는 가장 간단하고 저렴하며 효율적인 방법으로 사용되고 있다.
흔히 볼 수 있는 예로는 와이퍼가 있다. 4링크 링크 메커니즘으로 모터의 회전 운동을 진동으로 변환한다. 와이퍼 중에는 링크 메커니즘을 하나 더 갖추어 와이퍼 블레이드를 올바른 방향으로 향하게 하는 것도 있다.[19] 다른 흔한 예로는 4링크 또는 6링크 링크 메커니즘을 광범위하게 사용한 건설 기계가 있다.
3차원 링크 메커니즘은 CAD에 의해 일반적인 것이 되었다.
4링크 링크 메커니즘은 자전거에 사용된다. 일반적인 현가장치를 갖춘 자전거에서는 후륜이 매우 단단한 현처럼 움직여 오르막길에서 힘을 낭비한다. 4링크 링크 메커니즘을 갖춘 자전거에서는 큰 현처럼 바퀴가 움직여 힘의 손실을 약 30퍼센트 줄일 수 있다.
SKELETONICS는 기계적인 링크 메커니즘만으로 작동하는 외골격이다.
10. 한국의 링키지 메커니즘
한국에서는 전통적으로 쟁기, 탈곡기와 같은 농기구와 베틀, 물레와 같은 생활 도구에 링키지 메커니즘이 활용되어 왔다. 근대 이후에는 서양의 기술이 도입되면서 더욱 다양한 링키지 메커니즘이 사용되기 시작했다. 현대에는 자동차, 로봇, 자동화 설비 등 첨단 기술 분야에서 링키지 메커니즘이 핵심적인 역할을 수행하고 있다. 특히, 한국의 로봇 산업은 링키지 메커니즘 기술을 바탕으로 빠르게 성장하고 있으며, 산업용 로봇뿐만 아니라 의료용 로봇, 서비스 로봇 등 다양한 분야에서 활용되고 있다.
참조
[1]
논문
On the Dual-Rod Slider Rocker Mechanism and Its Applications to Tristate Rigid Active Docking
[2]
문서
OED
[3]
논문
From Kinematically Generated Curves to Instantaneous Invariants: Episodes in the History of Instantaneous Planar Kinematics
[4]
서적
A History of Mechanical Inventions
Harvard University Press
[5]
논문
History of the Dynamics of Machines and Mechanisms from Leonardo to Timoshenko
[6]
논문
On a general method of describing plane curves of the nth degree by linkwork
[7]
논문
Configuration Spaces of Mechanical Linkages
[8]
서적
Geometry and Topology of Polygonal Linkages
CRC Press
[9]
논문
Synthesis of Path Generating Mechanisms by Means of a Programmed Digital Computer
[10]
논문
IMP (Integrated Mechanisms Program), A Computer-Aided Design Analysis system for Mechanisms and Linkages
[11]
서적
Kinematics and Mechanism Design
John Wiley
[12]
서적
Robot Manipulators: Mathematics, Programming and Control
MIT Press
[13]
논문
Interactive Linkage Synthesis on a Small Computer
Aug.3–5, 1971
[14]
논문
KINSYN III: A New Human-Engineered System for Interactive Computer-aided Design of Planar Linkages
May
[15]
서적
Mechanism design: enumeration of kinematic structures according to function
https://books.google[...]
CRC Press
2000-09-19
[16]
논문
Structural synthesis of planar kinematic chains by adapting a Mckay-type algorithm
[17]
논문
A novel classification of planar four-bar linkages and its application to the mechanical analysis of animal systems
[18]
뉴스
Why don't animals have wheels?
http://www.simonyi.o[...]
1996-11-24
[19]
서적
Design of Machinery
[20]
웹사이트
True straight-line linkages having a rectlinear translating bar
http://alexandria.tu[...]
[21]
서적
Computer Aided Graphing and Simulation Tools for AutoCAD users
CRC Press
[22]
학회발표
MeKin2D: Suite for Planar Mechanism Kinematics
http://faculty.tamuc[...]
2016-08-21
[23]
논문
A restatement of the optimum synthesis of function generators with planar four-bar and slider-crank mechanisms examples
https://www.research[...]
[24]
웹사이트
PTC Community: Group: Kinematic models in Mathcad
http://communities.p[...]
Communities.ptc.com
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com