맨위로가기

매개변인

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

매개변인은 독립변인과 종속변인 사이의 관계를 설명하는 변수이다. 독립변인이 종속변인에 미치는 영향은 직접효과와 간접효과로 나뉘며, 간접효과를 매개효과라고 한다. 매개효과를 검증하는 방법에는 회귀분석과 구조방정식 모형이 있으며, 조절된 매개와 매개된 조절과 같은 개념도 존재한다. 인과적 매개 분석은 인과 다이어그램과 반사실적 논리에 기반하여 매개효과를 추정하며, 매개 공식은 교란변수가 없는 경우 직접효과와 간접효과를 추정할 수 있는 표현식을 제공한다. 매개효과 분석은 비판과 한계가 존재하며, 적절하게 사용되어야 한다.

더 읽어볼만한 페이지

  • 통계 모형 - 예측 분석
    예측 분석은 통계학, 기계 학습 등의 분석 기법을 활용하여 과거 및 현재 데이터를 토대로 미래의 사건이나 결과를 예측하는 방법론으로, 다양한 분야에서 의사 결정 지원 및 위험 관리 등에 활용되지만, 인간 행동의 복잡성으로 인한 예측 불가능성에 대한 비판도 존재한다.
  • 통계 모형 - 박스-젠킨스 방법
    박스-젠킨스 방법은 자기상관 및 편자기상관 함수를 활용하여 시계열 데이터를 분석하고 예측하는 통계적 방법론으로, ARIMA 모델을 통해 데이터에 적합한 모델을 식별, 추정, 검증한다.
  • 심리측정학 - 재현성
    재현성은 과학적 연구의 신뢰성을 평가하는 요소로, 동일한 조건에서 유사한 결과를 얻을 수 있는 정도를 의미하며, 실험 방법과 데이터의 투명한 공개를 통해 확보해야 한다.
  • 심리측정학 - 조작주의
    조작주의는 과학적 개념을 측정 과정을 통해 정의하는 과학적 실천 방법으로, 물리학에서 시작되어 다양한 분야에서 활용되지만, 경제학에서는 주관적인 개념을 정당화하는 데 사용된다는 비판과 함께 복잡한 사회 현상에 대한 신중한 검토가 필요하다.
매개변인
통계적 모델링
유형통계 모델
관련 항목
관련 항목인과 관계
구조 방정식 모델링
경로 분석
인과 추론
매개효과
정의독립 변수와 종속 변수 사이의 관계를 설명하는 변수
관련 통계 기법회귀 분석
구조 방정식 모델링

2. 매개효과의 개념

매개효과는 독립변수가 종속변수에 직접적인 영향을 주는 것 외에, 매개변수를 통해 간접적으로 영향을 미치는 것을 의미한다.

Baron과 Kenny(1986)는 진정한 매개 관계가 성립하기 위해 충족해야 할 몇 가지 요건을 제시했다.[5] Howell(2009)의 예시를 통해 Baron과 Kenny의 각 단계를 살펴보면 다음과 같다.[6]

# 양육 방식(독립변수)은 자녀 양육에 대한 자신감(종속변수)을 예측한다.

# 양육 방식(독립변수)은 유능함과 자존감(매개변인)을 예측한다.

# 유능함과 자존감(매개변인)은 양육 방식(독립변수)을 통제하면서, 자녀 양육에 대한 자신감(종속변수)을 예측한다.

이러한 결과는 유능함과 자존감에 대한 감정이 양육 방식과 자녀 양육에 대한 자신감 사이의 관계를 매개한다는 결론으로 이어진다.

1단계에서 유의미한 결과가 나오지 않더라도, 2단계로 진행할 근거가 있을 수 있다. 때로는 독립변수와 종속변수 사이에 실제로 유의미한 관계가 있지만, 작은 표본 크기나 다른 외부 요인으로 인해 효과를 예측할 만큼 충분한 검정력이 없을 수 있다.[7]

2. 1. 직접효과와 간접효과

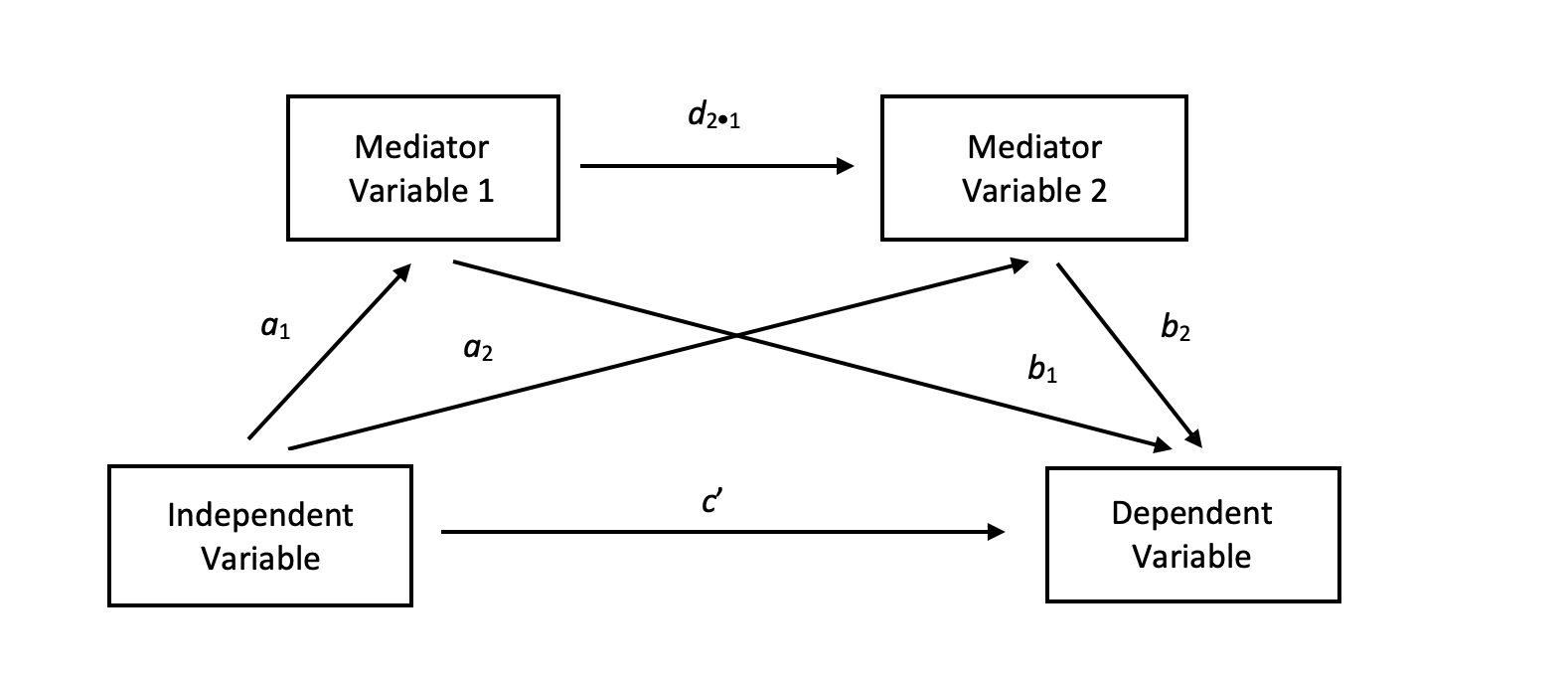
유의한 매개변수가 존재한다면, 독립변인이 종속변인에 주는 영향은 직접효과와 간접효과로 나뉜다. 직접효과(''c'')는 매개변수가 존재함에도 불구하고 매개변수를 거치지 않고 종속변인에 영향을 주는 것이다. 간접효과(''a×b'')는 매개변인을 통해 종속변인에 영향을 주는 것이며, 매개효과라고도 한다. 직접효과와 간접효과를 합한 값을 총효과 또는 전체효과라고 하는데, 이것은 매개변수를 고려하지 않았을 때 독립변인이 종속변인에 주는 영향(''t'')과 같다.[35]

: '''''t''''' '''= ''c'' + ''ab'''''

중재 모형에서의 직접 효과


단순 중재 모형에서의 간접 효과: 간접 효과는 ''X'' 변수가 중재자를 통해 ''Y'' 변수에 미치는 영향의 정도를 나타낸다.


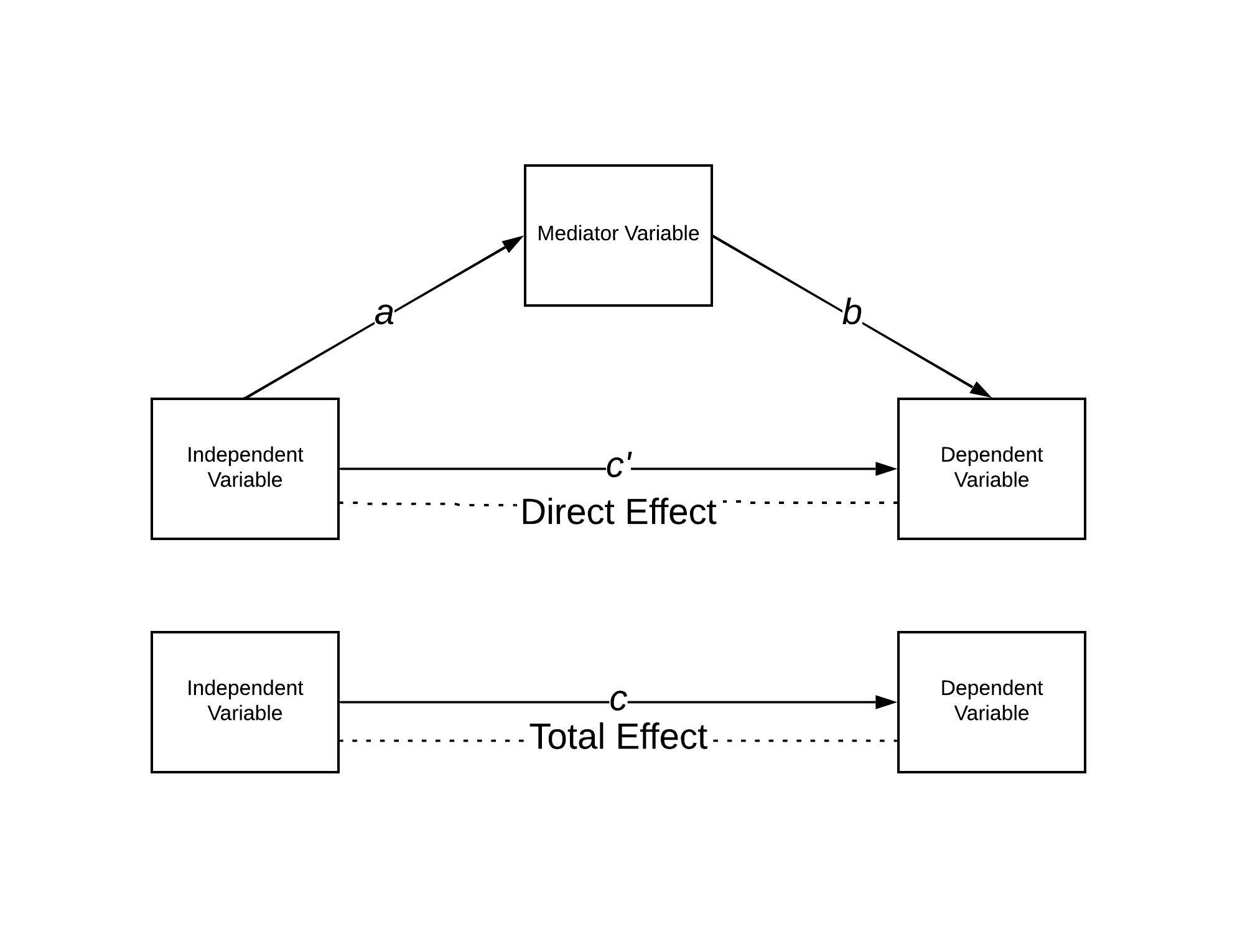
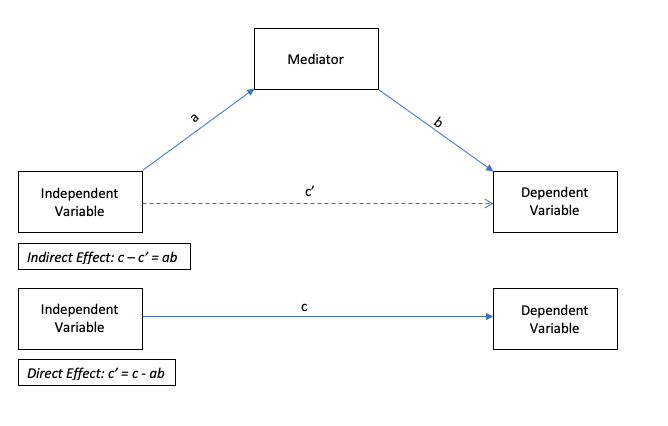
위 그림에서 간접 효과는 경로 계수 "A"와 "B"의 곱이다. 직접 효과는 계수 "C'"이다.

직접 효과는 독립 변수가 1단위 증가하고 중재 변수가 변경되지 않을 때 종속 변수가 얼마나 변하는지를 측정한다. 반대로 간접 효과는 독립 변수가 일정하게 유지되고 중재 변수가 독립 변수가 1단위 증가했을 때 변경되었을 양만큼 변할 때 종속 변수가 얼마나 변하는지를 측정한다.[15][18]

선형 시스템에서 전체 효과는 직접 효과와 간접 효과의 합과 같다(''위 모형에서 C' + AB''). 비선형 모형에서 전체 효과는 일반적으로 직접 효과와 간접 효과의 합과 같지 않고, 둘의 수정된 조합과 같다.[18]

2. 2. 완전매개와 부분매개

매개변수를 추가했을 때 독립변수가 종속변수에 미치는 직접적인 영향(''c'')이 0에 가까워지면 매개효과가 완벽하다고 할 수 있으며, 이를 완전 매개(full mediation)라고 한다.[36][37]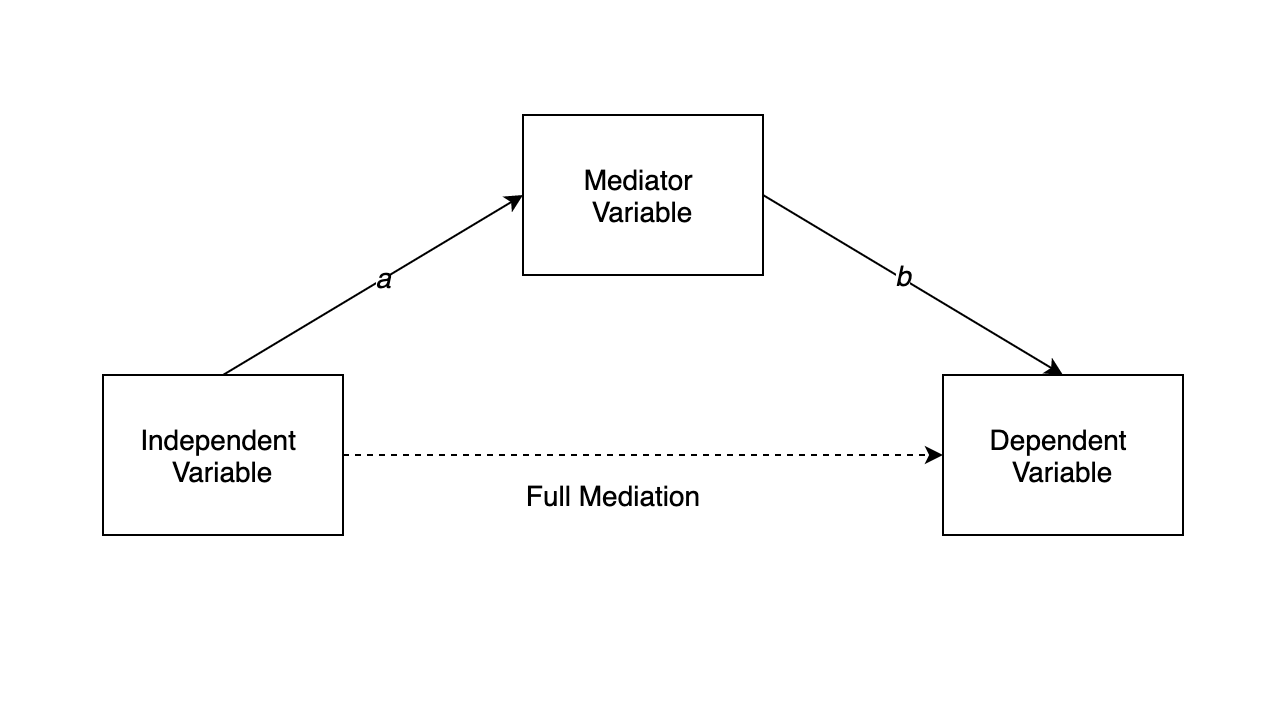
완전 매개 모형


반면, 매개변수를 추가한 후에도 독립변수가 종속변수에 미치는 영향(''c'')이 여전히 통계적으로 유의미하고, 매개변수가 없을 때의 독립변수 효과(''t'')보다 작으면서, 독립변수와 매개변수의 관계(''a'')와 매개변수와 종속변수의 관계(''b'')가 유의하다면, 이를 부분 매개(partial mediation)라고 한다.[36]
부분 매개 모형은 직접 효과를 포함한다.
부분 매개는 매개변수가 독립변수와 종속변수 간 관계의 일부만 설명하고, 독립변수와 종속변수 간의 직접적인 관계도 존재함을 의미한다.

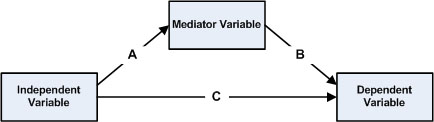
완전 매개 또는 부분 매개를 확인하려면, 독립변수가 설명하는 분산의 감소가 소벨 검정과 같은 검정을 통해 유의미한지 확인해야 한다.[8]

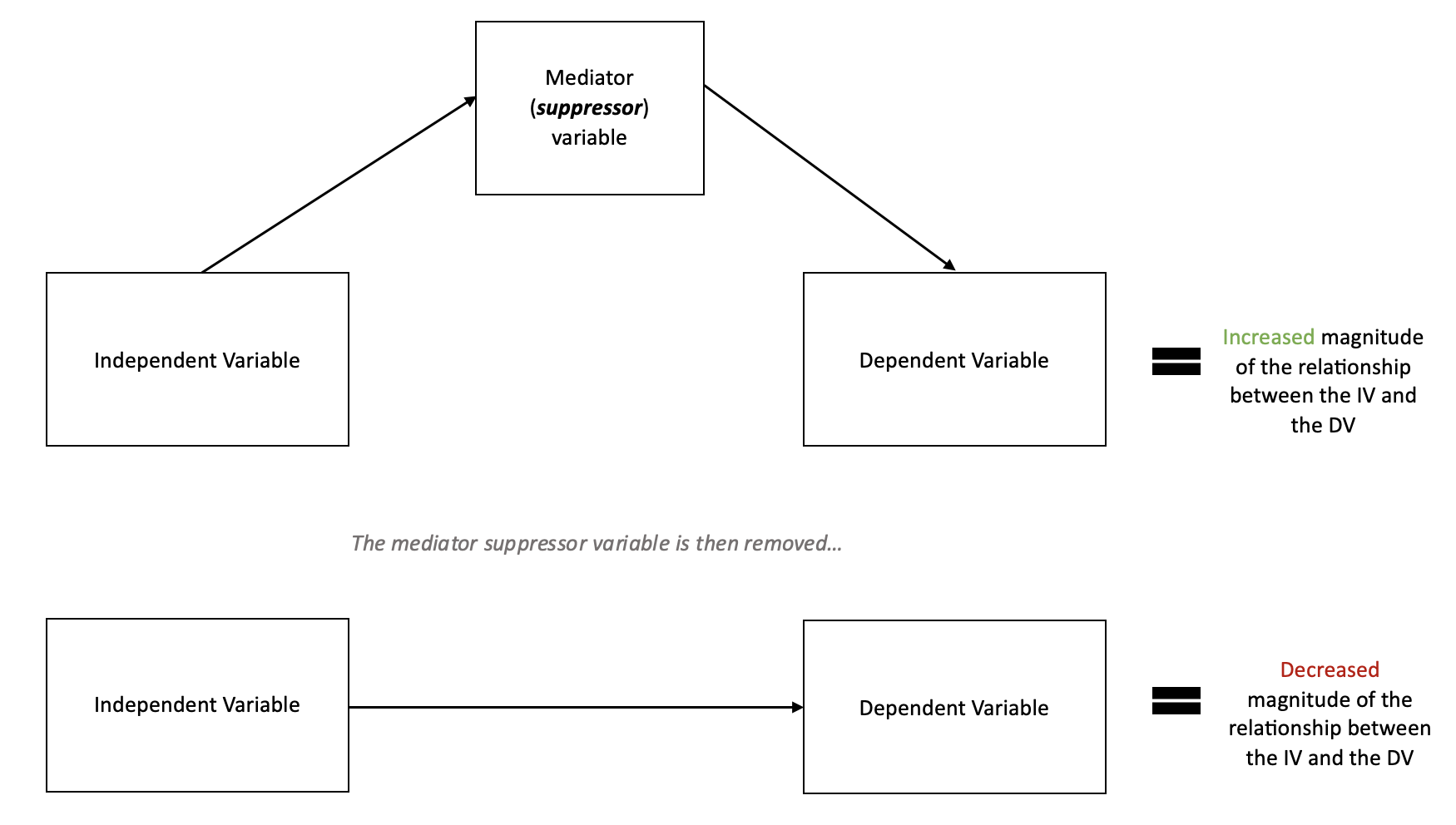
2. 3. 억제효과

억제효과는 특정 변수(억제 변수)가 회귀모형에 포함되지 않았을 때, 다른 변수의 회귀계수가 감소하는 현상이다. 억제 변수를 회귀모형에 포함하면 해당 변수의 회귀계수가 상승하여, 이전에는 발견되지 않았던 효과가 드러나게 된다.[8]

예를 들어, 지능(A)이 높을수록 오류 감지(B)가 증가하여 작업 오류(X)가 감소하는 동시에, 지루함(C)도 증가시켜 작업 오류(X)가 증가하는 상황을 생각해 볼 수 있다. 이때 억제 변수가 없다면 지능은 오류에 영향을 미치지 않거나 약한 영향을 주는 것으로 나타날 수 있다. 그러나 지루함을 통제하면 지능이 오류를 감소시키는 효과가 나타나고, 오류 감지를 통제하면 지능이 오류를 증가시키는 효과가 나타난다. 즉, 지루함만 일정하게 유지하면서 지능을 증가시키면 오류가 감소하고, 오류 감지만 일정하게 유지하면서 지능을 증가시키면 오류가 증가한다.

일반적으로 억제 변수나 교란 변수를 생략하면 변수 간 관계의 크기가 실제보다 감소하거나 인위적으로 증가하게 된다.

다른 변수의 예측 타당성을 증가시키는 조절 변수는 억제 변수로 알려져 있다. 제3의 변수(여기서는 조절 변수)가 추가되면 독립 변수와 종속 변수 간의 관계의 크기가 커진다. 이는 억제를 나타낸다.

3. 매개효과 검증 방법

매개효과를 검증하는 데 널리 쓰이는 방법으로는 회귀분석을 이용하는 방법과 구조방정식 모형(SEM)을 이용하는 방법이 있다.[40] 회귀분석은 매개변인이 측정오차를 가지고 있을 경우, 매개효과를 정확히 검증하지 못할 수 있다. 따라서 매개변인이 측정오차를 포함하고 있을 가능성이 높으면 구조방정식 모형을 이용할 것을 권장한다.

소벨 테스트[8]는 독립 변수와 종속 변수 사이의 관계가 매개 변수의 포함 이후에 유의하게 감소했는지 여부를 확인하는 검사이다. 즉, 이 검사는 매개 효과가 유의미한지 평가한다. 소벨 검정은 독립 변수와 종속 변수 간의 관계를, 매개 변수를 포함한 독립 변수와 종속 변수 간의 관계와 비교하여 검사한다.

소벨 검정은 Baron과 Kenny의 단계보다 더 정확하지만, 통계적 검정력이 낮다. 따라서 유의미한 효과를 감지하려면 큰 표본 크기가 필요하다. 소벨 검정의 주요 가정이 정규성 가정이기 때문에, 작은 표본 크기와 표본 분포의 왜곡은 문제가 될 수 있다. MacKinnon 등 (2002) [10]은 작은 효과를 감지하려면 표본 크기 1000, 중간 효과는 100, 큰 효과는 50이 필요하다고 제안했다.

소벨 테스트 방정식은 다음과 같다.[11]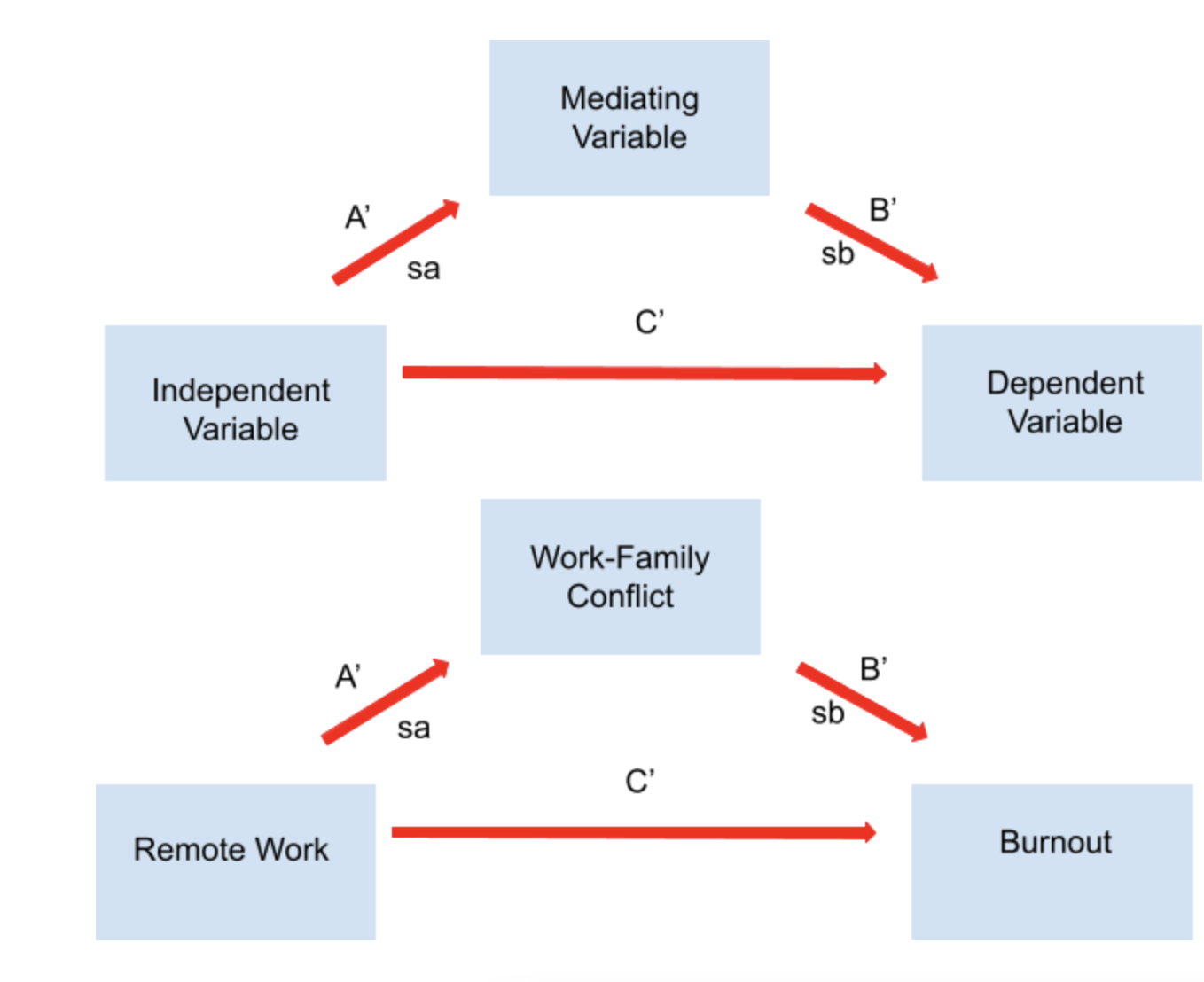

IV가 원격 근무이고 매개 변수가 일-가족 갈등이며 DV가 번아웃인 소벨 테스트. a는 IV와 매개 변수 간의 원시 회귀 계수이고, as는 오류 a의 표준 편차입니다. B는 매개 변수와 DV 간의 원시 계수이고, sb는 b의 표준 오차입니다.


:z= \frac{ab}{\sqrt{b^2s^2_a + a^2s^2_b}}

부트스트래핑[12][13]은 정규성 가정을 충족할 필요가 없고, 작은 표본 크기(''N'' < 25)에서도 효과적으로 사용할 수 있기 때문에 매개효과 검증에 많이 사용된다. 부트스트랩 방법은 비모수 검정이며 정규성 가정을 따르지 않으므로, 원시 데이터가 사용 가능한 경우 권장된다.[11] 부트스트랩은 각 재표본에서 원하는 통계를 계산하기 위해 데이터 집합에서 복원 추출을 통해 관측치를 반복적으로 무작위 표본 추출한다. 수백 또는 수천 번의 부트스트랩 재표본에 걸쳐 계산하면 관심 통계량의 표본 분포를 근사할 수 있다. Preacher–Hayes 방법은 매개효과의 유의미성 또는 비유의미성을 평가할 수 있는 점 추정치와 신뢰 구간을 제공한다. 점 추정치는 부트스트랩 표본 수에 대한 평균이며, 신뢰 구간 사이에 0이 포함되지 않으면 유의미한 매개효과가 있다고 할 수 있다.

Baron과 Kenny[14]의 논리나 소벨 검정을 사용하여 매개효과를 결정하는 것이 일반적이지만, Baron과 Kenny 방법만을 기반으로 하거나 소벨 검정과 같이 분포 가정을 하는 매개효과 검증을 발표하는 것은 점점 더 어려워지고 있다. 따라서 어떤 검정을 수행할지 선택할 때 옵션을 고려하는 것이 중요하다.[9]

3. 1. 회귀분석 이용법

회귀분석을 이용하여 매개변인의 효과를 검증하는 방법은 다음과 같다.[5]

# 독립변인과 종속변인 간의 관계를 나타내는 회귀계수(''t'')의 통계적 유의성을 검증한다.

# 독립변인과 매개변인 간의 관계를 나타내는 회귀계수(''a'')의 통계적 유의성을 검증한다.

# 독립변인과 매개변인을 모두 독립변인으로 간주하여 회귀분석을 실시한 후, 독립변인과 종속변인 간의 관계를 나타내는 회귀계수(''c'')의 유의성을 검증한다.

이때 ''t'', ''a'', ''b'', ''c''는 비표준화계수이다.

Baron과 Kenny (1986)는 매개 관계가 성립하기 위한 몇 가지 조건을 제시했다.

  • 1단계: 독립변수가 종속변수를 유의미하게 예측해야 한다.

:: 독립변수 \to 종속변수

:: Y=\beta_{10} +\beta_{11}X + \varepsilon_1

:: * ''β''11 은 유의미해야 한다.

  • 2단계: 독립변수가 매개변수를 유의미하게 예측해야 한다. 매개변수가 독립변수와 관련이 없다면, 매개효과는 성립할 수 없다.

:: 독립변수 \to 매개변수

:: Me=\beta_{20} +\beta_{21}X + \varepsilon_2

:: * ''β''21이 유의미해야 한다.

  • 3단계: 다중 회귀 분석을 통해 매개변수가 종속변수를 유의미하게 예측하고, 1단계에서 유의미했던 독립변수의 계수(β11)가 감소하거나 유의미하지 않아야 한다.

:: Y=\beta_{30} +\beta_{31}X +\beta_{32}Me + \varepsilon_3

:: * ''β''32는 유의미해야 한다.

:: * ''β''31은 1단계의 β11보다 절댓값이 작아야 한다.

Howell (2009)의 예시를 통해 각 단계를 설명하면 다음과 같다.[6]

# 양육 방식(독립변수)이 자녀 양육 자신감(종속변수)을 예측한다.

# 양육 방식(독립변수)이 유능감과 자존감(매개변수)을 예측한다.

# 유능감과 자존감(매개변수)이 양육 방식(독립변수)을 통제한 상태에서 자녀 양육 자신감(종속변수)을 예측한다.

이러한 결과는 유능감과 자존감이 양육 방식과 자녀 양육 자신감 사이의 관계를 매개한다는 것을 보여준다.

1단계에서 유의미한 결과가 없더라도, 표본 크기가 작거나 다른 외부 요인으로 인해 2단계를 진행할 근거가 있을 수 있다.[7]

3. 2. 구조방정식 이용

구조방정식 모형(SEM)은 측정오차를 고려할 수 있어, 매개변수가 측정오차를 포함하고 있을 가능성이 높을 때 권장된다.[40] 구조방정식을 이용하여 매개변인의 효과를 검증하는 순서는 다음과 같다.

# 매개변인을 포함하지 않은 모형을 구조방정식으로 검증한다.

# 매개변인을 포함한 모형을 구조방정식으로 검증한다.

구조방정식 통계패키지를 이용할 경우에는 간접효과의 t통계량을 확인할 수 있는데, 그 절댓값이 1.96보다 크면 유의수준 5%에서 통계적으로 유의하다.[41]

4. 조절된 매개와 매개된 조절

조절된 매개는 매개와 조절이 통계 모델에서 함께 나타나는 현상이다. 조절된 매개에서는 먼저 매개가 설정된 후, 독립 변수와 종속 변수 간의 관계를 설명하는 매개 효과가 다른 수준의 다른 변수(조절 변수)에 의해 조절되는지 살펴본다. 이는 뮐러(Muller), 저드(Judd), 이저빗(Yzerbyt) (2005)[20] 및 프리처(Preacher), 러커(Rucker), 헤이즈(Hayes) (2007)[21]에 의해 제시되었다.

뮐러, 저드, 이저빗(2005)[20]은 조절된 매개와 매개된 조절의 기반이 되는 세 가지 기본 모형을 설명한다.


  • Mo: 조절 변수
  • Me: 매개 변수
  • εi: 각 회귀 방정식의 측정 오차

  • 전체 조절 효과: 독립 변수(X)와 종속 변수(Y) 사이의 관계(다이어그램에서 경로 ''C'')는 전체 처치 효과라고도 불리며, 조절 변수에 의해 영향을 받는다.
  • Y=\beta_{40} +\beta_{41}X +\beta_{42}Mo +\beta_{43}XMo + \varepsilon_4
  • ''β''43 회귀 가중치가 유의해야 전체 조절 효과가 있으며, 이는 매개된 조절 효과 설정을 위한 첫 번째 단계이다.
  • 조절된 매개를 설정하려면 조절 효과가 없어야 하므로, ''β''43 회귀 가중치는 유의하지 않아야 한다.

  • 독립 변수와 매개 변수 간의 관계 조절 (경로 ''A''):
  • Me=\beta_{50} +\beta_{51}X +\beta_{52}Mo +\beta_{53}XMo + \varepsilon_5
  • ''β''53 회귀 가중치가 유의미하면, 조절 변수가 독립 변수와 매개 변수 간의 관계에 영향을 미친다.

  • 독립 변수와 종속 변수 간의 관계 (경로 ''A'') 및 매개 변수와 종속 변수 간의 관계 (경로 ''B'') 조절:
  • Y=\beta_{60} +\beta_{61}X +\beta_{62}Mo +\beta_{63}XMo +\beta_{64}Me +\beta_{65}MeMo + \varepsilon_6
  • ''β''53 (2단계)과 ''β''63 (3단계)이 모두 유의미하면, 조절 변수는 독립 변수와 매개 변수 간의 관계(경로 ''A'')에 영향을 준다.
  • ''β''53 (2단계)과 ''β65'' (3단계)가 모두 유의미하면, 조절 변수는 매개 변수와 종속 변수 간의 관계(경로 ''B'')에 영향을 미친다.
  • 위의 조건 중 하나 또는 둘 다 해당될 수 있다.

4. 1. 조절된 매개(Moderated mediation)

조절된 매개는 통계 모델에서 매개와 조절이 함께 발생하는 현상이다. 즉, 독립 변수 ''A''가 매개 변수를 거쳐 종속 변수에 미치는 영향(매개 효과)이 다른 변수(조절 변수)의 수준에 따라 달라지는 경우를 의미한다. 본질적으로 조절된 매개에서는 먼저 매개가 설정된 다음, 독립 변수와 종속 변수 간의 관계를 설명하는 매개 효과가 조절 변수에 의해 조절되는지를 조사한다.[20][21]

조절 변수는 독립 변수와 매개 변수 간의 관계(경로 A), 매개 변수와 종속 변수 간의 관계(경로 B), 또는 두 관계 모두를 조절할 수 있다. 조절된 매개 모형에는 다음 그림과 같이 다섯 가지 유형이 있다.[20]

첫 번째 옵션: 독립 변수가 'B' 경로를 조절한다.


두 번째 옵션: 네 번째 변수가 'A' 경로를 조절한다.


세 번째 옵션: 네 번째 변수가 'B' 경로를 조절한다.


네 번째 옵션: 네 번째 변수가 'A' 경로와 'B' 경로를 모두 조절한다.


다섯 번째 옵션: 네 번째 변수가 'A' 경로를 조절하고, 다섯 번째 변수가 'B' 경로를 조절한다.


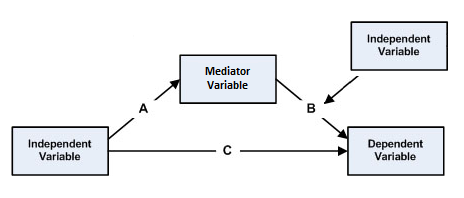
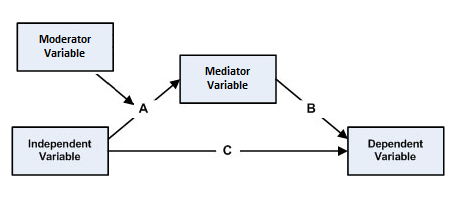
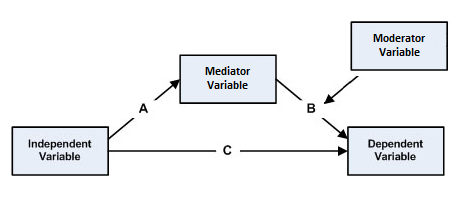
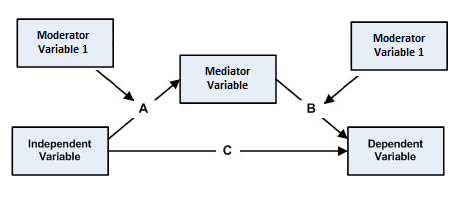
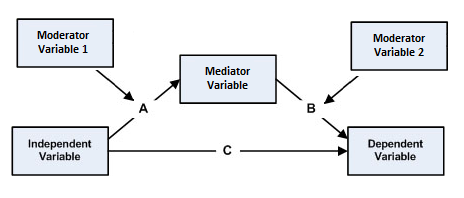
위에 언급된 모델 외에도, 독립 변수와 매개 변수 간의 관계(A 경로)를 조절하는 동시에 새로운 변수가 독립 변수와 종속 변수 간의 관계(C 경로)를 조절하는 경우가 있을 수 있다.[1]

4. 2. 매개된 조절(Mediated moderation)

매개된 조절은 조절 변수와 매개 변수를 모두 포함하는 통계적 개념이다. 이는 독립 변수와 종속 변수 간의 관계에 대한 조절 변수의 영향(조절 효과)이 매개 변수를 통해 전달되는 경우를 의미한다.

매개된 조절을 확인하기 위해서는 먼저 독립 변수와 종속 변수 간의 관계가 조절 변수에 의해 조절되는지 확인해야 한다(조절 효과 검증).[20] 즉, 독립 변수와 종속 변수 간의 관계의 강도나 방향이 조절 변수에 따라 달라지는지 확인한다. 그런 다음, 이러한 조절 효과가 매개 변수를 통해 나타나는지 확인한다.

심리학 연구에서 매개된 조절의 예시를 살펴보자.[22] 참가자들에게 도덕성 또는 힘과 관련된 자극을 제시하고(프라임), 죄수의 딜레마 게임을 진행하게 했다. 연구 결과, 사회적 가치 지향이 친사회적인 사람들은 도덕성/힘 프라임에 영향을 받았지만, 친자신적인 사람들은 그렇지 않았다. 즉, 사회적 가치 지향(조절 변수)은 프라임(독립 변수)과 죄수의 딜레마 게임에서의 행동(종속 변수) 사이의 관계를 조절했다.

더 나아가, 연구자들은 프라임 유형이 참가자의 사회적 가치 지향과 죄수의 딜레마 게임 행동 간의 조절 관계를 매개한다는 것을 발견했다. 도덕성 프라임을 받은 친사회적 참가자는 상대방이 협력할 것이라고 예상하여 자신도 협력했지만, 힘 프라임을 받은 친사회적 참가자는 상대방이 경쟁할 것이라고 예상하여 자신도 경쟁하는 경향을 보였다. 반면, 친자신적 참가자는 항상 경쟁적으로 행동했다.

뮐러, 저드, 이저빗(2005)은 매개된 조절과 조절된 매개의 기반이 되는 세 가지 기본 모형을 제시했다.[20] 여기서 ''Mo''는 조절 변수, ''Me''는 매개 변수를 나타낸다.

  • 전체 조절 효과: 독립 변수(X)와 종속 변수(Y) 간의 관계가 조절 변수(Mo)에 의해 조절되는 경우이다. 수학적으로는 다음과 같이 표현된다.


:Y=\beta_{40} +\beta_{41}X +\beta_{42}Mo +\beta_{43}XMo + \varepsilon_4

여기서 ''β''43이 유의미하면 전체 조절 효과가 존재한다고 본다.

  • 독립 변수와 매개 변수 간 관계 조절: 조절 변수가 독립 변수와 매개 변수 간의 관계(경로 ''A'')에 영향을 미치는 경우이다.

  • 매개 변수와 종속 변수 간 관계 조절: 조절 변수가 매개 변수와 종속 변수 간의 관계(경로 ''B'')에 영향을 미치는 경우이다.


이 두 가지 경우는 다음과 같은 수식으로 표현된다.

:Y=\beta_{60} +\beta_{61}X +\beta_{62}Mo +\beta_{63}XMo +\beta_{64}Me +\beta_{65}MeMo + \varepsilon_6

  • 단계 2에서 ''β''53과 단계 3에서 ''β''63이 모두 유의미하면, 조절 변수는 독립 변수와 매개 변수 간의 관계(경로 ''A'')에 영향을 미친다.
  • 단계 2에서 ''β''53과 단계 3에서 ''β''65가 모두 유의미하면, 조절 변수는 매개 변수와 종속 변수 간의 관계(경로 ''B'')에 영향을 미친다.
  • 위의 조건 중 하나 또는 둘 다 참일 수 있다.

5. 인과적 매개 분석

매개 분석은 전통적으로 선형 회귀를 통해 이루어졌지만, 이는 인과 관계를 명확히 설명하는 데 한계가 있었다.[15][18] 인과 다이어그램과 반사실적 논리에 기반한 현대적 인과 분석 방법은 이러한 한계를 극복하고, 매개효과를 더 정확하게 추정할 수 있게 해준다.

선형 시스템에서 전체 효과는 직접 효과와 간접 효과의 합과 같지만, 비선형 모형에서는 이 둘의 수정된 조합과 같다.[18]

전통적인 매개 분석은 통계적 용어로 인과 관계를 가리는 경향이 있었다. 인과적 접근 방식은 중재자 ''M''을 "통제"하는 것이 항상 적절하지 않다는 점을 강조한다. ''M''을 "통제"하는 것은 물리적으로 ''M''의 변화를 막는 것이 아니라, 단지 같은 ''M'' 값을 가진 경우에만 주목하는 것이다. 확률 이론에는 "''M''의 변화를 막는 것"을 표현할 방법이 없으며, "조건화"만이 가능하다.

예를 들어, ''M''과 ''Y''의 오차항이 상관 관계가 있으면, 구조 계수 ''B''와 ''A''는 ''Y''를 ''X''와 ''M''에 회귀하여 추정할 수 없다.[25] 이 때문에 새로운 추정 전략과 "''M''을 고정하는 것"을 모방하는 연산이 필요하다.

펄(Pearl, 1994)은 ''M''의 방정식을 제거하고 상수 ''m''으로 대체하는 do(''M'' = ''m'') 연산자를 정의했다.[24] 이를 통해 잠재적 결과 또는 구조적 반사실을 얻을 수 있으며, 직접 효과와 간접 효과를 정의하는 데 유용하다.[26][27]

이에 따라 다음과 같은 효과들을 정의할 수 있다.


  • 총 효과 (TE): 중재자가 ''X''의 변화를 따르도록 하면서 ''X''가 0에서 1로 변할 때 ''Y''의 예상 증가
  • 제어된 직접 효과 (CDE): 중재자가 특정 수준 ''m''으로 고정된 상태에서 ''X''가 0에서 1로 변할 때 ''Y''의 예상 증가
  • 자연 직접 효과 (NDE): ''X''가 0에서 1로 변할 때 ''Y''의 예상 증가 (중재 변수는 ''X'' = 0에서 얻었을 값으로 설정)
  • 자연 간접 효과 (NIE): ''X''를 1로 유지하고 ''M''이 ''X'' = 1에서 얻었을 값으로 변할 때 ''Y''의 예상 증가


''TE-NDE''는 중재가 효과를 설명하는 데 얼마나 필요한지를, ''NIE''는 중재가 효과를 유지하는 데 얼마나 충분한지를 측정한다. 간접 효과의 제어된 버전은 변수를 상수로 고정하여 직접 효과를 비활성화할 수 없기 때문에 존재하지 않는다.

총 효과는 다음과 같이 분해할 수 있다.

:TE = NDE - NIE_r

선형 시스템에서는 전환의 역전은 부호 반전을 의미한다. 이러한 정의는 임의의 비선형 상호 작용, 교란 간 종속성, 연속형 및 범주형 변수에 적용 가능하다.

5. 1. 매개 공식(Mediation formula)

매개 공식은 교란변수가 없을 때, 직접효과와 간접효과를 추정할 수 있는 분포 무관(distribution-free) 표현식을 제공한다.[30][31][32] 이를 통해 다양한 상호작용 계수가 매개효과에 어떻게 기여하는지 알 수 있다.[29][30]

선형 분석에서 모든 효과는 구조 계수의 곱의 합으로 결정되며, 다음과 같다.

:

\begin{align}

TE & = C + AB \\

CDE(m) & = NDE = C, \text{ } m에 관계없이\\

NIE & = AB.

\end{align}



따라서 모델이 식별될 때마다 모든 효과를 추정할 수 있다. 비선형 시스템에서는 직접 및 간접 효과를 추정하기 위해 더 엄격한 조건이 필요하다.[18][28][29] 예를 들어, 교란이 존재하지 않는 경우(즉, ε1, ε2, ε3가 서로 독립적임), 다음 공식을 도출할 수 있다.[18]

:

\begin{align}

TE & = E(Y\mid X=1)- E(Y\mid X=0)\\

CDE(m) & = E(Y\mid X=1, M=m) - E(Y\mid X=0, M=m) \\

NDE & = \sum_m [E(Y|X=1, M=m) - E(Y\mid X=0, M=m) ] P(M=m\mid X=0) \\

NIE & = \sum_m [P(M=m\mid X=1) - P(M=m\mid X=0)] E(Y\mid X=0, M=m).

\end{align}



마지막 두 방정식은 매개 공식[30][31][32]이라고 불리며, 이들은 직접 및 간접 효과에 대한 분포에 무관한 표현식을 제공하며, 오차 분포와 함수 ''f'', ''g'', ''h''가 임의적임에도 불구하고, 매개 효과는 회귀를 사용하여 데이터로부터 추정될 수 있음을 보여준다.

간접 효과의 공식

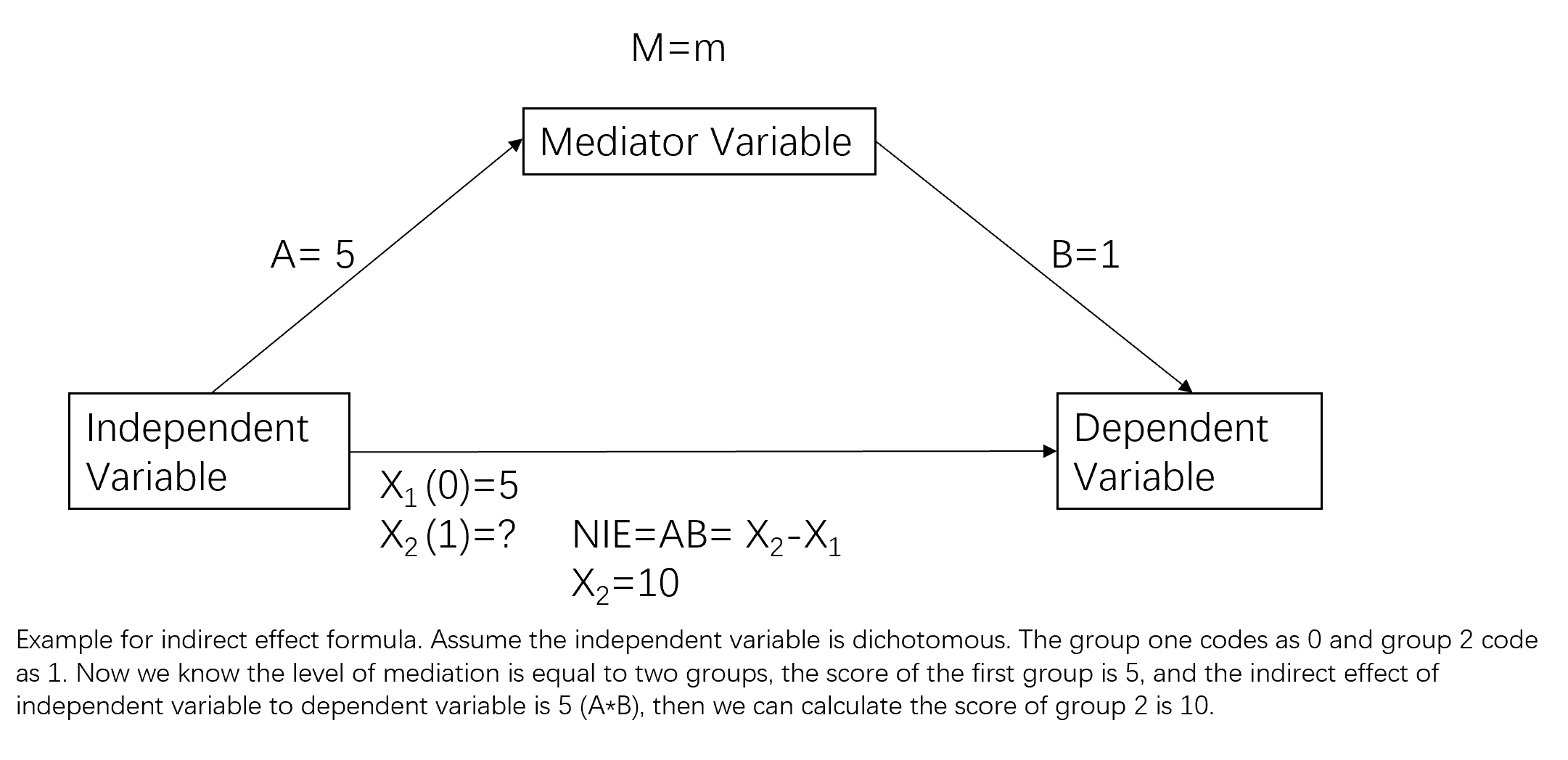
조절된 매개 및 매개 조절자의 분석은 인과 매개 분석의 특수한 경우이며, 매개 공식은 다양한 상호 작용 계수가 매개의 필요하고 충분한 구성 요소에 어떻게 기여하는지 식별한다.[29][30]

두 개의 중재 변수가 있는 직렬 중재 모델


두 개의 매개 변수 변수가 있는 병렬 매개 모델을 묘사한 개념 다이어그램.


모델이 다음과 같은 형식을 취한다고 가정한다.

:

\begin{align}

X & = \varepsilon_1 \\

M & = b_0 + b_1X + \varepsilon_2 \\

Y & = c_0 + c_1X + c_2M + c_3XM + \varepsilon_3

\end{align}



여기서 매개변수 c_3은 ''M''이 ''X''의 ''Y''에 대한 영향을 수정하는 정도를 정량화한다. 모든 매개변수가 데이터에서 추정된 경우에도, 어떤 매개변수 조합이 ''X''의 ''Y''에 대한 직접 효과와 간접 효과를 측정하는지, 또는 더 실용적으로, 총 효과 TE의 어떤 부분이 매개에 의해 설명되고 어떤 부분이 매개에 기인하는지 평가하는 방법은 여전히 명확하지 않다. 선형 분석에서 전자는 곱 b_1 c_2 / TE로 캡처되고 후자는 차이 (TE - c_1)/TE로 캡처되며 두 수량은 일치한다. 그러나 상호 작용이 있는 경우 각 분수는 매개 공식에서 정하는 대로 별도의 분석을 요구하며, 다음과 같은 결과를 얻는다.

:

\begin{align}

NDE & = c_1 + b_0 c_3 \\

NIE & = b_1 c_2 \\

TE & = c_1 + b_0 c_3 + b_1(c_2 + c_3) \\

& = NDE + NIE + b_1 c_3.

\end{align}



따라서 매개가 충분할 출력 응답의 분수는 다음과 같다.

: \frac{NIE}{TE} = \frac{b_1 c_2}{c_1 + b_0 c_3 + b_1 (c_2 + c_3)},

매개가 필요할 분수는 다음과 같다.

: 1- \frac{NDE}{TE} = \frac{b_1 (c_2 +c_3)}{c_1 + b_0c_3 + b_1 (c_2 + c_3)}.

이러한 분수는 모델의 매개변수의 명확하지 않은 조합을 포함하며, 매개 공식의 도움을 받아 기계적으로 구성할 수 있다. 중요하게도 상호 작용으로 인해, 매개변수 c_1이 사라지더라도 직접 효과가 유지될 수 있으며, 더욱이 직접 효과와 간접 효과가 모두 사라지더라도 총 효과가 유지될 수 있다. 이는 매개변수를 개별적으로 추정하는 것은 매개의 효과에 대해 거의 알려주지 않으며, 더 일반적으로 매개와 조절은 서로 얽혀 있으며 별도로 평가할 수 없음을 보여준다.

6. 비판 및 한계

Baron과 Kenny(1986)의 단계적 접근법은 유의미한 전체 효과가 없어도 매개 효과가 존재할 수 있다는 점에서 비판받는다.[9] 데이비드 A. 케니는 2019년 자신의 웹사이트에서 이를 인정하며, 1986년의 원래 접근법에서 제시된 첫 번째 단계가 반드시 필요하지 않을 수 있다고 밝혔다. Hayes(2009)는 더 나아가 완전 매개와 부분 매개의 개념에 의문을 제기하며, 고전적인 매개 단계의 폐기를 주장했다.[9]

실험적 접근 방식에서는 매개변수 조작의 윤리성, 측정의 타당성, 제3의 변수 통제 등 여러 요소를 신중하게 고려해야 한다. 매개변수를 조작하고 측정할 수 있는지, 그 과정이 윤리적인지, 측정 과정이 결과에 영향을 미치지 않는지 등을 검토해야 한다.

상관관계 연구는 인과관계를 확립하기 어렵다는 한계가 있다. 제3의 변수가 독립 변수와 종속 변수 모두에 영향을 미쳐 허위 상관관계를 만들 수 있기 때문이다. 이러한 문제를 해결하기 위해 연구자들은 시간적 선행성(독립 변수가 시간상 종속 변수보다 먼저 발생하는 것)과 비허위성(제3의 변수를 통제해도 독립 변수와 종속 변수 간의 관계가 유지되는 것) 등의 조건을 검토하여 인과관계를 추론하기도 한다.

또한, 독립 변수와 매개 변수 간의 상호작용이 존재한다면, 이는 매개가 아닌 조절 효과를 시사하는 것일 수 있다.

7. 참고 문헌


  • Baron, R. M., & Kenny, D. A. (1986). The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. ''Journal of Personality and Social Psychology'', 51(6), 1173-1182.

참조

[1] 웹사이트 Types of Variables http://www.indiana.e[...] 2016-01-25
[2] 서적 Introduction to Statistical Mediation Analysis Erlbaum
[3] 논문 Mediation analysis: a practitioner's guide 2016
[4] 서적 Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences Erlbaum
[5] 논문 The Moderator-Mediator Variable Distinction in Social Psychological Research : Conceptual, Strategic, and Statistical Considerations
[6] 서적 Statistical Methods for Psychology Cengage Learning
[7] 논문 Mediation in experimental and nonexperimental studies: New procedures and recommendations
[8] 논문 Asymptotic confidence intervals for indirect effects in structural equation models
[9] 논문 Beyond Baron and Kenny: Statistical mediation analysis in the new millennium
[10] 논문 A comparison of methods to test mediation and other intervening variable effects
[11] 웹사이트 Interactive Mediation Tests http://quantpsy.org/[...] 2022-05-05
[12] 웹사이트 Testing of Mediation Models in SPSS and SAS http://www.comm.ohio[...] Comm.ohio-state.edu 2012-05-16
[13] 웹사이트 SPSS and SAS Macro for Bootstrapping Specific Indirect Effects in Multiple Mediation Models http://www.comm.ohio[...] Comm.ohio-state.edu 2012-05-16
[14] 웹사이트 Mediation http://davidakenny.n[...] 2012-04-25
[15] 논문 Identifiability and exchangeability for direct and indirect effects
[16] 논문 A further critique of the analytic strategy of adjusting for covariates to identify biologic mediation
[17] 논문 Yes, but what's the mechanism? (don't expect an easy answer) http://www2.psych.ub[...]
[18] 간행물 Direct and indirect effects http://ftp.cs.ucla.e[...] Morgan Kaufmann
[19] 논문 Establishing a causal chain: Why experiments are often more effective than mediational analyses in examining psychological processes http://www2.psych.ub[...]
[20] 논문 When moderation is mediated and mediation is moderated
[21] 간행물 Assessing moderated mediation hypotheses: Strategies, methods, and prescriptions
[22] 논문 Do not prime hawks with doves: The interplay of construct activation and consistency of social value orientation on cooperative behavior
[23] 논문 Identifiability and exchangeability for direct and indirect effects 1992
[24] 논문 A probabilistic calculus of actions Morgan Kaufmann 1994
[25] 논문 Interpretation and identification of causal mediation http://ftp.cs.ucla.e[...]
[26] 논문 Estimating causal effects of treatments in randomized and nonrandomized studies 1974
[27] 논문 Counterfactuals and Policy Analysis in Structural Models Morgan Kaufmann 1995
[28] 논문 Identification, inference, and sensitivity analysis for causal mediation effects 2010
[29] 논문 Marginal structural models for the estimation of direct and indirect effects 2009
[30] 논문 Causal inference in statistics: An overview http://ftp.cs.ucla.e[...] 2009
[31] 논문 Imputation strategies for the estimation of natural direct and indirect effects 2012
[32] 논문 Distribution-Free Mediation Analysis for Nonlinear Models with Confounding 2012
[33] 저널 체육 분야의 인과관계 연구에서 매개변인의 효과 검증
[34] 문서 Ibid. p.34
[35] 저널 사회복지연구에서의 매개효과 검증: 예방프로그램의 효과성검증을 중심으로
[36] 서적 이기봉, 김영숙, op. cit. p.35
[37] 서적 이상균, op. cit. p.24
[38] 서적 Ibid. p.39
[39] 서적 이상균, op. cit. p.28
[40] 서적 이기봉, 김영숙, op. cit. p.37
[41] 서적 Ibid. p.41


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com