몰바이데 공식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 몰바이데 공식
3. 증명
4. 다른 삼각 항등식과의 관계
5. 삼각형의 결정 조건
6. 구면 삼각법에서의 활용
7. 원내 사변형으로의 일반화
참조

1. 개요

몰바이데 공식은 평면 삼각형의 변과 각 사이의 관계를 나타내는 삼각 함수 공식이다. 이 공식은 사인 법칙과 삼각 함수의 합과 곱을 변환하는 공식을 이용하여 증명할 수 있으며, 다른 삼각 항등식과의 관계를 통해 다양한 형태로 표현될 수 있다. 몰바이데 공식은 삼각형의 결정 조건을 검증하는 데 활용되며, 구면 삼각법과 원내 사변형으로 일반화하여 적용할 수 있다.

더 읽어볼만한 페이지

삼각형에 대한 정리 - 스튜어트 정리
스튜어트 정리는 삼각형의 변과 체바 선분 사이의 관계를 나타내는 기하학 정리이며, 아폴로니우스 정리를 포함하고 코사인 법칙을 이용하여 증명한다.
삼각형에 대한 정리 - 코사인 법칙
코사인 법칙은 삼각형의 세 변 길이와 한 각의 코사인 값 사이의 관계를 나타내는 정리로, 두 변과 사잇각으로부터 제3의 변을 구하거나 세 변의 길이로 세 각을 구할 수 있으며, 직각삼각형의 경우 피타고라스 정리로 귀결된다.
삼각법 - 사인파
사인파는 고조파가 없는 단일 주파수 파형으로, 삼각함수로 표현되며 진폭, 각진동수, 위상 등의 매개변수로 특징지어지고, 푸리에 분석을 통해 복잡한 파형으로 분해 및 합성이 가능하며, 전자공학, 음악, 물리학 등 다양한 분야에서 활용된다.
삼각법 - 편평률
편평률은 회전타원체의 납작한 정도를 나타내는 척도로, 장반축과 단반축을 이용하여 계산되며, `f = (a - b) / a`, `f' = (a - b) / b`, `n = (a - b) / (a + b)` 세 가지 형태로 정의되고, 지구를 포함한 다른 천체들의 자전 속도와 구성 물질에 따라 다르게 나타난다.

몰바이데 공식
공식 정보
몰바이데 공식에 사용되는 삼각형
유형
분야	삼각법
설명	삼각형의 변과 각도 사이의 관계
공식
공식 1	(a + b) / c = sin((α + β) / 2) / cos(γ / 2)
공식 2	(a - b) / c = sin((α - β) / 2) / sin(γ / 2)
관련 인물
관련 인물	카를 몰바이데
기타
다른 이름	몰바이데의 공식, 몰바이데의 정리, 몰바이데의 방정식
독일어	Mollweidesche Formeln

2. 몰바이데 공식

3. 증명

첫 번째 식만 증명한다. 사인 법칙과 삼각함수의 합을 곱으로 바꾸는 공식, 배각 공식을 이용하면 다음과 같다.

: $\frac{A+B}{C}=\frac{\sin a + \sin b}{\sin c}=\frac{\sin\frac{a+b}{2}\cos\frac{a-b}{2}}{\sin \frac{c}{2}\cos\frac{c}{2}}=\frac{\sin\frac{\pi-c}{2}\cos\frac{a-b}{2}}{\sin \frac{c}{2}\cos\frac{c}{2}}=\frac{\cos\left(\frac{a - b}{2}\right)}{\sin\left(\frac{c}{2}\right)}$

으로 원하는 결론을 얻는다.

4. 다른 삼각 항등식과의 관계

평면 삼각형에서 $\tfrac12\gamma = \tfrac12\pi - \tfrac12(\alpha + \beta)$ 이므로, 몰바이데 공식은 구면 삼각형에 대한 네이피어의 유사점의 극한 형태임을 더 명확하게 나타내는 형태로 번갈아 작성할 수 있다.

: $\begin{align}\frac{a + b} c&= \frac{\cos\tfrac12(\alpha - \beta)}{\cos\tfrac12(\alpha + \beta)}, \\[10mu]\frac{a - b} c&= \frac{\sin\tfrac12(\alpha - \beta)}{\sin\tfrac12(\alpha + \beta)}.\end{align}$

위 두 식을 나누어 $c$ 를 제거하면 탄젠트 법칙을 얻는다.

: $\begin{align}\frac{a + b}{a - b}= \frac{\tan\tfrac12(\alpha + \beta)}{\tan\tfrac12(\alpha - \beta)}.\end{align}$

몰바이데 공식은 반각 탄젠트만으로 표현할 수도 있다.

: $\begin{align}\frac{a + b} c&= \frac{1 + \tan\tfrac12\alpha\,\tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\,\tan\tfrac12\beta}, \\[10mu]\frac{a - b} c&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{\tan\tfrac12\alpha + \tan\tfrac12\beta},\end{align}$

또는 다음과 같이 쓸 수 있다.

: $\begin{align}\tan\tfrac12\alpha\,\tan\tfrac12\beta&= \frac{a + b - c}{a + b + c}, \\[10mu]\frac{\tan\tfrac12\alpha}{\tan\tfrac12\beta}&= \frac{\phantom{-}a - b + c}{-a + b + c}.\end{align}$

이 항등식의 각 변을 곱하면 세 변에 대한 하나의 반각 탄젠트를 얻을 수 있다.

: $\bigl({\tan\tfrac12\alpha}\bigr)^2= \frac{(a + b - c)(a - b + c)}{(a + b + c)(-a + b + c)}.$

이 식에 제곱근을 취하면 코탄젠트 법칙이 된다.

: $\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},$

여기서 $s = \tfrac12(a + b + c)$ 는 반둘레이다.

또한 이 항등식은 사인 법칙과 코사인 법칙과 동등함을 증명할 수 있다.

4. 1. 네이피어의 유사점

평면 삼각형에서

\tfrac12\gamma = \tfrac12\pi - \tfrac12(\alpha + \beta)

이므로, 이러한 항등식은 구면 삼각형에 대한 네이피어의 유사점의 극한 형태임을 더 명확하게 나타내는 형태로 번갈아 작성할 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{\cos\tfrac12(\alpha - \beta)}{\cos\tfrac12(\alpha + \beta)}, \\[10mu]\frac{a - b} c&= \frac{\sin\tfrac12(\alpha - \beta)}{\sin\tfrac12(\alpha + \beta)}.\end{align}

하나를 다른 것으로 나누어

c

를 제거하면 탄젠트 법칙이 된다.

:

\begin{align}\frac{a + b}{a - b}= \frac{\tan\tfrac12(\alpha + \beta)}{\tan\tfrac12(\alpha - \beta)}.\end{align}

반각 탄젠트만으로 몰바이데 공식은 다음과 같이 쓸 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{1 + \tan\tfrac12\alpha\,\tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\,\tan\tfrac12\beta}, \\[10mu]\frac{a - b} c&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{\tan\tfrac12\alpha + \tan\tfrac12\beta},\end{align}

또는 다음과 같이 쓸 수 있다.

:

\begin{align}\tan\tfrac12\alpha\,\tan\tfrac12\beta&= \frac{a + b - c}{a + b + c}, \\[10mu]\frac{\tan\tfrac12\alpha}{\tan\tfrac12\beta}&= \frac{\phantom{-}a - b + c}{-a + b + c}.\end{align}

이 항등식의 각 변을 곱하면 세 변에 대한 하나의 반각 탄젠트가 제공된다.

:

\bigl({\tan\tfrac12\alpha}\bigr)^2= \frac{(a + b - c)(a - b + c)}{(a + b + c)(-a + b + c)}.

이것은 제곱근을 취한 후 코탄젠트 법칙이 된다.

:

\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},

여기서

s = \tfrac12(a + b + c)

는 반둘레이다.

또한 이 항등식은 사인 법칙과 코사인 법칙과 동등함을 증명할 수 있다.

4. 2. 탄젠트 법칙

평면 삼각형에서

\tfrac12\gamma = \tfrac12\pi - \tfrac12(\alpha + \beta)

이므로, 몰바이데 공식은 구면 삼각형에 대한 네이피어의 유사점의 극한 형태임을 보여주는 다음 형태로 표현할 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{\cos\tfrac12(\alpha - \beta)}{\cos\tfrac12(\alpha + \beta)}, \\[10mu]\frac{a - b} c&= \frac{\sin\tfrac12(\alpha - \beta)}{\sin\tfrac12(\alpha + \beta)}.\end{align}

위 두 식을 나누어

c

를 제거하면 탄젠트 법칙을 얻는다.

:

\begin{align}\frac{a + b}{a - b}= \frac{\tan\tfrac12(\alpha + \beta)}{\tan\tfrac12(\alpha - \beta)}.\end{align}

몰바이데 공식은 반각 탄젠트만으로 표현할 수도 있다.

:

\begin{align}\frac{a + b} c&= \frac{1 + \tan\tfrac12\alpha\,\tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\,\tan\tfrac12\beta}, \\[10mu]\frac{a - b} c&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{\tan\tfrac12\alpha + \tan\tfrac12\beta},\end{align}

또는 다음과 같이 쓸 수 있다.

:

\begin{align}\tan\tfrac12\alpha\,\tan\tfrac12\beta&= \frac{a + b - c}{a + b + c}, \\[10mu]\frac{\tan\tfrac12\alpha}{\tan\tfrac12\beta}&= \frac{\phantom{-}a - b + c}{-a + b + c}.\end{align}

이 항등식의 각 변을 곱하면 세 변에 대한 하나의 반각 탄젠트를 얻을 수 있다.

:

\bigl({\tan\tfrac12\alpha}\bigr)^2= \frac{(a + b - c)(a - b + c)}{(a + b + c)(-a + b + c)}.

이 식에 제곱근을 취하면 코탄젠트 법칙이 된다.

:

\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},

여기서

s = \tfrac12(a + b + c)

는 반둘레이다.

몰바이데 공식은 사인 법칙 및 코사인 법칙과 동등함을 증명할 수 있다.

4. 3. 반각 공식

몰바이데 공식은 반각 탄젠트를 이용하여 다음과 같이 쓸 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{1 + \tan\tfrac12\alpha\,\tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\,\tan\tfrac12\beta}, \\[10mu]\frac{a - b} c&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{\tan\tfrac12\alpha + \tan\tfrac12\beta},\end{align}

또는 다음과 같이 표현할 수 있다.

:

\begin{align}\tan\tfrac12\alpha\,\tan\tfrac12\beta&= \frac{a + b - c}{a + b + c}, \\[10mu]\frac{\tan\tfrac12\alpha}{\tan\tfrac12\beta}&= \frac{\phantom{-}a - b + c}{-a + b + c}.\end{align}

이 항등식의 각 변을 곱하면 세 변에 대한 하나의 반각 탄젠트가 제공된다.

:

\bigl({\tan\tfrac12\alpha}\bigr)^2= \frac{(a + b - c)(a - b + c)}{(a + b + c)(-a + b + c)}.

이것은 제곱근을 취한 후 코탄젠트 법칙이 된다.

:

\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},

여기서

s = \tfrac12(a + b + c)

는 반둘레이다.

또한 이 항등식은 사인 법칙과 코사인 법칙과 동등함을 증명할 수 있다.

4. 4. 코탄젠트 법칙

평면 삼각형에서

\tfrac12\gamma = \tfrac12\pi - \tfrac12(\alpha + \beta)

이므로, 몰바이데 공식은 구면 삼각형에 대한 네이피어의 유사점의 극한 형태임을 더 명확하게 나타내는 형태로 표현할 수 있다. 몰바이데 공식에서 하나를 다른 것으로 나누어

c

를 제거하면 탄젠트 법칙을 얻을 수 있다.

:

\begin{align}\frac{a + b}{a - b}= \frac{\tan\tfrac12(\alpha + \beta)}{\tan\tfrac12(\alpha - \beta)}.\end{align}

몰바이데 공식을 반각 탄젠트만으로 표현할 수 있으며, 이를 통해 세 변에 대한 하나의 반각 탄젠트를 제공하는 항등식을 얻을 수 있다. 이 식에서 제곱근을 취하면 코탄젠트 법칙이 된다.

:

\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},

여기서

s = \tfrac12(a + b + c)

는 반둘레이다.

이 항등식은 사인 법칙과 코사인 법칙과 동등함을 증명할 수 있다.

4. 5. 사인 법칙 및 코사인 법칙

사인 법칙과 삼각함수의 합을 곱으로 바꾸는 공식, 배각 공식을 이용하면 첫 번째 식을 증명할 수 있다.

:

\frac{A+B}{C}=\frac{\sin a + \sin b}{\sin c}=\frac{\sin\frac{a+b}{2}\cos\frac{a-b}{2}}{\sin \frac{c}{2}\cos\frac{c}{2}}=\frac{\sin\frac{\pi-c}{2}\cos\frac{a-b}{2}}{\sin \frac{c}{2}\cos\frac{c}{2}}=\frac{\cos\left(\frac{a - b}{2}\right)}{\sin\left(\frac{c}{2}\right)}

평면 삼각형에서

\tfrac12\gamma = \tfrac12\pi - \tfrac12(\alpha + \beta)

이므로, 이러한 항등식은 구면 삼각형에 대한 네이피어의 유사점의 극한 형태임을 더 명확하게 나타내는 형태로 번갈아 작성할 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{\cos\tfrac12(\alpha - \beta)}{\cos\tfrac12(\alpha + \beta)}, \\[10mu]\frac{a - b} c&= \frac{\sin\tfrac12(\alpha - \beta)}{\sin\tfrac12(\alpha + \beta)}.\end{align}

하나를 다른 것으로 나누어

c

를 제거하면 탄젠트 법칙이 된다.

:

\begin{align}\frac{a + b}{a - b}= \frac{\tan\tfrac12(\alpha + \beta)}{\tan\tfrac12(\alpha - \beta)}.\end{align}

반각 탄젠트만으로 몰바이데 공식은 다음과 같이 쓸 수 있다.

:

\begin{align}\frac{a + b} c&= \frac{1 + \tan\tfrac12\alpha\,\tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\,\tan\tfrac12\beta}, \\[10mu]\frac{a - b} c&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{\tan\tfrac12\alpha + \tan\tfrac12\beta},\end{align}

또는 다음과 같이 쓸 수 있다.

:

\begin{align}\tan\tfrac12\alpha\,\tan\tfrac12\beta&= \frac{a + b - c}{a + b + c}, \\[10mu]\frac{\tan\tfrac12\alpha}{\tan\tfrac12\beta}&= \frac{\phantom{-}a - b + c}{-a + b + c}.\end{align}

이 항등식의 각 변을 곱하면 세 변에 대한 하나의 반각 탄젠트가 제공된다.

:

\bigl({\tan\tfrac12\alpha}\bigr)^2= \frac{(a + b - c)(a - b + c)}{(a + b + c)(-a + b + c)}.

이것은 제곱근을 취한 후 코탄젠트 법칙이 된다.

:

\frac{\cot\tfrac12\alpha}{s - a}= \frac{\cot\tfrac12\beta}{s - b}= \frac{\cot\tfrac12\gamma}{s - c}= \sqrt{\frac{s\vphantom{)}}{(s - c)(s - b)(s - a)}},

여기서

s = \tfrac12(a + b + c)

는 반둘레이다.

또한 이 항등식은 사인 법칙과 코사인 법칙과 동등함을 증명할 수 있다.

5. 삼각형의 결정 조건

몰바이데 공식은 삼각형의 결정 조건을 검증할 때 자주 이용된다. 먼저 A + B > C를 몰바이데 공식에 의해 풀어 쓰면,

: $\cos{\frac{a - b}{2}} > \sin{\frac{c}{2}} = \cos{\frac{a + b}{2}}$

이고, 양 변을 전개하면,

: $2\sin{\frac{a}{2}}\sin{\frac{b}{2}} > 0$

이 되는데, 이는 삼각형에서 사인의 성질에 의해 항상 성립하는 식이다. 또 A - B < C를 몰바이데 공식에 의해 풀어 쓰면,

: $\sin{\frac{a - b}{2}} < \cos{\frac{c}{2}} = \sin{\frac{a + b}{2}}$

인데 양 변을 전개하면,

: $2\cos{\frac{a}{2}}\sin{\frac{b}{2}} > 0$

이고, 이는 삼각형에서 사인과 코사인의 성질에 의해 항상 성립하는 식이다.

6. 구면 삼각법에서의 활용

구면 삼각법에서, 코사인 법칙과 네이피어의 유사점과 같은 파생된 항등식은 변을 측정하는 중심각과 꼭짓점의 이면각을 교환하는 정확한 쌍대성을 갖는다. 무한소 극한에서 변에 대한 코사인 법칙은 평면 코사인 법칙으로 축소되고 네이피어의 유사점 중 두 개는 몰바이데 공식으로 축소된다. 그러나 각도에 대한 코사인 법칙은 0 = 0 으로 퇴화한다. 변 길이의 제곱을 구면 초과 ''E''로 나누면, 0이 아닌 비율, 즉 구면 삼각법 관계를 얻는다.

: $\begin{align}\frac{\tan^2\tfrac12c}{\tan\tfrac12E}= \frac{\sin\gamma}{\sin\alpha\,\sin\beta}.\end{align}$

무한소 극한에서, 구면 변의 반각 탄젠트가 평면 변의 길이로 축소됨에 따라, 구면 초과의 반각 탄젠트는 평면 삼각형의 넓이 ''A''의 두 배로 축소되므로, 평면에서는 다음과 같다.

: $\frac{c^2}{2A} = \frac{\sin\gamma}{\sin\alpha\,\sin\beta},$

마찬가지로 ''a''와 ''b''에 대해서도 적용된다.

결과로서 (위의 공식을 ''a''와 ''b''에 대해 곱하거나 나눔으로써) 몰바이데 공식에 대한 두 개의 쌍대 명제를 얻는다. 첫 번째는 두 변과 끼인 각도로 넓이를 표현하고, 다른 하나는 사인 법칙이다.

: $\frac{ab}{2A} = \frac{1}{\sin\gamma},$

: $\frac{a}{b} = \frac {\sin\alpha}{\sin\beta}.$

두 번째 공식을 몰바이데 공식 중 하나에 더 가까운 형태로 번갈아 표현할 수 있다 (다시 탄젠트 법칙).

: $\frac{\tan\tfrac12(\alpha + \beta)}{\cot\tfrac12\gamma} = \frac{a - b}{a + b}.$

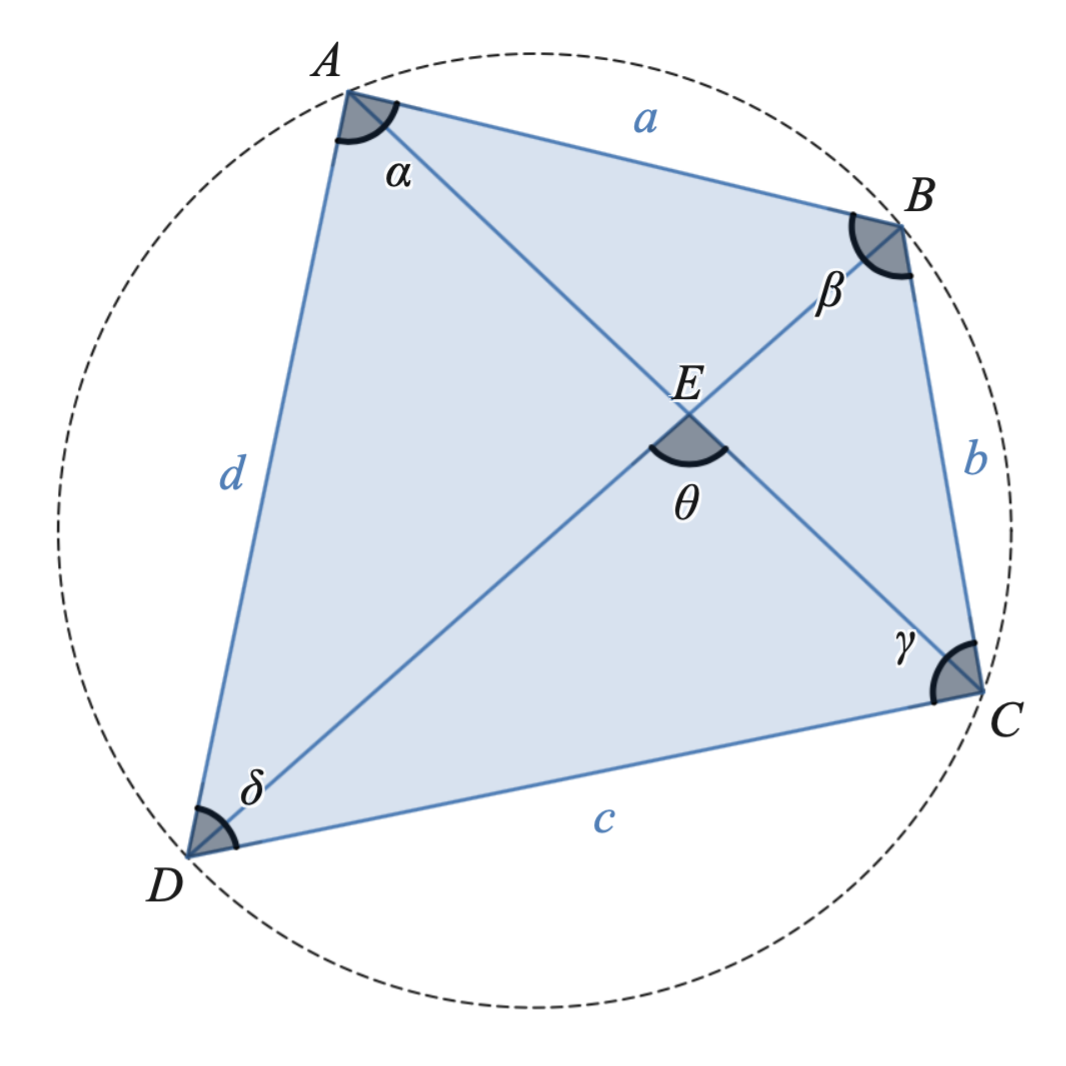
7. 원내 사변형으로의 일반화

몰바이데 공식의 일반화는 원내 사변형

\square ABCD

에 대해 성립한다.^[5] 변의 길이를

|AB| = a,

|BC| = b,

|CD| = c,

및

|DA| = d

로 나타내고, 각의 크기를

\angle{DAB} = \alpha,

\angle{ABC} = \beta,

\angle{BCD} = \gamma,

및

\angle{CDA} = \delta

로 나타낸다. 만약

E

가 대각선의 교점이라면,

\angle{CED} = \theta

로 나타낸다. 그러면:

:

\begin{align}\frac{a+c}{b+d}&= \frac{\sin\tfrac12(\alpha+\beta)}{\cos\tfrac12(\gamma-\delta)}\tan\tfrac12\theta, \\[10mu]\frac{a-c}{b-d}&= \frac{\cos\tfrac12(\alpha+\beta)}{\sin\tfrac12(\delta-\gamma)}\cot\tfrac12\theta.\end{align}

원내 사변형의 항등식을 기반으로 대체하여 여러 변형 공식을 구성할 수 있다.

:

\begin{align}\sin\tfrac12(\alpha+\beta) = \phantom-\cos\tfrac12(\beta-\gamma)= \phantom-\sin\tfrac12(\gamma+\delta) = \cos\tfrac12(\delta-\alpha), \\[3mu]\cos\tfrac12(\alpha+\beta) = -\sin\tfrac12(\beta-\gamma)= -\cos\tfrac12(\gamma+\delta) = \sin\tfrac12(\delta-\alpha).\end{align}

두 인접한 각도의 반각 탄젠트 측면에서 유리식 관계로서, 이 공식들은 다음과 같이 작성할 수 있다.

:

\begin{align}\frac{a+c}{b+d}&= \frac{\tan\tfrac12\alpha +  \tan\tfrac12\beta}{1 + \tan\tfrac12\alpha\, \tan\tfrac12\beta}\tan\tfrac12\theta, \\[10mu]\frac{b-d}{a-c}&= \frac{\tan\tfrac12\alpha - \tan\tfrac12\beta}{1 - \tan\tfrac12\alpha\, \tan\tfrac12\beta}\tan\tfrac12\theta.\end{align}

삼각형은 길이가 0인 한 변을 가진 사변형으로 간주할 수 있다. 이러한 관점에서

d

가 0에 가까워짐에 따라, 원내 사변형은 삼각형

\triangle A'B'C'

로 수렴하고, 위의 공식은 유사한 삼각형 공식으로 단순화된다. 삼각형에 대한 규칙에 맞게 다시 레이블을 지정하면, 극한에서

a' = b,

b' = c,

c' = a,

\alpha' = \alpha + \delta - \pi = \pi - \theta,

\beta' = \beta,

및

\gamma' = \gamma

가 된다.

참조

_[1] 서적 Plane Trigonometry and Applications Allyn and Bacon
_[2] 서적 Trigonometry Dellen
_[3] 간행물 Discussions: Geometric Proofs of the Law of Tangents
_[4] 서적 Plane Trigonometry and Applications Allyn and Bacon
_[5] 간행물 A generalization of Mollweide's formula (rather Newton's) http://matinf.upit.r[...] 2023-12-29

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com