분할 상환 분석
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
분할 상환 분석은 알고리즘의 전체적인 성능을 평가하는 방법으로, 개별 연산의 최악의 경우를 분석하는 대신 연산 빈도와 비용, 연산 간의 관계를 고려한다. 1985년 로버트 타잔의 논문에서 처음 공식화되었으며, 총계 분석, 회계 방식, 잠재적 방법 등의 분석 방법이 있다. 이진 카운터 증가, 동적 배열, 큐 등 다양한 자료구조 및 알고리즘의 분석에 활용되며, 온라인 알고리즘 설계에도 유용하다.
더 읽어볼만한 페이지
- 분할 상환 자료 구조 - 스플레이 트리
스플레이 트리는 스플레이 연산을 통해 자가 균형을 유지하며 최근 접근 노드의 빠른 접근을 가능하게 하는 이진 탐색 트리로, 분할 상환 분석 시 평균적으로 O(log n)의 시간 복잡도를 가진다. - 분할 상환 자료 구조 - 피보나치 힙
피보나치 힙은 최소 힙 속성을 가진 트리들의 집합으로, 각 노드의 차수를 특정 로그 값 이하로 유지하여 효율적인 삽입, 병합, 최소값 검색 연산을 지원하며, 다익스트라 알고리즘과 같은 그래프 알고리즘의 성능 향상에 활용된다. - 알고리즘 분석 - 계산 복잡도
계산 복잡도는 알고리즘의 효율성을 평가하는 척도로, 시간, 공간 등의 자원을 고려하며, 입력 크기의 함수로 표현되고, 빅 오 표기법을 사용하여 알고리즘의 예상 성능을 파악하는 데 중요한 역할을 한다. - 알고리즘 분석 - 비결정적 알고리즘
비결정적 알고리즘은 계산 과정에서 여러 선택지를 가질 수 있는 비결정론적 튜링 기계 또는 비결정성을 활용하는 프로그래밍 패러다임인 비결정론적 프로그래밍과 관련된 알고리즘을 포괄적으로 지칭한다.
| 분할 상환 분석 | |
|---|---|
| 개요 | |
| 분야 | 전산학 |
| 하위 분야 | 알고리즘 분석 |
| 관련 주제 | 계산 복잡도 이론 알고리즘 효율성 최악의 경우 성능 평균적인 성능 점근 표기법 상각 비용 |
| 상각 분석 | |
| 목표 | 알고리즘의 성능 평가 |
| 특징 | 일련의 연산에 대한 평균 비용을 분석 |
| 장점 | 최악의 경우 분석보다 더 정확한 성능 예측 가능 |
| 단점 | 개별 연산의 실제 비용을 숨길 수 있음 |
| 적용 분야 | 자료 구조, 알고리즘 설계, 성능 최적화 |
| 방법 | |
| 집계 방법 | 모든 연산의 총 비용을 계산하고 연산 횟수로 나눔 |
| 회계 방법 | 각 연산에 상각 비용을 할당하고, 나중에 사용할 수 있도록 일부 비용을 저축 |
| 잠재적 방법 | 자료 구조의 상태를 나타내는 잠재적 함수를 사용하여 상각 비용을 계산 |
2. 역사
분할 상환 분석은 총계 분석(aggregate analysis)이라는 기법에서 유래되었으며, 현재는 총계 분석을 포함하는 더 넓은 개념으로 사용된다. 이 기법은 1985년 로버트 타잔의 논문 "분할 상환 계산 복잡도(Amortized Computational Complexity)"에서 처음으로 공식화되었다.[3][2] 이 논문에서는 기존에 흔히 사용되던 확률론적 방식보다 유용한 형태의 분석 방법론이 필요하다는 점을 시사하고 있다. 초기에는 분할 상환(Amortization) 방식은 이진 트리, 합집합-찾기 연산 등 특정 자료구조 및 알고리즘에 주로 사용되었으나, 현재는 다양한 알고리즘 분석에 널리 활용된다.[2]
분할 상환 분석은 특정 연산의 빈도와 비용, 그리고 연산 간의 관계를 고려하여 전체적인 성능을 평가하는 방법이다. 주로 연산들 사이에서 계속 유지되는 상태를 가지는 자료 구조를 분석하는 데 사용된다. 최악의 경우(Worst case) 연산이 발생하면, 해당 연산이 긴 시간 동안 다시는 일어나지 않도록 상태를 변경하여 비용을 "분할 상환"하는 아이디어를 기반으로 한다.
3. 방법
분할 상환 분석을 수행하는 대표적인 방법은 다음과 같다.
위의 방법들은 모두 동일한 결과를 제공하며, 상황에 따라 더 편리한 방법을 선택하여 사용한다.[4]
3. 1. 총계 분석 (Aggregate Analysis)
n개의 연산 시퀀스에 대한 총 비용 T(n)의 상한을 구한 후, 분할 상환 비용을 T(n) / n으로 계산한다. 모든 연산에 대해 동일한 분할 상환 비용을 적용한다.
예시: 이진 카운터 증가 (Incrementing a Binary Counter)
초기값 0에서 시작하는 이진 카운터에서 n번의 INCREMENT 연산을 수행할 때, 각 비트가 반전되는 횟수는 다음과 같다.
i >= k인 비트 A[i]는 존재하지 않으므로 반전될 수 없다. 따라서 n번의 연산에서 뒤집히는 총 횟수는 최대 2n이다.[1] 그러므로 초기값 0을 가지는 카운터에 대한 n개의 INCREMENT 연산 시퀀스의 최악의 경우 수행 시간은 O(n)이다. 각 연산에 대한 평균 비용, 즉 분할 상환 비용은 O(n)/n = O(1)이다.
3. 2. 회계 방식 (Accounting Method)
회계 방법은 각 연산에 실제 비용과 다를 수 있는 분할 상환 비용을 할당하는 분석 방법이다. 초기 연산에서 실제 비용보다 높은 분할 상환 비용을 할당하여 "크레딧"을 축적하고, 이를 나중에 실제 비용이 높은 연산에 사용한다.
예를 들어, 0부터 시작하는 이진 카운터의 INCREMENT 연산을 생각해보자. 이 연산의 수행 시간은 비트를 반전시키는 횟수에 비례한다. 분할 상환 분석을 위해 비트 하나를 1로 설정하는 데 2USD의 분할 상환 비용을 부과한다. 비트가 1이 될 때 1USD는 해당 비트를 1로 만드는 비용으로 지불하고, 나머지 1USD는 나중에 해당 비트를 0으로 반전시킬 때 사용하기 위해 해당 비트 위에 둔다.
이렇게 하면 카운터의 모든 1은 자신 위에 1USD의 크레딧을 가지게 되고, 비트를 다시 0으로 만들 때는 추가 비용이 필요 없다. 즉, 비트를 0으로 만들 때는 그 비트 위에 있는 1USD로 비용을 지불하면 된다.
INCREMENT 연산에서 while 루프를 통해 비트를 0으로 만드는 비용은 해당 비트 위에 놓인 1USD로 지불할 수 있다. INCREMENT 프로시저는 최대 하나의 비트만 1로 바꾸므로, INCREMENT 연산의 분할 상환 비용은 최대 2USD이다. 카운터에서 1인 비트의 개수는 항상 0보다 크거나 같으므로, 크레딧의 총합은 항상 0보다 크거나 같다.
따라서 n개의 INCREMENT 연산에 대한 분할 상환 비용의 총합은 O(n)이며, 이는 실제 비용 총합의 상한이 된다.
3. 3. 잠재 비용 방식 (Potential Method)
잠재 비용 방법은 회계 방법과 유사하지만, "크레딧" 대신 "잠재 비용"이라는 개념을 사용한다. 잠재 비용은 자료 구조의 상태에 대한 함수로 계산되며, 분할 상환 비용은 즉시 비용에 잠재 비용의 변화를 더한 값이다.[4]
잠재 비용 방법은 초기의 자료 구조 D0에서 시작하여 n개의 연산을 수행한다. i=1,2,…,n에 대해 ci는 i번째 연산의 실제 비용을, Di는 자료 구조 Di-1에 i번째 연산을 적용한 결과로 만들어진 자료 구조를 나타낸다. 잠재적 비용 함수 Ф는 각 자료 구조 Di를 실수 Ф(Di)에 대응시키는데, 그 숫자는 자료 구조 Di와 연관된 잠재 비용이다. 잠재 비용 함수 Ф에 대한 i번째 연산의 분할 상환 비용은 각 연산들의 분할 상환 비용은 실제 비용에 그 연산으로 인한 잠재 비용의 변화를 더한 값이다.
i번째 INCREMENT 연산을 수행한 후의 카운터 잠재 비용을 bi라 하고, 이 값을 i번째 연산 이후의 카운터에서 1의 개수로 정의한다. INCREMENT 연산이 ti개의 비트를 0으로 재설정했다고 가정하면, 재설정된 ti개의 비트들 외에 최대 한 개의 비트가 1로 더 설정될 수 있으므로 이 연산의 실제 비용은 최대 ti+1이 된다.
bi=0이라면 i번째 연산은 모든 k개의 비트를 재설정하므로 bi-1=ti=k가 된다. bi>0이면, bi=bi-1-ti+1이다. 어느 경우라도 bi<=bi-1-ti+1이고 잠재 비용의 차이는 1-ti가 되며, 분할 상환 비용은 2가 된다.
카운터가 0에서 시작했다면 Ф(D0)=0이 된다. 모든 i에 대해 Ф(Di)>=0이므로 연속된 n개의 INCREMENT 연산의 총 분할 상환 비용은 실제 총 비용의 상한이고 n개의 INCREMENT 연산의 최악의 경우의 비용은 O(n)이다.
4. 예시
=== 동적 배열 (Dynamic Array) ===
동적 배열은 요소가 추가됨에 따라 크기가 동적으로 증가하는 배열로, Java의 ArrayList나 C++의 std::vector가 대표적인 예시이다. 초기 크기가 4인 동적 배열에 4개의 요소를 삽입하는 연산은 상수 시간이 소요되지만, 다섯 번째 요소는 더 큰 용량을 확보하고 기존 요소를 옮겨야 하므로 많은 시간이 소요된다. 용량이 부족할 때 두 배로 용량을 늘린다고 가정하면, 저장된 요소의 개수가 2의 거듭제곱이 될 때 O(n)의 비용이 소요되고, 그 외에는 상수 시간이 소요된다.[4]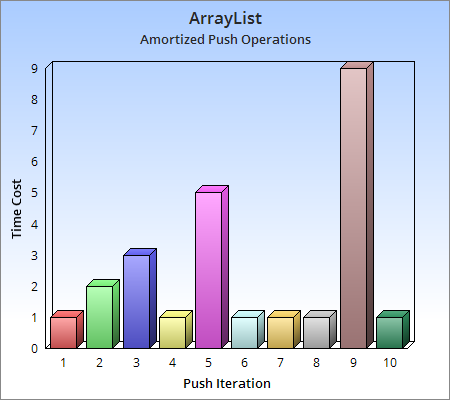
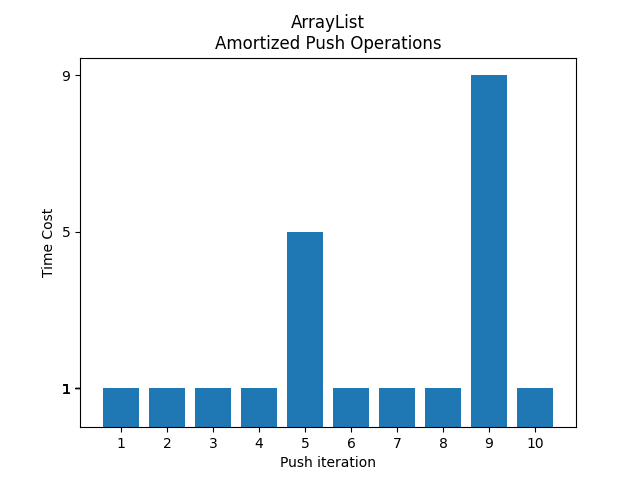
일반적으로 초기 크기가 정해진 배열에 n번의 푸시 연산을 수행하면 배열을 두 배로 늘리는 단계의 시간은 기하 급수로 O(n)이 되고, 나머지 푸시 연산의 상수 시간도 O(n)이 된다. 따라서 푸시 연산당 평균 시간은 O(n)/n = O(1)이므로, 분할 상환 분석을 통해 전체적인 삽입 연산의 평균 비용은 상수 시간(O(1))임을 알 수 있다.[8]
=== 큐 (Queue) ===
큐는 FIFO (First-In, First-Out) 방식으로 동작하는 자료 구조이다. 삽입 연산(enqueue)은 일반적으로 상수 시간에 수행되지만, 삭제 연산(dequeue)은 출력 배열이 비어 있을 경우 입력 배열의 모든 요소를 출력 배열로 이동해야 하므로 O(n) 시간이 소요될 수 있다.
enqueue 연산은 요소를 input 배열에 넣으므로 상수 시간에 실행된다. dequeue 연산은 output 배열에 요소가 있으면 상수 시간에 실행되지만, 그렇지 않으면 input 배열에서 output 배열로 모든 요소를 추가하는 데 O(n) 시간이 걸린다. (n은 input 배열의 현재 길이)
input에서 n개의 요소를 복사한 후, output 배열이 다시 비워지기 전까지 n번의 dequeue 연산을 상수 시간에 수행할 수 있다. 따라서 n개의 dequeue 연산은 O(n) 시간에 수행될 수 있으며, 이는 각 dequeue 연산의 상각 시간이 O(1)임을 의미한다.[5]
4. 1. 동적 배열 (Dynamic Array)
동적 배열은 요소가 추가됨에 따라 크기가 동적으로 증가하는 배열이다. Java의 ArrayList나 C++의 std::vector가 대표적인 예이다. 크기가 4인 동적 배열에서 시작하여 4개의 요소를 배열 끝에 삽입(pushback)하는 연산은 상수 시간이 소요된다. 그러나 다섯 번째 요소는 자리가 없어 더 큰 용량을 새롭게 확보하고 기존 요소를 옮겨야 하므로 비교적 많은 시간이 소요된다. 용량이 부족할 때 두 배로 용량을 늘린다고 가정하면, 최초 용량이 4이므로 용량이 8인 공간을 확보한 다음 기존 배열에 저장되었던 요소들을 새 배열로 옮기는 작업이 필요하다. 그 다음부터는 상수 시간이 소요된다. 즉, 상수 비용이 소요되다가 저장된 요소의 개수가 2의 거듭제곱이 되면 O(n)의 비용이 소요된다.[4]일반적으로 초기 크기가 어떤 배열에 대해 임의의 수 n만큼 푸시하면 배열을 두 배로 늘리는 단계의 시간은 기하 급수로 O(n)이 되고, 각 나머지 푸시의 상수 시간도 O(n)이 된다. 따라서 푸시 연산당 평균 시간은 O(n)/n = O(1)이다. 이러한 이유로 분할 상환 분석을 통해 전체적인 삽입 연산의 평균 비용은 상수 시간(O(1))임을 알 수 있다.[8]
4. 2. 큐 (Queue)
큐는 FIFO (First-In, First-Out) 방식으로 동작하는 자료 구조이다. 삽입 연산(enqueue)은 일반적으로 상수 시간에 수행되지만, 삭제 연산(dequeue)은 출력 배열이 비어 있을 경우 입력 배열의 모든 요소를 출력 배열로 이동해야 하므로 O(n) 시간이 소요될 수 있다.다음은 큐의 Python3 구현 예시이다.
class Queue:
# 큐를 두 개의 빈 리스트로 초기화합니다.
def __init__(self):
self.input = [] # 인큐(enqueue)된 요소를 저장합니다.
self.output = [] # 디큐(dequeue)된 요소를 저장합니다.
def enqueue(self, element):
self.input.append(element) # 요소를 input 리스트에 추가합니다.
def dequeue(self):
if not self.output: # output 리스트가 비어있는 경우
# input 리스트의 모든 요소를 output 리스트로 옮기면서 순서를 뒤집습니다.
while self.input: # input 리스트가 비어있지 않은 동안
self.output.append(self.input.pop()) # input 리스트의 마지막 요소를 꺼내 output 리스트에 추가합니다.
return self.output.pop() # output 리스트의 마지막 요소를 꺼내 반환합니다.
enqueue 연산은 단순히 요소를 input 배열에 넣으므로 상수 시간에 실행된다. 그러나 dequeue 연산은 output 배열에 이미 요소가 있는 경우에는 상수 시간에 실행되지만, 그렇지 않으면 input 배열에서 output 배열로 모든 요소를 추가하는 데 O(n) 시간이 걸린다. 여기서 n은 input 배열의 현재 길이이다.
input에서 n개의 요소를 복사한 후, output 배열이 다시 비워지기 전까지 각각 상수 시간이 걸리는 n개의 dequeue 연산을 수행할 수 있다. 따라서 n개의 dequeue 연산 시퀀스를 O(n) 시간에만 수행할 수 있으며, 이는 각 dequeue 연산의 상각 시간이 O(1)임을 의미한다.[5]
또는, input 배열에서 output 배열로 항목을 복사하는 비용을 해당 항목에 대한 이전 enqueue 연산에 부과할 수 있다. 이 부과 방식은 enqueue에 대한 상각 시간을 두 배로 늘리지만 dequeue에 대한 상각 시간을 O(1)로 줄인다.
5. 활용
분할 상환 분석은 알고리즘의 성능을 보다 정확하게 평가하고, 효율적인 자료 구조 및 알고리즘을 설계하는 데 도움을 준다. 특히, 온라인 알고리즘 설계 및 분석에 유용하게 활용된다.[1] "분할 상환 알고리즘"은 일반적으로 분할 상환 분석을 통해 성능이 우수하다고 입증된 알고리즘을 의미한다.[2]
참조
[1]
웹사이트
Lecture 18: Amortized Algorithms
https://www.cs.corne[...]
Cornell University
2006
[2]
간행물
Amortized Analysis Explained
http://www.cs.prince[...]
2011-05-03
[3]
논문
Amortized Computational Complexity
http://www.cs.duke.e[...]
1985-04
[4]
웹사이트
CS 3110 Lecture 20: Amortized Analysis
http://www.cs.cornel[...]
Cornell University
2011
[5]
웹사이트
CSE332: Data Abstractions
http://courses.cs.wa[...]
[6]
웹사이트
Lecture 7: Amortized Analysis
https://www.cs.cmu.e[...]
2015-03-14
[7]
간행물
Amortized Analysis Explained
http://www.cs.prince[...]
2011-05-03
[8]
웹사이트
Lecture 20: Amortized Analysis
http://www.cs.cornel[...]
Cornell University
[9]
웹사이트
Lecture 20: Amortized Analysis
http://www.cs.cornel[...]
Cornell University
[10]
웹사이트
CSE332: Data Abstractions
http://courses.cs.wa[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com