뷔퐁의 바늘

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 풀이
- 2.1. 짧은 바늘 (l < t)
- 2.2. 긴 바늘 (l > t)
3. 초등 미적분학을 이용한 풀이 (짧은 바늘)
4. 적분 없이 해결 (짧은 바늘)
5. 라플라스의 확장
6. 원주율(π) 추정
7. 라차리니의 실험
8. 시뮬레이션
- 8.1. 시뮬레이션 시 주의사항: 의존성 문제
참조

1. 개요

뷔퐁의 바늘은 평행선이 그어진 바닥에 바늘을 떨어뜨렸을 때, 바늘이 선과 교차할 확률을 계산하는 문제이다. 바늘의 길이와 선 사이의 간격에 따라 확률 계산 방식이 달라지며, 짧은 바늘(l < t)의 경우, 교차 확률은 2l/(tπ)로 계산된다. 이 문제를 통해 원주율(π)의 근사값을 구할 수 있으며, 몬테카를로 방법을 활용한 시뮬레이션이 가능하다. 뷔퐁의 바늘 문제는 라플라스에 의해 확장되었으며, 원주율 추정에 대한 라차리니의 실험은 확증 편향의 예시로 여겨지기도 한다. 시뮬레이션을 통해 원주율을 추정할 때는 원주율에 대한 의존성을 피하기 위한 방법이 사용된다.

더 읽어볼만한 페이지

응용확률론 - 자급자족
자급자족은 개인이 스스로 생산한 것만 소비하며 자립적 건축, 지속 가능한 농업, 재생 에너지 등을 통해 실현되는 지속 가능한 삶의 방식이다.
응용확률론 - 진폭 편이 방식
진폭 편이 방식(ASK)은 반송파의 진폭을 변화시켜 데이터를 표현하는 변조 방식이며, 온오프 변조와 다치 ASK가 있으며, 오류 확률은 다양한 요인에 의해 영향을 받는다.
확률론 - 확률 밀도 함수
확률 밀도 함수는 연속 확률 변수의 확률 분포를 나타내는 함수로, 특정 구간에서 확률 변수가 값을 가질 확률은 해당 구간에 대한 함수의 적분으로 계산되며, 통계적 특성 계산 및 변수 변환 등에 활용되어 불확실성 모델링 및 분석에 중요한 역할을 한다.
확률론 - 체비쇼프 부등식
체비쇼프 부등식은 확률 변수가 평균에서 얼마나 멀리 떨어져 있는지에 대한 확률의 상한을 제공하는 부등식으로, 이레네-쥘 비네메가 처음 공식화하고 체비쇼프와 안드레이 마르코프에 의해 일반화 및 증명되었으며, 확률론적 표현 외에도 측도 공간에 대한 명제로 확장될 수 있다.

뷔퐁의 바늘
개요
이름	뷔퐁의 바늘 문제
분야	기하 확률
관련 인물	조르주루이 르클레르 드 뷔퐁
문제
내용	길이가 l인 바늘을 평행선이 a 간격으로 그어진 평면에 무작위로 떨어뜨릴 때, 바늘이 선과 교차할 확률을 구하는 문제
조건	a > l
확률	p = (2l)/(aπ)
일반화
면	바늘이 구부러지거나 연결된 선분으로 이루어진 경우에도 적용 가능
공식	p = (2L)/(aπ), 여기서 L은 바늘의 길이
몬테카를로 방법
π 값 추정	뷔퐁의 바늘 문제를 통해 π 값을 추정 가능
공식	π ≈ (2L)/(ap)
역사
최초 제시	1777년 조르주루이 르클레르 드 뷔퐁이 제시
수학적 엄밀성	19세기 후반에 수학적 엄밀성을 갖춤
관련 연구	조지프 버트런드, 모건 크로프턴, 줄리오 체사레 바르비에리, 제임스 조지프 실베스터 등의 연구

2. 풀이

뷔퐁의 바늘 문제는 바늘을 떨어뜨려 특정 조건을 만족하는 확률을 구하는 문제이다. 이 문제는 기하학적 확률의 예시로, 적분을 사용하여 풀 수 있다.

문제를 수학적으로 표현하면 다음과 같다. 길이 *l*의 바늘을 간격 *t*인 평행선들 위에 떨어뜨릴 때, 바늘이 선과 교차할 확률은 얼마인가?

바늘의 중심에서 가장 가까운 평행선까지의 거리를 *x*, 바늘과 평행선이 이루는 각도를 θ라고 정의한다.

x*는 0과 *t*/2 사이의 값을 가지며, 균등 확률 분포 함수는 다음과 같다.

조건	확률 밀도 함수
0 ≤ x ≤ t/2	2/t
그 외	0

θ는 0과 π/2 사이의 값을 가지며, 균등 확률 분포 함수는 다음과 같다.

조건	확률 밀도 함수
0 ≤ θ ≤ π/2	2/π
그 외	0

두 확률 변수 *x*와 θ는 서로 독립이므로, 결합 확률 밀도 함수는 다음과 같다.

조건	결합 확률 밀도 함수
0 ≤ x ≤ t/2, 0 ≤ θ ≤ π/2	4/(tπ)
그 외	0

바늘이 선을 가로지르는 조건은 다음과 같다.^[4]

: $x \le \frac{l}{2}\sin\theta.$

이후의 풀이는 바늘의 길이에 따라 '짧은 바늘'(l < t)과 '긴 바늘'(l > t)의 두 가지 경우로 나뉜다.

2. 1. 짧은 바늘 (l < t)

l^영어 < t^영어일 때, 결합확률분포함수를 적분하면 다음과 같다.

:

P = \int_{\theta=0}^{\frac{\pi}{2}} \int_{x=0}^{(l/2)\sin\theta}  \frac{4}{t\pi}\,dx\,d\theta = \frac{2 l}{t\pi}.

이 결과는 "뷔퐁의 국수"를 이용해서 도출할 수도 있다. 좀 더 수학적인 용어로 문제를 표현하면 다음과 같다. 길이가 l^영어인 바늘을 평행선 간격이 t^영어인 평면에 떨어뜨렸을 때, 바늘이 착지 시 선을 가로지를 확률은 얼마인가?

x^영어를 바늘의 중심에서 가장 가까운 평행선까지의 거리, θ^영어를 바늘과 평행선 중 하나가 이루는 예각이라고 하자.

0과 사이의 x^영어에 대한 균등 확률 밀도 함수(PDF)는 다음과 같다.

:

f_X(x)=\begin{cases}\dfrac{2}{t} &:\ 0 \le x \le \dfrac{t}{2}\\[4px]0 &: \text{elsewhere.}\end{cases}

여기서 은 선 위에 직접 중심이 놓인 바늘을, 는 두 선 사이에 완벽하게 중심이 놓인 바늘을 나타낸다. 균등 PDF는 바늘이 이 범위 내 어디든 떨어질 확률은 동일하지만, 그 범위를 벗어날 수는 없다고 가정한다.

0과 사이의 θ^영어에 대한 균등 확률 밀도 함수는 다음과 같다.

:

f_\Theta(\theta)=\begin{cases}\dfrac{2}{\pi} &:\ 0 \le \theta \le \dfrac{\pi}{2}\\[4px]0 &: \text{elsewhere.}\end{cases}

여기서 은 표시된 선과 평행한 바늘을, 라디안은 표시된 선에 수직인 바늘을 나타낸다. 이 범위 내의 모든 각도는 동일하게 나타날 가능성이 있는 결과로 간주된다.

두 확률 변수 x^영어와 θ^영어는 서로 독립적이므로,^[4] 결합 확률 분포는 다음과 같다.

:

f_{X,\Theta}(x,\theta)=\begin{cases}\dfrac{4}{t\pi} &:\ 0 \le x \le \dfrac{t}{2}, \ 0 \le \theta \le \dfrac{\pi}{2}\\[4px]0 &: \text{elsewhere.}\end{cases}

바늘이 선을 가로지르는 경우는 다음과 같다.

:

x \le \frac {l}{2} \sin\theta.

선이 바늘과 교차할 확률은 결합 확률 밀도 함수를 적분하여 구할 수 있다.

:

P = \int_{\theta=0}^\frac{\pi}{2} \int_{x=0}^{\frac{l}{2}\sin \theta}  \frac{4}{t\pi}\,dx\,d\theta = \frac{2 l}{t\pi}.

이 식을 사용하여 몬테카를로 방법으로 원주율의 근사값을 구할 수 있다. 바늘을

n

회 떨어뜨렸을 때 바늘과 선이

h

회 교차했다고 하면,

:

\frac{h}{n} \sim \frac{2 l}{t\pi},

이므로

\pi

의 값은

:

\pi \sim \frac{2{l}n}{th}.

로 근사할 수 있다.

2. 2. 긴 바늘 (l > t)

l > t

일 때, 결합확률분포함수를 적분하면 다음과 같다.

:

\int_{\theta=0}^{\frac{\pi}{2}} \int_{x=0}^{m(\theta)}  \frac{4}{t\pi}\,dx\,d\theta ,

이때

m(\theta)

는 범위

\theta = \left[ {l \over 2} \sin \theta , {t \over 2} \right]

의 최솟값이다.

위 적분을 수행하면

t < l

일 때, 바늘이 선을 가로지를 확률은

:

\frac{2 l}{t\pi} - \frac{2}{t\pi}\left\{\sqrt{l^2 - t^2} + t\sin^{-1}\left(\frac{t}{l}\right)\right\}+1

또는

:

\frac{2}{\pi} \cos^{-1}\frac{t}{l} + \frac{2}{\pi} \frac{l}{t} \left\{1 - \sqrt{1 - \left( \frac{t}{l} \right)^2  } \right\}.

두 번째 표현에서, 제1항은 바늘이 적어도 한 개의 선과 겹치게 되는 각도가 나올 확률을 나타낸다. 제2항은 바늘이 위치에 따라 선과 겹칠 수도 있고 안 겹칠 수도 있을 때 그 위치가 겹치는 위치가 될 확률을 나타낸다.

3. 초등 미적분학을 이용한 풀이 (짧은 바늘)

$l < t$ 일 때, 결합확률분포함수를 적분하면 다음과 같다.

: $P = \int_{\theta=0}^{\frac{\pi}{2}} \int_{x=0}^{(l/2)\sin\theta} \frac{4}{t\pi}\,dx\,d\theta = \frac{2 l}{t\pi}.$

이 결과는 뷔퐁의 국수를 이용해서 도출할 수도 있다.

다음은 "짧은 바늘" 경우에 대한 해법으로, 위의 해법과 동일하지만 시각적인 면이 더 강하고 반복 적분을 피한다.

확률 P는 두 확률의 곱으로 계산할 수 있다. P = P₁ · P₂인데, 여기서 P₁은 바늘의 중심이 바늘이 교차할 수 있을 정도로 선에 가깝게 떨어질 확률이고, P₂는 중심이 닿을 수 있는 거리에 있을 때 바늘이 실제로 선을 교차할 확률이다.

위 섹션의 그림을 보면, 바늘의 중심이 스트립의 양쪽에서 $\frac{l}{2}$ 단위 이내에 있으면 바늘이 선을 교차할 수 있다는 것이 분명하다. 양쪽에서 $\frac{l}{2} + \frac{l}{2}$ 를 더하고 전체 너비 t로 나누면 P₁ = $\frac{l}{t}$ 가 된다.

빨간색과 파란색 바늘은 모두 x에 중심이 있다. 빨간색 바늘은 양쪽에 2θ의 각도로 포함된 회색 영역 안에 떨어져 수직선을 교차한다. 파란색 바늘은 그렇지 않다. 원의 회색 부분의 비율은 중심 x가 0에서 1까지 갈 때 적분되는 것이다.

이제 중심이 스트립의 가장자리에 닿을 수 있다고 가정하고 P₂를 계산한다. 계산을 단순화하기 위해

l = 2

라고 가정할 수 있다.

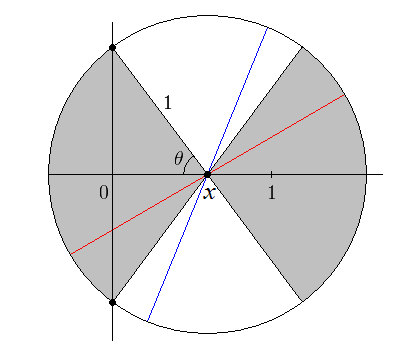
이 섹션의 그림과 같이 x와 θ를 사용한다. 바늘의 중심을 x에 놓으면, 바늘은 가능한 방향 π 라디안 중 2θ 라디안 범위 내에 떨어지면 수직 축을 교차한다. 이것은 그림에서 x의 왼쪽에 있는 회색 영역을 나타낸다. 고정된 x의 경우, θ를 x의 함수로 표현할 수 있다: θ(x) = arccos(x). 이제 x를 0에서 1까지 범위로 지정하고 적분할 수 있다.

:

\begin{align}P_2 &= \int_0^1 \frac{2\theta(x)}{\pi}\,dx \\[6px]&= \frac{2}{\pi}\int_0^1 \cos^{-1}(x)\,dx \\[6px]&= \frac{2}{\pi}\cdot 1 = \frac{2}{\pi}.\end{align}

두 결과를 곱하면 위와 같이 P = P₁ · P₂ =

\frac{l}{t} \cdot \frac{2}{\pi} = \frac{2l}{t\pi}

가 된다.

"짧은 바늘 경우"를 계산하는 훨씬 더 우아하고 간단한 방법이 있다. 영역을 경계로 하는 두 선 중 하나에서 가장 멀리 떨어진 바늘의 끝은 바늘이 이를 교차하기 위해 이 선에서 l cos θ (여기서 θ는 바늘과 수평선 사이의 각도임)의 수평 거리(경계선에 수직) 내에 위치해야 한다. 이 바늘 끝이 이 선에서 수평으로 이동할 수 있는 가장 먼 거리는 t이다. 바늘의 가장 먼 끝이 선에서 l cos θ 이하의 거리에 위치할 확률(따라서 바늘이 선을 교차할 확률)은 0 ≤ θ ≤

\frac{\pi}{2}

에 대해 바늘이 해당 영역에서 이동할 수 있는 총 거리 t에서

:

\begin{align}P &= \frac{\displaystyle\int_0^\frac{\pi}{2} l\cos\theta \, d\theta}{\displaystyle\int_0^\frac{\pi}{2} t \, d\theta} \\[6px]&= \frac l t\cdot\frac{\displaystyle\int_0^\frac{\pi}{2} \cos\theta \, d\theta}{\displaystyle\int_0^\frac{\pi}{2} d\theta} \\[6px]&= \frac l t\cdot\frac{1}{\,\frac{\pi}{2}\,} \\[6px]&=\frac{2l}{t\pi}.\end{align}

이 문제를 수학적으로 표현하면 다음과 같다. 길이

l

의 바늘을 간격

t

로 평행선이 그려진 바닥에 떨어뜨렸을 때, 선과 바늘이 교차할 확률은 얼마인가?

바늘의 중심에서 가까운 쪽 선까지의 거리를

x

라 하고, 바늘과 선이 이루는 각의 작은 쪽을

\theta

라고 한다.

0

부터

\frac{t}{2}

에서의

x

의 확률 밀도 함수는

:

\begin{cases}\frac{2}{t} &:\ 0 \le x \le \frac{t}{2}\\0 &: \text{elsewhere.}\end{cases}

이다.

또한,

0

부터

\frac{\pi}{2}

에서의

\theta

의 확률 밀도 함수는

:

\begin{cases}\frac{2}{\pi} &:\ 0 \le \theta \le \frac{\pi}{2}\\0 &: \text{elsewhere.}\end{cases}

이다.

두 확률 변수

x

와

\theta

는 독립적이므로, 결합 확률 밀도 함수는 곱하여

:

\begin{cases}\frac{4}{t\pi} &:\ 0 \le x \le \frac{t}{2}, \ 0 \le \theta \le \frac{\pi}{2}\\0 &: \text{elsewhere.}\end{cases}

가 된다.

바늘과 선이 교차하는 것은

:

x \le \frac{l}{2}\sin\theta.

일 때이다.

4. 적분 없이 해결 (짧은 바늘)

짧은 바늘 문제는 적분 없이도 해결할 수 있다. 지름이 인 원이 거리 의 띠를 항상 정확히 두 지점에서 교차한다는 기하학적 사실로부터 확률 에 대한 공식을 설명하는 방식으로 해결할 수 있다(즉, 확률 1). 이 해법은 1860년 조제프에밀 바르비에에 의해 제시되었으며^[5], "뷔퐁의 국수"라고도 불린다.

5. 라플라스의 확장

평면이 서로 직교하는 두 집합의 평행선을 포함하여 표준 수직 격자를 만드는 경우를 생각해보자. 이때 바늘이 격자에서 적어도 하나의 선과 교차할 확률을 구하는 것이 목표이다. a^영어와 b^영어를 바늘의 길이가 l^영어이고 바늘의 중간점을 포함하는 직사각형의 변이라고 하자. 짧은 바늘의 경우, 즉 l^영어 < a^영어, l^영어 < b^영어이다. (x,y)^영어를 바늘의 중간점의 좌표로, φ^영어를 바늘과 x^영어-축이 이루는 각도로 표시하자. 앞서 설명한 예와 비슷하게, x^영어, y^영어, φ^영어는 범위 0 ≤ x ≤ a^영어, 0 ≤ y ≤ b^영어, −π/2 ≤ φ ≤ π/2^영어에서 독립적인 균일한 확률 변수라고 가정한다.

이 문제를 풀기 위해, 먼저 바늘이 선과 교차하지 않을 확률을 계산한 다음, 그 여집합을 구한다. 바늘이 선과 교차하지 않는 영역의 부피를 결정하고 이를 모든 가능성의 부피 V^영어로 나누어 이 첫 번째 확률을 계산한다. V = πab^영어임을 쉽게 알 수 있다.

이제 V*^영어를 바늘이 어떤 선과도 교차하지 않는 가능성의 부피라고 하자. J.V. 우스펜스키에 의해 개발되었다.^[9]

V*^영어 = ∫-π/2π/2 F(φ)dφ^영어

여기서 F(φ)^영어는 각도 φ^영어가 주어졌을 때 바늘이 어떤 선과도 교차하지 않는 영역이다. F(φ)^영어를 결정하기 위해, 먼저 경계 직사각형의 가로 가장자리의 경우를 살펴보자. 총 변의 길이는 a^영어이고, 중간점은 가장자리의 어느 쪽 끝점에서도 l/2 cos φ^영어 이내에 있어서는 안 된다. 따라서 교차가 없는 총 허용 길이는 a − 2(l/2 cos φ)^영어 또는 a − l cos φ^영어이다. 마찬가지로, 길이가 b^영어인 세로 가장자리의 경우, b ± l sin φ^영어를 갖는다. ±는 φ^영어가 양수 또는 음수인 경우를 고려한다. 양의 경우를 취한 다음 일반성을 위해 최종 답변에 절대값 기호를 추가하면 다음과 같다.

F(φ) = (a - lcosφ)(b - lsinφ) = ab - bl cos φ - al|sin φ|+ 1/2l2|sin 2φ|.^영어

이제 다음 적분을 계산할 수 있다.

V*^영어 = ∫-π/2π/2 F(φ)dφ^영어 = πab-2bl-2al+l2^영어

따라서 바늘이 어떤 선과도 교차하지 않을 확률은 다음과 같다.

V*/V= (πab-2bl-2al+l2)/πab = 1 - (2l(a+b)-l2)/πab.^영어

마지막으로, 바늘이 적어도 하나의 선과 교차할 확률 P^영어를 계산하려면, 위 결과를 1에서 빼서 보수를 계산해야 하며, 이는 다음을 산출한다.

P = (2l(a+b)-l2)/πab^영어

6. 원주율(π) 추정

뷔퐁의 바늘 문제를 이용하면 원주율(π) 값을 추정할 수 있다. 바늘을 떨어뜨려 바늘과 선이 교차하는 확률을 계산하고, 이 확률을 이용하여 π 값을 근사하는 방식이다.^[6]

바늘의 길이 *l*이 선 사이의 간격 *t*보다 짧거나 같은 경우(즉, *l* ≤ *t*), 바늘이 선과 교차할 확률 *P*는 다음과 같다.

: $P = \frac{2l}{t\pi}.$

이 식을 π에 대해 정리하면 다음과 같다.

: $\pi = \frac{2l}{tP}.$

따라서 바늘을 여러 번 떨어뜨리는 실험을 통해 *P* 값을 추정하면, π 값 또한 추정할 수 있다.

실험에서 총 *n*번 바늘을 떨어뜨렸고, 그중 *h*번 바늘이 선과 교차했다고 가정하면, *P*는 *h/n*으로 근사된다. 이를 위 식에 대입하면 π의 근사값을 얻을 수 있다.

: $\pi \approx \frac{2l\cdot n}{t h}.$

예를 들어,

에서처럼 9칸 길이의 성냥개비를 9칸 너비의 선 사이에서 17번 던졌을 때, 11개의 성냥개비가 선을 가로질렀다면, π ≈ (2 × 9 × 17) / (9 × 11) ≈ 3.1이 된다.

에서 볼 수 있듯이, 던진 횟수가 많아질수록 계산된 π 값은 3.14에 가까워진다.

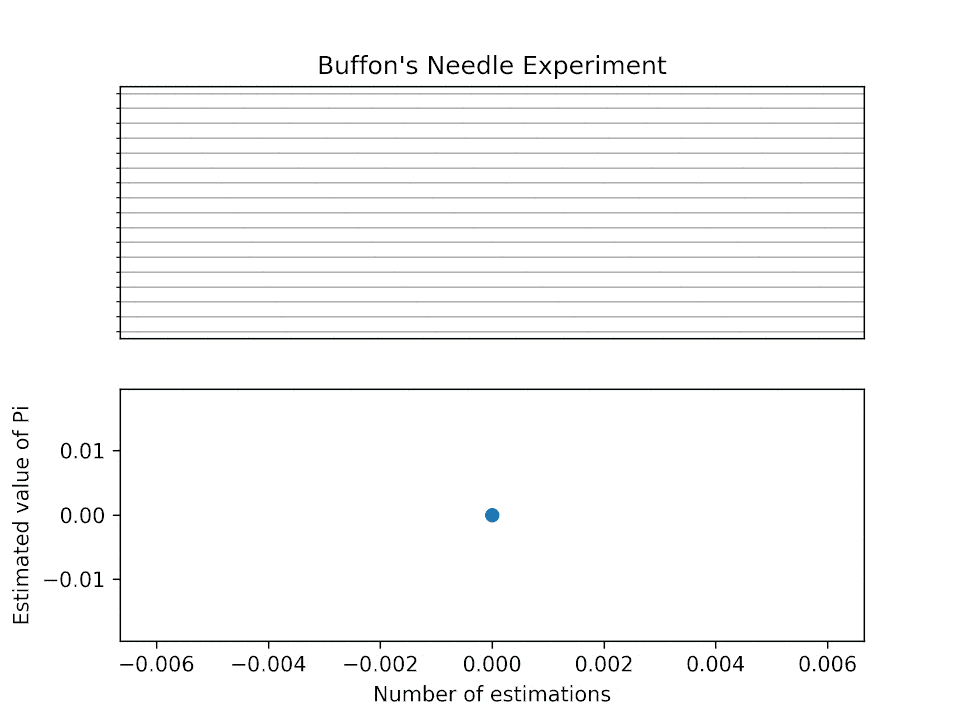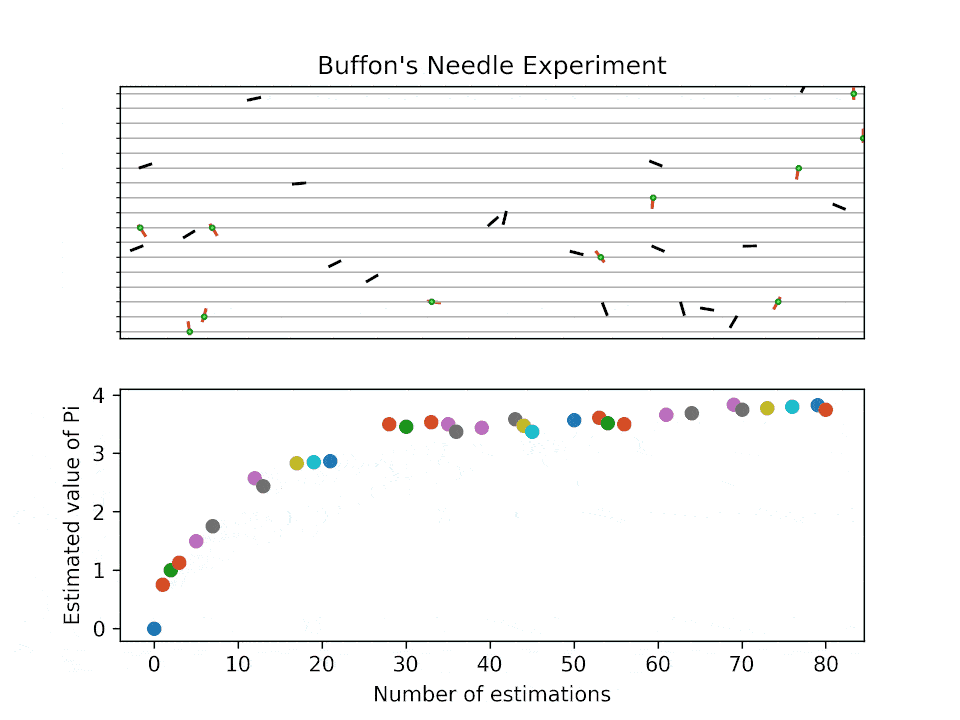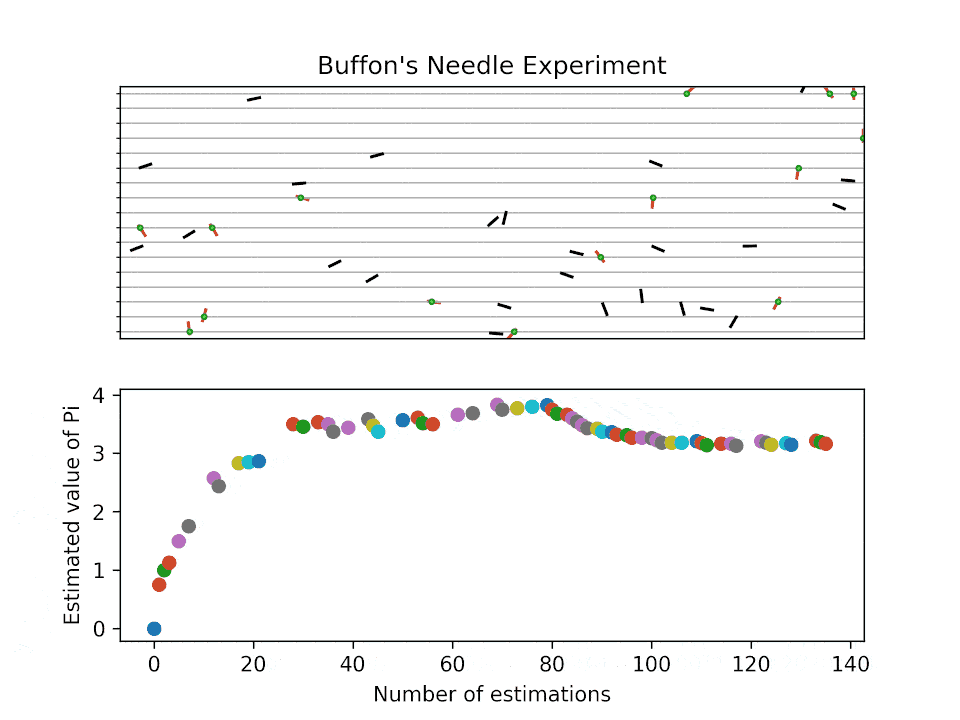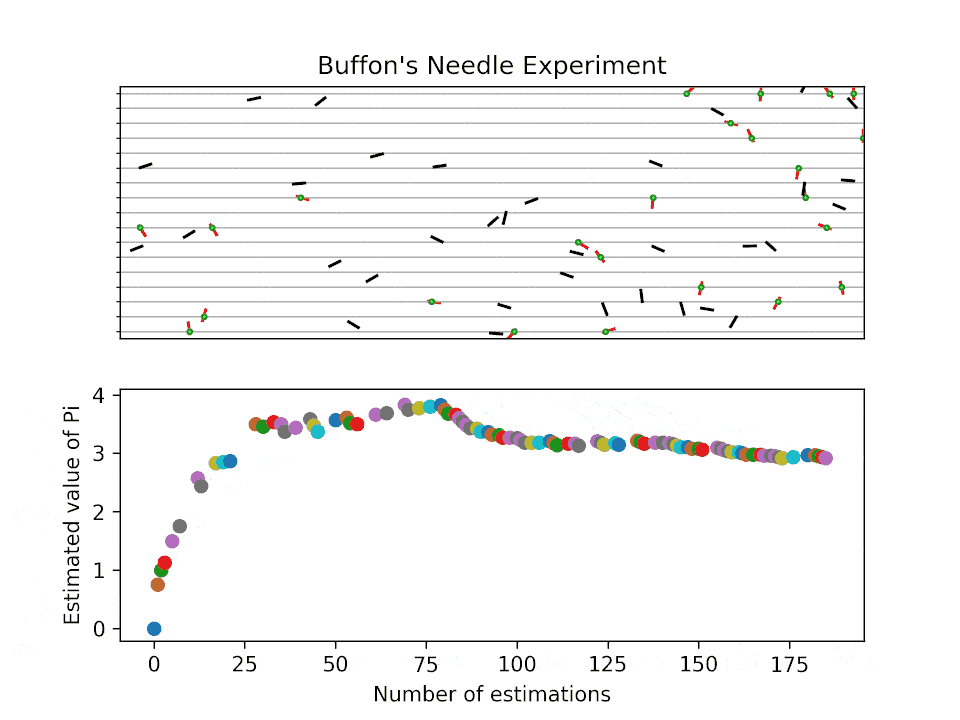
1901년 이탈리아의 수학자 마리오 라차리니는 뷔퐁의 바늘 실험을 수행하여 π 근사값으로 355/113을 얻었는데, 이는 소수점 여섯 자리까지 정확한 값이다.^[6] 그러나 라차리니의 실험은 이미 알려진 355/113이라는 근사값을 얻기 위해 의도적으로 조작되었을 가능성이 있다는 비판을 받는다.^[7] 라차리니는 바늘 길이를 선 간격의 5/6로 설정하여 실험을 진행했는데, 이 경우 π ≈ (5/3) × (n/x) (*n*은 던진 횟수, *x*는 교차 횟수)로 계산된다. 라차리니는 3,408번 (213 × 16)의 시도를 통해 결과를 얻었다.^[8]

뷔퐁의 바늘 실험과 유사한 라플라스의 실험 중 어떤 것이 π 값을 더 잘 추정하는지에 대한 연구도 진행되었다.^[10] 결론적으로, 라플라스 실험 방식이 동일한 수준의 정확도를 얻기 위해 더 적은 횟수의 실험을 필요로 한다는 것이 밝혀졌다.

7. 라차리니의 실험

1901년 이탈리아의 수학자 마리오 라자리니는 뷔퐁의 바늘 실험을 수행했다. 3,408번 바늘을 던져 π의 근사값 355/113을 얻었는데, 이는 소수점 여섯 자리까지 정확했다.^[6]

라차리니의 "실험"은 이미 잘 알려진 355/113 근사값을 재현하기 위해 설정되었으므로(실제로 분자와 분모에 5자리 미만의 숫자가 있는 더 나은 유리 근사값은 없다. 밀뤼 참조), 시도 횟수에서 예상되는 것보다 더 정확한 π의 "예측"을 얻는 확증 편향의 예이다.^[7]

라차리니는 바늘의 길이가 나무 조각 너비의 5/6인 바늘을 선택했다. 이 경우 바늘이 선을 교차할 확률은 5/(3π)이다. 따라서 n개의 바늘을 떨어뜨리고 x개의 교차를 얻으면, π를 다음과 같이 추정한다.

: $\pi \approx \frac 53 \cdot \frac nx$

라차리니가 355/113 결과를 목표로 했다면, 다음과 같은 n과 x가 필요했을 것이다.

: $\frac{355}{113} = \frac 53 \cdot \frac nx,$

또는

: $x = \frac{113 n}{213}.$

이렇게 하려면 n을 213의 배수로 선택해야 한다. 그래야 113n/213이 정수가 되기 때문이다. 그런 다음 n개의 바늘을 떨어뜨리고 정확히 x번 성공하기를 바란다. 213개의 바늘을 떨어뜨리고 113번 성공하면, 소수점 6자리까지 정확한 π의 추정값을 얻을 수 있다. 그렇지 않으면 213번 더 시도하고 총 226번의 성공을 바란다. 라차리니는 3408 = 213 × 16번의 시도를 수행하여, π의 근사값을 얻었다.

위의 설명은 라차리니에게 관대하게 여겨질 수도 있다. 중간 결과에 대한 통계 분석은, 그가 더 적은 수의 던지기에 대해 보고한 결과가 실험 전체에서 예상 값과 매우 일치할 확률이 매우 낮다는 것을 보여준다. 이 때문에 "실험" 자체가 실제로 수행되지 않았을 가능성이 매우 높지만, 통계적 기대치에 맞춰 상상력에서 만들어진 숫자들을 기반으로 했지만, 결과적으로 너무 잘 맞아 떨어졌다.^[7]

그러나 네덜란드 과학 저널리스트 한스 판 마넨은 라차리니의 기사가 잡지 독자들(교사를 대상으로 함)이 라차리니가 만들었다고 말한 장치가 설명된 대로 작동할 수 없다는 것을 분명히 알 수 있었을 것이기 때문에, 너무 진지하게 받아들여질 의도가 아니었다고 주장한다.^[8]

8. 시뮬레이션

뷔퐁의 바늘 문제는 몬테카를로 방법을 사용하여 시뮬레이션을 통해 원주율의 근사값을 구할 수 있다. 바늘을 $n$ 회 떨어뜨렸을 때 바늘과 선이 $h$ 회 교차했다면, 다음 식이 성립한다.

: $\frac{h}{n} \sim \frac{2 l}{t\pi},$

따라서 $\pi$ 는 다음과 같이 근사할 수 있다.

: $\pi \sim \frac{2{l}n}{th}.$

8. 1. 시뮬레이션 시 주의사항: 의존성 문제

이 실험을 컴퓨터로 시뮬레이션하여 원주율의 근사값을 구할 때, 0에서

\pi/2

까지의 균등 분포를 사용하여

\theta

를 결정하면 (구하려는 값인) 원주율 값에 대한 의존성이 발생한다. 의존성을 회피하려면, 다음의 의사 코드와 같이 단위 원 내부의 점을 무작위로 선택하여 원주율을 사용하지 않고

\sin \theta

의 값을 구하면 된다^[11]。

```

function simulation(l, t, n)

h = 0

for (iter = 0; iter < n; iter++)

x = Uniform(0, t/2)

repeat

dx = Uniform(0, 1)

dy = Uniform(0, 1)

radius = sqrt(dx*dx + dy*dy)

until radius <= 1

if x <= (l/2) * (dy/radius)

h = h + 1

return 2*l*n / (t*h)

```

여기서 ''Uniform(a, b)''는 a부터 b까지의 균등 난수를 나타낸다. 또한, 의사 코드에서는 편의상 예외 처리를 생략했다.

참조

_[1] 서적 Histoire de l'Acad. Roy. des. Sciences https://books.google[...] 1733
_[1] 서적 Histoire naturelle, générale et particulière https://books.google[...] 1777
_[2] 논문 Nineteenth-Century Developments in Geometric Probability: J. J. Sylvester, M. W. Crofton, J.-É. Barbier, and J. Bertrand https://www.jstor.or[...] 2001
_[3] 웹사이트 Buffon: Hat er Stöckchen geworfen oder hat er nicht? https://www.mathemat[...] 2015-03-14
_[4] 문서 The problem formulation here avoids having to work with [[Regular conditional probability|Regular conditional probability densities]].
_[5] 서적 Proofs from THE BOOK Springer Science & Business Media
_[6] 논문 Un'applicazione del calcolo della probabilità alla ricerca sperimentale di un valore approssimato di {{pi}} https://books.google[...] 1901
_[7] 간행물 Lazzarini's Lucky Approximation of {{pi}} http://www.maa.org/s[...] Mathematics Magazine 1994
_[8] 간행물 Het stokje van Lazzarini' (Lazzarini's stick) https://skepsis.nl/l[...] Skepter 2018
_[9] 서적 Introduction to Mathematical Probability https://ia601407.us.[...] 1937
_[10] 간행물 Buffon's Needle Experiment https://www.jstor.or[...] The American Mathematical Monthly 1974
_[11] 웹사이트 Lecture 10: The Alpha and the Omega of Monte Carlo https://www.coursera[...] 2017-12-13
_[12] 서적 Histoire de l'Acad. Roy. des. Sciences 1733
_[12] 서적 Histoire naturelle, générale et particulière 1777
_[13] 웹인용 Buffon: Hat er Stöckchen geworfen oder hat er nicht? https://www.mathemat[...] 2015-03-14

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com