서로소 집합 자료 구조

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 표현
- 3.1. 서로소 집합 연결 리스트 (Disjoint-set linked lists)
- 3.2. 서로소 집합 숲 (Disjoint-set forest)
4. 연산
5. 시간 복잡도
6. 응용
7. 삭제
참조

1. 개요

서로소 집합 자료 구조는 여러 개의 집합으로 분할된 원소들을 관리하는 데 사용되는 자료 구조이다. 1964년 갤러와 피셔에 의해 처음 고안되었으며, 연결 리스트와 트리 구조를 활용하여 구현될 수 있다. 주요 연산으로는 MakeSet, Find, Union이 있으며, 랭크를 이용한 유니온과 경로 압축 기법을 통해 Find와 Union 연산의 효율성을 향상시킬 수 있다. 시간 복잡도는 구현 방식에 따라 다르며, 랭크를 이용한 유니온과 경로 압축을 사용하면 각 연산에 대해 거의 상수 시간에 가까운 성능을 낼 수 있다. 서로소 집합 자료 구조는 그래프의 연결 요소 관리, 최소 신장 트리 탐색 등 다양한 알고리즘과 문제 해결에 활용된다.

더 읽어볼만한 페이지

분할 상환 자료 구조 - 스플레이 트리
스플레이 트리는 스플레이 연산을 통해 자가 균형을 유지하며 최근 접근 노드의 빠른 접근을 가능하게 하는 이진 탐색 트리로, 분할 상환 분석 시 평균적으로 O(log n)의 시간 복잡도를 가진다.
분할 상환 자료 구조 - 피보나치 힙
피보나치 힙은 최소 힙 속성을 가진 트리들의 집합으로, 각 노드의 차수를 특정 로그 값 이하로 유지하여 효율적인 삽입, 병합, 최소값 검색 연산을 지원하며, 다익스트라 알고리즘과 같은 그래프 알고리즘의 성능 향상에 활용된다.
자료 구조 - 라우팅 테이블
라우팅 테이블은 네트워크에서 데이터 전송 시 최적 경로를 결정하는 핵심 데이터베이스로, 라우터가 목적지 IP 주소를 기반으로 다음 홉을 결정하며 직접 연결 및 원격 네트워크 경로 정보를 저장하고 동적 라우팅 또는 수동 설정으로 관리된다.
자료 구조 - 스택
스택은 후입선출(LIFO) 원칙에 따라 데이터를 관리하는 추상 자료형으로, push 연산으로 데이터를 쌓고 pop 연산으로 가장 최근 데이터를 제거하며, 서브루틴 호출 관리, 수식 평가, 백트래킹 등에 활용된다.
검색 알고리즘 - 유전 알고리즘
유전 알고리즘은 생물 진화 과정을 모방하여 최적해를 탐색하는 계산 최적화 기법으로, 해를 유전자로 표현하고 적합도 함수를 통해 평가하며 선택, 교차, 돌연변이 연산을 반복하여 최적해에 근접하는 해를 생성하며, 성능은 매개변수에 영향을 받고 초기 수렴 문제 해결을 위한 다양한 변형 기법과 관련 기법이 존재한다.
검색 알고리즘 - 역색인
역색인은 단어와 해당 단어가 포함된 문서 간의 관계를 나타내는 자료 구조이며, 검색 엔진의 쿼리 속도를 최적화하는 데 사용된다.

서로소 집합 자료 구조
개요
종류	자료 구조
구조	다방향 트리
고안자	버나드 A. 갤러와 마이클 J. 피셔
고안 연도	1964년
성능
연산
설명	은 연산의 수, 은 요소의 수, 은 애커만 함수의 역함수

2. 역사

서로소 집합 자료 구조는 1964년 버나드 A. 갤러와 마이클 J. 피셔에 의해 처음 기술되었다.^[2] 1973년, 존 홉크로프트와 제프리 울만은 시간 복잡도를 $n$ 의 반복 로그인 $O(\log^{*}(n))$ 으로 제한했다.^[3]

1975년, 로버트 타잔은 알고리즘의 시간 복잡도에 대한 $O(m\alpha(n))$ (역 아커만 함수) 상한을 처음으로 증명했으며, 이 상한이 빡빡하다는 것을 증명했다. 1979년, 그는 이것이 갤러-피셔 구조를 포함하는 특정 종류의 알고리즘에 대한 하한임을 보였다.^[4]^[5]

1989년, 마이클 프레드먼과 삭스는 모든 분리 집합 자료 구조에 의해 연산당 $\Omega(\alpha(n))$ (분할 상환) $O(\log n)$ 비트의 단어가 접근되어야 함을 보였으며,^[6] 이로써 이 모델에서 자료 구조의 최적성을 증명했다.

1991년, 갈릴과 이탈리아노는 분리 집합을 위한 자료 구조에 대한 조사를 발표했다.^[7]

1994년, 리처드 J. 앤더슨과 헤더 울은 블로킹이 필요하지 않은 Union-Find의 병렬화된 버전을 설명했다.^[8]

2007년, 실뱅 콩숑과 장-크리스토프 필리아트르는 분리 집합 숲 자료 구조의 반영구적 버전을 개발하고, 증명 보조자 Coq를 사용하여 그 정확성을 공식화했다. "반영구적"은 자료 구조의 이전 버전이 효율적으로 유지되지만, 자료 구조의 이전 버전에 접근하면 이후 버전이 무효화됨을 의미한다. 그들의 가장 빠른 구현은 비영구적 알고리즘과 거의 동일한 효율성을 달성한다. 그들은 복잡성 분석을 수행하지 않았다.^[9]

특정 종류의 문제에 대해 더 나은 성능을 보이는 분리 집합 자료 구조의 변형도 고려되었다. 가보우와 타잔은 가능한 합병이 특정 방식으로 제한되면, 진정한 선형 시간 알고리즘이 가능함을 보였다.^[10]

3. 표현

서로소 집합 자료 구조는 일반적으로 연결 리스트 또는 트리(서로소 집합 숲)를 이용하여 구현된다.

숲의 노드는 응용 프로그램에 편리한 방식으로 저장할 수 있지만, 일반적인 기술은 배열에 저장하는 것이다. 이 경우 부모는 배열 인덱스로 표시할 수 있다. 각 배열 항목에는 부모 포인터에 대해 Θ(log ''n'') 비트의 저장 공간이 필요하다. 항목의 나머지 부분에 대해서도 이와 비슷하거나 적은 양의 저장 공간이 필요하므로 숲을 저장하는 데 필요한 비트 수는 Θ(''n'' log ''n'')이다. 구현에서 고정 크기 노드를 사용하는 경우(따라서 저장할 수 있는 숲의 최대 크기를 제한), 필요한 저장 공간은 n에 대해 선형이다.

서로소 집합 숲의 각 노드는 포인터와 크기 또는 랭크(둘 다는 아님)와 같은 보조 정보로 구성된다. 포인터는 각 노드가 트리의 루트가 아닌 경우 부모를 가리키는 부모 포인터 트리를 만드는 데 사용된다. 루트 노드를 다른 노드와 구별하기 위해 부모 포인터는 노드에 대한 순환 참조 또는 센티넬 값과 같은 잘못된 값을 갖는다. 각 트리는 숲에 저장된 집합을 나타내며, 집합의 구성원은 트리의 노드이다. 루트 노드는 집합 대표를 제공한다. 두 노드가 동일한 집합에 속하는 경우는 해당 노드를 포함하는 트리의 루트가 동일한 경우뿐이다.^[21]

3. 1. 서로소 집합 연결 리스트 (Disjoint-set linked lists)

서로소 집합 데이터 구조는 각 집합을 연결 리스트로 표현할 수 있다. 각 리스트의 헤드(head)는 해당 집합의 대표 원소를 저장한다.

`MakeSet`은 원소 하나만을 가지는 리스트를 생성한다. `Union`은 두 리스트를 연결하는 연산으로, 한 리스트의 헤드를 다른 리스트의 꼬리에 연결하여 상수 시간에 수행할 수 있다. `Find` 연산은 특정 원소에서부터 리스트의 헤드까지 거슬러 올라가야 하므로, 선형 시간(O(n))이 소요된다.^[26]

이러한 단점은 각 노드에 헤드를 가리키는 포인터를 추가하여 해결할 수 있다. 이 포인터를 통해 대표 원소를 바로 참조할 수 있으므로, `Find` 연산은 상수 시간에 수행된다. 그러나 `Union` 연산 시 덧붙여지는 리스트의 모든 원소의 포인터를 갱신해야 하므로 O(n) 시간이 걸린다.^[26]

각 리스트의 길이를 추적하여, 짧은 리스트를 긴 리스트에 덧붙이는 가중치 유니온 휴리스틱(weighted-union heuristic)을 사용하면 성능을 향상시킬 수 있다. 이 방법을 사용하면, n개의 원소에 대해 m개의 `MakeSet`, `Union`, `Find` 연산을 수행하는 데 O(m + n log n) 시간이 걸린다.^[26]
가중치 유니온 휴리스틱의 시간 복잡도 분석여러 리스트가 있고, 각 리스트의 노드는 속한 리스트의 이름과 원소 개수 정보를 저장한다고 가정한다. 모든 리스트의 전체 원소 개수가 n개일 때, 두 리스트를 병합하고 각 노드의 리스트 이름을 갱신하는 과정을 생각해 보자. 리스트 A의 길이가 리스트 B보다 길 경우, B의 원소들을 A에 병합하고 B에 속했던 원소들의 정보를 갱신한다.

특정 원소 x가 속한 리스트의 이름을 갱신하는 횟수를 최악의 경우에 대해 계산해 보자. x는 자신이 속한 리스트보다 길이가 같거나 긴 리스트와 병합될 때마다 리스트 이름을 갱신한다. 갱신이 일어날 때마다 x가 속한 리스트의 크기는 최소 두 배 이상 증가한다. 따라서 "크기가 n이 되기 전에 숫자가 얼마나 자주 두 배가 될 수 있는가?"라는 질문을 할 수 있고, 답은

\log_2(n)

이다. 즉, 특정 원소는 최악의 경우

\log_2(n)

번 갱신된다. 그러므로 n개의 원소를 가지는 리스트는 최악의 경우

O(n \log(n))

시간이 걸린다. 이 구조에서 각 노드는 원소가 속한 리스트의 이름을 포함하므로, `Find` 연산은

O(1)

시간이 걸린다.

이러한 분석은 이진 힙, 피보나치 힙 등의 자료 구조에서 여러 연산의 시간을 분석하는 데에도 활용된다.

3. 2. 서로소 집합 숲 (Disjoint-set forest)

서로소 집합 숲(Disjoint-set forest)은 각 집합을 트리로 표현하는 자료 구조이며, 각 노드는 부모 노드를 가리킨다. 이 구조는 1964년 버나드 A. 갤러와 마이클 J. 피셔가 처음으로 고안하였으며^[27], 이후 정밀한 분석은 수년이 걸렸다.

서로소 집합 숲에서 각 집합의 대표는 해당 트리의 루트(root) 노드이다. ''파인드''(Find) 연산은 특정 노드에서 루트 노드에 도달할 때까지 부모 노드를 따라 참조한다. ''유니온''(Union)은 두 개의 트리를 하나로 병합하는 연산으로, 한 루트 노드를 다른 루트 노드에 연결한다.

이러한 단순한 서로소 집합 숲 방법은 매우 불균형적인 트리를 생성할 수 있기 때문에, 연결 리스트 방법과 다를 바 없다.

이러한 문제를 개선하기 위해, 랭크를 이용한 유니온(Union by rank)과 경로 압축(Path compression) 기법을 사용한다.

랭크를 이용한 유니온(Union by rank): ''Union'' 연산을 수행할 때, 항상 더 낮은 랭크(rank)를 가진 트리의 루트를 더 높은 랭크를 가진 트리의 루트에 연결한다. 랭크는 트리의 높이를 나타내는 지표로 초기값은 0이며, 같은 랭크의 두 트리가 합쳐질 때만 랭크가 1 증가한다.
경로 압축(Path compression): ''Find'' 연산을 수행할 때, 방문하는 모든 노드의 부모를 루트 노드로 직접 연결하여 트리의 구조를 평탄화한다.

이 두 기법을 함께 사용하면, 각 연산의 상각 실행 시간은

O(\alpha(n))

이 된다. 여기서

\alpha(n)

은 아커만 함수의 역함수로, 실질적으로 매우 작은 상수이다.

4. 연산

서로소 집합 자료 구조는 다음 세 가지 연산을 지원한다.^[26]

MakeSet: 한 원소만을 가지는 집합을 생성한다.
유니온(Union): 두 집합을 하나의 집합으로 합친다. 연결 리스트에서는 한 리스트의 헤드가 다른 리스트의 꼬리를 가리키도록 하여 상수 시간에 연산을 수행할 수 있다.
파인드(Find): 특정 원소가 속한 집합의 대표 원소(루트 노드)를 찾는다. 연결 리스트에서는 특정 원소에서부터 리스트의 헤드까지 거꾸로 탐색해야 하므로 O(n) (선형 시간)이 걸린다.

초기에는 연결 리스트를 이용하여 구현하였는데, `Find` 연산의 시간 복잡도가 크다는 단점이 있었다. 이를 개선하기 위해 각 노드에 헤드를 가리키는 포인터를 추가하여 `Find` 연산을 상수 시간에 수행할 수 있도록 하였으나, `Union` 연산 시 덧붙여지는 모든 원소의 헤드 포인터를 갱신해야 했기 때문에 `Union` 연산이 O(n) 시간을 요구하게 되었다.

이러한 문제를 해결하기 위해 '가중치-유니온 휴리스틱'(weighted-union heuristic)을 사용할 수 있다. 이 방법은 항상 크기가 작은 리스트를 큰 리스트에 덧붙이는 방식으로, n개의 원소에 대해 m개의 MakeSet, Union, Find 연산을 수행할 경우 O(m + n log n) 시간이 걸린다.^[26]

더 빠른 연산을 위해서는 서로소 집합 숲(Disjoint-set forest)과 같은 다른 자료 구조가 필요하다. 서로소 집합 숲은 각 집합을 트리로 표현하며, 각 노드는 부모 노드를 가리킨다. 이 구조는 1964년 버나드 A. 갤러와 마이클 J. 피셔에 의해 처음 고안되었다.^[2]

파인드(Find): 특정 노드에서 시작하여 루트 노드에 도달할 때까지 부모 노드를 따라간다.
유니온(Union): 두 트리를 합치는 연산으로, 한 루트 노드를 다른 루트 노드의 자식으로 만든다.

단순한 서로소 집합 숲 구현은 불균형적인 트리가 생성될 수 있어, 연결 리스트를 사용한 방법과 성능 상 큰 차이가 없을 수 있다.

4. 1. MakeSet

'''function''' MakeSet(''x'') '''is'''

'''if''' ''x''가 이미 숲에 없다면 '''then'''

''x''.부모 := ''x''

''x''.크기 := 1 ''// 노드가 크기를 저장하는 경우''

''x''.랭크 := 0 ''// 노드가 랭크를 저장하는 경우''

'''end if'''

'''end function'''

```

이 연산은 선형 시간 복잡도를 갖는다. 특히, 개의 노드로 분리 집합 숲을 초기화하는 데는 시간이 필요하다.^[27]

노드에 부모가 할당되지 않은 것은 해당 노드가 숲에 존재하지 않음을 의미한다.

실제로는, `MakeSet`은 를 저장하기 위해 메모리를 할당하는 연산이 선행되어야 한다. 메모리 할당이 좋은 동적 배열 구현과 같이 상각된 상수 시간 연산인 한, 무작위 집합 숲의 점근적 성능을 변경하지 않는다.

분리 집합 숲에서 `MakeSet`은 노드의 부모 포인터와 노드의 크기 또는 랭크를 초기화한다. 루트가 자신을 가리키는 노드로 표현되는 경우, 요소를 추가하는 것은 위와 같은 의사 코드를 사용하여 설명할 수 있다.

4. 2. Find

Find^영어 연산은 주어진 쿼리 노드에서 루트 요소에 도달할 때까지 부모 포인터의 체인을 따라간다. 이 루트 요소는 쿼리 노드가 속한 집합을 나타내며, 쿼리 노드 자체가 될 수도 있다. Find는 도달한 루트 요소를 반환한다.^[22]

Find 연산을 수행하는 것은 숲을 개선할 수 있는 중요한 기회를 제공한다. Find 연산의 시간은 부모 포인터를 따라가는 데 소요되므로, 트리가 더 평평할수록 Find 연산이 더 빨라진다. Find가 실행될 때, 각 부모 포인터를 차례로 따라가는 것보다 루트에 더 빨리 도달하는 방법은 없다. 그러나 이 검색 중에 방문한 부모 포인터를 루트에 더 가깝게 가리키도록 업데이트할 수 있다. 루트로 가는 길에 방문한 모든 요소는 동일한 집합의 일부이므로, 이는 숲에 저장된 집합을 변경하지 않는다. 그러나 이는 쿼리 노드와 루트 사이의 노드뿐만 아니라 해당 후손에게도 향후 Find 연산을 더 빠르게 만듭니다. 이 업데이트는 분리 집합 숲의 상각된 성능 보장의 중요한 부분이다.^[22]

점근적으로 최적의 시간 복잡성을 달성하는 Find 알고리즘에는 여러 가지가 있다. '''경로 압축'''이라고 하는 일련의 알고리즘은 쿼리 노드와 루트 사이의 모든 노드가 루트를 가리키도록 한다. 경로 압축은 다음과 같이 간단한 재귀를 사용하여 구현할 수 있다.^[22]

```text

function Find(x) is

if x.parent ≠ x then

x.parent := Find(x.parent)

return x.parent

else

return x

end if

end function

```

이 구현은 트리 위로 한 번, 아래로 한 번, 두 번의 패스를 수행한다. 쿼리 노드에서 루트까지의 경로를 저장하기에 충분한 스크래치 메모리가 필요하다 (위의 의사 코드에서 경로는 호출 스택을 사용하여 암시적으로 표현된다). 이는 양방향으로 동일한 패스를 수행하여 상수 메모리 양으로 줄일 수 있다. 상수 메모리 구현은 쿼리 노드에서 루트까지 두 번 이동하며, 한 번은 루트를 찾고, 한 번은 포인터를 업데이트한다.^[22]

```text

function Find(x) is

root := x

while root.parent ≠ root do

root := root.parent

end while

while x.parent ≠ root do

parent := x.parent

x.parent := root

x := parent

end while

return root

end function

```

타잔과 판 레우엔은 최악의 경우의 복잡성은 동일하지만 실제로는 더 효율적인 단일 패스 Find 알고리즘도 개발했다.^[4] 이는 경로 분할 및 경로 반감이라고 한다. 이 둘 다 쿼리 노드와 루트 사이의 경로에 있는 노드의 부모 포인터를 업데이트한다. '''경로 분할'''은 해당 경로의 모든 부모 포인터를 노드의 조부모를 가리키는 포인터로 대체한다.^[4]

```text

function Find(x) is

while x.parent ≠ x do

(x, x.parent) := (x.parent, x.parent.parent)

end while

return x

end function

```

'''경로 반감'''은 유사하게 작동하지만 모든 두 번째 부모 포인터만 대체한다.^[4]

```text

function Find(x) is

while x.parent ≠ x do

x.parent := x.parent.parent

x := x.parent

end while

return x

end function

4. 3. Union

`Union(x, y)` 연산은 x를 포함하는 집합과 y를 포함하는 집합을 합집합으로 대체한다. `Union`은 먼저 `Find`를 사용하여 x와 y를 포함하는 트리의 루트를 결정한다. 루트가 같으면 더 이상 할 일이 없다. 그렇지 않으면 두 트리를 병합해야 한다. 이는 x의 루트의 부모 포인터를 y로 설정하거나, y의 루트의 부모 포인터를 x로 설정하여 수행된다.

어떤 노드가 부모가 될 것인지에 대한 선택은 트리에 대한 향후 연산의 복잡성에 영향을 미친다. 부주의하게 수행하면 트리가 지나치게 길어질 수 있다.

효율적인 구현에서 트리 높이는 '''크기별 합치기''' 또는 '''랭크별 합치기'''를 사용하여 제어된다. 두 전략 모두 트리가 너무 깊어지지 않도록 보장한다.

크기별 합치기(Union by size): 더 많은 자손을 가진 노드가 부모가 되도록 트리를 병합한다.
랭크별 합치기(Union by rank): 랭크(트리 높이의 상한)가 낮은 트리를 랭크가 높은 트리 아래에 붙인다.

소 집합 숲에서는 각 집합의 대표는 트리 구조의 루트가 된다. ''Union''은 두 개의 트리 구조를 하나로 합치는 연산이며, 어느 쪽의 루트가 전체의 루트가 된다. 아래에 소 집합 숲의 구현 예를 의사 코드로 나타낸다.

```

function Union(x, y)

xRoot := Find(x)

yRoot := Find(y)

xRoot.parent := yRoot

```

이러한 단순한 구현에서는 연결 리스트를 사용한 경우와 다르지 않다. 왜냐하면 트리 구조의 평형이 유지되지 않기 때문이다. 그러나 이것을 개선하는 방법이 두 가지 있다.

첫 번째 방법은 ''union by rank''라고 하며, ''Union'' 연산에서 항상 더 큰 트리가 전체의 루트가 되도록 연결하는 것이다. 트리의 크기를 평가하기 위해 ''rank''를 사용한다. 이것은 1요소의 트리의 rank를 0으로 하고, 같은 rank ''r''의 트리를 연결했을 때, 전체 루트로 한 쪽 트리의 rank를 ''r''+1로 하는 것이다. 이렇게 하는 것만으로 ''MakeSet'', ''Union'', ''Find'' 연산의 상각 실행 시간은

O(\log n)

이 된다. 개선된 `Union`의 의사 코드는 다음과 같다.

```

function Union(x, y)

xRoot := Find(x)

yRoot := Find(y)

if xRoot.rank > yRoot.rank

yRoot.parent := xRoot

else if xRoot.rank < yRoot.rank

xRoot.parent := yRoot

else if xRoot != yRoot // x 와 y 가 같은 집합에 없는 경우만 병합한다.

yRoot.parent := xRoot

xRoot.rank := xRoot.rank + 1

5. 시간 복잡도

단순한 구현(연결 리스트 또는 불균형 트리)에서는 Find 및 Union 연산에 O(n) 시간이 소요될 수 있다.^[11] 경로 압축만 사용하는 경우, n개의 MakeSet 연산, 최대 n-1개의 Union 연산, f개의 Find 연산을 수행하는 최악의 경우 실행 시간은 $\Theta(n+f \cdot \left(1 + \log_{2+f/n} n\right))$ 이다.^[11]

랭크를 이용한 유니온을 사용하고 Find 중에 부모 포인터를 갱신하지 않으면, 최대 n개의 MakeSet 연산을 포함하여 모든 유형의 m개의 연산에 대해 O(m log n)의 실행 시간을 갖는다.^[11]

랭크별 합치기와 경로 압축(또는 분할, 반감)을 함께 사용하면, m개의 연산에 대해 $O(m\alpha(n))$ 의 시간이 소요된다.^[4]^[5] (역 아커만 함수) 이는 각 연산의 상각 실행 시간을 $O(\alpha(n))$ 으로 만들며, 점근적으로 최적이다.^[6] 역 아커만 함수는 매우 느리게 증가하므로, 실질적인 n 값에 대해 4 이하의 값을 가진다. 따라서 서로소 집합 연산은 사실상 상각 상수 시간에 가깝다.

N. 블룸은 경로 압축을 사용하지 않지만 union 중에 트리를 압축하는 연산 구현을 제시했다. 그의 구현은 연산당 $O(\log n / \log\log n)$ 시간에 실행된다.^[16] 알스트럽 등은 최악 시간 복잡도 $O(\log n / \log\log n)$ 와 역 아커만 분할 상환 시간을 함께 갖는 구조를 제시했다.^[17]

6. 응용

서로소 집합 자료구조는 무향 그래프의 연결된 요소들을 추적하는 데 사용될 수 있다. 이 모델은 두 개의 꼭짓점들이 같은 요소에 속하는지 또는 그 꼭짓점들을 엣지로 연결할 때 사이클이 발생하는지 등을 결정할 수 있다. 유니온-파인드 알고리즘은 고성능 단일화 구현에 활용된다.^[29]

이 자료 구조는 Boost Graph Library에서 점진적 연결 요소([https://web.archive.org/web/20081012154946/http://boost.org/libs/graph/doc/incremental_components.html Incremental Connected Components]) 기능을 구현하는 데 활용된다. 또한 크루스칼 알고리즘에서 그래프의 최소 신장 트리를 찾는 데 활용된다.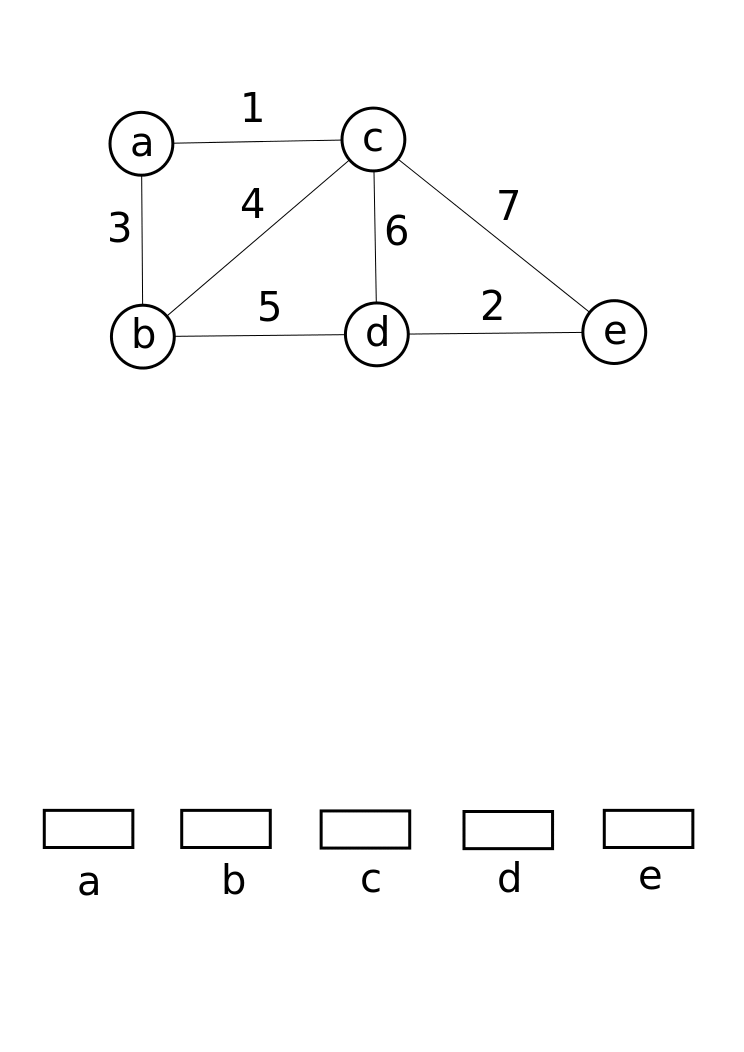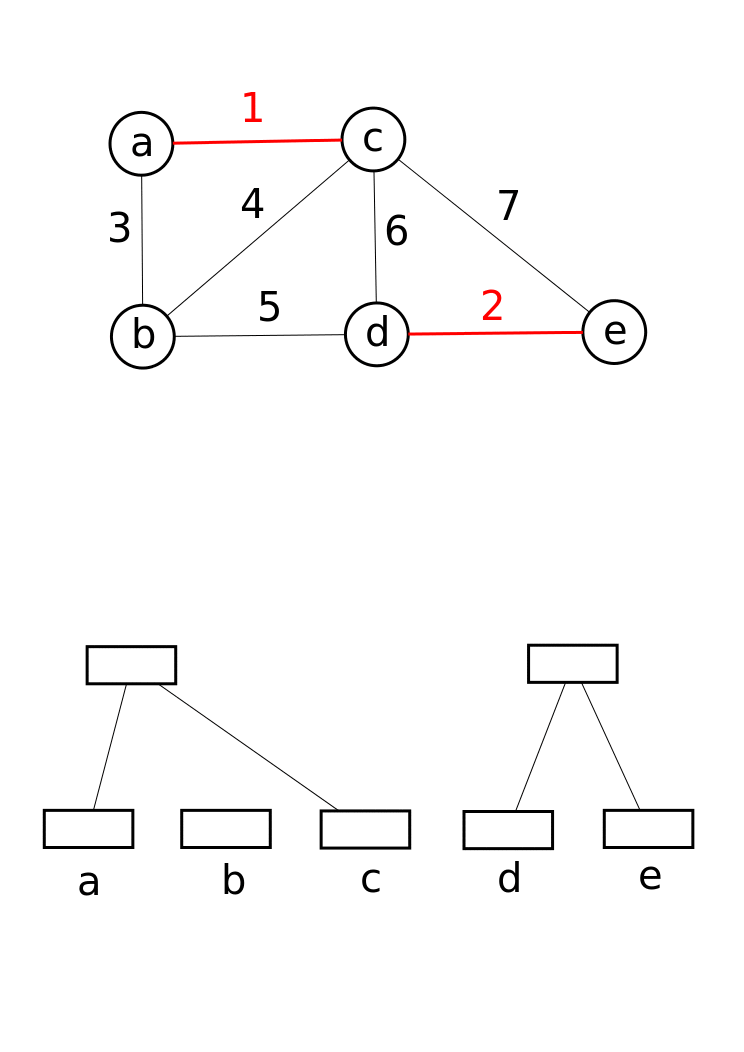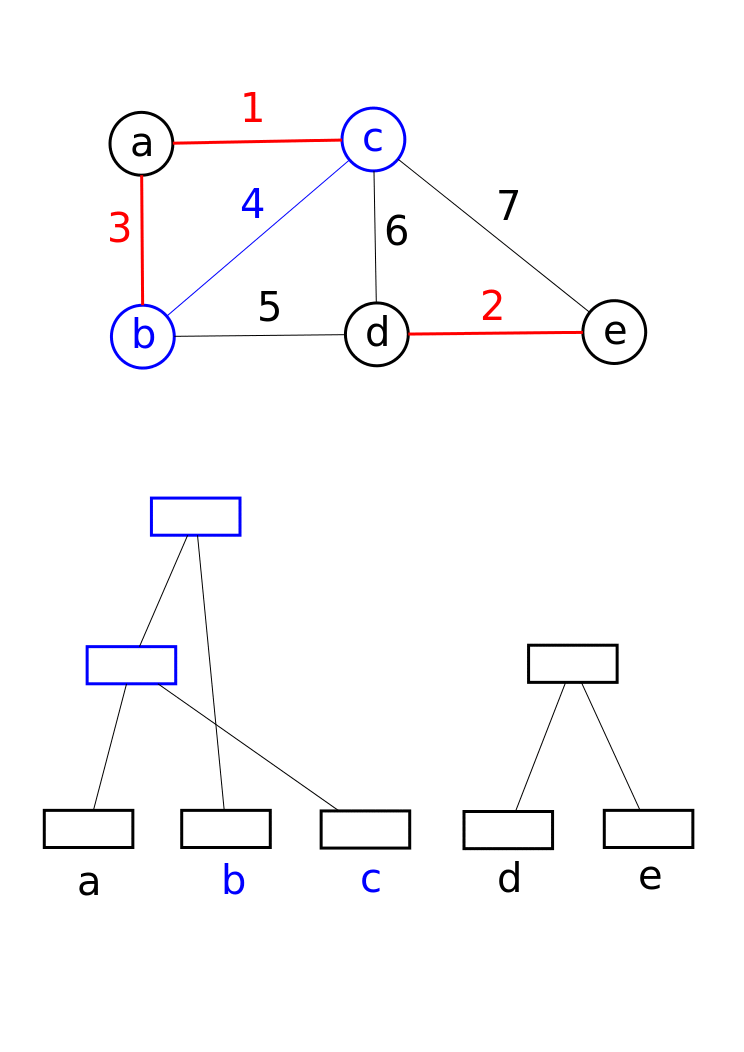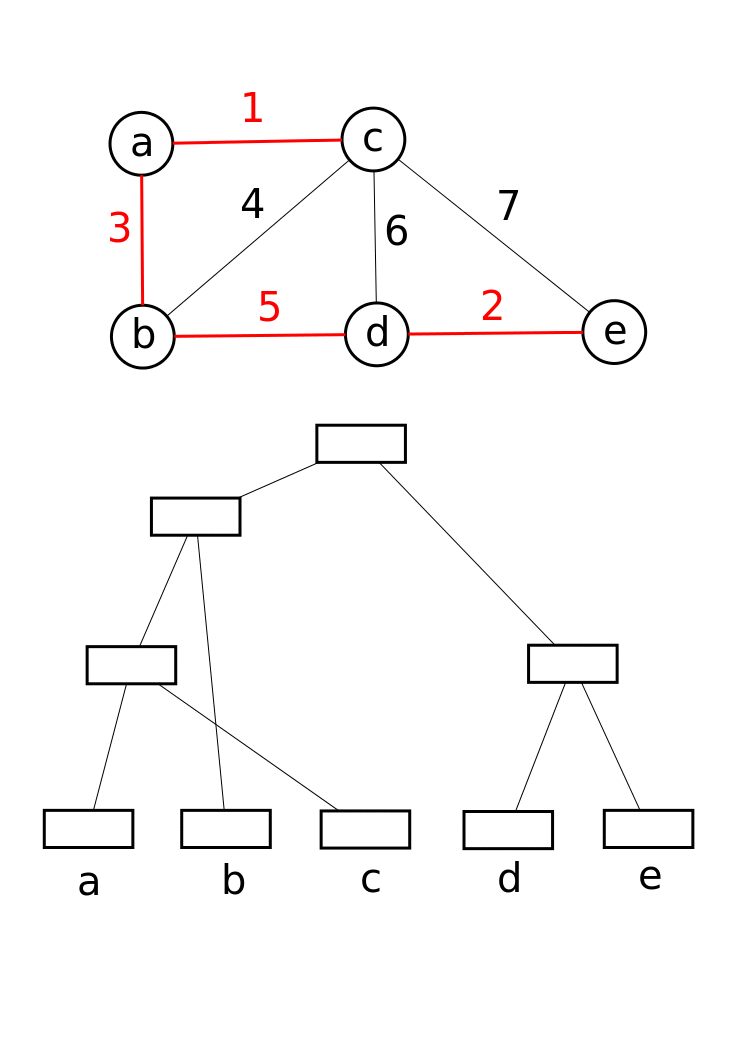

크루스칼 알고리즘을 활용하여 최소 신장 트리를 찾을 때 유니온-파인드 연산의 데모

호셴-코펠만 알고리즘은 알고리즘에서 Union-Find를 사용한다.

7. 삭제

일반적인 서로소 집합 숲 구현은 원소 삭제를 지원하지 않거나 비효율적이다. 즉, 원소의 수가 감소해도 `Find` 연산 시간은 개선되지 않는다. 하지만, 상수 시간 내 삭제를 허용하고 `Find` 연산의 시간 복잡도가 ''현재'' 원소의 수에 의존하는 현대적인 구현 방식이 존재한다.^[18]^[19]

참조

_[1] 논문 Efficiency of a Good But Not Linear Set Union Algorithm
_[2] 논문 An improved equivalence algorithm 1964-05
_[3] 논문 Set Merging Algorithms
_[4] 논문 Worst-case analysis of set union algorithms
_[5] 논문 A class of algorithms which require non-linear time to maintain disjoint sets
_[6] 서적 Proceedings of the twenty-first annual ACM symposium on Theory of computing - STOC '89 1989-05
_[7] 논문 Data structures and algorithms for disjoint set union problems
_[8] 간행물 Wait-free Parallel Algorithms for the Union-Find Problem
_[9] 간행물 ACM SIGPLAN Workshop on ML https://www.lri.fr/~[...] 2007-10
_[10] 뉴스 A linear-time algorithm for a special case of disjoint set union https://doi.org/10.1[...] 1985
_[11] 서적 Introduction to Algorithms MIT Press
_[12] 문서 Top-down analysis of path compression 2005
_[13] 논문 Efficiency of a Good But Not Linear Set Union Algorithm http://portal.acm.or[...]
_[14] 논문 Set Merging Algorithms
_[15] 문서 Worst-case analysis of set union algorithms 1984
_[16] 논문 On the Single-Operation Worst-Case Time Complexity of the Disjoint Set Union Problem 1985
_[17] 서적 Proceedings of the thirty-first annual ACM symposium on Theory of Computing 1999
_[18] 논문 Union-Find with Constant Time Deletions 2014
_[19] 논문 A simple and efficient Union-Find-Delete algorithm 2011
_[20] 논문 Unification: A multidisciplinary survey http://www.isi.edu/n[...]
_[21] 서적 Introduction to Algorithms MIT Press and McGraw-Hill 2001
_[22] 뉴스 An improved equivalence algorithm http://portal.acm.or[...] 1964-05
_[23] 간행물 The cell probe complexity of dynamic data structures 1989-05
_[24] 뉴스 Data structures and algorithms for disjoint set union problems http://portal.acm.or[...] 1991-09
_[25] 간행물 A Persistent Union-Find Data Structure 2007-10
_[26] 서적 Introduction to Algorithms MIT Press
_[27] 논문 An improved equivalence algorithm http://portal.acm.or[...] 1964-05
_[28] 간행물 The cell probe complexity of dynamic data structures 1989-05
_[29] 논문 Unification: A multidisciplinary survey http://portal.acm.or[...]
_[30] 논문 Efficiency of a Good But Not Linear Set Union Algorithm http://portal.acm.or[...]
_[31] 논문 Set Merging Algorithms
_[32] 논문 Worst-case analysis of set union algorithms
_[33] 간행물 ACM SIGPLAN Workshop on ML https://www.lri.fr/~[...] 2007-10

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com