소실점
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
소실점은 투시도법에서 평행한 선들이 시각적으로 한 점으로 모이는 지점을 의미하며, "방향점"이라고도 불린다. 이는 수학적 원리에 기반하며, 1점, 2점, 3점 투시 등 다양한 형태로 나타난다. 소실점은 예술, 건축, 디자인, 컴퓨터 그래픽스 등 다양한 분야에서 활용되며, 특히 원근감을 표현하고 공간을 시각화하는 데 중요한 역할을 한다. 또한 컴퓨터 비전 분야에서는 이미지 분석 및 3D 재구성을 위해 소실점 검출 기술이 사용된다.
더 읽어볼만한 페이지
| 소실점 | |
|---|---|
| 개요 | |
| 정의 | 평행한 선들이 무한히 멀어질 때 만나는 가상의 점 |
| 설명 | 원근법에서 3차원 공간을 2차원 평면에 표현하기 위해 사용 시각 예술과 수학에서 중요한 개념 |
| 시각 예술에서의 역할 | |
| 선형 원근법 | 모든 평행선이 단일 소실점에서 수렴하는 것으로 표현 깊이와 공간감을 나타내는 데 사용 |
| 소실점의 수 | 1점 투시, 2점 투시, 3점 투시 등 다양한 원근법 존재 소실점의 수는 그림의 복잡성과 표현 방식에 영향 |
| 주요 화가 | 레오나르도 다 빈치와 알브레히트 뒤러 등 |
 | |
 | |
| 수학에서의 응용 | |
| 투영 기하학 | 소실점은 무한대의 점으로 취급되어 기하학적 변환 연구에 활용 |
| 사영 기하학 | 사영 공간에서 평행선의 교점으로 정의 |
| 기타 | |
| 관련 용어 | 아이 포인트 시점 수평선 |
| 주의 사항 | 소실점의 위치에 따라 그림의 느낌이 크게 달라질 수 있음 |
2. 소실점의 정의 및 기본 원리
소실점은 3차원 공간의 평행한 직선들이 2차원 평면(그림, 사진 등)에 투영될 때 한 점으로 모이는 점이다. 관찰자의 시점과 평행한 직선들이 무한히 멀어졌을 때 만나는 점으로 생각할 수 있다. 소실점은 투영되는 평면(화면)과 평행하지 않은 직선들에 대해서만 존재한다. 화면과 평행한 직선들은 소실점을 가지지 않고 투시도 상에서 평행하게 표현된다.[4]
소실점은 직선에서 기원하며, 소실선은 그림면에 평행하지 않은 평면에서 기원한다. 눈의 위치와 평면에 평행하고 위에 놓인 평면이 주어지면, 평면의 '''소실선'''은 이다. 예를 들어, 평면이 지면이고 평면이 지평면일 때, 지면의 소실선은 지평선이다.
간단히 말해, 어떤 평면의 소실선은 영상 평면과 다른 평면의 교선으로 얻어진다. 이 다른 평면은 관심 있는 평면에 평행하고 카메라 중심을 통과한다. 이 평면에 평행한 여러 직선들의 각각의 소실점들은 이 소실선 위에 놓인다. 지평선은 관찰자의 눈높이를 나타내는 이론적인 선이다. 물체가 지평선 아래에 있으면, 그 물체의 선들은 지평선으로 각도를 올린다. 물체가 위에 있으면, 그 선들은 아래로 경사집니다.
직선 TL의 투시도를 그리는 경우를 생각해보자. (그림 1-1) T는 직선이 화면과 만나는 점이고, L은 무한원점이다. TL 위의 점 1을 향한 시선(점 1과 시점 E를 잇는 직선)이 화면과 만나는 점 1’은 1의 투시도이다. 1의 옆에 2, 3, 4…을 잡으면 2’, 3’, 4’…이 각각의 투시도가 된다. 무한원점 L의 투시도는 시점 E를 지나고 TL과 평행한 직선이 화면과 만나는 점 V이며, V를 직선 TL의 소실점이라고 한다.(그림 1-2)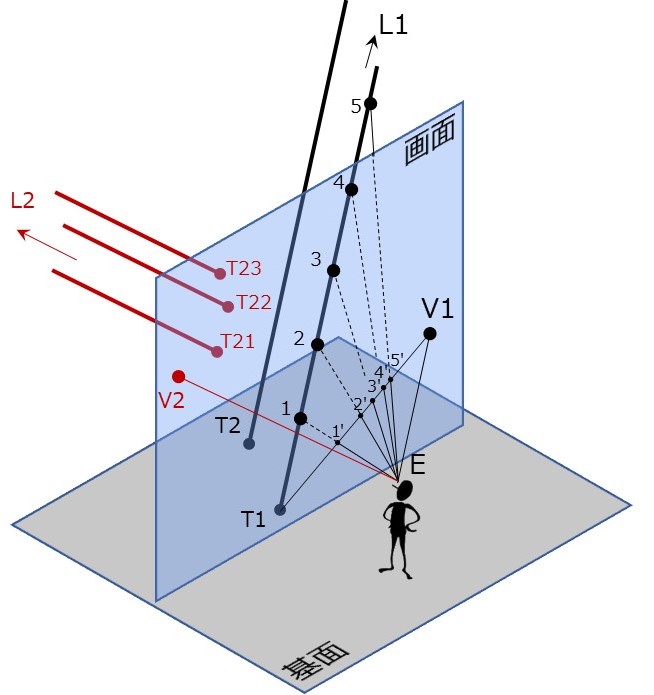
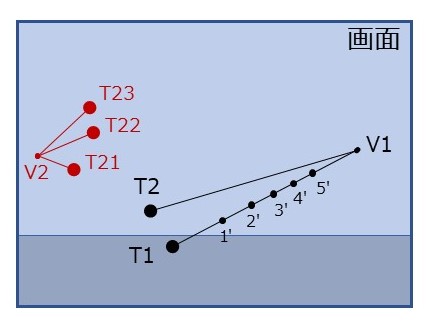
따라서 서로 평행한 직선군의 소실점은 각각 하나의 점(V1, V2, …)이 된다.(그림 2-1, 2-2) 화면과 평행한 직선군에는 소실점이 없다.
투시도로 그리는 대상은 건축물처럼 대개 직육면체 또는 그 조합으로 수직선을 포함하는 경우가 많다. 화면도 수직면으로 하는 것이 일반적이다. 이 경우, 기둥과 같은 수직선은 화면과 평행하므로 소실점이 없고, 투시도상에서는 평행한 직선군으로 그려진다. 그러나 그림 3-1과 같이 화면을 수직면에서 기울이면 기둥에도 소실점(V3)이 생긴다.(그림 3-2)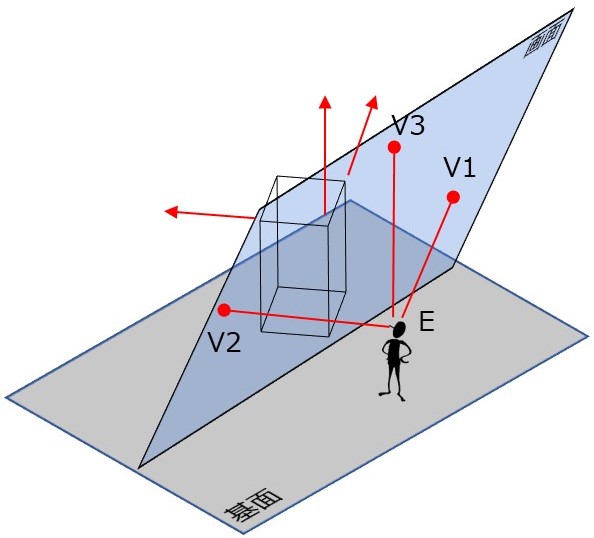
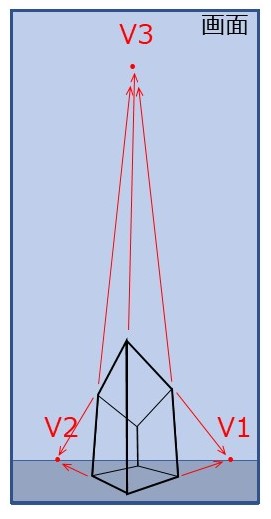
건축물 등의 완성 예상도나 준공 사진에서는 이러한 표현은 기둥이 기울어져 부자연스럽다는 이유로 피하는 경우가 있다. 하지만 내려다보는 구도에서는 화면을 기울여도 부자연스러움을 느끼지 않는 경우도 있다고 한다.
그리는 평면에 평행하고, 시점을 지나는 평면이 화면과 만나는 선을 消失線(소실선)이라고 한다. 기면의 소실선은 지평선이다。
2. 1. 벡터 표기법 (Vector notation)
소실점은 "방향점"으로도 불릴 수 있는데, 동일한 방향 벡터를 갖는 선들은 동일한 소실점을 갖기 때문이다. 수학적으로, 영상 평면 상에 있는 점 q영어 ≡ (x, y, f) (여기서 f는 카메라의 초점 거리)에 대해, vq ≡ (x/h, y/h, f/h)는 q영어와 관련된 단위 벡터이고, h = √(x2 + y2 + f2)이다. 공간에서 단위 벡터 ns ≡ (nx, ny, nz)를 갖는 직선 S와 그 소실점 vs을 고려하면, vs과 관련된 단위 벡터는 ns와 같다(두 점 모두 영상 평면을 향한다고 가정).[4]3. 소실점의 정리 및 성질
'''소실점 정리'''는 원근법 과학의 주요 정리이다. 이 정리는 그림 평면에 평행하지 않은 공간의 직선의 상(image)이 와의 교집합과 소실점에 의해 결정된다는 것을 말한다.[5] 귀도발도 델 몬테는 여러 가지 검증을 제시했고, 험프리 디튼은 이 결과를 "주요하고 위대한 명제"라고 불렀다.[5] 브룩 테일러는 1714년에 원근법에 관한 최초의 영어 책을 저술했는데, 이 책에서 "소실점"이라는 용어를 도입했고 다점 투시의 기하학을 완전히 설명한 최초의 책이었으며, 역사가 키르스티 안데르센은 이러한 관찰 결과들을 정리했다.[1] 그녀는 사영기하학의 관점에서 소실점은 과 관련된 무한원점의 상이며, 소실점을 통과하는 로부터의 시선은 에 평행하다는 점을 지적한다.
소실점이 직선에서 기원하는 것처럼, 소실선은 그림면에 평행하지 않은 평면 에서 기원한다. 눈의 위치 와 에 평행하고 위에 놓인 평면 이 주어지면, 의 '''소실선'''은 이다. 예를 들어, 가 지면이고 가 지평면일 때, 의 소실선은 지평선 이다.
간단히 말해, 어떤 평면(예: )의 소실선은 영상 평면과 다른 평면(예: )의 교선으로 얻어진다. 이 다른 평면은 관심 있는 평면()에 평행하고 카메라 중심을 통과한다. 이 평면 에 평행한 여러 직선들의 각각의 소실점들은 이 소실선 위에 놓인다. 지평선은 관찰자의 눈높이를 나타내는 이론적인 선이다. 물체가 지평선 아래에 있으면, 그 물체의 선들은 지평선으로 각도를 올린다. 물체가 위에 있으면, 그 선들은 아래로 경사집니다.
# 어떤 평면 에 놓인 두 집합의 평행선들의 투영은 수렴하는 것처럼 보이며, 즉 그 쌍과 관련된 소실점은, 이미지 평면과 에 평행하고 핀홀을 통과하는 평면의 교차로 형성된 지평선 또는 소실선 위에 나타난다.
# , , 및 가 공간에서 서로 직교하는 세 개의 직선이고, , , 가 각각 해당하는 세 개의 소실점이라고 할 때, 만약 우리가 이 점들 중 하나, 예를 들어 의 좌표와 두 번째 점, 예를 들어 을 통과하는 이미지 평면의 직선의 방향을 알고 있다면, 와 의 좌표를 모두 계산할 수 있다.[4]
# , , 및 가 공간에서 서로 직교하는 세 개의 직선이고, , , 가 각각 해당하는 세 개의 소실점이라고 할 때, 세 소실점을 꼭짓점으로 하는 삼각형의 직교중심은 광축과 이미지 평면의 교점이다.[4]
4. 투시도법의 종류
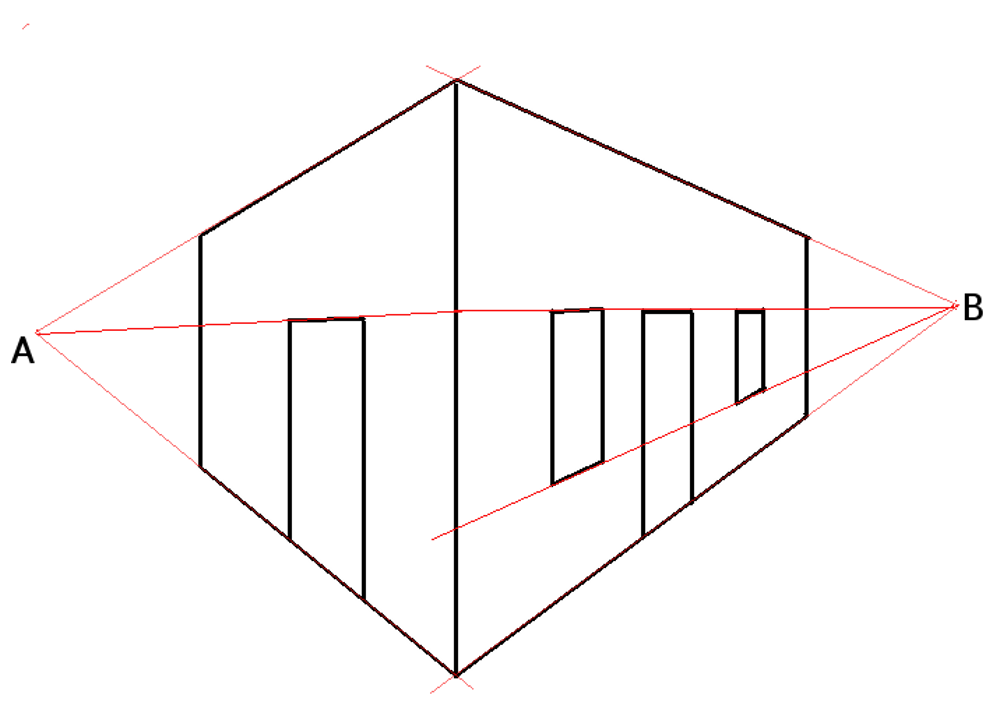
투시도법은 소실점의 개수에 따라 1점 투시, 2점 투시, 3점 투시 등으로 나뉜다.
곡선 투시(Curvilinear perspective)는 소실점이 4개 또는 5개인 그림이다. 5점 투시에서는 소실점이 원에 매핑되며, 동서남북(東西南北)의 주요 방향에 4개의 소실점이 있고 원의 중심에 하나의 소실점이 있다.
역 투시(Reverse perspective)는 그림 바깥에 소실점을 배치하여 소실점이 그림 "앞에" 있는 것처럼 보이는 그림이다.[1]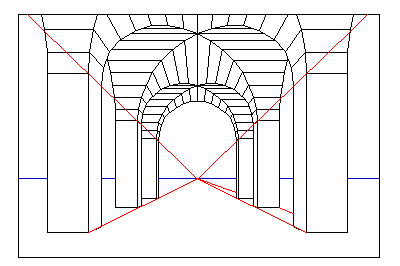
5. 소실점의 활용
소실점은 다음과 같은 다양한 분야에서 활용되고 있다.
- 카메라 보정: 영상의 소실점은 카메라 보정에 중요한 정보를 포함하고 있으며, 이를 통해 카메라의 내부 및 외부 보정 매개변수를 찾는데 사용된다.[7]
- 3차원 재구성: 인공 환경은 장면의 여러 선들이 평행하고, 여러 모서리들이 직교한다는 특징을 가지고 있다. 소실점은 이러한 환경을 이해하는 데 도움을 주며, 평면의 평행선 집합을 이용하여 평면의 방향을 계산할 수 있다. 토레(Torre)[8]와 코엘료(Coelho)[9]는 소실점을 사용하여 전체 시스템을 구현하는 데 대한 광범위한 연구를 수행했다. 이들은 장면의 단일 이미지에서 구성된 소실점을 사용하여 3차원 기하학을 복원했다.
이러한 소실점을 활용하는 아이디어는 로봇 공학, 특히 내비게이션 및 자율 주행 자동차, 그리고 객체 탐지와 관련된 분야에서도 사용된다.
5. 1. 예술 분야
회화나 일러스트레이션 등에서 소실점은 원근감을 표현하고 사실적인 공간을 묘사하는 데 사용된다. 르네상스 시대 화가들은 소실점을 활용한 원근법을 통해 깊이감 있는 공간 표현을 발전시켰다. 그 예시로, 피에트로 페루지노의 시스티나 예배당에 있는 프레스코화 ''열쇠의 인도(1481–82)가 있다.[5] 이 그림에서의 투시법 사용은 르네상스를 로마로 가져오는 데 기여했다.사진 촬영에서도 소실점은 구도와 원근감을 조절하는 데 중요한 역할을 한다.
5. 2. 건축 및 디자인 분야
건축 투시도를 작성하여 건물의 완성된 모습을 예측하고 시각화하는 데 소실점이 사용된다. 인테리어 디자인, 무대 디자인 등에서 공간을 구성하고 배치하는 데 활용된다.건축물 등의 완성 예상도(퍼스)나 준공 사진에서는 기둥이 기울어져 부자연스럽다는 이유로 이러한 표현은 피하는 경우가 있다. 하지만 내려다보는 구도에서는 화면을 기울여도 부자연스러움을 느끼지 않는 경우도 있다고 한다.

5. 3. 컴퓨터 그래픽스 및 영상 처리
컴퓨터 그래픽스와 영상 처리 분야에서 소실점은 3차원 모델링, 렌더링 등을 통해 사실적인 이미지를 만드는 데 매우 중요한 역할을 한다.- 카메라 보정: 영상 속 소실점은 카메라 보정에 필요한 정보를 제공하여, 카메라의 내부 및 외부 매개변수를 추정하는 데 사용된다.[7]
- 3차원 재구성: 소실점을 활용하여 장면의 3차원 기하학적 구조를 복원할 수 있다.[8][9]
영상에서 소실점을 찾는 방법은 여러 가지가 있는데, 영상에서 검출된 선분을 이용하거나 영상 픽셀의 강도 기울기를 직접 고려하는 방법 등이 있다.
일반적으로 영상에는 많은 소실점이 존재하기 때문에, 장면의 주요 방향에 해당하는 소실점을 찾는 것이 중요하다. 이 과정은 크게 두 단계로 나뉜다.
1. 누적 단계: 선분들을 클러스터링하여 공통 소실점을 찾는다. 이 단계에서는 누산 공간이라는 경계가 있는 공간에 영상을 매핑한다. Barnard[6]는 이 공간을 카메라의 광학 중심에 중심을 둔 가우스 구로 가정했다. 영상의 선분은 가우스 구면 상의 대원에 해당하며, 소실점은 한 점에 매핑된다. 가장 효율적인 기법 중 하나는 허프 변환을 사용하여 선분의 매개변수를 경계가 있는 공간에 매핑하는 것이다.
2. 검색 단계: 누산 공간에서 가장 많은 선분이 통과하는 셀을 찾아 주요 소실점을 결정한다.
이러한 과정을 통해 찾아낸 소실점은 인공 환경을 이해하는 데 도움을 준다. 특히, 장면의 여러 선들이 평행하고, 여러 모서리들이 직교하는 특징을 가진 환경에서 소실점은 평면의 방향을 계산하는 데 사용될 수 있다.
소실점은 로봇 공학 분야, 특히 내비게이션 및 자율 주행 자동차, 그리고 객체 탐지와 관련된 분야에서도 활용된다.
5. 4. 소실점 검출 (Detection)
영상에서 소실점을 검출하는 여러 방법은 영상에서 검출된 선분을 이용한다. 다른 기법들은 영상 픽셀의 강도 기울기를 직접 고려한다.영상에는 상당히 많은 수의 소실점이 존재한다. 따라서 목표는 장면의 주요 방향에 해당하는 소실점을 검출하는 것이다. 이는 일반적으로 두 단계로 이루어진다. 첫 번째 단계는 누적 단계(accumulation step)로, 클러스터가 공통의 소실점을 가질 것이라는 가정하에 선분들을 클러스터링한다. 다음 단계는 장면에 존재하는 주요 클러스터를 찾는 단계이므로 검색 단계(search step)라고 한다.
'''누적 단계'''에서 영상은 누산 공간(accumulator space)이라고 하는 경계가 있는 공간에 매핑된다. 누산 공간은 셀이라고 하는 단위로 분할된다. Barnard[6]는 이 공간을 누산 공간으로서 카메라의 광학 중심에 중심을 둔 가우스 구로 가정했다. 영상의 선분은 이 구면상의 대원에 해당하며, 영상의 소실점은 한 점에 매핑된다. 가우스 구는 대원이 통과할 때 증가하는 누산 셀을 가지며, 즉 영상에서 선분이 소실점과 교차한다. 그 이후로 여러 가지 수정이 이루어졌지만, 가장 효율적인 기법 중 하나는 선분의 매개변수를 경계가 있는 공간에 매핑하는 허프 변환을 사용하는 것이었다. 여러 개의 소실점에 대해서는 계단식 허프 변환이 적용되었다.
영상에서 경계가 있는 공간으로 매핑하는 과정에서 선분과 점 사이의 실제 거리가 손실된다.
'''검색 단계'''에서 선분이 통과하는 누산 셀 중 가장 많은 수의 선분을 가진 셀을 찾는다. 그런 다음 해당 선분을 제거하고, 이 횟수가 특정 임계값 이하로 떨어질 때까지 검색 단계를 반복한다. 현재 더 많은 컴퓨팅 성능이 가능해짐에 따라 서로 직교하는 두 개 또는 세 개의 방향에 해당하는 점을 찾을 수 있다.
참조
[1]
서적
Geometry of an Art
Springer
2007
[2]
학술지
Alberti's De Pictura: Its Literary Structure and Purpose
1984
[3]
잡지
TO PIERCE THE DISTANCE: Untold dimensions of the railroad vanishing point
https://railphoto-ar[...]
Center for Railroad Photography & Art
2023-06-01 # Summer 2023을 6월 1일로 가정
[4]
학술지
Using Vanishing Points for Camera Calibration
https://link.springe[...]
1990-03-01 # March 1990을 3월 1일로 가정
[5]
서적
Treatise on Perspective
1712
[6]
학술지
Interpreting Perspective Images
1983
[7]
학술대회
Metric Rectification for perspective images of planes
1998-06-01 # June 1998을 6월 1일로 가정
[8]
학술대회
Vanishing Point Calculation as a Statistical Inference on the Unit Sphere
1990-12-01 # December 1990을 12월 1일로 가정
[9]
학술대회
Using Geometrical Rules and a priori Knowledge for the Understanding of Indoor Scenes
1990-09-01 # September 1990을 9월 1일로 가정
[10]
서적
(제목 없음)
1965
[11]
서적
消点 vanishing point
2024-07-30
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
