맨위로가기

스윙바이

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

스윙바이는 우주 탐사선이 행성 등의 천체의 중력을 이용하여 궤도와 속도를 조절하는 기술이다. 1938년에 개념이 제안되었으며, 1959년 소련의 루나 3호가 달의 뒷면을 촬영하는 데 처음 사용되었다. 스윙바이는 로켓 연료를 절약하면서 우주선의 속도를 증가시키거나 감소시키는 데 활용되며, 보이저 호, 파이어니어 11호 등 주요 탐사선들이 이 기술을 통해 더 먼 거리를 탐사할 수 있었다. 이 기술은 특정 행성의 정렬이 필요하고 대기와의 마찰, 천체의 질량 및 공전 속도에 따라 제한이 있을 수 있지만, 우주 탐사에서 중요한 역할을 한다.

더 읽어볼만한 페이지

  • 중력의 영향 - 조산 운동
    조산 운동은 지각 변동으로 산맥이 형성되는 과정을 의미하며, 판 구조론에 기반하여 섭입, 대륙 충돌 등의 요인으로 발생하고, 윌슨 순환을 통해 해양 분지의 열림과 닫힘, 산맥 형성, 침식 과정을 거쳐 전 세계 지질 구조 형성에 영향을 미친다.
  • 중력의 영향 - 조석력
    조석력은 물체가 다른 물체의 중력에 의해 받는 힘으로, 천체의 크기와 거리에 따라 달라지며, 물체를 찌그러뜨리거나 파괴하고, 조석 고정, 조석 가열, 지진 활동 유발 등 다양한 효과를 발생시킨다.
  • 우주선 추진 - 호만 전이 궤도
    호만 전이 궤도는 우주선을 낮은 원형 궤도에서 높은 원형 궤도로 이동시키는 데 사용되는 타원 궤도로, 두 번의 엔진 점화를 통해 궤도를 변경하며, 특정 조건 하에서 최소 에너지를 사용하는 궤도 전이 방법이다.
  • 우주선 추진 - 홀 효과 추력기
    홀 효과 추력기는 정전기적 전위를 이용해 이온을 가속하여 추력을 발생시키는 전기 추진 시스템으로, 1960년대 소련에서 최초로 실용화되어 위성 궤도 유지 등에 활용되며, 화학 로켓보다 높은 비추력과 효율을 제공한다.
  • 천체동역학 - 호만 전이 궤도
    호만 전이 궤도는 우주선을 낮은 원형 궤도에서 높은 원형 궤도로 이동시키는 데 사용되는 타원 궤도로, 두 번의 엔진 점화를 통해 궤도를 변경하며, 특정 조건 하에서 최소 에너지를 사용하는 궤도 전이 방법이다.
  • 천체동역학 - 목성 얼음 위성 탐사선
    목성 얼음 위성 탐사선(Juice)은 유럽 우주국(ESA)의 목성 탐사선으로, 목성과 위성들의 대기, 표면, 내부 구조, 자기장을 탐사하며, 특히 가니메데의 해양층과 자기장 상호 작용을 상세히 조사하고, 유로파에서 생명체 관련 화학 물질과 얼음 지각 두께를 측정할 예정이다.
스윙바이
개요
이름스윙바이
다른 이름중력 도움
중력 보조
중력 가속
유형궤도 기동
목적우주선의 속도나 궤도를 변경
작동 원리
설명행성이나 다른 천체의 중력을 이용하여 우주선의 궤도와 속도를 조절하는 방법
운동량 보존스윙바이 과정에서 우주선은 천체의 운동량 일부를 교환하며, 이로 인해 우주선의 속도와 방향이 변경됨
효과
속도 변화우주선의 속도를 증가시키거나 감소시킬 수 있음
궤도 변경우주선의 궤도 경사, 주기, 이심률 등을 변경할 수 있음
연료 절약스윙바이를 통해 우주 탐사선의 연료 소모를 줄이고, 더 먼 거리를 탐사할 수 있게 함
활용
주요 임무보이저
갈릴레오
카시니
뉴 허라이즌스
심우주 탐사태양계 외부 행성 탐사, 혜성 탐사 등에 활용
궤도 수정인공위성의 궤도 유지 및 변경
장점 및 단점
장점연료 소비 감소
탐사 가능 범위 확대
임무 기간 단축
단점정확한 궤도 계산 및 제어 필요
천체의 위치 및 궤도에 대한 정확한 정보 필요
스윙바이 기회 제한
추가 정보
관련 개념델타-V
궤도 역학
중력

2. 역사

1970년대 초반까지는 우주선의 자체 추진력에만 의존해 목성 이상을 탐사할 수 없었으나, 스윙바이 덕에 보이저 호는 목성을 넘어 해왕성까지 탐사할 수 있었다. 스윙바이를 활용해 처음으로 토성에 다다른 탐사선은 1973년 발사된 파이어니어 11호다. 현재는 대부분의 탐사선이 스윙바이를 이용해 다른 행성 궤도에 진입하고 있으며, 연료를 절약하고 빠른 시간 안에 목적지에 도착할 수 있어 경제적, 시간적으로 유리하다.[6][7][8][9][10][11][12][13][14][15]

2. 1. 초기 개념

유리 콘드라튜크는 1918년~1919년 작성되어 1938년에 출판된 논문 "건설을 위해 읽을 사람들에게"("Тем, кто будет читать, чтобы строить"ru)[6]에서 두 행성 사이를 이동하는 우주선이 두 행성의 달의 중력을 이용하여 궤도의 시작과 끝에서 가속될 수 있다고 제안했다. 하지만 중력 보조에 대한 그의 원고는 이후 개발되지 않았고 1960년대까지 출판되지 않았다.[7] 프리드리히 잔더는 1925년 논문 "제트 추진에 의한 비행 문제: 행성 간 비행"("Проблема полета при помощи реактивных аппаратов: межпланетные полеты"ru)[8]에서 중력 보조 개념 뒤에 숨겨진 물리학과 태양계 행성 간 탐사에 대한 잠재력을 깊이 이해하고 있음을 보여주었다.[7]

가에타노 크로코는 여러 중력 보조를 고려한 행성 간 여행을 처음으로 계산했다.[7]

중력 보조 기동은 1959년 소련 탐사선 루나 3호가 달의 뒷면을 촬영하면서 처음 사용되었다. 이 기동은 므스티슬라프 켈디시의 지휘 하에 켈디시 응용수학 연구소에서 수행된 연구에 의존했다.[9][10][11][12]

1961년, 미하엘 미노비치는 NASA의 제트 추진 연구소(JPL)에서 일하는 UCLA 대학원생으로서, 나중에 게리 플랜드로의 행성 그랜드 투어 아이디어에 사용될 중력 보조 기술을 개발했다.[13][14]

2. 2. 실제 적용

스윙바이는 1959년 소련의 루나 3호가 달의 뒷면을 촬영할 때 처음 사용되었다.[9][10][11][12] 이는 므스티슬라프 켈디시 지휘 하의 켈디시 응용수학 연구소의 연구를 바탕으로 이루어졌다.[9][10][11][12]

1970년대 이전까지는 우주선 자체 추진력만으로는 목성 너머 탐사가 어려웠지만, 스윙바이 덕분에 보이저 호는 해왕성까지 탐사할 수 있었다. 스윙바이를 활용해 처음으로 토성에 도달한 탐사선은 1973년 발사된 파이어니어 11호다. 현재는 대부분의 탐사선이 스윙바이를 이용해 다른 행성 궤도에 진입하며, 연료를 절약하고 빠른 시간 안에 목적지에 도착할 수 있어 경제적, 시간적으로 유리하다.

스윙바이 개념은 1918년~1919년에 유리 콘드라튜크가 제안했고,[6] 1925년 프리드리히 잔더가 그 물리학적 원리와 행성 간 탐사 가능성을 제시했다.[8][7] 1961년 미하엘 미노비치는 NASA의 제트 추진 연구소(JPL)에서 중력 보조 기술을 개발했다.[13][14]

다음은 여러 탐사선들의 스윙바이 활용 사례이다.

탐사선발사 년도내용
루나 3호1959년달 뒷면 촬영에 처음으로 스윙바이 기동 시도.[17] 속도 증가는 없었지만, 궤도 변경을 통해 사진 전송 성공.[18]
파이오니어 10호1972년목성 임무 완수 후, 중력 슬링샷 효과를 이용해 태양계 탈출 속도에 도달한 최초의 우주선.[19][20]
파이오니어 11호1973년목성에서 중력 보조를 받아 토성에 도달.[21][22][23]
마리너 10호1974년금성을 지나 수성 탐사에 성공.[24]
보이저 1호1977년목성과 토성 주변에서 슬링샷 기동으로 태양 중력 탈출 에너지를 얻음.[25]
보이저 2호1977년목성, 토성, 천왕성, 해왕성에서 스윙바이 수행.[29]
갈릴레오1989년금성(1회), 지구(2회)에서 총 3번의 중력 보조를 받아 목성에 도달.[30][31]
율리시스1990년목성에서 중력 보조(1992년)를 받아 태양 극 지역 연구.[32][33]
메신저2004년지구(1회), 금성(2회), 수성(3회) 플라이바이로 속도를 늦춰 2011년 수성 궤도 진입.[34][35]
카시니1997년금성(2회), 지구(1회), 목성(1회) 중력 보조로 2004년 토성 도착.[36][37]
로제타2004년화성(1회), 지구(3회)에서 4번의 중력 보조로 2014년 67P/추류모프-게라시멘코 혜성과 랑데부.[40][41]
뉴 호라이즌스2006년2007년 목성에서 중력 보조를 받아 2015년 명왕성 도달.[42][43]
주노2011년2013년 지구 플라이바이로 중력 보조를 받아 5년 만에 목성 도착.[44]
파커 태양 탐사선2018년금성에서 여러 차례 중력 보조를 받아 태양에 근접.
솔라 오비터2020년금성(2회), 지구(1회) 중력 보조로 태양계 안쪽 궤도 변경.[49]
베피콜롬보2018년지구(1회), 금성(2회), 수성(6회) 중력 보조로 2025년 수성 도착 예정.[50]
루시2021년지구(2회) 중력 보조 예정.[51]


3. 원리

스윙바이는 어떤 천체의 중력 에너지를 운동 에너지로 전환시키는 것이다. 스윙바이 공식은 탄성 충돌 공식에서 파생되었으며, 운동량과 운동 에너지는 충돌 전후에 보존된다(운동량 보존 법칙).

중앙이 행성, 옅은 청색이 중력장, 검은색이 우주선이며 점선은 행성에 대한 궤도, 실선은 행성에 대한 속도를 나타낸다. 진입 시와 이탈 시 속도는 변하지 않는다.


녹색은 행성의 공전 속도, 빨간색은 우주선의 행성에 대한 속도와 천체의 공전 속도의 합성 속도를 나타낸다. 공전하는 천체의 뒤쪽에서 진입하면 이탈 시에는 증속한다.


공전하는 천체의 앞쪽에서 진입하면 이탈 시에는 감속한다.


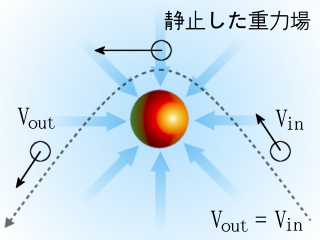
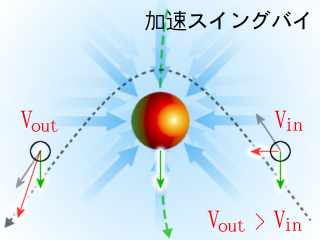
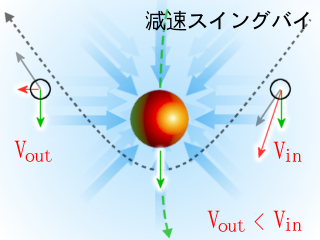
태양계 행성에서 우주선이 스윙바이를 하는 경우, 행성과 우주선만 고려하면 다음과 같다.

우주선은 행성에 접근하며 중력에 의해 가속되고, 행성 근방에서 최대 속도에 도달하며 궤도가 "く"자 모양으로 꺾인다. 이후 행성에서 멀어지며 중력으로 감속된다. 행성이 운동하지 않으면 증속과 감속은 상쇄되어 속도는 변하지 않고 운동 방향만 바뀐다.

하지만 행성은 태양 주위를 공전하므로, 행성과 우주선을 이체계로 취급하여 질량 중심 운동과 상대 운동으로 나누어 생각해야 한다. 태양계에 대한 정지계에서 우주선 운동은 행성 중력으로 궤도와 속도가 모두 변한다.

우주선이 행성 공전 방향 뒤쪽을 지나면, 행성 근처를 지난 후 멀어질 때 행성 공전 방향과 같아진다. 이때 속도는 행성 접근 시 속도에 공전 속도가 더해진다. 행성에 대한 우주선 속도는 스윙바이 전후로 변하지 않지만, 궤도가 바뀌어 태양에 대한 속도는 빨라진다. 행성에서 멀리 떨어진 경우, 우주선이 멀어지는 방향이 행성 공전 방향과 항상 같지는 않지만, 증속된다는 점은 변함없다.

반대로, 행성 공전 방향 앞쪽을 통과하면, 우주선은 행성 공전 반대 방향으로 꺾여 공전 속도만큼 감속된다.

스윙바이로 우주선이 가속되면 행성 공전 속도는 감소한다. 속도 감소로 행성은 태양에 더 가까워져 궤도 반지름이 작아지고, 다시 속도가 증가하여 안정된다. 가속 스윙바이에서는 행성 위치 에너지가 감소하고, 우주선과 행성의 운동 에너지가 증가한다. 반대로 우주선이 감속하면 행성은 태양에서 멀어지고 공전 속도가 느려지며, 우주선과 행성 운동 에너지 감소분만큼 행성 위치 에너지가 증가한다.

하지만 행성과 우주선 질량 차이가 커서 행성에 미치는 영향은 무시할 만하다. 목성과 보이저 1, 2호의 질량비는 약 2.6×1024(2.6조×1조) 대 1로, 지구와 노트북(약 2.3kg)을 비교하는 것과 같다. 보이저가 스윙바이로 15km/s에서 30km/s로 가속되면, 목성 공전 반지름은 약 1.4×10-12 m 작아지고, 공전 속도는 약 1.2×10-20 m/s 빨라진다.

질량 ''m''1 주성을 공전 반경 ''r''2in, 공전 속도 ''v''2in 원형 궤도로 공전하는 질량 ''m''2 행성에, 질량 ''m''3 우주선이 속도 ''v''3in으로 진입하여 스윙바이를 하고, 이후 행성 공전 반경 ''r''2out, 공전 속도 ''v''2out, 우주선 속도 ''v''3out이 된다고 가정한다. (단, ${\displaystyle m_{1}>m_{2}\gg m_{3}}$, 속도는 주성 기준)

행성 궤도 변화가 작으므로, 스윙바이 후 공전 궤도도 원형으로 간주한다. (정확히는 증속 스윙바이 후에는 스윙바이 지점이 원지점인 타원 궤도, 감속 스윙바이 후에는 근지점인 타원 궤도가 된다.)

주성 만유인력과 행성 공전에 의한 원심력 균형으로, ${\displaystyle {\frac {Gm_{1}m_{2}}{r_{\rm {2in}}^{2}}}={\frac {m_{2}v_{\rm {2in}}^{2}}{r_{\rm {2in}}}}}$(''G''는 만유인력 상수)이다.

스윙바이 전후 행성 운동 에너지, 행성의 주성에 대한 위치 에너지, 우주선 운동 에너지 합은 같으므로, ${\displaystyle {\frac {1}{2}}m_{2}v_{\rm {2in}}^{2}-{\frac {Gm_{1}m_{2}}{r_{\rm {2in}}}}+{\frac {1}{2}}m_{3}v_{\rm {3in}}^{2}={\frac {1}{2}}m_{2}v_{\rm {2out}}^{2}-{\frac {Gm_{1}m_{2}}{r_{\rm {2out}}}}+{\frac {1}{2}}m_{3}v_{\rm {3out}}^{2}}$ (단, ''r''2in이 매우 작지 않으면 우주선의 주성에 대한 위치 에너지 변화는 무시)이다.

계산하면, 행성 공전 반경과 속도 변화는 우주선이 얻은 에너지 ${\displaystyle E\left(=\frac{1}{2}m_{3}v_{\rm {3out}}^{2}-\frac{1}{2}m_{3}v_{\rm {3in}}^{2}\right)}$로 ${\displaystyle \Delta r_{2}=r_{\rm {2out}}-r_{\rm {2in}}\simeq -2{\frac {r_{\rm {2in}}^{2}E}{Gm_{1}m_{2}}}}$, ${\displaystyle \Delta v_{2}=v_{\rm {2out}}-v_{\rm {2in}}\simeq {\frac {E}{m_{2}v_{\rm {2in}}}}}$와 같이 나타낼 수 있다. 즉, 스윙바이로 우주선 운동 에너지가 증가하면 행성 공전 반경은 작아지고 공전 속도는 빨라지지만, 매우 미세하여 무시할 수 있다.

3. 1. 가속 및 감속

스윙바이는 행성을 이용하여 방향을 바꿀 수 있을 뿐만 아니라, 필요에 따라 가속하거나 감속할 수 있다. 스윙바이 공식은 탄성 충돌 공식에서 파생되었다. 운동량 보존 법칙에 따라 운동량과 운동 에너지는 충돌 전후에 보존된다.

질량을 ${\displaystyle m_{1}}$, ${\displaystyle m_{2}}$, 충돌 전 속도를 ${\displaystyle u_{1}}$, ${\displaystyle u_{2}}$, 충돌 후 속도를 ${\displaystyle v_{1}}$, ${\displaystyle v_{2}}$라고 하면, 충돌 전후의 운동량은 아래와 같이 표현된다.

${\displaystyle m_{1}u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}}$

운동 에너지는 아래와 같이 표현된다.

${\displaystyle {\frac {1}{2}}m_{1}u_{1}^{2}+{\frac {1}{2}}m_{2}u_{2}^{2}={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}}$

${\displaystyle u_{1}}$와 ${\displaystyle u_{2}}$를 알 때, 위 두 등식을 연립하여 ${\displaystyle v_{1}}$와 ${\displaystyle v_{2}}$를 구할 수 있다.

${\displaystyle v_{1}={\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}u_{1}+{\frac {2m_{2}}{m_{1}+m_{2}}}u_{2}}$

${\displaystyle v_{2}={\frac {2m_{1}}{m_{1}+m_{2}}}u_{1}+{\frac {m_{2}-m_{1}}{m_{1}+m_{2}}}u_{2}}$

우주선이 행성을 스쳐 지나갈 때, 우주선의 질량(${\displaystyle m_{1}}$)은 행성의 질량(${\displaystyle m_{2}}$)에 비해 무시할 수 있을 정도로 작다. (${\displaystyle m_{1}\ll m_{2}}$)

그러므로

${\displaystyle v_{1}\approx -u_{1}+2u_{2}}$

${\displaystyle v_{2}\approx u_{2}}$

정지해 있는 행성에 탐사선이 접근하면, 탐사선은 행성의 중력에 의해 점점 빨라진다. 행성과 가장 가까운 지점에서 속도가 최대가 되고, 이후 행성에서 멀어지면서 중력 때문에 감속되어 결국 원래 속도로 돌아온다. 그러나 실제 행성은 궤도 운동을 하므로, 탐사선과 행성이 접근하는 시간은 길고 멀어지는 시간은 짧도록 궤도를 만들 수 있다. 즉, 가속되는 시간은 길고 감속되는 시간은 짧아져, 연료 없이도 더 빠른 속도를 얻을 수 있다. 행성의 인력권을 벗어나면 우주 공간은 진공이라 마찰이 거의 없어, 스윙바이로 얻은 속력을 유지한다.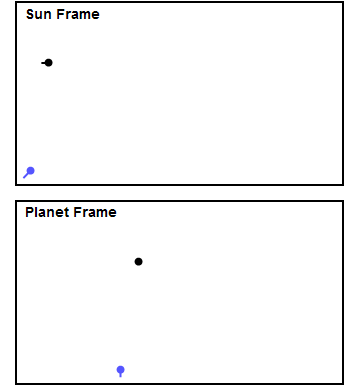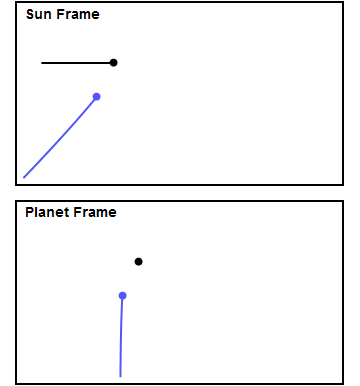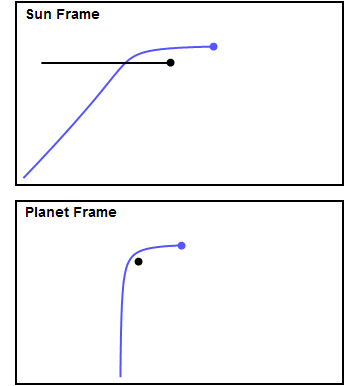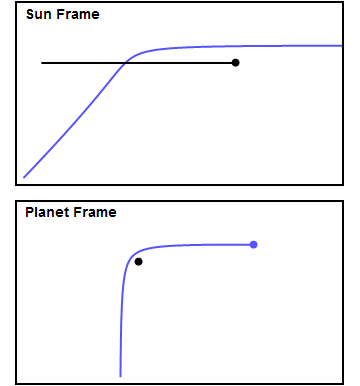



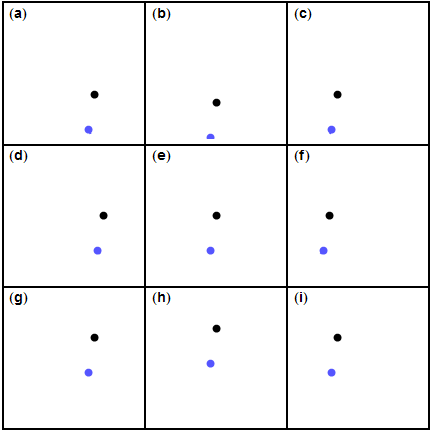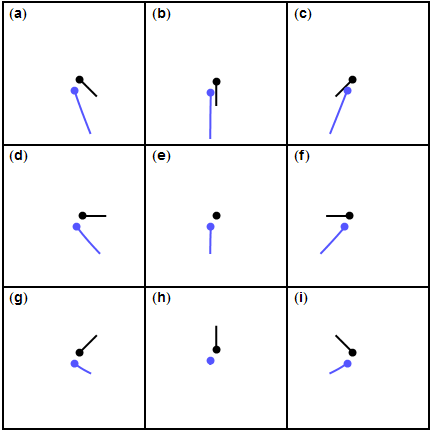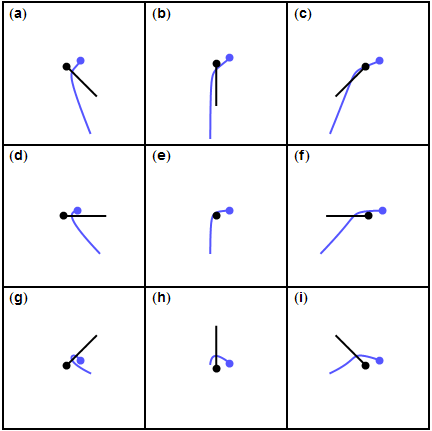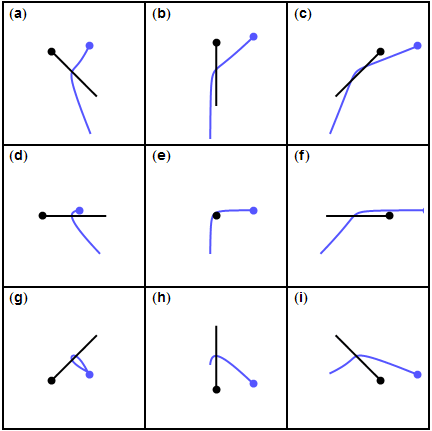
들어오는 우주선의 속도 벡터와 비행 위치에 따라 가능한 중력 보조 기동의 결과


행성 주위의 중력 보조는 행성의 중력 영향권에 진입하고 나가면서 우주선의 속도(태양에 상대적)를 변경한다. 탄성 충돌처럼 두 물체의 운동 에너지 합은 일정하게 유지된다. 슬링샷 기동으로 우주선의 궤적과 태양에 대한 속도를 바꿀 수 있다.[3]

움직이는 기차 앞에서 테니스공이 튕기는 것을 생각해 보자. 기차 플랫폼에서 시속 30km/h로 공을 던지고, 시속 50km/h로 접근하는 기차를 향해 던진다고 가정하자. 기차 운전사는 공이 시속 80km/h로 접근하고, 탄성 충돌 후 시속 80km/h로 떠나는 것을 본다. 그러나 기차의 움직임 때문에 기차 플랫폼에서는 공이 시속 130km/h로 보인다. 공은 자체 속도에 기차 속도의 두 배를 더한 것이다.[4]

이를 우주로 확장하면, 행성 좌표계에서 우주선은 행성에 상대적으로 수직 속도 ''v''를 갖는다. 슬링샷 후 우주선은 90도 각도로 떠나며, 여전히 ''v''의 속도를 갖지만 수평 방향이다.[2] 태양 기준 프레임에서 행성은 v의 수평 속도를 갖고, 피타고라스 정리를 이용하면 우주선은 처음에 ${\displaystyle {\sqrt {2}}}$''v''의 속도를 갖는다. 우주선이 행성을 떠난 후 ''v + v ='' 2''v''의 속도를 가져, 약 0.6''v''를 얻는다.[2]

이 예는 단순하지만, 쌍곡선 경로로 이동하면 엔진 작동 없이 반대 방향으로 행성을 떠날 수 있다. 이는 우주선이 경험할 수 있는 여러 궤적과 속도 증가 중 하나일 뿐이다.

에너지 및 운동량 보존 법칙에 위배되는 것처럼 보일 수 있지만, 우주선이 행성에 미치는 영향도 고려해야 한다. 우주선이 얻는 선형 운동량은 행성이 잃는 것과 크기가 같아, 우주선은 속도를 얻고 행성은 속도를 잃는다. 그러나 행성의 엄청난 질량 때문에 속도 변화는 무시할 정도이다. 예를 들어 1 미터톤은 행성 간 우주 탐사선의 일반적인 질량이고, 목성은 약 2 x 1024 미터톤의 질량의 크기를 갖는다. 목성을 통과하는 1톤 우주선은 이론적으로 행성이 km/s당 약 5 x 10−25 km/s의 궤도 속도를 잃게 한다. 따라서 행성에 미치는 영향은 무시할 수 있다.[5]

우주에서의 만남을 현실적으로 묘사하려면 3차원을 고려해야 한다. 위와 같은 원리가 적용되지만, 행성 속도를 우주선 속도에 더하려면 벡터 덧셈이 필요하다.

중력 슬링샷의 2차원 개략도. 화살표는 우주선이 만남 전후 이동하는 방향을, 화살표 길이는 속도를 나타낸다.


지구를 중력 슬링샷으로 사용하여 수성을 공전하는 궤도에 진입하기 위해 감속하는 MESSENGER의 모습


궤도의 가역성 때문에 중력 슬링샷은 우주선 속도를 줄이는 데에도 사용된다. 마리너 10호와 MESSENGER는 수성에 도달하기 위해 이 기동을 수행했다.

근점 근처에서 로켓 연소를 하면 연료를 가장 적게 사용한다. 로켓 연소는 항상 같은 속도 변화(Δv)를 주지만, 운동 에너지 변화는 연소 시 차량 속도에 비례한다. 따라서 최대 운동 에너지는 차량의 최대 속도(근점)에서 연소할 때 얻는다. 오베르트 효과는 이 기술을 자세히 설명한다.

태양계 행성에서 우주선이 스윙바이를 하는 경우를 상정하여 행성과 우주선만으로 구성된 모델을 통해 스윙바이 과정을 간략하게 설명하면 다음과 같다. 우주선이 행성에 접근하면 중력에 끌려 서서히 가속된다. 행성 근방에서 속도가 최대가 되고, 궤도는 "く"자 모양으로 꺾인다. 이후 행성에서 멀어질 때 중력으로 감속된다. 행성이 운동하지 않으면 증속과 감속은 상쇄되어 속도는 변하지 않는다.

하지만 행성은 태양 주위를 공전하므로, 행성과 우주선을 이체계로 취급하여 질량 중심 운동과 상대 운동으로 생각해야 한다. 태양계에 대한 정지계에서 우주선 운동은 행성 중력으로 궤도와 속도가 변한다.

우주선이 행성 공전 방향 뒤쪽을 지나면, 행성 근처를 지난 후 우주선이 행성에서 멀어질 때의 방향은 행성 공전과 같아진다. 이때 속도는 행성 접근 시 속도에 공전 속도가 더해진다. 즉, 행성에 대한 우주선 속도는 스윙바이 전후로 변하지 않지만, 궤도가 바뀌어 태양에 대한 속도는 빨라진다.

엄밀히 말하면, 우주선 궤도가 행성에서 멀리 떨어져 있는 경우 등에는 우주선이 행성에서 멀어질 때의 방향이 행성의 공전과 같은 방향이 되지 않을 수도 있다. 그 경우에도 증속되는 양은 적어지지만, 증속된다는 점에는 변함이 없다.

반대로, 행성 공전 방향 앞쪽을 통과하면, 우주선은 행성 공전과 반대 방향으로 방향을 바꾸어 공전 속도만큼 속도가 감소한다.

3. 2. 에너지 교환

스윙바이는 어떤 천체의 중력 에너지를 운동 에너지로 전환시키는 것이다. 스윙바이 공식은 탄성 충돌 공식에서 파생되었다.

운동량과 운동 에너지는 충돌 전후에 보존된다(운동량 보존 법칙). 질량을 m_1, m_2라고 하고, 충돌 전 속도를 u_1, u_2, 충돌 후 속도를 v_1, v_2라고 하면, 충돌 전후의 운동량은 아래와 같이 표현된다.

m_1

u_1

+

m_2

u_2

=

m_1

v_1

+

m_2

v_2



운동 에너지는 아래와 같이 표현된다.

\frac{1}{2}

m_1

u_1^2

+

\frac{1}{2}

m_2

u_2^2

=

\frac{1}{2}

m_1

v_1^2

+

\frac{1}{2}

m_2

v_2^2

u_1와 u_2를 알 때, 위 두 등식을 연립하여 v_1와 v_2를 구할 수 있다.

v_1

=

\frac{m_1-m_2}{m_1+m_2}

u_1

+

\frac{2m_2}{m_1+m_2}

u_2

v_2

=

\frac{2m_1}{m_1+m_2}

u_1

+

\frac{m_2-m_1}{m_1+m_2}

u_2

우주선이 행성을 스쳐 지나갈 때, 우주선의 질량(m_1)은 행성의 질량(m_2)에 비해 매우 작으므로(m_1

\ll

m_2), 다음이 성립한다.

v_1

\approx

  • u_1

+

2u_2



v_2

\approx

u_2

정지해 있는 행성에 탐사선이 접근하면, 탐사선은 행성의 중력에 의해 점점 빨라진다. 행성과 가장 가까운 지점에서 속도가 최대가 되고, 이후 멀어지면서 감속되어 결국 원래 속도가 된다. 그러나 행성은 실제로 궤도운동을 하므로, 탐사선과 행성이 접근하는 시간은 길고 멀어지는 시간은 짧게 궤도를 형성하면, 연료 없이도 더 빠른 속도를 얻을 수 있다. 행성의 인력권을 벗어나면, 우주 공간은 진공이라 마찰이 작용하지 않아 얻은 속력을 유지할 수 있다.

행성 주위의 중력 보조는 행성의 중력 영향권에 진입하고 나가면서 우주선의 속도(태양에 상대적)를 변경한다. 두 물체의 운동 에너지의 합은 일정하게 유지된다(탄성 충돌 참조). 따라서 슬링샷 기동을 사용하여 우주선의 궤적과 태양에 대한 속도를 변경할 수 있다.[3]

움직이는 기차 앞에서 테니스공이 튕기는 것을 생각해 보자. 기차 플랫폼에 서서 시속 30km/h로, 시속 50km/h로 접근하는 기차를 향해 공을 던진다고 가정하면, 기차 운전사는 공이 시속 80km/h로 접근하고, 튕겨 나간 후 시속 80km/h로 떠나는 것을 본다. 그러나 기차의 움직임 때문에, 기차 플랫폼 기준으로는 시속 130km/h이다. 공은 자체 속도에 기차 속도의 두 배를 더한 것이다.[4]

이 유추를 우주로 변환하면, 행성의 좌표계에서 우주선은 행성에 상대적으로 수직 속도 ''v''를 갖는다. 슬링샷 후 우주선은 90도 각도로 떠나고, 여전히 ''v''의 속도를 갖지만 수평 방향이다.[2] 태양 기준 프레임에서 행성은 v의 수평 속도를 가지며, 피타고라스 정리를 사용하면 우주선은 처음에 ''v''의 속도를 갖는다. 우주선이 행성을 떠난 후에는 ''v + v ='' 2''v''의 속도를 갖게 되어 약 0.6''v''를 얻는다.[2]

이 예는 단순화된 것이지만, 우주선이 쌍곡선 경로로 이동하면 엔진 작동 없이 반대 방향으로 행성을 떠날 수 있다.

에너지 보존 및 운동량 보존 법칙에 위배되는 것처럼 보일 수 있지만, 우주선이 행성에 미치는 영향도 고려해야 한다. 우주선이 얻는 선형 운동량은 행성이 잃는 것과 크기가 같으므로, 우주선은 속도를 얻고 행성은 속도를 잃는다. 그러나 행성의 질량이 매우 커서, 행성의 속도 변화는 다른 천체와의 상호 작용으로 인한 궤도 섭동과 비교해도 무시할 정도로 작다. 예를 들어, 1 미터톤은 행성 간 우주 탐사선의 전형적인 질량인 반면, 목성은 약 2 x 1024 미터톤의 질량의 크기를 가진다. 따라서 목성을 통과하는 1톤의 우주선은 이론적으로 행성이 우주선이 얻는 km/s당 약 5 x 10−25 km/s의 궤도 속도를 잃게 한다. 따라서 행성에 미치는 영향은 무시할 수 있다.[5]

우주에서의 만남에 대한 현실적인 묘사는 3차원을 고려해야 한다. 위와 동일한 원리가 적용되지만, 행성의 속도를 우주선의 속도에 추가하려면 아래와 같이 벡터 덧셈이 필요하다.

궤도의 가역성 때문에 중력 슬링샷은 우주선의 속도를 줄이는 데에도 사용될 수 있다. 마리너 10호와 MESSENGER는 수성에 도달하기 위해 이 기동을 수행했다.

중력 보조만으로는 필요한 속도보다 더 많은 속도가 필요한 경우, 근점(가장 가까운 행성 접근) 근처에서 로켓 연소를 수행하면 연료를 가장 적게 사용한다. 주어진 로켓 연소는 항상 동일한 속도 변화(Δv)를 제공하지만, 운동 에너지의 변화는 연소 시 차량의 속도에 비례한다. 따라서 최대 운동 에너지는 연소가 차량의 최대 속도(근점)에서 발생할 때 얻는다. 오베르트 효과는 이 기술을 더 자세히 설명한다.

태양계의 행성에서 우주선이 스윙바이를 하는 경우를 생각해 보자. 우선 행성과 우주선만으로 생각해 보자.

우주선이 목표 행성에 접근하면, 행성의 중력에 의해 끌어당겨져 서서히 가속된다. 행성 근방을 지나갈 때 속도가 최대가 되며, 궤도는 "く"자 모양으로 꺾인다. 그 후, 행성에서 멀어질 때는 중력이 끌어당기는 힘으로 작용하여 감속한다.

행성이 운동하지 않는다면, 우주선이 행성의 중력권에 진입할 때의 증속과 이탈할 때의 감속은 상쇄된다. 즉, 스윙바이에 의해 운동 방향은 바뀌지만, 속도는 변하지 않는다.

하지만 실제로는 행성은 태양 주위를 공전하고 있기 때문에, 그 운동의 영향을 고려해야 한다. 즉, 행성과 우주선을 이체계로 취급하여, 질량 중심 운동과 상대 운동으로 나누어 생각해야 한다. 이때, 태양계에 대한 정지계로 표현한 우주선의 운동은, 행성의 중력의 영향을 받아, 궤도가 바뀔 뿐만 아니라, 그 속도도 변화하게 된다.

우주선이 행성의 공전 방향 뒤쪽을 지나면, 행성 근처를 지난 후 우주선이 행성에서 멀어질 때의 방향은 행성의 공전과 같은 방향이 된다. 이때의 속도는 행성에 접근할 때의 속도에 공전 속도만큼 더해진 속도가 된다. 즉, 행성에 대한 우주선의 속도는 스윙바이 전후로 변하지 않지만, 궤도가 바뀌었기 때문에 태양에 대한 우주선의 속도는 빨라진다.

엄밀히 말하면, 우주선의 궤도가 행성에서 멀리 떨어져 있는 경우 등에는 우주선이 행성에서 멀어질 때의 방향이 행성의 공전과 같은 방향이 되지 않을 수도 있다. 그 경우에도 증속되는 양은 적어지지만, 증속된다.

반대로, 행성의 공전 방향의 앞쪽을 통과하면, 우주선은 행성의 공전과 반대 방향으로 방향을 바꾸어, 공전 속도만큼 속도가 감소한다.

스윙바이를 통해 우주선이 가속되면, 그만큼 행성의 공전 속도가 감소하게 된다. 속도가 떨어짐으로써 행성은 태양에 약간 더 가까워지고, 궤도 반지름이 작아지기 때문에 다시 속도는 증가하여 안정된다. 결국, 가속 스윙바이에서는 행성의 위치 에너지가 감소하고, 우주선의 운동 에너지와 행성의 운동 에너지가 그만큼 증가한다.

반대로, 스윙바이에 의해 우주선이 감속하는 경우, 행성은 약간 태양에서 멀어지고, 공전 속도가 늦어진다. 그리고, 우주선의 운동 에너지와 행성의 운동 에너지가 감소한 만큼, 행성의 위치 에너지가 증가한다.

하지만, 행성과 우주선의 질량비는 매우 크기 때문에, 행성에 대한 영향은 무시할 수 있을 정도로 작다. 예를 들어, 목성과 보이저 1호나 2호의 질량비는 2.6×1024(2.6조×1조) 대 1 정도이며, 지구와 약간 무거운 노트북(2.3kg 정도)을 비교하는 것과 같다. 스윙바이에 의해 보이저가 15km/s에서 30km/s로 가속되었다고 하면, 그로 인해, 목성의 공전 반지름은 약 1.4×10-12 m 작아지고, 공전 속도는 약 1.2×10-20 m/s 빨라지게 된다.

질량 ''m''1의 주성을 공전 반경 ''r''2in의 원형 궤도로 공전 속도 ''v''2in으로 공전하는 질량 ''m''2의 행성에 대해, 질량 ''m''3의 우주선이 속도 ''v''3in으로 진입하여 스윙 바이를 수행한다고 가정한다. 그리고 스윙 바이 후의 행성의 공전 반경은 ''r''2out, 공전 속도는 ''v''2out, 우주선의 속도는 ''v''3out이 된다고 가정한다. 단, m_1 > m_2 \gg m_3이며, 속도는 주성에 대한 것이다.

행성의 궤도 변화는 작으므로, 스윙 바이 후의 공전 궤도도 원형으로 간주하여 개략적으로 계산한다. 스윙 바이 후의 행성 궤도에 대해 정확히 말하면, 증속 스윙 바이 수행 후에는 스윙 바이가 수행된 부근을 원지점으로 하는 타원 궤도가 되며, 감속 스윙 바이 수행 후에는 스윙 바이가 수행된 부근을 근지점으로 하는 타원 궤도가 된다.

주성의 만유인력과 행성의 공전에 의한 원심력이 균형을 이루고 있으므로, 다음과 같은 관계가 있다. ''G''는 만유인력 상수이다.

:\frac{G m_1 m_2}{r_{\rm 2in}^2}=\frac{m_2 v_{\rm 2in}^2}{r_{\rm 2in}}

스윙 바이 전후로, 행성의 운동 에너지와 행성의 주성에 대한 위치 에너지와 우주선의 운동 에너지의 합계는 같으므로, 다음과 같은 관계가 있다. 단, 매우 ''r''2in이 작은 경우 외에는 우주선의 주성에 대한 위치 에너지의 변화는 무시할 수 있다.

:\frac{1}{2}m_2 v_{\rm 2in}^2 - \frac{G m_1 m_2}{r_{\rm 2in}} + \frac{1}{2} m_3 v_{\rm 3in}^2=\frac{1}{2} m_2 v_{\rm 2out}^2 - \frac{G m_1 m_2}{r_{\rm 2out}} + \frac{1}{2} m_3 v_{\rm 3out}^2

이들을 계산하면, 행성의 공전 반경과 공전 속도의 변화는 우주선이 얻은 에너지 E \left(=\frac{1}{2} m_3 v_{\rm 3out}^2 - \frac{1}{2} m_3 v_{\rm 3in}^2 \right)를 사용하여 다음과 같이 나타낼 수 있다.

:\Delta r_2=r_{\rm 2out} - r_{\rm 2in} \simeq -2 \frac{r_{\rm 2in}^2 E}{G m_1 m_2}

:\Delta v_2=v_{\rm 2out} - v_{\rm 2in} \simeq \frac{E}{m_2 v_{\rm 2in}}

즉, 스윙 바이로 우주선의 운동 에너지가 증가(가속)하는 경우, 행성의 공전 반경은 작아지고, 행성의 공전 속도는 빨라진다. 그렇다고 해도, 매우 미세한 변화이며, 거의 무시할 수 있는 양이다.

4. 파워드 스윙바이

스윙바이 시에 우주선의 추력을 함께 사용하는 것을 '''파워드 스윙바이'''라고 한다.

행성 중심에서 생각하면 에너지 보존 법칙에 의해 근지점에서의 속도 ''v'', 지심 거리 ''R'', 무한대에서의 속도 v_\infty는 다음과 같다.

:E={1 \over 2}mv^2 - {GMm \over R}={1 \over 2}mv_\infty^2

여기서 근지점에서 ''v''를 v + \delta v로 속도를 높였을 때 무한대에서의 속도 변화 \delta v_\infty를 생각하면

: \delta v_\infty={\sqrt{v_\infty^2 + {2GM \over R}} \over v_\infty} \delta v

가 되며, 근지점에서의 가속은 무한대에서의 가속보다 효과가 크다는 것을 알 수 있다. 예를 들어 v_\infty=3 \, {\rm km/s}, 근지점 고도 200 km (''R''=6578 km)에서 지구를 스윙바이하는 것을 생각하면, \delta v_\infty=3.7 \delta v가 된다.

5. 장점 및 한계

스윙바이는 우주선의 연료를 절약하고 효율적으로 탐사하기 위한 중요한 기술이지만, 몇 가지 한계점도 가지고 있다.


  • 행성 배열의 제약: 스윙바이를 효과적으로 활용하려면 행성들이 특정 위치에 있어야 한다. 보이저 탐사선이 목성, 토성, 천왕성, 해왕성을 모두 방문할 수 있었던 것은 1970년대 후반의 "대 순회" 정렬 덕분이었다. 이러한 기회는 매우 드물게 찾아온다.
  • 대기 항력: 행성에 너무 가까이 접근하면 대기 항력으로 인해 오히려 속도가 줄어들 수 있다. 따라서 대기가 있는 행성을 이용할 때는 적절한 고도를 유지하는 것이 중요하다.
  • 정밀한 궤도 조정: 스윙바이를 성공적으로 수행하려면 매우 정밀한 궤도 조정이 필요하다. 예를 들어, JAXA의 하야부사 탐사선은 지구 근처 1km 범위 내를 속도 오차 1cm/s 이내로 통과해야 했다.
  • 천체 질량과 공전 속도: 천체의 질량과 공전 속도가 클수록 궤도와 속도의 변화를 크게 할 수 있다. 질량이 작은 천체에서는 공전 속도가 빨라도 궤도를 바꿀 수 없고 통과할 뿐이다. 반대로 질량이 크더라도 공전 속도가 작은 천체에서는 궤도는 바꿀 수 있지만 속도에 미치는 영향은 작아진다.


이러한 한계점에도 불구하고, 스윙바이는 여전히 우주 탐사에서 매우 유용한 기술이며, 앞으로도 널리 활용될 것으로 예상된다.

5. 1. 장점

스윙바이는 행성을 이용해 방향을 바꿀 수 있을 뿐만 아니라 필요에 따라 가속하거나 감속할 수 있다. 행성 주위의 중력 보조는 행성의 중력 영향권에 진입하고 나가면서 우주선의 속도 (태양에 상대적)를 변경한다. 이때 두 물체의 운동 에너지의 합은 일정하게 유지된다. (탄성 충돌 참조) 따라서 슬링샷 기동을 사용하여 우주선의 궤적과 태양에 대한 속도를 변경할 수 있다.[3]

지상에서의 유사한 예로 움직이는 기차 앞에서 테니스공이 튕기는 상황을 생각할 수 있다. 기차 플랫폼에 서서 시속 30km/h로 공을 던지고, 시속 50km/h로 접근하는 기차를 향해 던진다고 가정해 보자. 기차 운전사는 공이 시속 80km/h로 접근하는 것을 보고, 공이 기차 앞면에서 탄성적으로 튕겨 나간 후 시속 80km/h로 떠나는 것을 본다. 그러나 기차의 움직임 때문에, 기차 플랫폼에서 보면 공은 시속 130km/h로 움직이게 된다. 즉, 공은 자체 속도에 기차 속도의 두 배를 더한 속도를 얻게 된다.[4]

이 유추를 우주로 가져오면, 행성의 좌표계에서 우주선은 행성에 상대적으로 수직 속도 ''v''를 갖는다. 슬링샷 후 우주선은 도착한 것과 90도 각도로 코스를 떠나며, 여전히 ''v''의 속도를 갖지만 수평 방향이다.[2] 태양 기준 프레임에서 행성은 v의 수평 속도를 가지며, 피타고라스 정리를 사용하여 우주선은 처음에 총 속도 ''v''를 갖는다. 우주선이 행성을 떠난 후에는 ''v + v ='' 2''v''의 속도를 갖게 되어 약 0.6''v''를 얻는다.[2]

이 설명은 에너지 보존 및 운동량 보존 법칙에 위배되는 것처럼 보일 수 있지만, 우주선이 행성에 미치는 영향도 고려해야 한다. 우주선이 얻는 선형 운동량은 행성이 잃는 것과 크기가 같으므로, 우주선은 속도를 얻고 행성은 속도를 잃는다. 그러나 행성의 질량이 매우 크기 때문에, 행성의 속도 변화는 무시할 정도로 작다. 예를 들어, 목성은 1톤의 우주선보다 훨씬 큰 2 x 1024 미터톤의 질량을 가지고 있다. 따라서 목성을 통과하는 1톤의 우주선은 이론적으로 행성이 우주선이 얻는 km/s당 약 5 x 10−25 km/s의 궤도 속도를 잃게 한다. 모든 실용적인 목적을 위해 행성에 미치는 영향은 무시할 수 있다.[5]

궤도의 가역성 때문에 중력 슬링샷은 우주선의 속도를 줄이는 데에도 사용할 수 있다. 마리너 10호와 MESSENGER는 수성에 도달하기 위해 이 기동을 수행했다.



중력 보조만으로는 충분한 속도를 얻을 수 없는 경우, 근점 (가장 가까운 행성 접근) 근처에서 로켓 연소를 수행하면 연료를 가장 적게 사용하면서 속도를 크게 변화시킬 수 있다. 주어진 로켓 연소는 항상 동일한 속도 변화 (Δv)를 제공하지만, 운동 에너지의 변화는 연소 시 차량의 속도에 비례하기 때문이다. 따라서 최대 운동 에너지는 연소가 차량의 최대 속도(근점)에서 발생할 때 얻는다. 오베르트 효과는 이 기술을 더 자세히 설명한다.

지구에서 내부 행성으로 이동하는 우주선은 태양을 향해 낙하하기 때문에 상대 속도가 증가하고, 지구에서 외부 행성으로 이동하는 우주선은 태양의 근접 지역을 벗어나기 때문에 속도가 감소한다. 내부 행성의 공전 속도는 지구보다 빠르지만, 내부 행성으로 이동하는 우주선은 태양의 중력에 의해 목적지 행성의 공전 속도보다 훨씬 빠른 속도로 가속된다. 따라서 우주선이 해당 내부 행성의 궤도에 진입하려면 속도를 늦출 방법이 필요하다. 마찬가지로 외부 행성의 공전 속도는 지구보다 느리지만, 외부 행성으로 이동하는 우주선은 태양의 중력에 의해 해당 외부 행성의 공전 속도보다 훨씬 느린 속도로 감소한다. 따라서 외부 행성의 궤도에 진입하려면 해당 행성에 도달했을 때 우주선을 가속할 방법이 있어야 한다.

로켓 엔진은 우주선의 속도를 높이고 낮추는 데 사용할 수 있지만, 로켓 추진은 추진제를 사용하고, 추진제에는 질량이 있다. 속도 변화가 작더라도 (Δ''v''로 알려짐) 지구의 중력 우물에서 벗어나는 데 필요한 추진제가 훨씬 더 많이 필요하다. 이륙 질량 요구 사항은 우주선의 필요한 델타-''v''의 증가에 따라 지수적으로 증가한다.

연료를 우주로 들어 올리려면 추가 연료가 필요하기 때문에, 우주 임무는 "델타-v 예산"으로 알려진 타이트한 추진제 "예산"으로 설계된다. 델타-v 예산은 지구를 떠난 후 속도 증가, 속도 감소, 외부의 충격에 대한 안정화 또는 방향 변경을 위해 사용할 수 있는 총 추진제이다. 전체 임무는 해당 능력 내에서 계획되어야 한다. 따라서 연료를 연소할 필요가 없는 속도 및 방향 변경 방법은 유리하다. 중력 보조 기동은 추진제를 소모하지 않고도 우주선의 속도를 크게 변경할 수 있으며 상당한 양의 추진제를 절약할 수 있으므로, 연료 절약을 위한 매우 일반적인 기술이다.

천체의 질량과 공전 속도가 클수록 궤도와 속도의 변화를 크게 할 수 있다. 질량이 작은 천체에서는 공전 속도가 빨라도 궤도를 바꿀 수 없고 통과할 뿐이다. 반대로 질량이 크더라도 공전 속도가 작은 천체에서는 궤도는 바꿀 수 있지만 속도에 미치는 영향은 작아진다.

천체에 가까워질수록 궤도는 크게 굽어지고, 반대로 천체에서 멀리 통과할수록 궤도는 변하지 않는다. 따라서 스윙바이를 사용하여 예정된 궤도로 변경하기 위해서는 천체의 중력권에 들어가기 전 궤도 조정에 상당한 정밀함이 요구된다. 예를 들어, JAXA의 공학 실험 탐사선 하야부사는 지구 근처의 1km 범위 내를 속도 오차 1cm/s 이내로 통과하도록 스윙바이를 수행하기 위해 29일 전과 7일 전에 궤도가 미세 조정되었다. 궤도를 조정할 때는 연료를 사용하여 제어를 하는데, 이때에도 연료 소비를 최대한 최소화하고, 지구와 교신하기 위한 안테나의 방향을 바꾸지 않는 등 다른 조건도 지킬 수 있도록 주의를 기울인다.

5. 2. 한계

스윙바이는 탐사선이 행성에 너무 가까이 접근하면 행성의 중력에 이끌려 충돌할 위험이 있다. 그러나, 현대 기술의 발달로 정밀한 계산을 통해 이러한 위험을 극복하고, 행성에 빨려 들어갈 위기에서도 벗어날 수 있다.[2]

행성 주위에서 중력 보조를 받으면 행성의 중력 영향권을 통과하면서 탐사선의 속도 (태양 기준)가 변한다. 이때 두 물체의 운동 에너지 합은 일정하게 유지된다 (탄성 충돌).[3]

이러한 원리를 이용한 지상에서의 예시는 움직이는 기차 앞에서 테니스공이 튕기는 상황과 유사하다. 시속 30km/h로 움직이는 기차를 향해 시속 50km/h로 공을 던지면, 기차 운전사는 공이 시속 80km/h로 접근했다가 튕겨 나가는 것을 본다. 그러나 기차의 움직임 때문에, 정지한 관찰자에게는 공이 시속 130km/h로 튕겨 나가는 것으로 보인다. 즉, 공의 속도에 기차 속도의 두 배가 더해진 것이다.[4]

우주 공간에서 행성의 좌표계 기준으로 보면, 탐사선은 행성에 대해 수직 속도 ''v''로 접근한다. 스윙바이를 한 후에는 90도 각도로 멀어지며, 여전히 ''v''의 속도를 갖지만 방향은 수평이다.[2] 태양 기준 좌표계에서는 행성의 수평 속도 역시 v이므로, 피타고라스 정리에 따라 탐사선의 초기 속도는 ''v''이다. 스윙바이 후 탐사선의 속도는 ''v + v ='' 2''v''가 되어, 약 0.6''v''만큼 속도가 증가한다.[2]

이 설명은 에너지 보존 및 운동량 보존 법칙에 어긋나는 것처럼 보일 수 있지만, 탐사선이 행성에 미치는 영향도 고려해야 한다. 탐사선이 얻는 선형 운동량은 행성이 잃는 운동량과 크기가 같으므로, 탐사선은 속도를 얻고 행성은 속도를 잃는다. 그러나 행성의 질량이 탐사선에 비해 매우 크기 때문에, 행성의 속도 변화는 무시할 수 있을 정도로 작다.[5] 예를 들어, 목성의 질량은 1 미터톤인 탐사선보다 훨씬 큰 2 x 1024 미터톤 정도이다. 따라서 목성을 통과하는 1톤의 탐사선은 이론적으로 행성의 궤도 속도를 km/s당 약 5 x 10−25 km/s만큼 감소시킨다.[5]

궤도의 가역성 때문에 중력 슬링샷은 우주선의 속도를 줄이는 데에도 사용할 수 있다. 마리너 10호와 MESSENGER는 수성에 도달하기 위해 이 방법을 사용했다.

중력 보조 기동의 주요한 현실적인 제약은 행성들이 특정 목적지로 가는 데 적합한 위치에 있는 경우가 드물다는 것이다. 예를 들어, 1970년대 후반 보이저 임무는 목성, 토성, 천왕성, 해왕성의 "

또 다른 제약은 행성에 대기가 있을 경우이다. 우주선이 행성에 가까이 접근할수록 근점 속도가 빨라져 더 큰 중력 가속을 얻을 수 있지만, 너무 깊이 들어가면 대기 항력으로 인해 손실되는 에너지가 더 커질 수 있다.

JAXA의 하야부사 탐사선은 스윙바이를 위해 지구 근처 1km 범위 내를 속도 오차 1cm/s 이내로 통과하도록 궤도를 미세 조정했다. 궤도 조정에는 연료를 사용하며, 연료 소비를 최소화하고 지구와의 통신을 위한 안테나 방향을 유지하는 등의 조건도 고려해야 한다.

6. 주요 탐사선 적용 사례



1959년 루나 3호가 달의 뒷면을 촬영할 때 처음으로 스윙바이가 사용되었다.[17] 중력 보조 기동으로 궤도가 변경되어 사진을 성공적으로 전송할 수 있었다.[18] 이 기동은 므스티슬라프 켈디시의 지휘 하에 켈디시 응용수학 연구소에서 수행된 연구에 의존했다.[9][10][11][12]

  • '''파이오니어 10호'''


1972년 3월 2일 발사된 파이오니어 10호는 목성으로의 최초 임무를 완수한 우주 탐사선이다. 태양계를 벗어나기 위해 필요한 탈출 속도에 도달한 최초의 우주 탐사체로, 1973년 12월 스윙바이 항법을 사용했다.[19][20]

  • '''파이오니어 11호'''


1973년 NASA에 의해 발사된 파이오니어 11호는 소행성대, 목성 및 토성 주변 환경, 태양풍 및 우주선을 연구했다. 토성을 처음으로 조우하고, 소행성대를 두 번째로 통과했으며, 목성을 두 번째로 지나간 탐사선이었다. 토성에 도달하기 위해 목성에서 중력 보조를 받았다.[21][22][23]

  • '''마리너 10호'''


1974년 2월 5일, 마리너 10호 탐사선은 금성을 지나 수성을 탐사하기 위한 최초의 우주선이 되기 위해 중력 슬링샷 효과를 사용했다.[24]

1977년 9월 5일 NASA에 의해 발사된 보이저 1호는 목성과 토성 주변에서 슬링샷 기동을 수행하여 태양의 중력을 탈출할 에너지를 얻었다.[25] 심우주 네트워크와 통신하며 일상적인 명령을 수신하고 지구로 데이터를 전송한다. NASA와 JPL은 실시간 거리 및 속도 데이터를 제공한다.[26] 2020년 1월 12일 기준 지구에서 떨어진, 지구에서 가장 멀리 떨어진 인공 물체이다.[27][28]

1977년 8월 20일 NASA에 의해 발사된 보이저 2호는 외행성을 연구했다. 목성과 토성에 도달하는 데 쌍둥이 우주선보다 더 오래 걸렸지만, 천왕성과 해왕성과의 추가적인 조우를 가능하게 했다.[29]

1989년 NASA에 의해 발사된 갈릴레오 우주선은 목성으로 가는 경로에서 1990년 2월 10일 금성, 1990년 12월 8일과 1992년 12월 8일 지구에서 총 세 번의 중력 보조를 받았다. 1995년 12월에 목성에 도달했으며, 두 개의 소행성 243 이다와 951 가스프라를 통과했다.[30][31]

1990년 NASA는 ESA 우주선 ''율리시스''를 발사하여 태양의 극 지역을 연구했다. 1992년 2월 8일 목성으로부터의 중력 보조를 통해 태양 극 궤도 진입에 성공했다.[32][33]

2004년 8월 발사된 메신저 임무는 수성 궤도 진입 전에 속도를 늦추기 위해 지구 1회, 금성 2회, 수성 3회의 플라이바이를 포함하여 광범위하게 중력 보조를 사용했다. 2011년 3월 궤도 삽입에 성공했다.[34][35]

  • '''카시니'''


1997년 10월 15일 발사된 ''카시니-호이겐스'' 우주선은 금성(1998년 4월 26일 및 1999년 6월 21일), 지구(1999년 8월 18일), 목성(2000년 12월 30일)의 중력 보조 플라이바이를 거쳐 2004년 7월 1일 토성에 도착했다.[36][37] 2019년 "지금까지 실행된 가장 복잡한 중력 보조 궤도"라고 불렸다.[38]

토성 궤도 진입 후, ''카시니'' 우주선은 127번의 타이탄 중력 보조를 통해 궤도 경사를 크게 변경했다.[39] 타이탄 플라이바이는 레아 및 엔셀라두스와 같은 다른 위성을 통과할 수 있게 했다.

''로제타'' 궤도 애니메이션. 2004년 3월 2일부터 2016년 9월 9일까지


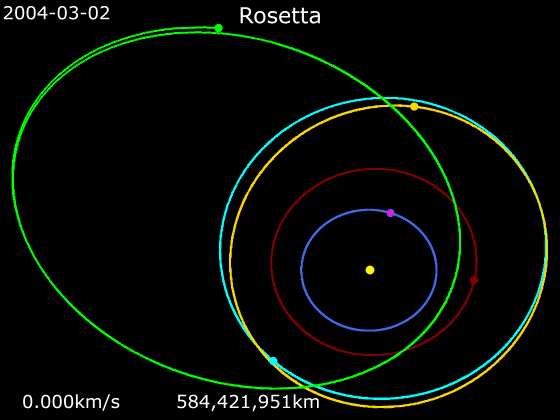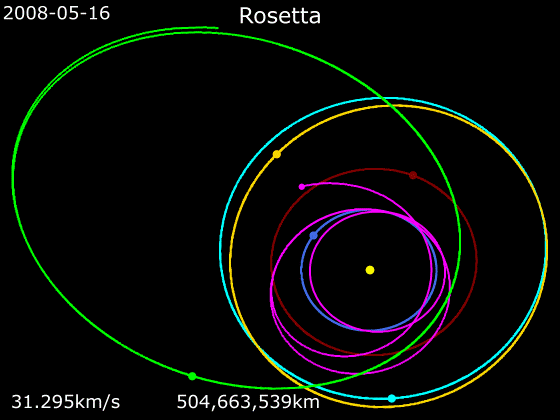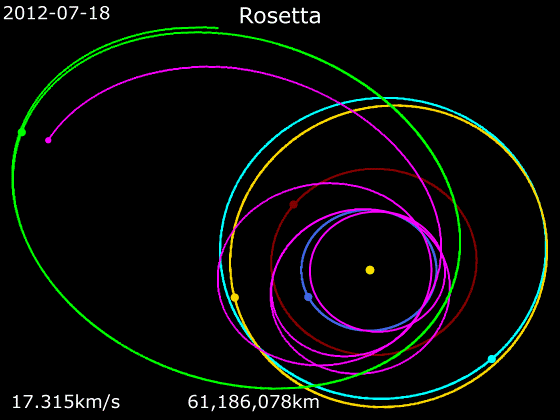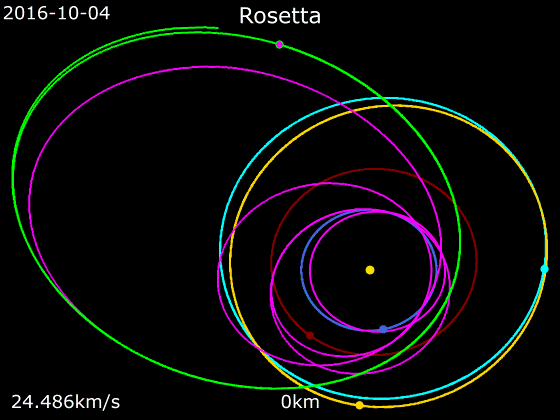
2004년 3월에 발사된 ''로제타'' 탐사선은 화성 표면에서 250km 떨어진 곳에서 한 번, 지구에서 세 번, 총 4번의 중력 보조 기동을 사용했다. 이를 통해 21 루테티아와 2867 슈테인스 소행성을 통과하고, 2014년 8월 67P/추류모프-게라시멘코 혜성의 속도와 일치할 수 있었다.[40][41]

  • '''뉴 호라이즌스'''


''뉴 호라이즌스''는 2006년 NASA에 의해 발사되어 2015년 명왕성에 도달했으며, 2007년 목성에서 중력 보조를 수행했다.[42][43]

2011년 8월 5일(UTC)에 발사된 주노 우주선은 2013년 10월 지구 플라이바이를 통해 중력 보조를 받아 5년 만에 목성을 향해 궤도와 속도를 변경했다.[44]

2018년 8월 7일부터 2025년 8월 29일까지의 파커 태양 탐사선 궤도 애니메이션


2018년 NASA에 의해 발사된 파커 태양 탐사선은 7번의 계획된 금성 중력 보조를 통해 태양에 근접한다. 2022년 현재 5번의 보조를 수행했다. 2024년 11월 6일 최종 중력 보조 기동으로 2024년 12월 24일 태양 표면에 근접할 예정이다.[45][46][47][48]

  • '''솔라 오비터'''


2020년 ESA에 의해 발사된 솔라 오비터는 2021년 11월까지 금성 2회, 지구 1회의 중력 보조 기동을 수행하여 태양계 안쪽으로 궤도를 변경했다. 첫 번째 근일점 통과는 2022년 3월 26일에 발생했다.[49]

베피콜롬보는 수성으로 가는 유럽 우주국 (ESA)과 일본 우주항공 연구 개발 기구 (JAXA)의 공동 임무로, 2018년 10월 20일에 발사되었다. 지구 1회, 금성 2회, 수성 6회의 중력 보조 기법을 사용하여 2025년에 도착할 예정이다.[50]

2021년 10월 16일 NASA에 의해 발사된 ''루시''는 2022년 10월 16일 지구에서 한 번, 2024년에 152830 딘키네시 소행성 플라이바이를 거쳐 또 한 번의 중력 보조를 받을 예정이다.[51][52] 2025년 52246 도널드존슨을 통과하고, 2027년 트로이 군에 도착하여 3548 유르바테스 등 여러 소행성을 탐사한다.[53][54] 2031년 지구로 돌아와 2033년 617 파트로클루스를 방문할 예정이다.

7. 허구 사례

다음은 여러 SF 작품에서 묘사된 스윙바이의 예시이다. 단, 이는 가상 설정이다.


  • 2001 스페이스 오디세이 (소설판): 우주선 디스커버리호는 목성에서 스윙바이를 통해 가속한 후 토성으로 향한다.
  • 2010 스페이스 오디세이: 우주선 레오노프호는 전방에 차열 벌룬을 전개하고, 목성 대기 마찰을 이용해 감속 스윙바이를 하여 목성 궤도에 진입한다.
  • 스타 트렉 4: 귀환의 길: 태양 중력을 이용한 슬링샷으로 시간 여행을 한다.
  • 우주전함 야마토 부활편: 아마르로 가는 제3차 이민선단이 블랙홀 중력을 이용하여 가속하고 워프를 한다.
  • 은하영웅전설 (애니메이션): 제50화. 라이갈·트리플 양 성역 회전에서 슈타인메츠 함대가 양 웬리가 지휘하는 이젤론 요새 주둔 함대(양 함대)의 중앙 돌파·배면 전개 전법에 의해 공수가 역전되어 블랙홀에 몰린다. 과감하게 응전하지만 양 함대의 맹공에 탈출하기 위해 슈바르츠실트 반지름에 가까이 접근하여 고속을 얻는 블랙홀 이용 스윙바이 항법을 실행한다. 함대는 스윙바이 실행 중 양 함대에 저격당하고 블랙홀에 다수의 함정이 삼켜지는 등 8할의 손해를 입었지만, 간신히 탈출에 성공한다.
  • 아마겟돈: 2기의 셔틀 (오비터, 인디펜던스와 프리덤)이 달 중력을 이용한 스윙바이로 가속하여 지구에 접근하는 소행성으로 향한다.
  • 브레멘 II: 폭발 직전 행성에서 탈출하기 위해, 엔진 불량을 보충하고자 스윙바이 항법으로 이탈한다. 작중에서는 이미 쇠퇴한 항법이며, "기술이 미발달했던 시대의 궁색한 절약 항법"이라고 칭해진다.
  • 인터스텔라: 엔듀런스가 블랙홀 중력을 이용한 스윙바이를 실행한다. 이에 따른 시간 지연은 51년이다.

참조

[1] 웹사이트 Section 1: Environment, Chapter 4: Trajectories https://solarsystem.[...] NASA 2018-07-21
[2] 웹사이트 Gravity assist http://www.planetary[...] The Planetary Society 2017-01-01
[3] 웹사이트 Let gravity assist you ... https://www.esa.int/[...] 2023-03-08
[4] 웹사이트 A Gravity Assist Primer https://solarsystem.[...] NASA 2018-07-21
[5] 간행물 The Slingshot Effect http://maths.dur.ac.[...] Durham University 2003-01
[6] 논문 Kondratyuk's paper
[7] 학술지 A historical review of the theory of gravity-assists in the pre-spaceflight era http://urlib.net/8JM[...] 2020-07-14
[8] 논문 Zander's 1925 paper
[9] 웹사이트 Mstislav Keldysh. Mechanics of the Space Flight http://www.keldysh.r[...] Keldysh Institute of Applied Mathematics
[10] 학술지 Specific problems of a flight to the moon 1957-09
[11] 서적 Essential Spaceflight Dynamics and Magnetospherics https://books.google[...] Kluwer Academic
[12] 웹사이트 All Hail Luna 3, Rightful King of 1950s Space Missions https://arstechnica.[...] 2023-10-13
[13] 웹사이트 The Maths That Made Voyager Possible https://www.bbc.com/[...] 2012-10-22
[14] 간행물 The Challenge of the Planets, Part Three: Gravity https://www.wired.co[...] 2022-12-05
[15] 웹사이트 Fast Reconnaissance Missions to the Outer Solar System Using Energy Derived from the Gravitational Field of Jupiter http://www.gravityas[...] 2024-01-06
[16] 학술지 Gravity Probe B: Final Results of a Space Experiment to Test General Relativity 2011-06
[17] 학술지 A historical review of the theory of gravity-assists in the pre-spaceflight era http://urlib.net/8JM[...] 2020-07-14
[18] 간행물 Simulation and Study of Gravity Assist Maneuvers http://www.diva-port[...] 2020
[19] 웹사이트 Let Gravity Assist You... https://www.scienced[...] 2022-12-05
[20] 서적 20th Annual Conference of Doctoral Students, WDS'11 "Week of Doctoral Students 2011", Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic, May 31, 2011 to June 3, 2011 : [proceedings of contributed papers]. Pt. 3 Physics https://www.mff.cuni[...] Matfyzpress 2022-12-05
[21] 웹사이트 Pioneer 11: In Depth https://solarsystem.[...] 2017-12-10
[22] 웹사이트 45 Years Ago, Pioneer 11 Explores Jupiter https://www.nasa.gov[...] 2019-12-02
[23] 웹사이트 Pioneer 10 and 11, outer solar system explorers https://www.planetar[...] 2022-12-05
[24] 웹사이트 In Depth {{!}} Mariner 10 https://solarsystem.[...] 2022-12-05
[25] 웹사이트 A Gravity Assist Primer https://solarsystem.[...] NASA 2018-07-21
[26] 웹사이트 Voyager - Mission Status https://voyager.jpl.[...]
[27] 웹사이트 Voyager – Mission Status https://voyager.jpl.[...] National Aeronautics and Space Administration 2019-12-26
[28] 웹사이트 Voyager 1 http://www.bbc.co.uk[...] 2018-09-04
[29] 서적 From Engineering Science to Big Science https://history.nasa[...] 2015-09-04
[30] 학술지 Galileo trajectory design 1992-05
[31] 웹사이트 Galileo Heads Towards Second Gravity Assist https://www.jpl.nasa[...] 2022-12-05
[32] 웹사이트 ESA Science & Technology - Orbit of Ulysses https://sci.esa.int/[...] 2022-12-05
[33] 웹사이트 ESA Science & Technology - Gravity Assist https://sci.esa.int/[...] 2022-12-05
[34] 웹사이트 MESSENGER – Unlocking the Mysteries of Planet Mercury https://messenger.jh[...] 2022-12-05
[35] 웹사이트 Resources / News Archives FLYBY INFORMATION https://messenger.jh[...] 2022-12-05
[36] 웹사이트 Cassini Trajectory https://solarsystem.[...] 2022-12-05
[37] 웹사이트 ESA Science & Technology – Getting to Saturn https://sci.esa.int/[...] 2022-12-05
[38] 서적 Space Operations: Inspiring Humankind's Future Springer International Publishing 2022-12-05
[39] 웹사이트 Gravity Assists {{!}} Mission https://solarsystem.[...] 2022-12-05
[40] 웹사이트 ESA Science & Technology – Rosetta Second Earth Swing-by https://sci.esa.int/[...] 2022-12-05
[41] 서적 2008 IEEE Aerospace Conference 2008-03-02
[42] 웹사이트 NASA – Grand Theft Pluto: New Horizons Gets a Boost From Jupiter Flyby https://www.nasa.gov[...] 2022-12-05
[43] 웹사이트 New Horizons Jupiter Flyby https://pds-atmosphe[...] 2022-12-05
[44] 웹사이트 NASA's Shuttle and Rocket Launch Schedule http://www.nasa.gov/[...] NASA 2011-02-17
[45] 웹사이트 Parker Solar Probe Completes Its Fifth Venus Flyby – Parker Solar Probe https://blogs.nasa.g[...] 2022-12-05
[46] 웹사이트 Parker Solar Probe Changed the Game Before It Even Launched https://www.nasa.gov[...] NASA 2022-12-05
[47] 간행물 Execution of Parker Solar Probe's unprecedented flight to the Sun and early results 2021-02-01
[48] 웹사이트 NASA’s Sun-Bound Parker Solar Probe Swings Through Final Venus Flyby {{!}} Johns Hopkins University Applied Physics Laboratory https://www.jhuapl.e[...] 2024-12-19
[49] 웹사이트 GMS: Solar Orbiter's Orbit https://svs.gsfc.nas[...] 2020-02-14
[50] 웹사이트 ESA Science & Technology BepiColombo https://sci.esa.int/[...] 2022-06-28
[51] 웹사이트 Lucy completes its first Earth gravity assist after a year in space https://www.nasaspac[...] NASA Spaceflight.com 2022-10-24
[52] 웹사이트 NASA Awards Launch Services Contract for Lucy Mission https://www.nasa.gov[...] NASA 2021-03-29
[53] 뉴스 NASA announces five Discovery proposals selected for further study http://www.planetary[...] The Planetary Society 2015-09-30
[54] 뉴스 A Metal Ball the Size of Massachusetts That NASA Wants to Explore https://www.nytimes.[...] 2017-01-06
[55] 문서 "スイングバイ(かすめ飛行)の理解へ向けて:Voyager号の運動を試すモデル・ソフトウェアの作成" http://www.nhao.jp/r[...] 兵庫県立西はりま天文台年報 1998-03-31
[56] 문서 ただし、一般に天体の質量のほうが何倍も大きいので、天体側の運動ベクトルの変化は誤差の範囲である。
[57] 문서 Venus-Earth-Earth gravity assist


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com