스토크스 현상

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 스토크스 곡선과 반-스토크스 곡선
4. 예
- 4.1. 에어리 함수
- 4.2. 2차 선형 미분 방정식
5. 역사
참조

1. 개요

스토크스 현상은 전해석 함수가 아닌 함수로 근사될 때 나타나는 현상으로, 지수적으로 작은 항이 스토크스 곡선을 가로지를 때 다른 지수적으로 작은 항을 켜거나 끄는 방식으로 동작한다. 이 현상은 점근적 전개의 발산과 관련이 있으며, 팩토리얼-오버-파워 발산 형태를 보인다. 스토크스 곡선은 $\Im\{\chi\}=0$ 및 $\Re\{\chi\}>0$ 조건을, 반-스토크스 곡선은 $\Re\{\chi\}=0$ 조건을 만족하여 결정된다. 에어리 함수는 스토크스 현상의 대표적인 예시이며, 2차 선형 미분 방정식의 해를 구할 때 WKB 방법을 사용하여 스토크스 현상을 관찰할 수 있다. 이 현상은 조지 가브리엘 스토크스가 에어리 함수를 연구하면서 처음 발견했다.

더 읽어볼만한 페이지

점근 해석 - 마스터 정리
마스터 정리는 분할 정복 알고리즘의 시간 복잡도 분석 도구로서, 점화식을 세 가지 경우로 나누어 재귀 알고리즘의 효율성을 파악하고, 다양한 정렬 및 일반 알고리즘 분석에 활용되지만, 특정 조건에서는 적용이 제한될 수 있습니다.
점근 해석 - 섭동 이론
섭동 이론은 정확히 풀리는 문제에 작은 변화가 있을 때 급수로 표현하여 근사해를 구하는 방법으로, 초기 해에 보정항을 더하는 방식으로 고전역학, 양자역학 등 다양한 분야에서 활용되며 섭동 형태와 적용 차수에 따라 구분된다.
복소해석학 - 선적분
선적분은 스칼라장이나 벡터장의 곡선에 대한 적분으로, 함수의 종류와 곡선의 표현 방식에 따라 다양하게 정의되며, 물리학과 공학 등에서 활용된다.
복소해석학 - 테일러 급수
테일러 급수는 매끄러운 함수를 무한 멱급수로 나타내는 방법으로, 함수의 미분 계수를 사용하여 함수를 근사하며, a=0일 때의 테일러 급수를 매클로린 급수라고 한다.

스토크스 현상
개요
유형	수학적 특이 현상
분야	점근 해석, 미분 방정식
관련 개념	특이 섭동 이론, 점근 급수
설명
내용	스토크스 현상은 미분 방정식의 해나 점근 급수의 계수와 같은 특정 함수의 점근적 거동이 복소 평면의 특정 방향(스토크스 선)을 가로지를 때 급격하게 변하는 현상이다.
원인	작은 항이 무시할 수 없게 되어 해의 지배적인 균형에 영향을 미쳐 선형 미분 방정식에서 해의 점근적 근사의 계수에서 불연속적인 변화를 일으킨다.
특징	선형 미분 방정식의 해의 점근 해석에서 스토크스 선을 가로지를 때, 점근 급수에서 작은 항의 계수가 급격하게 변한다. 이 현상은 점근 해의 우세도 사이의 균형이 깨지면서 발생한다.
역사적 배경
발견자	조지 가브리엘 스토크스 경
최초 관찰	1847년, 에어리 함수 연구 중
추가 연구	스토크스 현상에 대한 엄밀한 수학적 설명은 스토크스 (G. G. Stokes, 1858)에 의해 제공되었으며, 이후 다른 수학자들에 의해 더욱 발전되었다.
응용
분야	물리학 수학
세부 분야	특이 섭동 이론 점근 해석
추가 정보
관련 항목	스토크스 선 스토크스 상수

2. 정의

어떤 전해석 함수 $f\colon\mathbb C\to\mathbb C$ 가 $|z|\gg1$ 에 대하여 다음과 같이 근사된다고 하자.

: $f(z)\approx g(z)\qquad(|z|\gg1)$

여기서 $g(z)$ 는 전해석 함수가 아니며, 분지절단을 가질 수 있다. 이 경우, $f$ 가 '''스토크스 현상'''을 보인다고 한다.

3. 스토크스 곡선과 반-스토크스 곡선

어떤 전해석 함수 $f\colon\mathbb C\to\mathbb C$ 가 $|z|\gg1$ 에 대하여 다음과 같이 근사된다고 하자.

: $f(z)\approx g(z)\qquad(|z|\gg1)$

여기서 $g(z)$ 는 전해석 함수가 아니며, 분지절단을 가질 수 있다. 이 경우, $f$ 가 '''스토크스 현상'''을 보인다고 한다.

일반적으로 점근적 근사는 여러 개의 점근적 항으로 구성되어 있다. 대부분의 편각에서는 이 항 가운데 하나만이 지수적으로 우세하게 되고, 따라서 나머지 항들은 버릴 수 있다. 여러 항들의 크기가 일치하게 되는 점들을 '''반 스토크스 선'''(anti-Stokes line^영어)이라고 한다. 이러한 점에서는 점근적 근사의 우세한 항이 바뀌게 된다.

열등한 항의 계수는 '''스토크스 선'''(Stokes line^영어)에서 급격한 변화를 겪는다. 스토크스 선은 우세한 항이 열등한 항보다 상대적으로 가장 큰 값을 갖는 선이다.

에어리 함수 $\operatorname{Ai}(z)$ 의 스토크스 선들은

: $\operatorname{arg}(z)=2n\pi/3\qquad(n\in\mathbb Z)$

이며, 반 스토크스 선들은

: $\operatorname{arg}(z)=(2n+1)\pi/3\qquad(n\in\mathbb Z)$

이다.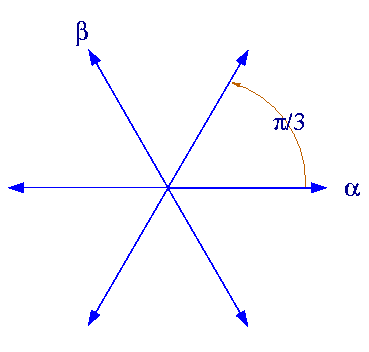

스토크스 곡선을 가로질러 지수적으로 작은 항이 다른 지수적으로 작은 항을 켜거나 끌 수 있다.

반-스토크스 곡선을 가로질러, 지배적이지 않은 지수적으로 작은 항은 지배적인 지수적으로 큰 항으로 전환될 수 있으며 그 반대의 경우도 가능하다.

스토크스 및 반-스토크스 곡선에서 이러한 동작의 변화는 점근적 전개의 발산과 직접적으로 관련이 있다.

스토크스 곡선은

\Im\{\chi\}=0

및

\Re\{\chi\}>0

조건을 사용하여 결정된다. 반-스토크스 곡선은

\Re\{\chi\}=0

조건을 사용하여 결정된다.

예를 들어, ''x''의 극한을 크고 실수를 고려하고, 양수와 음수 값 모두에 대해 에어리 함수를 근사하려는 경우, ''x''의 인수를 0에서 π로 증가시키면서 (위쪽 절반 복소 평면을 통해 회전시키면서), 우리는 반-스토크스 선을 넘어선 것이다. 이 경우 반-스토크스 선은

\operatorname{arg}\, x = \pi / 3

에 있다.

인수가 π/3, π, –π/3인 세 개의 반-스토크스 선과 인수가 2π/3, 0, –2π/3인 세 개의 스토크스 선이 있다.

4. 예

일반적으로 점근적 근사는 여러 개의 점근적 항으로 구성되어 있다. 대부분의 편각에서는 이 항 가운데 하나만이 지수적으로 우세하게 되고, 따라서 나머지 항들은 버릴 수 있다. 여러 항들의 크기가 일치하게 되는 점들을 '''반 스토크스 선'''(anti-Stokes line^영어)이라고 한다. 이러한 점에서는 점근적 근사의 우세한 항이 바뀌게 된다.

열등한 항의 계수는 '''스토크스 선'''(Stokes line^영어)에서 급격한 변화를 겪는다. 스토크스 선은 우세한 항이 열등한 항보다 상대적으로 가장 큰 값을 갖는 선이다.

에어리 함수와 2차 선형 미분 방정식의 예시를 통해 스토크스 현상을 설명할 수 있다.

4. 1. 에어리 함수

에어리 함수

\operatorname{Ai}(z)

는

\widehat\infty

에서 본질적 특이점을 갖는 전해석 함수이다. 임의의 편각

\operatorname{arg}z

에 대하여, 에어리 함수는 다음과 같이 근사된다.

:

\operatorname{Ai}(z)\sim C_+x^{-1/4}\exp(+(2/3)x^{3/2})+C_-x^{-1/4}\exp(-(2/3)x^{3/2})

이 근삿값은 전해석 함수가 아니므로, 스토크스 현상이 발생하는 것을 볼 수 있다.

\operatorname{Ai}(z)

의 스토크스 선들은

:

\operatorname{arg}(z)=2n\pi/3\qquad(n\in\mathbb Z)

이며, 반 스토크스 선들은

:

\operatorname{arg}(z)=(2n+1)\pi/3\qquad(n\in\mathbb Z)

이다. 스토크스 선 근처에서

C_+

와

C_-

의 값은 급격히 변할 수 있다.

에어리 함수 Ai(''x'')는 다음과 같은 간단한 미분 방정식의 두 해 중 하나이다.

:

y'' - xy = 0 , \,

이는 복소수를 포함하여, 많은 ''x'' 값에 대해 근사하는 것이 종종 유용하다. 주어진 인수가 큰 ''x''의 경우, 해는 다음 함수의 선형 결합으로 근사할 수 있다.

:

\frac{e^{\pm\frac23x^{3/2}}}{x^{1/4}}.

하지만, 선형 결합은 ''x''의 인수가 특정 값을 지날 때 (''x''가 가지 절단을 가로지를 때) 변경되어야 한다. 이러한 근사값에는 다중 값 함수가 포함되어 있기 때문이다. 반면에, 에어리 함수는 단일 값을 가지며 실제로 정함수이므로, 근사를 이해하려면 여러 가능한 값 중에서 단일 값을 선택해야 한다 (이는 암묵적으로 근사에 대한 가지 절단을 부과한다).

예를 들어, ''x''의 극한을 크고 실수를 고려하고, 양수와 음수 값 모두에 대해 에어리 함수를 근사하려는 경우, 다음을 찾을 수 있다.

right

:

\begin{align}\mathrm{Ai}(x) &{}\sim \frac{e^{-\frac23x^{3/2}}}{2\sqrt\pi\,x^{1/4}} \\\mathrm{Ai}(-x) &{}\sim \frac{\sin(\frac23x^{3/2}+\frac14\pi)}{\sqrt\pi\,x^{1/4}} \\\end{align}

이 두 식은 매우 다르다. ''x''의 인수를 0에서 π로 증가시키면서 (위쪽 절반 복소 평면을 통해 회전시키면서), 반-스토크스 선을 넘어선 것이다. 이 경우 반-스토크스 선은

\operatorname{arg}\, x = \pi / 3

에 있다. 이 반-스토크스 선에서,

\frac{e^{-\frac23x^{3/2}}}{x^{1/4}}

의 계수는 강제로 점프한다.

\frac{e^{+\frac23x^{3/2}}}{x^{1/4}}

의 계수는 이 선에서 점프할 수 있지만, 강제되지는 않는다. 이 영역에서는 결정되지 않으므로, arg ''x''가 π/3에서 π로 변함에 따라 점차적으로 변경될 수 있다.

인수가 π/3, π, –π/3인 세 개의 반-스토크스 선과 인수가 2π/3, 0, –2π/3인 세 개의 스토크스 선이 있다.

4. 2. 2차 선형 미분 방정식

변수의 표준적인 변화를 통해, 2차 선형 미분 방정식은 종종 다음 형태로 변경될 수 있다.

:

\frac{d^2w}{dz^2} = f(z)w

여기서 ''f''는 단일 연결 영역에서 정칙이며 ''w''는 미분 방정식의 해이다. 어떤 경우에는 WKB 방법이 다음과 같은 형태의 함수의 선형 결합으로 ''w''에 대한 점근 근사를 제공한다.

:

\frac{e^{\pm\int_a^z\sqrt{f(z')} \, dz'}}{f(z)^{1/4}}

어떤 상수 ''a''에 대해. (다른 ''a'' 값을 선택하는 것은 선형 결합에서 다른 계수를 선택하는 것과 같다.) 그러면 반-스토크스 선과 스토크스 선은 각각

:

\int_a^z\sqrt{f(z')} \, dz'.

의 실수부와 허수부의 영점이다.

만약 ''a''가 ''f''의 단순한 영점이라면, 국소적으로 ''f''는

f'(a)(z-a)

와 같다. 해는 국소적으로 에어리 함수와 같이 동작할 것이다. 즉, ''a''에서 만나는 세 개의 스토크스 선과 세 개의 반-스토크스 선을 가질 것이다.

5. 역사

조지 가브리엘 스토크스가 에어리 함수를 연구하는 과정에서 발견하였다.^[1]^[2]^[3]

참조

_[1] 저널 On the numerical Calculation of a Class of Definite Integrals and Infinite Series http://biodiversityl[...] 1851
_[2] 저널 On the Discontinuity of Arbitrary Constants which appear in Divergent Developments http://biodiversityl[...] 1858
_[3] 저널 Supplement to a paper on the Discontinuity of Arbitrary Constants which appear in Divergent Developments 1869

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com