맨위로가기

영상 정합

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

영상 정합은 여러 영상 간의 대응 관계를 찾아 공간적으로 일치시키는 기술이다. 알고리즘은 세기(강도) 기반과 특징 기반으로 나뉘며, 변환 모델에 따라 선형 변환, 비강체 변환 등으로 분류된다. 공간 영역과 주파수 영역 방식이 있으며, 단일 모달리티 및 다중 모달리티 영상 정합이 가능하다. 유사성 척도를 통해 영상 간의 유사성을 측정하며, 불확실성을 고려해야 한다. 의료 영상, 원격 탐사, 컴퓨터 비전 등 다양한 분야에 응용되며, 자동화 수준에 따라 수동, 대화형, 반자동, 자동 방식으로 구분된다.

더 읽어볼만한 페이지

  • 컴퓨터 비전 - 합성곱 신경망
    합성곱 신경망(CNN)은 이미지, 영상 등 시각 데이터 처리에 특화된 인공 신경망으로, 합성곱층, 풀링층, 완전 연결층으로 구성되어 특징 추출, 차원 축소, 최종 분류 또는 예측을 수행하며 이미지 인식, 영상 분석, 자연어 처리 등 다양한 분야에 응용된다.
  • 컴퓨터 비전 - 광학 흐름
    광학 흐름은 비디오나 이미지에서 보이는 객체, 표면, 엣지의 움직임 패턴을 나타내며, 움직임 예측, 비디오 압축, 장면 구조 추정, 로봇 내비게이션 등 다양한 분야에 활용되는 중요한 기술이다.
영상 정합

2. 알고리즘 분류

영상 정합 알고리즘은 다양한 기준에 따라 분류할 수 있다.


  • 세기(강도) 기반 vs 특징 기반: 영상의 밝기 패턴을 직접 비교하는 세기 기반 방법과 특징점을 추출하여 대응 관계를 찾는 특징 기반 방법으로 나뉜다. 이 두 방법은 상호 보완적으로 사용될 수 있다.
  • 변환 모델: 적용되는 변환 모델에 따라 선형 변환과 비강체 변환(탄성 변환)으로 분류할 수 있다. 선형 변환은 전역적인 기하학적 변환을 모델링하고, 비강체 변환은 국소적인 변형을 허용한다.
  • 좌표 변환 방식: 전산 해부학 분야에서는 호메오모피즘과 미분동형사상을 기반으로 하는 고급 방법들이 사용된다. LDDMM[7][8][9][10]은 궤적 흐름의 전산 해부학에 해당하는 좌표계를 연결하는 주요 도구이다.
  • 공간 영역 vs 주파수 영역: 공간 영역 방식은 픽셀 값이나 특징점을 직접 이용하고, 주파수 영역 방식은 푸리에 변환 등을 이용하여 주파수 영역에서 변환 매개변수를 찾는다. 위상 상관 방법은 주파수 영역 방식의 한 예시이다.
  • 단일 모달리티 vs 다중 모달리티: 촬영 방식에 따라 동일한 종류의 영상들을 정합하는 단일 모달리티 정합과 서로 다른 종류의 영상들을 정합하는 다중 모달리티 정합으로 나뉜다. 다중 모달리티 정합은 의료 영상 분야에서 활발하게 사용된다.
  • 자동화 수준: 자동화 단계에 따라 수동, 대화형, 반자동, 자동 방식으로 나눌 수 있다.

2. 1. 세기(강도) 기반 vs 특징 기반

영상 정합 알고리즘은 크게 세기(강도) 기반 방법과 특징 기반 방법으로 나뉜다.[3] 세기 기반 방법은 영상의 세기 패턴을 직접 비교하는 반면, 특징 기반 방법은 영상에서 점, 선, 윤곽선 등 특징점을 추출하여 이들 간의 대응 관계를 찾는다.[3]

세기 기반 방법은 주로 상관관계 지표를 사용하며, 전체 영상 또는 부분 영상을 대상으로 정합한다.[3] 부분 영상을 정합하는 경우, 해당 부분 영상의 중심을 대응 특징점으로 간주한다. 특징 기반 방법은 이미지 내의 여러 특징점들 간의 대응 관계를 설정한다.[3] 이를 통해 기하학적 변환을 결정하여 타겟 이미지를 기준 이미지에 매핑함으로써 두 이미지 간의 점대점 대응 관계를 설정할 수 있다.[3]

두 방법은 상호 보완적으로 사용될 수 있으며, 강도 기반 정보와 특징 기반 정보를 결합하는 방법도 개발되었다.[4]

2. 2. 변환 모델

영상 정합 알고리즘은 적용되는 변환 모델에 따라 분류할 수 있다.

  • '''선형 변환''': 이동, 회전, 크기 변환, 아핀 변환 등 전역적인 기하학적 변환을 모델링한다.[5] 그러나 선형 변환은 영상 간의 국소적인 기하학적 차이를 표현하기 어렵다.[3]

  • '''비강체 변환 (탄성 변환)''': 국소적인 변형을 허용한다. 방사 기저 함수(얇은 판 또는 표면 스플라인, 멀티쿼드릭, 컴팩트 지원 변환[3]), 물리적 연속체 모델(점성 유체), 대변형 모델(미분동형 사상) 등을 포함한다.


변환은 매개변수의 유무에 따라 분류할 수도 있다.

  • '''매개변수 모델''': 변환을 설명하는 매개변수가 존재한다. 예를 들어, 전체 이미지의 이동은 단일 매개변수인 이동 벡터로 설명할 수 있다.
  • '''비매개변수 모델''': 매개변수화를 따르지 않으며, 각 이미지 요소가 임의로 이동될 수 있도록 한다.[6]


변형 필드의 추정 및 적용을 구현하는 프로그램에는 SPM 및 AIR 등이 있다.

2. 3. 좌표 변환 방식

공간 정규화를 위한 고급 방법들은 변환 과정에서 매끄러운 부분다양체를 유지하기 위해 호메오모피즘과 미분동형사상을 기반으로 한다. 미분동형사상은 전산 해부학 분야에서 덧셈 방식이 아닌 함수 합성 법칙에 따라 그룹을 형성하며, 흐름(flow)을 기반으로 생성된다. 이러한 흐름은 위상을 보존하는 큰 변형을 생성하여 일대일 대응(1-to-1) 및 onto 변환을 가능하게 한다.

이러한 변환을 생성하는 계산 방법으로는 LDDMM[7][8][9][10]이 대표적이며, 이는 궤적 흐름의 전산 해부학에 해당하는 좌표계를 연결하는 주요 도구로 활용된다.

미분동형 사상을 통해 좌표의 미분동형 변환을 생성하는 프로그램에는 MRI Studio[11]와 MRI Cloud.org[12]가 있다.

2. 4. 공간 영역 vs 주파수 영역

공간 영역 방식은 영상의 픽셀 값이나 특징점을 직접 이용하여 정합을 수행한다. 특징점 정합은 사람이 직접 영상 속 특징점을 맞추는 수동 영상 정합을 자동화한 방식이다. 두 영상 속 특징점 쌍의 개수가 영상 변형에 필요한 최소 개수보다 많으면, RANSAC과 같은 알고리즘을 통해 두 영상 사이의 변형을 찾아낼 수 있다.[13][14]

주파수 영역 방식은 푸리에 변환 등을 이용하여 주파수 영역에서 변환 매개변수를 찾는다. 이 방법으로 영상의 이동, 회전, 크기 변화 등을 찾아낼 수 있다. 위상 상관 방법은 한 쌍의 영상에 적용하면 단일 피크를 갖는 세 번째 영상을 생성하는데, 이 피크의 위치가 영상 간의 상대적 이동을 나타낸다. 주파수 영역 방식은 잡음, 폐색 등에 강하며, 고속 푸리에 변환을 통해 효율성을 높일 수 있다. 또한, 영상의 로그-극좌표 변환을 통해 회전 및 크기 조정 차이를 결정할 수 있다.[13][14]

2. 5. 단일 모달리티 vs 다중 모달리티

영상 정합은 촬영 방식에 따라 단일 모달리티 정합과 다중 모달리티 정합으로 나눌 수 있다. 단일 모달리티 정합은 동일한 종류의 스캐너나 센서로 촬영한 영상들을 정합하는 방식이다. 반면, 다중 모달리티 정합은 서로 다른 종류의 스캐너나 센서로 촬영한 영상들을 정합하는 방식이다.[3]

다중 모달리티 정합은 특히 의료 영상 분야에서 활발하게 사용된다. 환자의 신체 영상을 서로 다른 스캐너를 통해 얻는 경우가 많기 때문이다. 예를 들어, 자기공명영상(MRI)과 컴퓨터 단층촬영(CT) 영상을 결합하거나, 양전자 방출 단층촬영(PET)과 CT 영상을 결합하여 종양의 위치를 정확하게 파악할 수 있다. 또한, 초음파 영상과 CT 영상을 결합하여 방사선 치료 시 전립선의 위치를 찾는 데 활용하기도 한다.[15]

2. 6. 자동화 수준

영상 정합은 자동화 단계에 따라 수동, 대화형, 반자동, 자동 방식으로 나눌 수 있다.

  • 수동 방식: 사용자가 도구를 이용해 맞춰야 할 영상을 참조 영상에 직접 정렬한다.
  • 대화형 방식: 사용자가 대략적으로 지시하면, 컴퓨터가 자동으로 영상을 정합한다.
  • 반자동 방식: 컴퓨터가 대부분의 정합 과정을 수행하고, 사용자는 결과를 검토한다.
  • 자동 방식: 사용자의 도움 없이 컴퓨터가 모든 정합 과정을 수행한다.

3. 유사성 척도

영상 정합의 정확도를 평가하기 위해 두 영상 간의 유사성을 측정하는 척도가 사용된다. 어떤 유사성 척도를 이용할지는 어떤 영상 방식을 이용하느냐에 따라 다르다.

서로 다른 영상 방식(다중 모달리티 정합) 간의 정합을 위해서는 상호정보량, 정규상호정보량 등이 주로 사용된다.[3] 같은 방식의 영상(단일 모달리티 정합) 간의 정합에는 상관계수, 차 제곱합 등이 사용될 수 있다.[3]

영상 유사성은 의료 영상 분야에서 광범위하게 사용된다. 영상 유사성 측정은 두 영상의 강도 패턴 간의 유사성 정도를 정량화한다.[3] 상호 정보량과 정규화된 상호 정보량은 다중 모드 영상 등록에 가장 널리 사용되는 영상 유사성 측정 방법이다.[3] 상호 상관, 제곱 강도 차이의 합 및 비율 영상 균일성은 동일한 모드 내의 영상 등록에 일반적으로 사용된다.[3]

전산 해부학 분야에서는 대응 관계가 없는 점 집합 또는 랜드마크인 측정 매칭, 수학적 전류 및 변형을 통한 곡선 매칭 및 표면 매칭 등의 방법론이 연구되고 있다.

4. 불확실성

영상 정합에는 시공간적 차이가 있는 이미지들을 정합하는 것과 관련된 일정 수준의 불확실성이 존재한다. 불확실성 측정을 포함하는 신뢰할 수 있는 정합은 의료 영상에서 환부의 변화를 감지하는 변화 탐지 응용 분야와 같이 매우 중요하다.[16][17]

원격 감지 응용 분야(예: 미국 항공 우주국(NASA)의 LANDSAT 영상)에서, 디지털 이미지 픽셀이 여러 킬로미터의 공간적 거리를 나타낼 수 있다. 이러한 환경에서 불확실한 이미지 정합은 해결책이 실제 위치와 수 킬로미터 떨어져 있을 수 있음을 의미할 수 있다. 여러 주요 논문에서 결과를 비교하기 위해 영상 정합의 불확실성을 정량화하려고 시도했다. 그러나 불확실성을 정량화하거나 변형을 추정하는 많은 접근 방식은 계산 집약적이거나 제한된 일련의 공간 변환에만 적용할 수 있다.[16][17]

5. 응용

영상 정합은 다양한 분야에 응용된다.


  • '''의료 영상''': 동일 환자의 서로 다른 시점에 촬영된 데이터를 정합하여 변화를 감지하거나 종양을 추적 관찰한다. 또한, CT, MRI, PET 등 서로 다른 영상 양식 간 정합을 통해 진단의 정확성을 높인다. 환자 데이터를 탈라이라크 아틀라스와 같은 해부학적 아틀라스에 정합하는 데에도 활용된다. 이러한 정합에는 대상의 변형(호흡, 해부학적 변화 등)을 처리하기 위해 ''탄성''(비강체) 정합이 추가로 포함되기도 한다.[18][19][20]

뇌의 두 MRI 영상 정합

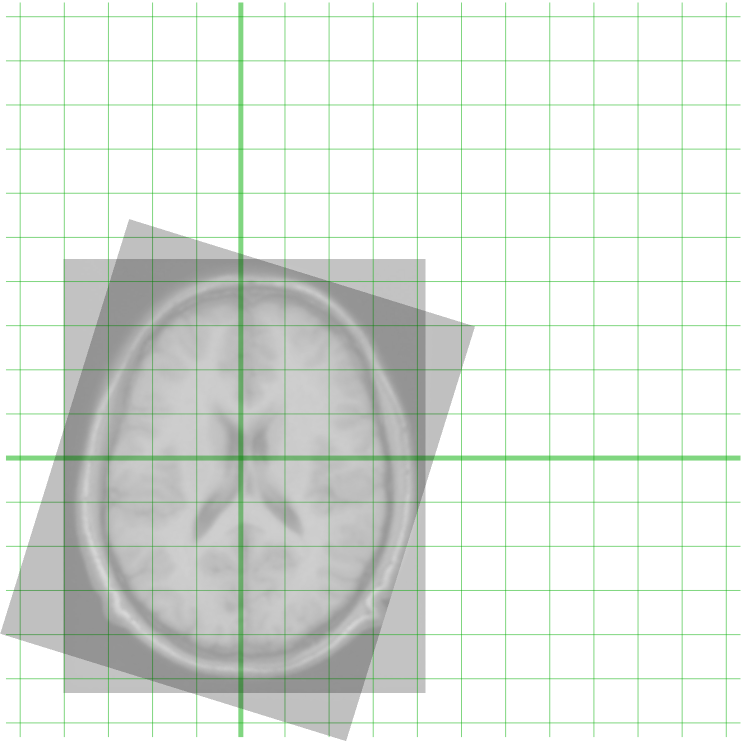
  • '''원격 탐사''': 지도 제작 및 갱신에 활용된다.
  • '''컴퓨터 비전''': 자율주행, 로봇, 증강현실 등 다양한 분야에서 객체 인식, 3차원 복원 등을 위해 활용된다.
  • '''천체 사진''': 영상 정렬 및 적층을 통해 흐릿한 천체 이미지의 신호 대 잡음비를 높여 품질을 개선한다. 행성 자전이나 태양 횡단과 같은 사건의 타임랩스 영상을 제작하는 데에도 사용된다. 제어점을 사용하여 한 이미지에 변환을 수행함으로써, 서로 다른 크기나 다른 망원경/렌즈로 촬영된 이미지들을 결합할 수 있다.
  • '''극저온 투과 전자 현미경''': 시료 드리프트를 보정하여 고해상도 이미지를 얻는 데 사용된다. 낮은 신호 대 잡음비(SNR) 데이터의 경우, 이미지 스택의 모든 이미지 순열을 교차 상관하여 최적의 영상 정합을 수행한다.[21]
  • '''파노라마 이미지 생성''': 여러 장의 이미지를 이어 붙여 파노라마 이미지를 만드는 데 필수적인 기술이다. 카메라 및 스마트폰과 같은 장치에서 실시간으로 구현되는 다양한 기술이 존재한다.


하지만 영상 정합은 적용 분야가 매우 광범위하므로, 모든 경우에 최적화된 일반적인 방법을 개발하는 것은 불가능하다.

참조

[1] 논문 A survey of image registration techniques http://portal.acm.or[...] ACM Computing Surveys archive 1992-12
[2] 웹사이트 biological imaging and brain mapping http://www.nature.co[...]
[3] 서적 2-D and 3-D Image Registration for Medical, Remote Sensing, and Industrial Applications http://www.wiley.com[...] Wiley Press 2005
[4] 서적 Medical Image Computing and Computer-Assisted Intervention – MICCAI 2004
[5] PDF http://www.comp.nus.[...] 2022-03
[6] 간행물 Deformable Medical Image Registration: A Survey https://hal.inria.fr[...] 2013-07
[7] 서적 Brain Warping https://books.google[...] Academic Press 1998-11-17
[8] 웹사이트 Landmark matching on brain surfaces via large deformation diffeomorphisms on the sphere — University of Utah https://web.archive.[...] 2016-03-21
[9] 간행물 Computing Large Deformation Metric Mappings via Geodesic Flows of Diffeomorphisms https://www.research[...] 2016-03-21
[10] 간행물 Landmark matching via large deformation diffeomorphisms 2000-01-01
[11] 웹사이트 MRI Studio https://www.mristudi[...]
[12] 웹사이트 MRICloud Brain Mapping https://mricloud.org[...]
[13] 간행물 An FFT-Based Technique for Translation, Rotation and Scale-Invariant Image Registration 1996-08
[14] 논문 Image Registration Using Log-Polar Mappings for Recovery of Large-Scale Similarity and Projective Transformations https://www-cs.ccny.[...] 2005-10
[15] 간행물 Cy Tran': A cycle-consistent transformer with multi-level consistency for non-contrast to contrast CT translation
[16] 논문 A Statistics Based Approach to Binary Image Registration with Uncertainty Analysis 2007-01
[17] 학회자료 Parametric estimation of affine deformations of binary images 2008
[18] 간행물 Unsupervised 3D End-to-End Medical Image Registration With Volume Tweening Network https://ieeexplore.i[...]
[19] arXiv ViT-V-Net: Vision Transformer for Unsupervised Volumetric Medical Image Registration 2021-04-13
[20] 서적 2021 IEEE International Conference on Image Processing (ICIP)
[21] 간행물 Image registration of low signal-to-noise cryo-STEM data


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com