영의 부등식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

영의 부등식은 음이 아닌 실수 a와 b, 그리고 1/p + 1/q = 1을 만족하는 양의 실수 p, q에 대해 성립하는 부등식으로, ab ≤ a^p/p + b^q/q 형태로 표현된다. 이 부등식은 횔더 부등식을 증명하는 데 사용되며, 로그 함수의 오목성, 젠센 부등식, 그리고 횔더 지수와 같은 다양한 수학적 개념과 연관되어 있다. 또한, 2를 지수로 갖는 초등적 형태, 증가 함수를 이용한 일반화, 펜켈-르장드르 변환을 이용한 일반화, 행렬 형태, 합성곱 형태 등 다양한 형태로 일반화될 수 있다.

더 읽어볼만한 페이지

부등식 - 구매력 평가
구매력 평가는 일물일가의 법칙에 기반하여 국가 간 물가 수준을 비교하고 환율을 계산하는 경제 이론으로, GDP 비교나 환율 예측 등에 활용되지만 여러 한계점도 존재한다.
부등식 - 불확정성 원리
불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리로, 입자의 위치와 운동량 등 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것이 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다.
대수학 - 다항식
다항식은 변수, 계수, 상수항으로 구성되어 덧셈, 뺄셈, 곱셈, 거듭제곱 연산으로 결합된 항들의 유한한 합으로 표현되는 식이며, 대수 방정식 해를 구하는 데 중요하고 현대 수학에서 폭넓게 활용된다.
대수학 - 상수
상수는 변하지 않는 일정한 값을 가지는 수로, 함수에서 변수와 대비되며 수식 내에서 고정된 값을 갖고, 원주율, 자연로그의 밑, 허수 i 등이 대표적인 예시이다.
해석학 (수학) - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.
해석학 (수학) - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.

영의 부등식
개요
이름	영의 부등식 (곱셈)
영어 이름	Young's inequality for products
일본어 이름	積に対するヤングの不等式 (세키니 타이 스루 얀구노 부토시키)
분야	실해석학, 함수해석학
관련 인물	윌리엄 헨리 영
공식
일반적인 형태	a, b, p, q > 1이고, 1/p + 1/q = 1일 때, 다음이 성립한다. ab ≤ a^p/p + b^q/q
함수 형태	f와 g가 [0, 1]에서 정의된 연속 증가 함수이고 f(0) = 0, g(0) = 0이며, f와 g가 서로 역함수 관계에 있을 때, 모든 a ≥ 0 및 b ≥ 0에 대해 다음이 성립한다. ab ≤ ∫0^a f(x) dx + ∫0^b g(y) dy
조건	f(a) = b
설명	위 부등식은 f(x) = x^(p-1)과 g(y) = y^(q-1)을 사용하여 유도할 수 있으며, 여기서 p > 1이고 1/p + 1/q = 1이다.
활용
횔더 부등식 증명	횔더 부등식 증명에 사용됨.
Lp 공간	Lp 공간의 성질 증명에 활용됨.
같이 보기
관련 부등식	횔더 부등식 민코프스키 부등식

2. 초등적 형태

''a''와 ''b''를 음이 아닌 실수라 하고, ''p'', ''q''는 $\frac{1}{p} + \frac{1}{q} = 1$ 을 만족하는 양의 실수라 하자. 그러면 다음 부등식이 성립한다.^[13]

: $ab \le \frac{a^p}{p} + \frac{b^q}{q}.$

이 부등식은 횔더 부등식을 증명하는 데 이용된다. 등호는 $a^p = b^q$ 일 때 성립한다. 이 형태의 영의 부등식은 젠센 부등식으로 증명할 수 있다.

특별히 ''p'' = ''q'' = 2 인 경우, 다음 부등식이 성립한다.

: $ab \le \frac{a^2}{2} + \frac{b^2}{2}$

이 부등식은 더 초등적인 방법으로 증명할 수 있다. 또한, 임의의 양수 ε에 대해 다음 부등식도 성립한다.

: $ab \le \frac{a^2}{2\varepsilon} + \frac{\varepsilon b^2}{2}$

2. 1. 증명 (로그 함수의 오목성 이용)

로그함수가 오목함수라는 성질과 젠센 부등식을 이용하면 다음을 얻는다.

:

\ln\left(\frac{1}{p}a^p + \frac{1}{q}b^q\right) \ge \frac{1}{p}\ln{a^p} + \frac{1}{q}\ln{b^q} = \ln(ab).

, 가 음이 아닌실수이고, 이상의 실수 , 가 을 만족할 때(횔더의 의미에서 "켤레 지수"), 다음 부등식이 성립한다.

:

ab \le \frac{a^p}{p} + \frac{b^q}{q}

위 부등식에서 등호가 성립하기 위한 필요충분조건은 이다.

및 로 두면, 로그 함수는 볼록 함수이므로,

:

\ln(t a^p + (1-t) b^q) \ge t \ln(a^p) + (1-t) \ln(b^q) =\ln(a) +\ln(b) = \ln(ab)

가 성립하고, 등호는 일 때에 한하여 성립한다. 양변의 멱을 취하면 원하는 결과를 얻는다.

2. 2. 일반화 (n개의 변수)

n개의 양수

a_1, ..., a_n

가

\sum_{i=1}^n a_i = 1

을 만족할 때, n개의 음이 아닌 실수

t_1, ..., t_n

에 대하여 다음 부등식이 성립한다.^[14] 일반화한 이 형태 역시 옌센 부등식에 의해 얻을 수 있다.

$\prod_{i=1}^n t_i^{a_i} \le \sum_{i=1}^n a_it_i.$

2. 3. 역함수의 적분 형태

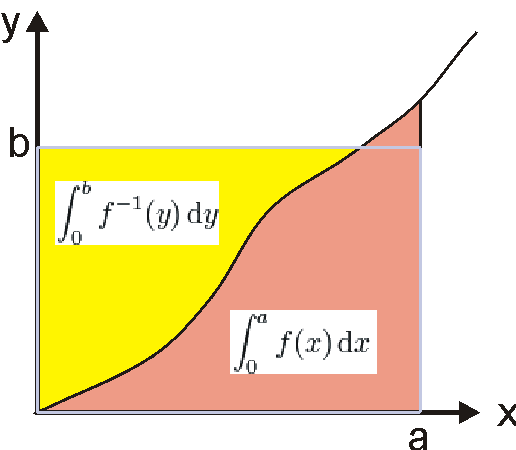
a, b로 만들어지는 직사각형 영역의 면적은 f 아래의 면적(빨간색)과 ''f''⁻¹ 아래의 면적(노란색)의 합을 넘지 않는다.

[0, c]에서 실수로 가는 연속 함수이고 f(0) = 0인 강증가함수 f의 역함수를

f^{-1}

이라 하면, 다음 부등식이 성립한다.^[11]^[12]

:

ab \le \int_0^a f(x)\,dx + \int_0^b f^{-1}(x)\,dx.

여기서

a \in [0, c]

이고

b \in [0, f(c)]

이다. 등호가 성립하기 위한 필요충분조건은

b = f(a)

이다.

3. 표준 형태 (켤레 횔더 지수)

''a''와 ''b''를 음이 아닌 실수로, ''p''와 ''q''를 $\frac{1}{p} + \frac{1}{q} = 1$ 을 만족하는 양의 실수라고 할 때, 다음 부등식이 성립한다.^[13]

: $ab \le \frac{a^p}{p} + \frac{b^q}{q}.$

이 부등식은 횔더 부등식을 증명하는 데 사용되며, 등호는 $a^p = b^q$ 일 때 성립한다.

영의 부등식은 젠센 부등식으로 증명할 수 있다.

3. 1. 증명 (기하학적 접근)

\tfrac{1}{p} + \tfrac{1}{q} = 1

이므로,

p - 1 = \tfrac{1}{q-1}

이다.

x y

평면에서 그래프

y = x^{p-1}

은 따라서 그래프

x = y^{q-1}

이기도 하다. 이 곡선과 축 사이의 면적과,

x=0, x=a, y=0, y=b,

및

y

가 증가하는

x

에 대해 항상 증가하고 그 반대도 마찬가지라는 사실에 의해 경계가 정해지는 직사각형의 면적을 시각적으로 표현하면,

\int^a_0 x^{p-1} \mathrm{d}x

는 곡선 아래 직사각형의 면적을 상한으로 하고(

b\ge a^{p-1}

일 때 등호 성립),

\int^b_0 y^{q-1} \mathrm{d}y

는 곡선 위의 직사각형의 면적을 상한으로 한다(

b\le a^{p-1}

일 때 등호 성립). 따라서

\int^a_0 x^{p-1} \mathrm{d}x + \int^b_0 y^{q-1} \mathrm{d}y \geq ab,

이며

b=a^{p-1}

(또는 동등하게

a^p=b^q

)일 때 등호가 성립한다. 영 부등식은 적분을 평가하여 얻을 수 있다.^[2]

3. 2. 증명 (젠센 부등식 이용)

로그 함수는 오목하므로, 젠센 부등식을 적용하면 다음을 얻는다.^[2]

:

\ln\left(t a^p + (1-t) b^q\right) ~\geq~ t \ln\left(a^p\right) + (1-t) \ln\left(b^q\right) = \ln(a) + \ln(b) = \ln(ab)

여기서

t = 1/p

이고

(1 - t) = 1/q

이다. 등호는

a^p = b^q

일 때만 성립한다. 양변에 지수를 취하면 영 부등식을 얻을 수 있다.

3. 3. 다른 증명 (볼록성 논증)

로그 함수가 오목하다는 성질을 이용하여 영의 부등식을 증명할 수 있다.

a > 0

과

b > 0

에 대해,

t = 1/p

와

(1 - t) = 1/q

를 설정하면 다음과 같은 부등식이 성립한다.^[2]

:

\ln\left(t a^p + (1-t) b^q\right) ~\geq~ t \ln\left(a^p\right) + (1-t) \ln\left(b^q\right) = \ln(a) + \ln(b) = \ln(ab)

여기서 등호는

a^p = b^q

일 때에만 성립한다. 양변에 지수를 취하면 영의 부등식을 얻을 수 있다.

또 다른 증명 방법으로는, 먼저

b = 1

인 경우를 증명하고, 그 결과를

\tfrac{a}{b^q}

에 적용하는 방식이 있다. 이 증명은 횔더 켤레 지수가 영 부등식을 만족시키는 유일한 매개변수임을 보여준다.

0 <\alpha<1

이고

\alpha + \beta = 1

일 때, 다음 부등식은 오직

\alpha = \tfrac{1}{p}

일 때만 성립한다.

:

x ~\leq~ \alpha x^p + \beta, \qquad\, for \quad\ all \quad\ x ~\geq~ 0

이는 볼록성 논증이나 단일 변수 함수의 최소화를 통해 증명할 수 있다.

a > 0

과

b > 0

일 때, 위 부등식에

x=\tfrac{a}{b^s}

를 대입하면 다음을 얻는다.

:

\tfrac{a}{b^s} ~\leq~ \tfrac{1}{p}\tfrac{a^p}{b^{sp}} + \tfrac{1}{q}.

s = q-1

을 선택하고 양변에

b^{q+1}

을 곱하면 영 부등식이 유도된다.

3. 4. 가중 산술-기하 평균 부등식과의 관계

로그 함수는 오목 함수이므로, 영 부등식은 가중 산술·기하 평균 부등식과 동등한 형태로 쓸 수 있다.^[2]

:

a^\alpha b^\beta \leq \alpha a + \beta b, \qquad\, 0 \leq \alpha, \beta \leq 1, \quad\ \alpha + \beta = 1.

등호는

a = b

이거나

\{\alpha, \beta\} = \{0, 1\}.

일 때만 성립한다.

4. 일반화 (Generalizations)

영의 부등식은 여러 변수로 일반화될 수 있다.

만약 $0 \leq p_i \leq 1$ 이고 $\sum_i p_i = 1$ 이면, 다음 부등식이 성립한다.

: $\prod_i {a_i}^{p_i} ~\leq~ \sum_i p_i a_i.$

등호는 영이 아닌 $p_i$ 를 갖는 모든 $a_i$ 가 같을 때 성립한다. 이 부등식은 횔더 부등식을 증명하는데 사용될 수 있다.

4. 1. 최소화 형태

Jensen's inequality|옌센 부등식^영어은 최솟값 형태로 일반화될 수 있다.

만약

a > 0

및

b > 0

이고,

1 < p < \infty

이며

q

가

\tfrac{1}{p} + \tfrac{1}{q} = 1

을 만족한다면, 다음 식이 성립한다.

a b ~=~ \min_{0 < t < \infty} \left(\frac{t^p a^p}{p} + \frac{t^{-q} b^q}{q}\right).

t := 1

을 사용하고

a

를

a^{1/p}

로,

b

를

b^{1/q}

로 대체하면 다음 부등식이 성립한다.

a^{1/p} \, b^{1/q} ~\leq~ \frac{a}{p} + \frac{b}{q},

이 부등식은 횔더 부등식을 증명하는 데 유용하다.

만약

0 \leq p_i \leq 1

이고

\sum_i p_i = 1

이면, 다음이 성립한다.

\prod_i {a_i}^{p_i} ~\leq~ \sum_i p_i a_i.

등호는 영이 아닌

p_i

를 갖는 모든

a_i

가 같을 때 성립한다.

4. 2. n개 변수에 대한 일반화

n개의 양수

a_1, ..., a_n

가

\sum_{i=1}^n a_i = 1

을 만족할 때, n개의 음이 아닌 실수

t_1, ..., t_n

에 대하여 다음 부등식이 성립한다.^[14]

:

\prod_{i=1}^n t_i^{a_i} \le \sum_{i=1}^n a_it_i.

이 일반화된 형태 역시 옌센 부등식에 의해 얻을 수 있다.

만약

0 \leq p_i \leq 1

이고

\sum_i p_i = 1

이면, 다음 부등식이 성립한다.

:

\prod_i {a_i}^{p_i} ~\leq~ \sum_i p_i a_i.

등호는 영이 아닌

p_i

를 갖는 모든

a_i

가 같을 때 성립한다.

5. 초등적 형태 (지수 2)

음이 아닌 실수 a와 b에 대해, 지수가 2인 경우의 영의 부등식은 다음과 같이 나타낼 수 있다.

: $ab \le \frac{a^2}{2} + \frac{b^2}{2}$

이는 옌센 부등식의 특수한 경우(p = q = 2)이지만, 더 기본적인 증명이 가능하다.

모든 실수의 제곱은 0 또는 양수이므로, 임의의 실수 쌍 a와 b에 대해 다음이 성립한다.

: $0 \leq (a-b)^2$

우변을 전개하면 다음과 같다.

: $0 \leq a^2 - 2 a b + b^2$

양변에 2ab를 더하고, 2로 나누면 지수가 2인 경우의 영의 부등식을 얻는다.

: $2 a b \leq a^2 + b^2$

: $a b \leq \frac{a^2}{2} + \frac{b^2}{2}$

5. 1. ε에 대한 옌센 부등식 (Peter-Paul inequality)

지수 2를 가진 영의 부등식은 다음과 같다.^[3]

:

a b \leq \frac{a^2}{2} + \frac{b^2}{2}

이는

\varepsilon

에 대한 영의 부등식(모든

\varepsilon > 0

에 유효)으로, 다음과 같이 나타낼 수 있다.^[3]

:

a b ~\leq~ \frac{a^2}{2 \varepsilon} + \frac{\varepsilon b^2}{2}.

이는 "피터-파울 부등식"이라고도 불리는데, 두 번째 항에 대한 더 엄격한 제어가 첫 번째 항에 대한 일부 제어를 잃는 대가로 이루어진다는 사실을 나타낸다. 즉, "피터에게서 빼앗아 파울에게 지불해야" 한다.^[3]

\varepsilon

에 대한 영의 부등식은 지수 2를 갖는 영의 부등식에

a' = a/\sqrt{\varepsilon}, \; b' = \sqrt{\varepsilon} b

를 대입하여 얻을 수 있다.

6. 행렬 형태 (Matricial generalization)

안도 쓰요시(Tsuyoshi Ando)는 뢰브너 순서에 의해 정렬된 복소 행렬에 대한 영의 부등식의 일반화를 증명했다.^[4] 이는 $n$ 차 정방 행렬 $A, B$ 의 임의의 쌍에 대해 다음을 만족하는 유니타리 행렬 $U$ 가 존재한다는 것을 의미한다.

: $U^* |A B^*| U \preceq \tfrac{1}{p} |A|^p + \tfrac{1}{q} |B|^q,$

여기서 ${}^*$ 는 행렬의 켤레 전치 행렬을 나타내고 $|A| = \sqrt{A^* A}.$ 이다.^[4]^[10]

안도 타케시는 복소 행렬에 대한 영의 부등식의 일반화(순서는 Loewner order|뢰브너 순서^영어에 따른다)를 제시했다.

; 정리 (행렬 영 부등식): 차수 $n$ 의 임의의 복소 행렬 쌍 $A, B$ 에 대해, 유니타리 행렬 $U$ 가 유일하게 존재하여 $U^{*} |AB^{*}| U \preceq \frac{1}{p}|A|^{p} + \frac{1}{q} |B|^{q}$ 와 같이 만들 수 있다. 여기서 *는 행렬의 수반이며, $|A| := \sqrt{A^{*}A}$ 이다.

7. 증가 함수를 이용한 일반화 (Standard version for increasing functions)

0, c에서 실수값을 가지는 연속 함수이고 f(0) = 0인 강증가함수 f에 대해 f의 역함수를 $f^{-1}$ 이라 하면, 다음 부등식이 성립한다.^[5]^[6]

: $ab \le \int_0^a f(x)\,dx + \int_0^b f^{-1}(x)\,dx.$

여기서 $a \in [0, c]$ 이고 $b \in [0, f(c)]$ 이다.

$f(x) = x^{p-1}$ 와 $f^{-1}(y) = y^{q-1}$ 를 적용하면, 이 식은 켤레 횔더 지수에 대한 표준 버전으로 축소된다.

임의의 $a \in [0, c]$ 및 $b \in [0, f(c)]$ 에 대해,

: $ab \le \int_0^a f(x)\,dx + \int_0^b f^{-1}(x)\,dx$ 이고, 등호는 $b = f(a)$ 일 때 성립한다.^[11]^[12]

8. 펜켈-르장드르 변환을 이용한 일반화 (Generalization using Fenchel–Legendre transforms)

실수 함수 $f$ 의 볼록 공액 함수를 $g$ 로 나타내면, 다음 부등식을 얻을 수 있다.

: $a b ~\leq~ f(a) + g(b).$

이는 볼록 공액 함수의 정의로부터 바로 유도된다. 볼록 함수 $f$ 의 경우, 이는 또한 르장드르 변환으로부터도 유도된다.

더 일반적으로, $f$ 가 실수 벡터 공간 $X$ 에서 정의되고 그 볼록 공액 함수가 $f^\star$ 로 표시되는 경우(그리고 쌍대 공간 $X^\star$ 에서 정의되는 경우), 다음이 성립한다.

: $\langle u, v \rangle \leq f^\star(u) + f(v).$

여기서 $\langle \cdot , \cdot \rangle : X^\star \times X \to \Reals$ 는 쌍대 쌍이다.

이 내용은 르장드르 변환의 정의에서 바로 유도된다.

8. 1. 예시 (Examples)

의 르장드르 변환은 이다. 여기서 이므로, 처음에 언급한 횔더 공액 지수에 대한 영의 부등식은 특별한 경우이다.

의 르장드르 변환은 이므로, 가 임의의 에 대해 성립한다. 이 평가식은 지수 모멘트 조건 하의 대편차 이론에서 유용하다. 그 이유는 가 사노프 정리의 율 함수인 상대 엔트로피에 나타나기 때문이다.

9. 합성곱 형태 (Convolution)

Minkowski^영어 적분부등식을 이용하면 합성곱에 대한 옌센 부등식을 유도할 수 있다.^[15]

: $1 \le p, q, r \le \infty$ 이고 $\frac{1}{p} + \frac{1}{q} = \frac{1}{r} + 1$ 일 때, $f \in L^p, g \in L^q$ 이면 $f*g \in L^r$ 이고, 다음 부등식이 성립한다.

:: $||f*g||_r \le ||f||_p||g||_q.$

참조

_[1] 논문 On classes of summable functions and their Fourier series
_[2] 웹사이트 Math 209D - Real Analysis Summer Preparatory Seminar Lecture Notes https://pi.math.corn[...] 2022-09-17
_[3] Youtube The Peter Paul Inequality https://www.youtube.[...] YouTube video on Dr Chris Tisdell's YouTube channel
_[4] 서적 Operator Theory in Function Spaces and Banach Lattices Springer 1995
_[5] 서적 Inequalities http://www.cambridge[...] Cambridge University Press
_[6] 서적 Lectures on the Theory of Integration https://archive.org/[...] World Scientific
_[7] 논문 An extension of Young's inequality Hindawi 2011
_[8] 논문 On classes of summable functions and their Fourier series
_[9] Youtube The Peter Paul Inequality https://www.youtube.[...] YouTube video on Dr Chris Tisdell's YouTube channel
_[10] 서적 Operator Theory in Function Spaces and Banach Lattices Springer 1995
_[11] 서적 Inequalities http://www.cambridge[...] Cambridge University Press
_[12] 서적 Lectures on the Theory of Integration World Scientific
_[13] 서적 실해석 서울대학교출판부 2002
_[14] 서적 같은 책
_[15] 서적 실해석 & 함수해석학 교우사 2002

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com