운동학
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
운동학은 물체의 움직임을 연구하는 학문으로, 어원은 고대 그리스어 '키네마'(운동)에서 유래했다. 입자의 위치, 속도, 가속도를 시간의 함수로 나타내며, 상대 운동 개념을 통해 두 물체의 상대적인 움직임을 분석한다. 운동학은 직교 좌표계, 원통 좌표계 등 다양한 좌표계를 사용하여 물체의 움직임을 설명하며, 병진 운동, 회전 운동, 평면 운동과 같은 운동의 종류를 다룬다. 또한, 기계 시스템의 구성 요소 움직임에 대한 제약을 나타내는 운동 제약과 강체가 연결된 운동 사슬 개념을 통해 기구 및 로봇의 움직임을 분석한다. 운동학은 기계 시스템, 로봇 공학, 생체 역학 등 다양한 분야에 응용된다.
더 읽어볼만한 페이지
- 운동학 - 4절 링크
4절 링크는 4개의 링크가 4개의 1자유도 관절로 연결된 기구로, 관절 조합에 따라 다양한 유형이 존재하며, 각 링크는 특정 역할을 수행하고, 그라쇼프 조건은 움직임 특성을 예측하는 데 사용되며, 여러 기계 시스템에 활용되는 기계 공학의 중요한 연구 분야이다. - 운동학 - 가상일
가상일은 역학계에서 외력이 가상 변위에 대해 하는 일의 합으로, 정역학에서는 계의 정적 평형 조건으로 활용되며, 달랑베르 원리를 통해 동역학에도 적용되어 구조 해석 및 계산에 널리 쓰이는 물리량이다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 표시 이름과 문서 제목이 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다. - 한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 라우토카
라우토카는 피지 비치레부섬 서부에 위치한 피지에서 두 번째로 큰 도시이자 서부 지방의 행정 중심지로, 사탕수수 산업이 발달하여 "설탕 도시"로 알려져 있으며, 인도에서 온 계약 노동자들의 거주와 미 해군 기지 건설의 역사를 가지고 있고, 피지 산업 생산의 상당 부분을 담당하는 주요 기관들이 위치해 있다. - 한국어 위키백과의 링크가 위키데이터와 같은 위키공용분류 - 코코넛
코코넛은 코코넛 야자나무의 열매로 식용 및 유지로 사용되며, 조리되지 않은 과육은 100g당 354kcal의 열량을 내는 다양한 영양 성분으로 구성되어 있고, 코코넛 파우더의 식이섬유는 대부분 불용성 식이섬유인 셀룰로오스이며, 태국 일부 지역에서는 코코넛 수확에 훈련된 원숭이를 이용하는 동물 학대 문제가 있다.
| 운동학 | |
|---|---|
| 지도 정보 | |
| 운동학 | |
| 설명 | 힘을 고려하지 않고 물체의 운동을 기술하는 물리학의 한 분야 |
| 분야 | 고전역학 |
| 주요 개념 | 변위 속도 가속도 |
| 참고 문헌 | |
| 도서 | Whittaker, E. T. (1904). 입자 및 강체의 해석적 역학에 관한 논문. Cambridge University Press. Beggs, Joseph Stiles (1983). 운동학. Taylor & Francis. Wright, Thomas Wallace (1896). 운동학, 동역학 및 정역학을 포함한 역학의 요소. E and FN Spon. Hibbeler, Russell C. (2009). 공학 역학: 동역학. Prentice Hall. Shabana, Ahmed A. (2003). 다체 시스템의 역학. Cambridge University Press. Teodorescu, P. P. (2007). 기계 시스템, 고전 모델: 입자 역학. Springer. Biewener, A. (2003). 동물 운동. Oxford University Press. |
| 운동학 | |
| 설명 | 물체의 운동을 다루는 물리학의 한 분야이며, 운동의 원인인 힘은 고려하지 않는다. |
| 분야 | 고전역학 |
| 주요 개념 | 변위 속도 가속도 |
2. 어원
'운동학'이라는 용어는 A.M. 앙페르가 사용한 ''cinématique''의 영어 번역이다.[9] 앙페르는 그리스어 κίνημα|키네마grc(''운동, 움직임'')에서 이 단어를 만들었는데, 이 단어는 κινεῖν|키네인grc(''움직이다'')에서 파생되었다.[10][11]
운동학(kinematic)과 시네마티크(cinématique)는 프랑스어 단어 시네마(cinéma)와 어근을 공유한다.[12] 시네마는 '움직이는 그림 투영기와 카메라'를 뜻하는 시네마토그래프(cinématographe)의 축약형으로, 그리스어 '운동'과 γρᾰ́φω|grapho|쓰다grc라는 단어에서 유래했다.[12]
2. 1. 운동학 용어의 기원
'운동학'이라는 용어는 A.M. 앙페르가 사용한 ''cinématique''의 영어 번역이다.[9] 앙페르는 그리스어 κίνημα|키네마grc(''운동, 움직임'')에서 이 단어를 만들었는데, 이 단어는 κινεῖν|키네인grc(''움직이다'')에서 파생되었다.[10][11]2. 2. 영화와의 연관성
운동학(kinematic)과 시네마티크(cinématique)는 프랑스어 단어 시네마(cinéma)와 어근을 공유한다.[12] 시네마는 '움직이는 그림 투영기와 카메라'를 뜻하는 시네마토그래프(cinématographe)의 축약형으로, 그리스어 '운동'과 γρᾰ́φω|grapho|쓰다grc라는 단어에서 유래했다.[12]3. 기본 개념
극좌표계에서의 운동학적 벡터. 설정은 2차원 공간에 국한되지 않고, 더 높은 차원의 평면에도 적용됨을 유의하라.
입자 운동학은 입자의 궤적을 연구하는 학문이다. 입자의 위치는 좌표계의 원점에서 입자까지의 좌표 벡터로 정의된다. 예를 들어, 집에서 남쪽으로 50m 떨어진 탑을 생각해 보자. 좌표계가 집 중앙에 있고, 동쪽이 ''x''축 방향이고 북쪽이 ''y''축 방향이라면, 탑 기저부까지의 좌표 벡터는 '''r''' = (0 m, −50 m, 0 m)이다. 탑이 50m 높이이고 이 높이가 ''z''축을 따라 측정된다면, 탑 꼭대기까지의 좌표 벡터는 '''r''' = (0 m, −50 m, 50 m)이다.
가장 일반적인 경우, 입자의 위치를 정의하기 위해 3차원 좌표계가 사용된다. 그러나 입자가 평면 내에서 움직이도록 제한되는 경우 2차원 좌표계로 충분하다. 물리학에서 모든 관측은 참조 좌표계에 대해 설명되지 않고서는 불완전하다.
입자의 ''궤적''은 시간의 벡터 함수인 로, 움직이는 입자가 그리는 곡선을 정의하며 다음과 같이 주어진다.
여기서 , , 그리고 는 시간의 함수로서 입자 위치의 각 좌표를 기술한다.
상대 위치 벡터는 한 점의 위치를 다른 점에 대한 상대적인 위치로 정의하는 벡터이다. 두 점의 위치 차이를 나타낸다. 한 점 A의 다른 점 B에 대한 위치는 단순히 두 점의 위치 차이이다.
:
이는 두 점의 위치 벡터 성분의 차이이다. 점 A의 위치 성분이 이고 점 B의 위치 성분이 이라면, 점 A의 점 B에 대한 위치는 그 성분들의 차이이다:
3. 1. 위치, 속도, 가속도
운동학에서는 물체의 위치, 속도, 가속도를 시간에 대한 함수로 나타낸다.- '''위치''': 좌표계의 원점에서 물체까지의 벡터로 정의되며, 크기와 방향을 갖는다. 3차원에서 위치 벡터 는 다음과 같이 표현될 수 있다.
:
:여기서 , , 는 직교 좌표이고 , , 는 각각 , , 좌표축을 따라있는 단위 벡터이다. 위치 벡터 의 크기는 점 와 원점 사이의 거리를 나타낸다.
:
:위치 벡터의 방향 코사인은 방향의 정량적 척도를 제공한다. 일반적으로, 물체의 위치 벡터는 참조 좌표계에 따라 달라진다. 다른 좌표계는 위치 벡터에 대한 다른 값을 이끌어낸다.
- '''속도''': 위치 벡터의 시간에 대한 변화율로, 물체의 운동 방향과 빠르기를 나타낸다. 시간 간격 동안의 평균 속도는 다음과 같이 정의된다.
:
:여기서 은 시간 간격 동안의 변위 벡터이다. 시간 간격 가 0에 접근하는 극한에서 평균 속도는 위치 벡터의 시간 미분으로 정의되는 순간 속도에 접근한다.
:
:속력은 물체의 속도의 크기이며, 스칼라량이다.
:
:여기서 는 입자의 궤적을 따라 측정된 호의 길이이다.
- '''가속도''': 속도 벡터의 시간에 대한 변화율로, 속도의 크기나 방향의 변화를 나타낸다. 시간 간격에 대한 입자의 평균 가속도는 다음 비율로 정의된다.
:
:여기서 Δ'''v'''는 평균 속도이고 Δ''t''는 시간 간격이다.
:입자의 가속도는 시간 간격이 0에 접근함에 따라 평균 가속도의 극한값이며, 이는 시간 미분이다.
:
:또는,
:
:따라서 가속도는 그 입자의 속도 벡터의 1차 미분과 위치 벡터의 2차 미분이다.
:물체의 가속도의 크기는 가속도 벡터의 크기 |'''a'''|이다. 이것은 스칼라량이다.
:
3. 2. 상대 운동

한 점의 다른 점에 대한 속도는 단순히 두 점의 속도 차이이다.
:
이는 각 속도의 성분 간 차이이다.
점 A의 속도 성분이 이고 점 B의 속도 성분이 이라면, 점 B에 대한 점 A의 속도는 각 성분의 차이이다.
:
또는, 이와 같은 결과는 상대 위치 벡터 '''r'''B/A의 시간 미분을 계산하여 얻을 수 있다.
한 점 C의 다른 점 B에 대한 가속도는 두 점의 가속도 차이와 같다.
:
이는 각 가속도 성분의 차이이다.
점 C의 가속도 성분이 이고 점 B의 가속도 성분이 이면, 점 C의 점 B에 대한 가속도는 각 성분의 차이이다.
:
또는, 상대 위치 벡터 '''r'''B/A의 이계 시간 미분을 계산하여 동일한 결과를 얻을 수 있다.[13]
4. 좌표계
좌표계는 물체의 위치를 나타내는 방법이다. 3차원 공간에서 물체의 위치를 표현하기 위해 다양한 좌표계가 사용된다.
- 직교 좌표계: x, y, z 축을 사용하여 물체의 위치를 나타내는 좌표계이다.
- 원통 좌표계: ''X''–''Y'' 평면에서 입자의 궤적을 극좌표를 사용하여 표현하는 것이 편리할 때 사용된다.
4. 1. 직교 좌표계
3차원 공간에서 물체의 위치를 나타내기 위해 x, y, z 축을 사용하는 좌표계이다. 가장 일반적인 경우, 입자의 위치를 정의하기 위해 3차원 좌표계가 사용된다. 입자의 위치 벡터는 원점에서 입자까지 그려진 벡터이다. 이는 점과 원점 사이의 거리와 원점으로부터의 방향을 모두 나타낸다. 3차원에서 위치 벡터 '''r'''은 다음과 같이 표현될 수 있다.'''r''' = (x, y, z)
여기서 x, y, z는 직교 좌표이고, x, y, z 좌표축 방향을 나타내는 단위 벡터가 사용된다. 위치 벡터의 크기는 점과 원점 사이의 거리를 나타낸다.
위치 벡터의 방향 코사인은 방향의 정량적 척도를 제공한다. 일반적으로, 물체의 위치 벡터는 참조 좌표계에 따라 달라진다. 다른 좌표계는 위치 벡터에 대한 다른 값을 이끌어낸다.
입자의 ''궤적''은 시간의 벡터 함수인 r(t)로 정의되며, 움직이는 입자가 그리는 곡선을 나타낸다.
4. 2. 원통 좌표계
입자의 궤적 '''r'''(''t'') = (''x''(''t''), ''y''(''t''), ''z''(''t''))는 ''X''–''Y'' 평면에서 극좌표를 사용하여 나타내는 것이 편리할 때가 있다. 이렇게 하면 속도와 가속도를 좀 더 다루기 쉬운 형태로 표현할 수 있다.입자 ''P''의 궤적은 고정된 기준틀 ''F''에서 측정된 좌표 벡터 '''r'''로 정의된다. 입자가 움직이면 좌표 벡터 '''r'''(''t'')는 궤적을 그리는데, 이는 공간상의 곡선으로 다음과 같이 표현된다.
여기서 '''x̂''', '''ŷ''', '''ẑ'''는 각각 ''x'', ''y'', ''z'' 축 방향의 단위 벡터이며, 기준틀 ''F''를 따른다.
입자 ''P''가 반지름 ''r''(''t'') = 상수인 원통 표면에서만 움직인다고 가정하면, 고정된 틀 ''F''의 ''z'' 축을 원통의 축과 일치시킬 수 있다. 그러면 ''x''–''y'' 평면에서 이 축을 중심으로 하는 각도 ''θ''를 사용하여 궤적을 다음과 같이 정의할 수 있다.
여기서 중심으로부터의 일정한 거리는 ''r''로 표시되고, ''θ''(''t'')는 시간의 함수이다.
'''r'''(''t'')에 대한 원통 좌표는 방사형 및 접선 방향 단위 벡터를 도입하여 간단하게 나타낼 수 있다.
그리고 기본 미적분에서 시간 도함수는 다음과 같다.
이 표기법을 사용하면 '''r'''(''t'')는 다음과 같이 표현된다.
일반적으로 궤적 '''r'''(''t'')는 원통형 원통에 있는 것으로 제한되지 않으므로, 반지름 ''R''은 시간에 따라 변하고 원통 극좌표에서 입자의 궤적은 다음과 같이 된다.
여기서 ''r'', ''θ'', ''z''는 시간에 대한 연속적으로 미분 가능한 함수일 수 있으며, 간단하게 표현하기 위해 함수 표기법은 생략되었다. 속도 벡터 '''v'''''P''는 궤적 '''r'''(''t'')의 시간 도함수이며, 다음과 같다.
마찬가지로, 속도 '''v'''''P''의 시간 도함수인 가속도 '''a'''''P''는 다음과 같이 주어진다.
항은 경로의 해당 지점에서 경로의 곡률 중심을 향해 작용하며, 일반적으로 구심 가속도라고 한다. 항은 코리올리 가속도라고 한다.
입자가 원통 표면 위에 놓여 있다면 반지름 ''r''은 일정하고, 속도와 가속도 벡터는 간단해진다. '''v'''P의 속도는 궤적 '''r'''(''t'')의 시간에 대한 도함수이며, 다음과 같다.
원통형 실린더 상의 입자 궤적의 특수한 경우는 z축을 따라 이동이 없는 경우이다.
여기서 r과 z0는 상수이다. 이 경우, 속도 '''v'''''P''는 다음과 같이 주어집니다.
여기서 는 실린더의 z축 주위의 단위 벡터 의 각속도이다.
입자 P의 가속도 '''a'''''P''는 이제 다음과 같이 주어집니다.
다음의 성분
는 각각 가속도의 ''방사분력'' 및 ''접선분력''이라고 한다.
5. 운동의 종류
운동학에서는 물체가 어떤 방식으로 움직이는지 다룬다. 대표적인 운동의 종류는 다음과 같다.
- 병진 운동: 물체가 회전하지 않고 직선이나 곡선 경로를 따라 이동하는 것을 말한다. 이때 물체의 모든 부분은 같은 속도와 가속도로 움직인다.[20]
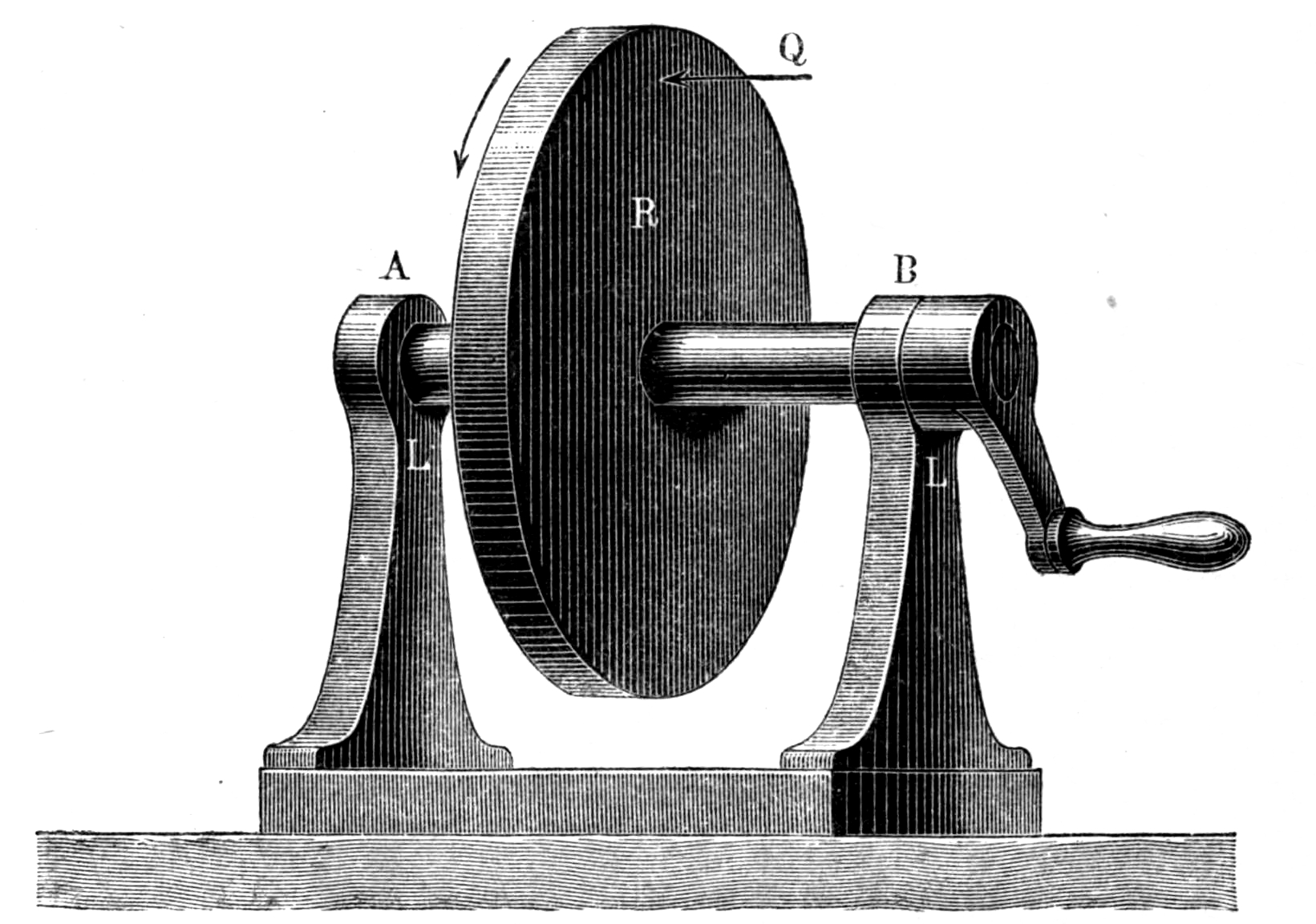
- 회전 운동: 물체가 고정된 축을 중심으로 회전하는 운동이다. 각도, 각속도, 각가속도와 같은 개념을 사용하여 설명할 수 있다.
- 평면 운동: 물체의 모든 점이 평행한 평면 위에서 움직이는 운동이다. 병진 운동과 회전 운동의 조합으로 나타낼 수 있다.[20]
증기 기관의 각 부분이 움직이는 모습은 연속적인 강체 변위의 집합으로 모델링할 수 있다.[20]
5. 1. 병진 운동
물체가 회전 없이 직선 또는 곡선 경로를 따라 이동하는 운동을 병진 운동이라고 한다. 병진 운동에서 물체의 모든 점은 동일한 속도와 가속도를 갖는다.[20]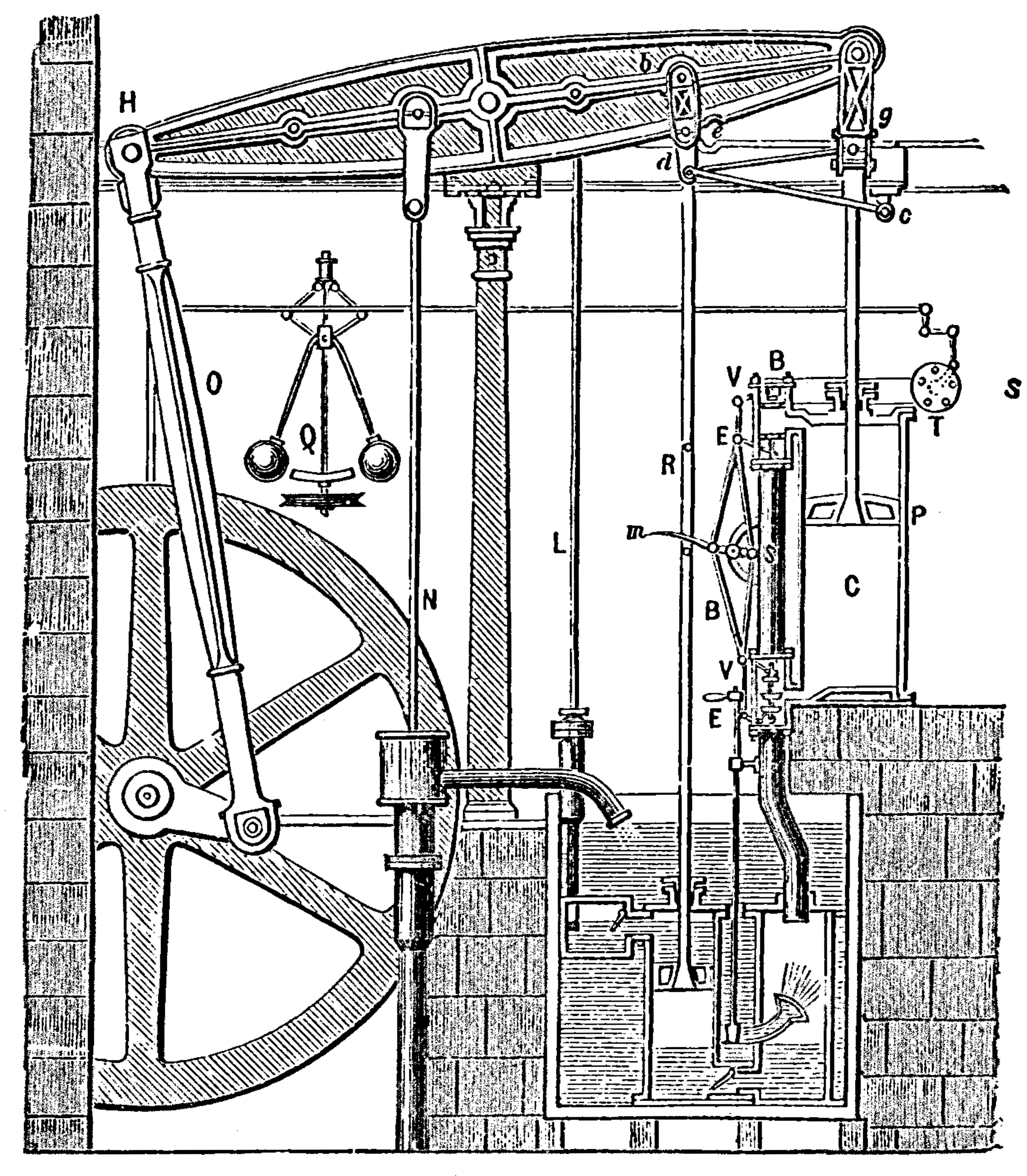
기계 시스템에서 한 구성 요소의 위치를 다른 구성 요소에 대해 나타낼 때는, 한 구성 요소에 고정된 프레임 ''F''에 대해 상대적으로 움직이는 다른 구성 요소에 기준 프레임 ''M''을 도입한다. ''M''의 ''F''에 대한 강체 변환(변위)은 두 구성 요소의 상대적 위치를 정의하는데, 이는 회전과 병진 운동의 조합으로 구성된다.
''M''의 ''F''에 대한 모든 변위의 집합을 ''M''의 위상 공간이라고 한다. 이 위상 공간에서 한 위치에서 다른 위치로 부드럽게 이어지는 곡선은 연속적인 변위 집합이며, ''M''의 ''F''에 대한 운동이다. 즉, 물체의 운동은 연속적인 회전과 병진 운동의 집합으로 구성된다.
평면 '''R'''2에서 회전과 병진의 조합은 동차 변환(homogeneous transform)으로 알려진 특정 유형의 3×3 행렬로 나타낼 수 있다. 이 3×3 동차 변환은 2×2 회전 행렬 ''A''(''φ'')와 2×1 병진 벡터 '''d''' = (''dx'', ''dy'')로부터 다음과 같이 구성된다.
이러한 동차 변환은 평면 ''z'' = 1 (좌표 '''r''' = (''x'', ''y'', 1)을 갖는 점들)에 강체 변환을 수행한다.
'''r'''이 고정된 기준좌표계 ''F''와 일치하는 참조 좌표계 ''M''의 점들의 좌표를 정의한다고 할 때, ''M''의 원점이 ''F''의 원점에 대해 병진 벡터 '''d'''만큼 이동하고 ''F''의 x축에 대해 φ만큼 회전하면, ''M''의 점들의 ''F''에서의 새로운 좌표는 다음과 같이 주어진다.
동차 변환은 아핀 변환을 나타낸다. 병진이 '''R'''2의 선형 변환이 아니기 때문에 이러한 공식화가 필요하다. 그러나 투영 기하학을 사용하여 '''R'''2를 '''R'''3의 부분집합으로 간주하면 병진은 아핀 선형 변환이 된다.[20]
강체가 움직일 때, 그 기준틀 ''M''이 고정된 틀 ''F''에 대해 회전하지 않는다면(''θ'' = 0) 이러한 운동을 순수 병진 운동이라고 한다. 이 경우, 물체 내 모든 점의 궤적은 ''M''의 원점의 궤적 '''d'''(''t'')에 대한 오프셋으로 표현된다.
따라서 순수 병진 운동을 하는 물체의 경우, 물체 내 모든 점 ''P''의 속도와 가속도는 다음과 같이 주어진다.
여기서 점은 시간에 대한 미분을 나타내고, '''v'''''O''와 '''a'''''O''는 각각 움직이는 틀 ''M''의 원점의 속도와 가속도이다. ''M''에서의 좌표 벡터 '''p'''는 상수이므로, 그 미분은 0이다.
5. 2. 회전 운동
물체가 고정된 축을 중심으로 회전하는 운동을 회전 운동이라고 한다. 이 운동은 각도, 각속도, 각가속도 등의 개념을 사용하여 기술할 수 있다.고정축 주위 회전:
z축을 중심으로 회전하는 간단한 회전의 경우, 회전은 평면 기준틀 M이 고정된 기준틀 F에 대해 공유하는 z축을 중심으로 한 각 위치로 설명될 수 있다. M에서의 좌표 '''p''' = (''x'', ''y'')는 F에서의 좌표 '''P''' = (X, Y)와 다음과 같은 행렬 방정식으로 관련된다.
여기서
는 회전 행렬이며, 시간의 함수로서 M의 F에 대한 각 위치를 정의한다.
점 '''p'''가 ''M''에서 움직이지 않는다고 가정하면, ''F''에서의 속도는 다음과 같이 주어진다.
좌표 '''p'''를 제거하고 궤적 '''P'''(''t'')에 대한 연산으로 표현하면,
가 된다. 여기서 행렬
은 ''F''에 대한 ''M''의 각속도 행렬이다. 매개변수 ''ω''는 각도 ''θ''의 시간에 대한 도함수, 즉
이다.
'''P'''(t)의 ''F''에서의 가속도는 속도의 시간 미분으로 얻어진다.
이는 다음과 같이 정리할 수 있다.
여기서
는 ''F''에 대한 ''M''의 각가속도 행렬이고,
이다.
회전 운동은 다음 세 가지 양을 포함하여 설명한다.
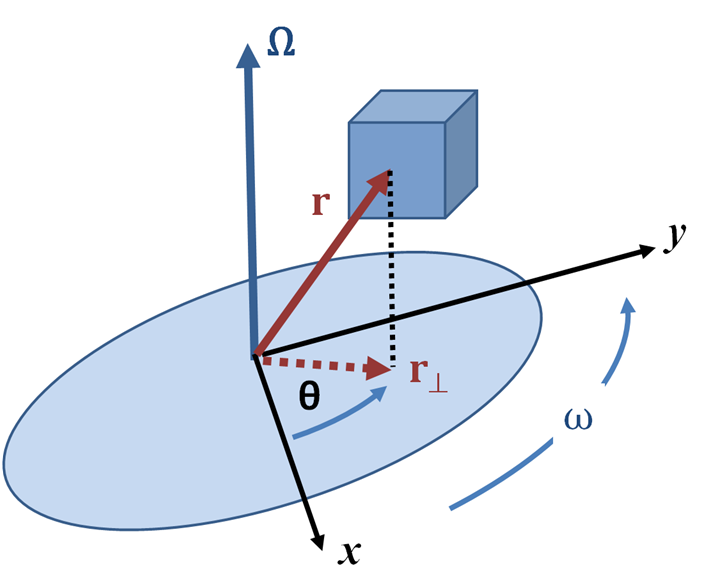
- '''각도(각 위치)''': 회전축 상의 선택된 원점에서 물체의 한 점까지의 방향이 있는 거리는 점의 위치를 나타내는 벡터 '''r'''(t)이다. 벡터 '''r'''(t)는 회전축에 수직인 평면에 투영(또는 동등하게, 어떤 성분) '''r'''⊥(t)를 갖는다. 그러면 그 점의 ''각도(각 위치)''는 기준축(일반적으로 양의 ''x''축)에서 알려진 회전 방향(일반적으로 오른손 법칙에 의해 주어짐)의 벡터 '''r'''⊥(t)까지의 각도 ''θ''이다.
- '''각속도''': 각속도 ''ω''는 각도 ''θ''가 시간 ''t''에 따라 변하는 비율이다:
각속도는
- '''각가속도''': 각가속도 ''α''의 크기는 각속도 ''ω''가 시간 ''t''에 따라 변하는 비율이다:
등각가속도를 갖는 평면 회전 운동학에 대한 병진 운동학 방정식은 간단한 변수 교환으로 쉽게 확장될 수 있다.
여기서 ''θ''i와 ''θ''f는 각각 초기 및 최종 각도(각 위치), ''ω''i와 ''ω''f는 각각 초기 및 최종 각속도, ''α''는 일정한 각가속도이다. 공간에서의 위치와 공간에서의 속도는 모두 각속도와 마찬가지로 (회전에 대한 그들의 성질 측면에서) 참 벡터이지만, 각도 자체는 참 벡터가 아니다.
5. 3. 평면 운동
물체의 모든 점이 평행한 평면에서 움직이는 운동을 평면 운동이라고 한다. 평면 운동은 병진 운동과 회전 운동의 조합으로 나타낼 수 있다.기계 시스템에서 한 구성 요소의 다른 구성 요소에 대한 위치는, 한 구성 요소에 고정된 프레임 ''F''에 대해 상대적으로 움직이는 다른 구성 요소에 기준 프레임 ''M''을 도입하여 정의할 수 있다. ''M''의 ''F''에 대한 강체 변환 또는 변위는 두 구성 요소의 상대적 위치를 정의하는데, 이는 회전과 병진운동의 조합으로 구성된다.[20]
''M''의 ''F''에 대한 모든 변위의 집합을 ''M''의 위상 공간이라고 한다. 이 위상 공간에서 한 위치에서 다른 위치로 부드럽게 이어지는 곡선은 연속적인 변위 집합이며, ''M''의 ''F''에 대한 운동이라고 한다. 물체의 운동은 연속적인 회전과 병진운동의 집합으로 구성된다.[20]
평면 '''R'''2에서의 회전과 병진의 조합은 동차 변환(homogeneous transform)으로 알려진 특정 유형의 3×3 행렬로 나타낼 수 있다. 3×3 동차 변환은 2×2 회전 행렬 ''A''(''φ'')와 2×1 병진 벡터 '''d''' = (''dx'', ''dy'')로부터 다음과 같이 구성된다.[20]
이러한 동차 변환은 평면 ''z'' = 1, 즉 좌표 '''r''' = (''x'', ''y'', 1)을 갖는 점들에 강체 변환을 수행한다.[20]
특히, '''r'''이 고정된 기준좌표계 ''F''와 일치하는 참조 좌표계 ''M''의 점들의 좌표를 정의한다고 할 때, ''M''의 원점이 ''F''의 원점에 대해 병진 벡터 '''d'''만큼 이동하고 ''F''의 x축에 대해 φ만큼 회전할 때, ''M''의 점들의 ''F''에서의 새로운 좌표는 다음과 같이 주어진다.[20]
동차 변환은 아핀 변환을 나타낸다. 병진이 '''R'''2의 선형 변환이 아니기 때문에 이러한 공식화가 필요하다. 그러나 투영 기하학을 사용하여 '''R'''2를 '''R'''3의 부분집합으로 간주하면 병진은 아핀 선형 변환이 된다.[20]
6. 운동 제약
운동 제약은 기계 시스템 구성 요소의 움직임에 대한 제약 조건이다. 운동 제약은 크게 두 가지 형태로 생각할 수 있다. (i) 시스템의 구조를 정의하는 경첩, 슬라이더 및 캠 조인트에서 발생하는 제약 조건으로, 이는 홀로노믹 제약 조건이라고 한다. (ii) 평면 위의 스케이트 날 제약이나 평면과 접촉하는 원반 또는 구의 미끄럼 없이 구르는 것과 같이 시스템의 속도에 부과되는 제약 조건으로, 이는 비홀로노믹 제약 조건이라고 한다.[19]
운동 결합은 6자유도를 모두 정확하게 구속한다.
프란츠 로이올은 기계를 구성하는 부품 간의 이상적인 연결을 운동쌍이라고 불렀다. 그는 두 링크 사이에 선 접촉이 있는 고차 운동쌍과 링크 사이에 면 접촉이 있는 저차 운동쌍으로 구분했다. J. 필립스는 이러한 단순한 분류에 맞지 않는 운동쌍을 구성하는 많은 방법이 있음을 보여준다.[27]
6. 1. 홀로노믹 제약 조건
운동 제약은 기계 시스템 구성 요소의 움직임에 대한 제약 조건이다. 운동 제약은 크게 두 가지 형태로 생각할 수 있는데, (i) 시스템의 구조를 정의하는 경첩, 슬라이더 및 캠 조인트에서 발생하는 제약 조건으로, 이는 홀로노믹 제약 조건이라고 한다. (ii) 시스템의 속도에 부과되는 제약 조건이 있다.[19]프란츠 로이올은 기계를 구성하는 부품 간의 이상적인 연결을 운동쌍이라고 불렀다. 그는 두 링크 사이에 선 접촉이 있는 고차 운동쌍과 링크 사이에 면 접촉이 있는 저차 운동쌍으로 구분했다.[27]
하급쌍은 이상적인 접합 또는 정홀로노믹 구속조건으로, 움직이는 고체(3차원) 내의 점, 선 또는 평면과 고정된 고체 내의 해당 점, 선 또는 평면 사이의 접촉을 유지한다. 다음과 같은 경우가 있다.
- 회전쌍 또는 힌지 접합은 움직이는 물체의 선 또는 축이 고정된 물체의 선과 공선을 유지하고, 이 선에 수직인 움직이는 물체의 평면이 고정된 물체의 유사한 수직 평면과 접촉을 유지해야 한다. 이것은 1자유도를 가지며, 이는 힌지 축을 중심으로 하는 순수 회전이다.
- 프리즘 조인트 또는 슬라이더는 움직이는 물체의 선 또는 축이 고정된 물체의 선과 공선을 유지하고, 이 선에 평행한 움직이는 물체의 평면이 고정된 물체의 유사한 평행 평면과 접촉을 유지해야 한다. 이것은 1자유도를 갖는다. 이 자유도는 선을 따라 슬라이드하는 거리이다.
- 원통형 접합은 움직이는 물체의 선 또는 축이 고정된 물체의 선과 공선을 유지해야 한다. 이 접합은 2자유도를 갖는다. 움직이는 물체의 위치는 축을 중심으로 한 회전과 축을 따라 슬라이드하는 거리 모두에 의해 정의된다.
- 구면 접합 또는 볼 조인트는 움직이는 물체의 점이 고정된 물체의 점과 접촉을 유지해야 한다. 이 접합은 3자유도를 갖는다.
- 평면 접합은 움직이는 물체의 평면이 고정된 물체의 평면과 접촉을 유지해야 한다. 이 접합은 3자유도를 갖는다.
6. 2. 비홀로노믹 제약 조건
시스템의 속도에 부과되는 제약 조건이다. 예를 들어 평면 위의 스케이트 날 제약이나, 평면과 접촉하는 원반 또는 구의 미끄럼 없이 구르는 경우가 이에 해당하며, 비홀로노믹 제약 조건이라고 한다.[22]표면에 미끄러짐 없이 구르는 물체는 질량 중심의 속도가 각속도와 접촉점에서 질량 중심까지의 벡터의 외적과 같다는 조건을 만족한다.
:
넘어지거나 회전하지 않는 물체의 경우, 이는 로 간소화된다.
7. 운동 사슬
프란츠 로이올은 기계를 구성하는 부품 간의 이상적인 연결을 운동쌍이라고 불렀다. 강체("링크")가 운동쌍("조인트")으로 연결된 것을 ''운동 사슬''이라고 한다. 기구와 로봇은 운동 사슬의 예이다. 운동 사슬의 자유도는 이동도 공식을 사용하여 링크의 수와 조인트의 수와 종류로부터 계산된다. 이 공식은 또한 주어진 자유도를 갖는 운동 사슬의 위상을 열거하는 데 사용될 수 있으며, 이는 기계 설계에서 ''형태 합성''으로 알려져 있다.[27]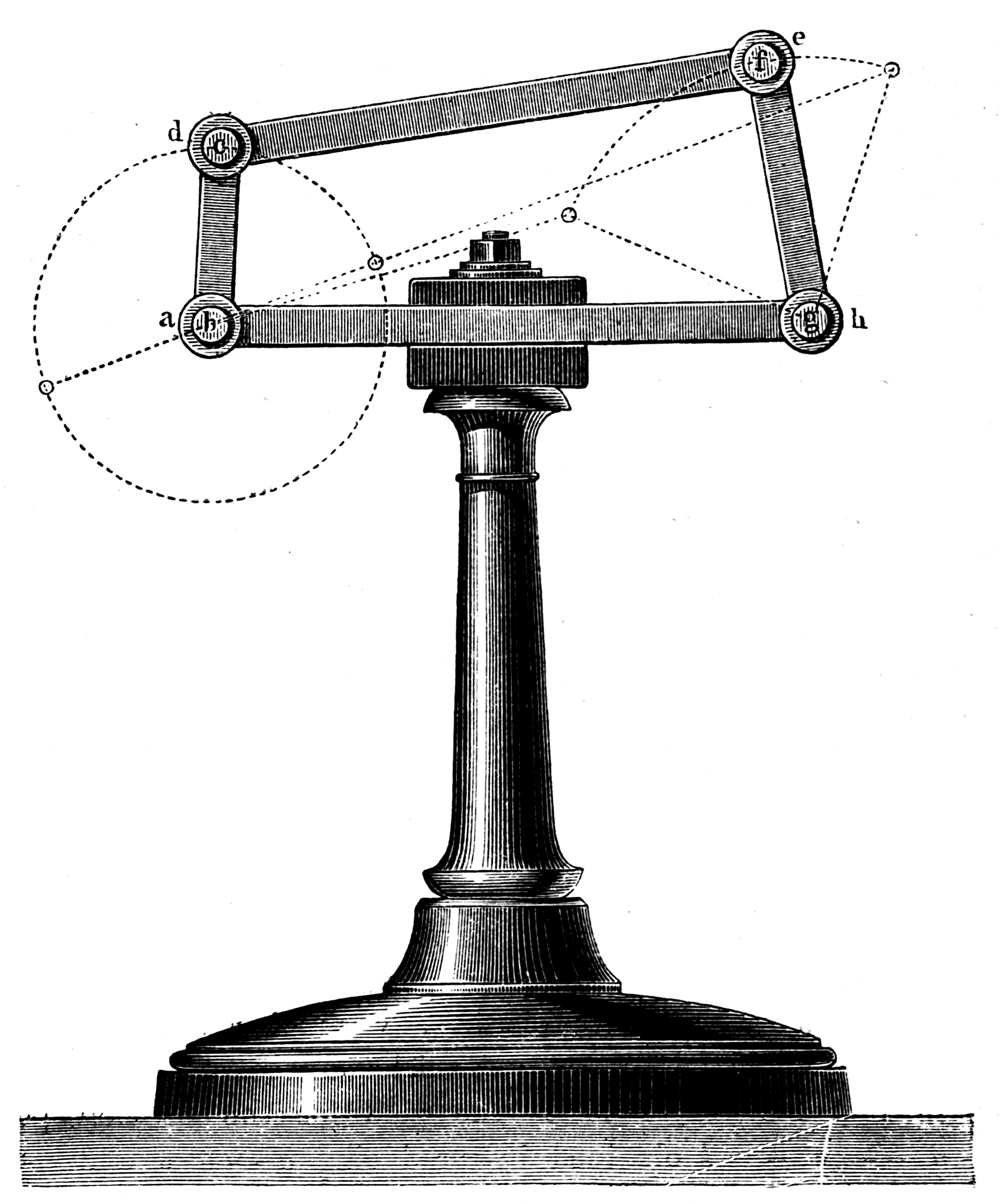
평면 1자유도 기구는 N개의 링크와 j개의 회전 또는 슬라이딩 조인트로 조립되며, 그 예시는 다음과 같다.
8. 응용 분야
운동학은 다음과 같은 다양한 분야에 응용된다.
- 기계 시스템: 기계 시스템의 움직임을 분석하고 설계하는 데 사용된다.
- 로봇 공학: 로봇의 움직임을 계획하고 제어하는 데 활용된다.
- 생체 역학: Biomechanical영어 운동학은 사람이나 동물의 움직임을 분석하고 모델링하는 데 사용된다.
8. 1. 기계 시스템
기계 시스템의 구성 요소 B의 움직임은 동차 변환 [T(t)] = [A(t), d(t)]로 조합된 회전 [A(t)] 및 병진 d(t)의 집합으로 정의된다. 만약 p가 이동하는 기준 좌표계 M에서 측정된 B 내의 점 P의 좌표라면, F에서 추적된 이 점의 궤적은 다음과 같이 주어진다.:\mathbf{P}(t) = [T(t)] \mathbf{p}
::\begin{bmatrix} \mathbf{P} \\ 1\end{bmatrix}
::=\begin{bmatrix} A(t) & \mathbf{d}(t) \\ 0 & 1\end{bmatrix}
::\begin{bmatrix} \mathbf{p} \\ 1\end{bmatrix}.
이 표기법은 P = (X, Y, Z, 1)과 P = (X, Y, Z)를 구분하지 않는다.
P의 궤적에 대한 이 방정식은 M에서 좌표 벡터 p를 계산하기 위해 역으로 계산될 수 있다.
:\mathbf{p} = [T(t)]^{-1}\mathbf{P}(t)
::\begin{bmatrix} \mathbf{p} \\ 1\end{bmatrix}
::=\begin{bmatrix} A(t)^\text{T} & -A(t)^\text{T}\mathbf{d}(t) \\ 0 & 1\end{bmatrix}
::\begin{bmatrix} \mathbf{P}(t) \\ 1\end{bmatrix}.
이 표현식은 회전 행렬의 전치가 그 역행렬이기도 하다는 사실을 사용한다.
:[A(t)]^\text{T}[A(t)]=I.\!
8. 2. 로봇 공학
운동학은 로봇의 움직임을 계획하고 제어하는 데 사용된다. 주어진 소스에는 로봇 공학과 직접 관련된 내용은 없지만, 로봇의 움직임을 기술하는 데 운동학의 속도 및 가속도 공식이 활용될 수 있다는 점을 유추할 수 있다.8. 3. 생체 역학
Biomechanical영어 운동학은 인체나 동물의 움직임을 분석하고 모델링하는 데 사용된다.참조
[1]
서적
A Treatise on the Analytical Dynamics of Particles and Rigid Bodies
Cambridge University Press
[2]
서적
Kinematics
https://books.google[...]
Taylor & Francis
[3]
서적
Elements of Mechanics Including Kinematics, Kinetics and Statics
https://books.google[...]
E and FN Spon
[4]
서적
Engineering Mechanics: Dynamics
Prentice Hall
[5]
서적
Dynamics of Multibody Systems
Cambridge University Press
[6]
서적
Mechanical Systems, Classical Models: Particle Mechanics
Springer
[7]
서적
Animal Locomotion
https://books.google[...]
Oxford University Press
[8]
서적
Geometric Design of Linkages
https://books.google[...]
Springer
[9]
서적
Essai sur la Philosophie des Sciences
https://archive.org/[...]
Chez Bachelier
[10]
서적
A History of European Thought in the Nineteenth Century
https://archive.org/[...]
Blackwood, London
[11]
서적
Theoretical Kinematics
https://books.google[...]
Dover Publications
[12]
문서
cinema
[13]
문서
Crash course physics
[14]
Youtube
2.4 Integration
https://www.youtube.[...]
MIT
2017-06-02
[15]
Youtube
Crash course physics integrals
https://www.youtube.[...]
[16]
웹사이트
Area of Triangles Without Right Angles
https://www.mathsisf[...]
[17]
이미지
kinematics.gif (508×368)
https://www4.uwsp.ed[...]
2023-11-03
[18]
서적
The Kinematics of Machinery: Outlines of a Theory of Machines
https://archive.org/[...]
Macmillan
[19]
웹사이트
Definition of geometry
http://www.merriam-w[...]
Merriam-Webster on-line dictionary
2023-05-31
[20]
서적
Robot manipulators: mathematics, programming, and control : the computer control of robot manipulators
https://books.google[...]
MIT Press, Cambridge, MA
[21]
서적
Chapter 16
https://books.google[...]
Cambridge University
[22]
서적
Elements of Natural Philosophy
https://archive.org/[...]
Cambridge University Press
[23]
서적
Elements of Natural Philosophy
https://books.google[...]
[24]
서적
The Mechanics Problem Solver
Research & Education Association
[25]
서적
Mechanics of Engineering
https://archive.org/[...]
Wiley
[26]
서적
Mathematical Thought from Ancient to Modern Times
https://archive.org/[...]
Oxford University Press
[27]
서적
Freedom in Machinery, Volumes 1–2
https://books.google[...]
Cambridge University Press
[28]
서적
Mechanism design:enumeration of kinematic structures according to function
https://books.google[...]
CRC Press
[29]
웹사이트
한국물리학회 물리학용어집
https://www.kps.or.k[...]
[30]
서적
A Treatise on the Analytical Dynamics of Particles and Rigid Bodies
http://books.google.[...]
Cambridge University Press
[31]
서적
Kinematics
http://books.google.[...]
Taylor & Francis
[32]
서적
Elements of Mechanics Including Kinematics, Kinetics and Statics
http://books.google.[...]
E and FN Spon
[33]
서적
Engineering Mechanics: Dynamics
http://books.google.[...]
Prentice Hall
[34]
서적
Animal Locomotion
http://books.google.[...]
Oxford University Press
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

