유한기하학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 한국 수학과 유한 기하학
3. 유한 평면
4. 3차원 이상의 유한 기하
- 4.1. 유한 3차원 공간
5. 응용
참조

1. 개요

유한 기하학은 유한한 수의 점, 선, 평면 등의 기하학적 구조를 연구하는 수학의 한 분야이다. 유한 기하학은 아핀 기하학과 사영 기하학으로 분류되며, 이 두 종류는 공리 체계에 따라 정의된다. 유한 아핀 평면은 평행선 공준을 만족하며, 유한 사영 평면은 임의의 두 선이 한 점에서 만난다. 유한 평면의 위수는 각 선이 포함하는 점의 개수로 정의되며, 소수 거듭제곱이 유한 평면의 위수가 될 가능성이 높지만, 브루크-라이저 정리는 특정 조건을 만족하는 정수가 유한 평면의 위수가 될 수 없음을 보여준다. 3차원 이상의 유한 기하학은 베블렌-영 정리에 의해 유한체 GF(q)에 대한 n차원 사영 공간 PG(n, q)와 동형이다. 유한 기하학은 조합론, 부호 이론 등 다양한 분야에 응용되며, 커크먼의 여학생 문제와 같은 문제 해결에 활용된다.

더 읽어볼만한 페이지

유한기하학 - 결합 구조
결합 구조는 점과 선의 관계를 통해 정의되는 수학적 구조이며, 부분 결합 구조, 균등 및 정칙 결합 구조 등의 개념을 포함하고, 결합 행렬과 레비 그래프를 통해 시각화 및 분석이 가능하다.
조합론 - 집합의 분할
집합의 분할은 주어진 집합을 서로소인 부분 집합들로 나누는 것이며, 동치 관계와 밀접하게 관련되어 있고, 벨 수로 표현되며, 플레잉 카드를 나누는 것과 같은 예시가 있다.
조합론 - 계승 (수학)
계승은 음이 아닌 정수 n에 대해 1부터 n까지의 자연수를 곱한 값으로, 0의 계승은 1로 정의되며, 대칭군의 크기와 같다는 성질을 통해 기수로 확장될 수 있고, 다중 계승, 지수 계승 등으로 확장 및 응용되어 다양한 분야에서 활용된다.
수학 - 회귀 분석
회귀 분석은 종속 변수와 하나 이상의 독립 변수 간의 관계를 모델링하고 분석하는 통계적 기법으로, 최소 제곱법 개발 이후 골턴의 연구로 '회귀' 용어가 도입되어 다양한 분야에서 예측 및 인과 관계 분석에 활용된다.
수학 - 수학적 최적화
수학적 최적화는 주어진 집합에서 실수 또는 정수 변수를 갖는 함수의 최댓값이나 최솟값을 찾는 문제로, 변수 종류, 제약 조건, 목적 함수 개수에 따라 다양한 분야로 나뉘며 여러 학문 분야에서 활용된다.

유한기하학

2. 역사

유한 기하학에 대한 개별적인 예시는 토마스 페닝턴 키크먼(1847)의 연구와 폰 슈타우트(1856)가 시작한 유한 사영 기하학의 체계적인 발전 과정에서 찾아볼 수 있다.

유한 사영 기하학에 대한 첫 번째 공리적 접근은 이탈리아 수학자 지노 파노에 의해 이루어졌다. 그는 사영 ''n''-공간에 대한 공리들이 서로 독립적임을 보이는 연구 과정에서 유한 개의 점과 선으로 이루어진 기하학적 구조를 탐구하며 유한 기하학 연구의 기초를 다졌다.^[2]^[3]^[4]

1906년에는 오스왈드 베블런과 W. H. 버시가 갈루아체 GF(''q'')의 원소를 이용한 동차 좌표를 사용하여 사영 기하학을 설명했다. 이 접근법에 따라, ''n'' + 1개의 좌표를 사용하는 ''n''차원 유한 기하학은 PG(''n, q'')라는 표기로 나타내게 되었다.^[5] 이러한 유한 기하학은 합성 기하학 분야에서 다루어지며, 관련된 변환 군과 함께 연구된다.

2. 1. 한국 수학과 유한 기하학

유한 기하학은 조합론이나 부호 이론의 여러 문제에 대한 모델을 제공하는 데 활용될 수 있다. 대표적인 예시 중 하나가 커크만의 여학생 문제^[12]이다.

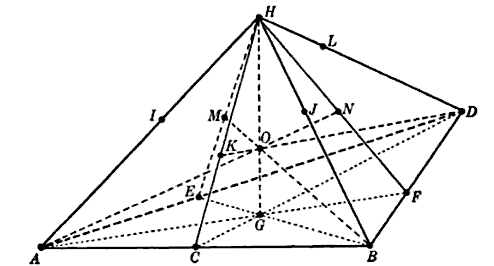
이 문제는 "15명의 여학생이 매일 세 명씩 5개 조로 걷는다. 일주일(7일) 동안 각 조에서 모든 여학생이 단 한 번만 함께 걷도록 시간표를 짜라"는 내용이다. 이 문제의 해답을 구성하는 배경으로 유한 사영 공간인 PG(3,2)가 사용될 수 있다.

PG(3,2)는 유한체 GF(2) 위에서 정의되는 가장 작은 3차원 사영 공간이다. 이 공간은 15개의 점, 35개의 선, 15개의 평면으로 이루어져 있다. 각 평면은 7개의 점과 7개의 선을 포함하며, 파노 평면과 동형이다. 각 선은 3개의 점을 지나고, 모든 점은 7개의 선 위에 있다. 서로 다른 두 점은 정확히 하나의 선을 결정하며, 서로 다른 두 평면은 정확히 하나의 선에서 만난다. 이러한 유한 기하학은 1892년 지노 파노(Gino Fano)가 처음 연구했다.

커크만의 여학생 문제에서, 15명의 여학생은 PG(3,2)의 15개 점에 대응시킬 수 있다. 여학생들이 함께 걷는 3명 조합은 총 35가지인데, 이는 PG(3,2)의 35개 선(각 선은 3개의 점을 포함)에 해당한다. 문제의 해답은 PG(3,2)의 '패킹(packing)' 구조를 이용하여 찾을 수 있다. 먼저 '스프레드(spread)'는 사영 공간의 점들을 서로 만나지 않는 직선들로 나누는 것을 의미한다. PG(3,2)에서 스프레드는 15개의 점을 5개의 서로 만나지 않는 직선(각 직선은 3개의 점, 즉 3명의 여학생을 포함)으로 나누는 것이며, 이는 특정 날짜의 조 편성에 해당한다. '패킹'은 이러한 스프레드들을 서로 겹치지 않게 모은 것으로, PG(3,2)의 패킹은 7개의 서로 다른 스프레드로 구성된다. 이는 일주일 동안의 전체 조 편성을 나타낸다. 커크만의 여학생 문제에는 동형이 아닌 7가지 해답이 있는데, 그중 2가지가 PG(3,2)의 패킹 구조로 표현될 수 있다.

이처럼 유한 기하학, 특히 유한 사영 공간은 특정 조합론적 문제의 구조를 이해하고 해를 구하는 데 유용한 도구가 된다. 유한 기하학은 유한체 위의 벡터 공간 구조와 관련되어 선형대수학을 통해 정의되기도 하며(이를 갈루아 기하라고도 한다), 순수하게 조합론적으로 정의될 수도 있다. 대부분의 경우 이 두 정의는 동일한 구조를 나타내지만, 2차원 사영 평면 중에는 조합론적으로만 정의되고 유한체 위의 사영 공간과는 동형이 아닌 비 데자르그 평면도 존재한다.

3. 유한 평면

유한 평면은 유한한 수의 점과 선으로 이루어진 2차원 기하학 시스템이다. 유한 평면 기하학에는 크게 아핀 기하학과 사영 기하학의 두 가지 주요 종류가 있다.^[1] 아핀 평면에서는 우리가 일반적으로 생각하는 평행선의 개념이 적용된다.^[1] 반면, 사영 평면에서는 어떤 두 선이라도 반드시 유일한 점에서 만나기 때문에 평행선이라는 개념 자체가 존재하지 않는다.^[1] 유한 아핀 평면과 유한 사영 평면은 각각 간단한 공리들을 통해 정의될 수 있다.^[1]

3. 1. 유한 아핀 평면

유한 평면 기하에는 아핀 평면 기하와 사영 평면 기하의 두 종류가 있다. 유한 아핀 평면 기하에서는 평행선의 개념이 존재하지만, 유한 사영 평면 기하에서는 임의의 두 선이 항상 한 점에서 만나므로 평행선이 존재하지 않는다.^[1]^[2]

유한 아핀 평면은 다음 공리를 만족하는 점의 집합 ''X''와 ''X''의 부분집합인 선의 집합 ''L''로 구성된다.^[3]

# 서로 다른 두 점 P, Q가 주어졌을 때, P와 Q를 모두 포함하는 선은 정확히 하나 존재한다.

# 플레이페어의 공리: 어떤 선 ''l''과 그 위에 있지 않은 점 ''p''가 주어졌을 때, ''p''를 지나면서 ''l''과 만나지 않는(평행한) 선 ''l'''은 정확히 하나 존재한다. (''l'' ∩ ''l''' = ∅)

# 동일 직선 위에 있지 않은 네 점이 존재한다. (즉, 세 점이 한 직선 위에 있지 않은 네 점의 집합이 존재한다.)

마지막 공리는 기하학이 공집합이거나 모든 점이 한 선 위에 있는 경우처럼 너무 단순해지는 것을 방지하여 자명하지 않음을 보장한다.^[3] 처음 두 공리는 아핀 기하학의 핵심적인 특징을 나타낸다.^[3]

가장 간단한 유한 아핀 평면은 점이 4개뿐인 위수 2의 아핀 평면이다.^[4] 어떤 세 점도 한 선 위에 있지 않으므로, 임의의 두 점은 유일한 선을 결정한다. 이 평면에는 총 6개의 선이 존재한다.^[4] 이는 각 면의 모서리들을 선으로 보고 서로 만나지 않는 모서리들을 평행하다고 간주하는 사면체 구조나, 마주보는 변뿐만 아니라 두 대각선도 평행하다고 간주하는 정사각형 구조에 비유될 수 있다.^[4]

위수 3의 아핀 평면은 9개의 점과 12개의 선으로 이루어져 있으며, 헤세 배치로 알려져 있기도 하다.^[5]

일반적으로, 위수 ''n''의 유한 아핀 평면은 ''n''²개의 점과 ''n''² + ''n''개의 선을 가진다.^[6] 각 선 위에는 정확히 ''n''개의 점이 있으며, 각 점을 지나는 선은 정확히 ''n'' + 1개이다.^[6]

3. 2. 유한 사영 평면

유한 평면 기하학에는 아핀 평면과 사영 평면 두 가지 주요 종류가 있다. 아핀 평면에서는 평행선의 일반적인 의미가 적용되지만, 유한 사영 평면에서는 임의의 두 선이 항상 유일한 점에서 만나므로 평행선이 존재하지 않는다. 유한 사영 평면 기하학은 다음의 간단한 공리들로 정의된다.

# 서로 다른 두 점에 대해, 두 점을 모두 포함하는 선은 정확히 하나 존재한다.

# 서로 다른 두 선의 교점은 정확히 한 점을 포함한다.

# 동일한 선 위에 있지 않은 네 개의 점 집합이 존재한다.

처음 두 공리는 점과 선의 역할이 거의 대칭적임을 보여준다. 이는 사영 평면 기하학에서 쌍대성 원리가 성립함을 의미한다. 즉, 어떤 참인 명제에서 점과 선의 역할을 바꾸어도 여전히 참인 명제가 된다. 세 번째 공리는 최소 4개의 점이 필요함을 명시하지만, 처음 두 공리까지 만족하려면 최소 7개의 점이 필요하다.

세 공리를 모두 만족하는 가장 작은 기하학 구조는 7개의 점과 7개의 선으로 이루어진다. 이 평면에서는 각 점이 3개의 선 위에 있고, 각 선은 3개의 점을 포함한다. 이 가장 간단한 유한 사영 평면을 '''파노 평면'''(Fano plane)이라고 부른다. 파노 평면은 동형인 구조까지 고려하면 유일하며, '''위수'''(order) 2의 사영 평면이라고 불린다. 파노 평면에서 임의의 선 하나와 그 선 위의 점들을 제거하면, 그 결과는 위수 2의 아핀 평면이 된다.

일반적으로, 위수 ''n''의 유한 사영 평면은 ''n''² + ''n'' + 1개의 점과 동일한 개수의 선을 가진다. 또한, 각 선은 ''n'' + 1개의 점을 포함하고, 각 점은 ''n'' + 1개의 선 위에 있다.

파노 평면의 7개 점에 대한 순열 중에서, 같은 선 위의 점들을 항상 같은 선 위로 옮기는 변환을 공선 변환(collineation)이라고 한다. 이러한 변환들의 집합은 군을 이루며, 이를 파노 평면의 대칭군이라고 한다. 이 군의 위수(크기)는 168이며, 단순군 PSL(2,7) (또는 PSL(3,2)) 및 일반 선형군 GL(3,2)와 동형이다.

3. 3. 평면의 위수

'''위수''' ''n''의 유한 평면은 각 선이 ''n''개의 점을 가지는 아핀 평면 또는 각 선이 ''n'' + 1개의 점을 갖는 사영 평면을 말한다. 유한 기하학의 주요 미해결 문제 중 하나는 다음과 같다.

:유한 평면의 위수는 항상 소수 거듭제곱인가?

이는 참일 것으로 추측된다.

위수 ''n''의 아핀 평면과 사영 평면은 ''n'' = ''p''^''k''개의 원소를 가진 유한체 위에 아핀 평면과 사영 평면을 구성하여 만들 수 있으므로, ''n''이 소수 거듭제곱(소수가 양의 정수 지수로 거듭제곱된 값)일 때는 항상 존재한다. 유한체에서 파생되지 않은 평면도 존재하지만(예:

n=9

의 경우), 현재까지 알려진 모든 유한 평면의 위수는 소수 거듭제곱이다.^[1]

이 문제에 대한 가장 중요한 일반적인 결과는 1949년에 증명된 브루크-라이저 정리이다. 이 정리는 다음과 같이 기술된다.^[9]

:만약 정수 ''n''이 4''k'' + 1 또는 4''k'' + 2 형태의 양의 정수이고, ''n''이 두 정수의 제곱의 합으로 표현될 수 없다면, 위수 ''n''의 유한 평면은 존재하지 않는다.

소수 거듭제곱이 아니면서 브룩-라이저 정리로 존재 여부를 판별할 수 없는 가장 작은 정수는 10이다. 10은 4''k'' + 2 형태(10 = 4 × 2 + 2)이지만, 두 정수의 제곱의 합(10 = 1² + 3²)으로 표현 가능하기 때문이다. 위수 10의 유한 평면이 존재하지 않는다는 사실은 1989년에 완료된 컴퓨터 지원 증명을 통해 증명되었다.^[10]

브룩-라이저 정리가 적용되지 않는 다음으로 작은 정수는 12이며, 위수 12의 유한 평면의 존재 여부는 아직 증명되지 않았다.

4. 3차원 이상의 유한 기하

유한 기하학은 2차원 평면뿐만 아니라 3차원 이상의 고차원 공간에서도 다루어진다. 유한 ''평면'' 기하학과 고차원 유한 공간의 기하학 사이에는 몇 가지 중요한 차이점이 존재한다.^[11] 고차원 유한 공간(차원 $n \geq 3$ )에 대한 연구는 수학 이론의 여러 분야에서 중요한 응용을 가진다.

3차원 이상의 유한 사영 공간을 이해하는 데 핵심적인 정리는 베블렌과 영이 증명한 베블렌-영 정리이다.^[11] 이 정리에 따르면, 차원이 3 이상( $k \geq 3$ )인 모든 공리적으로 구성된 사영 공간은 어떤 사체 위의 $k$ 차원 사영 공간 $PG(k, q)$ 와 동형이다. 이 정리는 유한 평면 기하(2차원)와 그보다 높은 차원의 유한 기하 사이에 근본적인 차이가 있음을 보여준다. 평면 기하학에서는 이 정리가 성립하지 않는 비-데자르그 평면과 같은 다양한 구조가 존재할 수 있지만, 3차원 이상에서는 공간의 구조가 유한체 위의 벡터 공간 구조와 필연적으로 연결된다.

일반적으로 모든 체 $K$ 에 대해, 점, 직선, 평면을 각각 체 $K$ 위의 4차원 벡터 공간에서의 1, 2, 3차원 부분 공간으로 간주하여 3차원 사영 공간을 정의할 수 있다. 사영 공간은 점과 선을 기본적인 요소로 하고, 특정 공리들(결합 공리와 존재 공리)을 만족하도록 구성된다.^[11] 예를 들어, 서로 다른 두 점은 유일한 직선을 결정한다는 공리(P-1, P-2), 세 점의 공선성에 관한 파슈의 공리와 유사한 공리(P-3), 직선과 점의 존재에 관한 공리(P-4, P-5, P-6), 모든 점이 동일 평면이나 동일 직선 위에 있지 않다는 공리(P-7, P-6) 등이 있다. 3차원 공간의 경우 모든 점이 해당 3차원 공간( $S_3$ ) 위에 있다는 공리(P-8)가 추가된다.

가장 작은 3차원 사영 공간의 예시는 유한체 GF(2) 위에서 정의되는 공간(PG(3,2))으로, 이는 1892년 지노 파노에 의해 처음 연구되었다. 이러한 3차원 공간의 구체적인 구조와 성질은 하위 섹션에서 더 자세히 다루어진다.

유한 기하학은 3차원을 넘어 더 높은 차원으로 확장될 수 있다. 예를 들어 4차원 사영 기하는 3차원 공리 P-8을 '모든 점이 동일한 3-공간( $S_3$ )에 있지는 않다'(P-8')는 공리와 '모든 점은 4-공간( $S_4$ ) 위에 있다'(P-8")는 공리로 대체하여 정의할 수 있다. 일반적으로 $n$ 차원 사영 기하(차원 $n \geq 4$ )는 P-8을 다음과 같은 두 공리로 대체하여 얻는다: (i) 모든 점이 동일한 $S_3, S_4, \ldots, S_{n-1}$ 위에 있지는 않다. (ii) 모든 점은 $n$ -공간( $S_n$ ) 위에 있다. 이러한 고차원 유한 공간에 대한 연구는 J.W.P. 허쉬펠드 등의 수학자들에 의해 깊이 다루어졌으며,^[11] 현대 수학의 여러 분야에서 중요한 응용을 찾고 있다.

4. 1. 유한 3차원 공간

가장 작은 3차원 사영 공간은 갈루아 체 GF(2) 위에서 정의되며, PG(3,2)로 표기한다. 이 공간은 15개의 점, 35개의 선, 15개의 평면으로 구성된다.

각 평면은 7개의 점과 7개의 선을 포함하며, 기하학적으로 파노 평면과 동형이다. 모든 점은 7개의 선 위에 놓이고, 모든 선은 3개의 점을 포함한다. 또한, 서로 다른 두 점은 정확히 하나의 선 위에 있으며, 서로 다른 두 평면은 정확히 하나의 선에서 교차한다.

이 구조는 1892년 지노 파노(Gino Fano)에 의해 처음 연구되었다. PG(3,2)는 유명한 조합론 문제인 커크만의 여학생 문제의 해답을 구성하는 데 사용될 수 있다. 이 문제는 "15명의 여학생이 매일 3명씩 5개 조로 나뉘어 걷는다. 일주일 동안 모든 여학생이 다른 모든 여학생과 정확히 한 번 같은 조에서 걷도록 조를 편성하라"는 내용이다.

PG(3,2)에서 스프레드는 15개의 점을 서로 만나지 않는 5개의 선(각 선은 3개의 점을 가짐)으로 나누는 것을 의미하며, 이는 특정 날의 여학생 조 편성에 해당한다. PG(3,2)의 ''패킹''은 35개의 선 전체를 7개의 서로 다른 스프레드로 나누는 것을 의미하며, 이는 일주일 동안의 전체 조 편성에 해당한다. 이 문제의 동형이 아닌 7가지 해답 중 2가지가 PG(3,2)의 패킹 구조를 이용하여 표현될 수 있다.

5. 응용

유한 기하학은 조합론이나 부호 이론의 각종 문제에 대해 그 해의 모델을 제공한다. 유명한 예로 커크먼의 여학생 문제^[12] 등이 있다.

참조

_[1] 서적 Discrete Mathematics Using Latin Squares https://books.google[...] John Wiley & Sons 1998-09-17
_[2] 간행물 Sui postulati fondamentali della geometria proiettiva
_[3] 문서
_[4] 문서 Finite Geometries? an AMS Featured Column
_[5] 논문 Finite Projective Geometries https://www.ams.org/[...] 1906
_[6] 문서
_[7] 문서
_[8] 문서
_[9] 문서
_[10] 문서
_[11] 문서
_[12] 웹사이트 Problem 31: Kirkman's schoolgirl problem http://home.wlu.edu/[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com