일차 독립 집합

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
- 2.1. 무한 집합의 경우
3. 성질
4. 기하학적 예시
5. 판단 방법
- 5.1. 행렬식
- 5.2. 가우스 소거법
6. 응용
참조

1. 개요

일차 독립 집합은 체 위의 벡터 공간에서, 벡터들의 일차 결합이 영벡터가 되도록 하는 스칼라들이 모두 0일 경우의 부분 집합을 의미한다. 일차 독립이 아닌 집합은 일차 종속 집합이라 칭한다. 무한 집합의 경우, 모든 유한 부분 집합이 일차 독립이면 일차 독립으로 정의된다. 일차 독립인 벡터들은 영벡터를 포함하지 않으며, 기저를 형성하는 데 사용된다. 일차 독립 개념은 벡터 공간의 차원을 결정하고, 기저를 찾으며, 선형 변환을 이해하는 데 응용된다.

더 읽어볼만한 페이지

선형대수학 - 벡터 공간
벡터 공간은 체 위의 가군으로 정의되는 대수적 구조로, 벡터 덧셈과 스칼라 곱셈 연산을 가지며 특정 공리들을 만족하고, 기저, 차원, 선형 사상 등의 개념을 통해 수학과 물리학 등 다양한 분야에서 활용된다.
선형대수학 - 선형 결합
선형 결합은 벡터 공간에서 벡터들의 스칼라 곱의 합으로 표현되는 식으로, 벡터 집합의 선형 독립성 판단 및 부분 공간 생성과 관련되며, 계수 제약을 통해 다양한 종류의 결합을 정의할 수 있고, 위상 벡터 공간이나 가군으로 일반화될 수 있다.

일차 독립 집합

2. 정의

체 ''K'' 위의 벡터 공간 ''V''의 부분 집합 ''I''에 대하여, 다음 조건들은 서로 동치이며, 이를 만족시키는 ''I''를 ''V''의 '''일차 독립 집합'''이라고 한다.

임의의 서로 다른 $i_1,\dots,i_n\in I$ 및 $c_1,\dots,c_n\in K$ 에 대하여, 만약 $c_1i_1+\cdots+c_ni_n=0_V$ 라면, $0_K=c_1=\cdots=c_n$ 이다. (여기서 $0_V\in V$ 와 $0_K\in K$ 는 각각 $V$ 와 $K$ 의 덧셈 항등원이다.)
임의의 $i\in I$ 에 대하여, $i\not\in\operatorname{Span}_K(I\setminus\{i\})$ 이다. (여기서 $\operatorname{Span}_K(-)$ 는 주어진 부분 집합으로 생성된 부분 벡터 공간이다.)

300px

두 조건의 동치는 체의 모든 0이 아닌 원소가 가역원이라는 성질에 의존하며, 일반적인 환 위의 가군에서는 첫 번째 조건이 두 번째 조건을 함의한다. 일차 독립 집합이 아닌 벡터 공간의 부분 집합을 '''일차 종속 집합'''(linearly dependent set^영어) 또는 '''선형 종속 집합'''이라고 한다.

벡터 공간 ''V''의 벡터 수열

\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_k

에 대해, 다음을 만족하는 스칼라

a_1, a_2, \dots, a_k

가 모두 0이 아니게 존재하면, 해당 수열을 ''선형 종속''이라고 한다.

:

a_1\mathbf{v}_1 + a_2\mathbf{v}_2 + \cdots + a_k\mathbf{v}_k = \mathbf{0},

여기서

\mathbf{0}

은 영벡터를 나타낸다. 이는 적어도 하나의 스칼라가 0이 아니라는 것을 의미하며, 예를 들어

a_1\ne 0

이라고 하면, 위의 식은 다음과 같이 쓸 수 있다.

:

\mathbf{v}_1 = \frac{-a_2}{a_1}\mathbf{v}_2 + \cdots + \frac{-a_k}{a_1} \mathbf{v}_k,

벡터 수열

\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n

이 선형 종속이 아닐 때, 즉, 다음 방정식을

:

a_1\mathbf{v}_1 + a_2 \mathbf{v}_2 + \cdots + a_n\mathbf{v}_n = \mathbf{0},

i=1,\dots,n

에 대해

a_i=0

일 때만 만족될 때, 이를 ''선형 독립''이라고 한다. 이는 수열 내의 어떤 벡터도 수열의 나머지 벡터들의 선형 결합으로 표현될 수 없음을 의미한다.^[2]

임의의 벡터들에 대하여

:

0 \boldsymbol v_1 + 0 \boldsymbol v_2 + \dotsb + 0 \boldsymbol v_n = \boldsymbol{0}

이다. 이것을 자명한 선형 관계라고 부른다. 이것 이외의 선형 관계가 있는지에 따라 선형 종속, 선형 독립이 된다.

선형 관계

:

c_1 \boldsymbol v_1 + c_2 \boldsymbol v_2 + \dotsb + c_n \boldsymbol v_n = \boldsymbol{0}

에서, 어떤

i

에 대해

c_i \ne 0

일 때,

\boldsymbol v_1, \boldsymbol v_2, \dots, \boldsymbol v_n

은 '''선형 종속'''('''일차 종속''')이라고 한다. 이때

\boldsymbol v_i

는 나머지

n-1

개의 벡터의 선형 결합으로 나타낼 수 있다.

벡터

\boldsymbol v_1, \boldsymbol v_2, \dots, \boldsymbol v_n

가 선형 종속이 아닐 때 이 집합은 '''선형 독립'''('''일차 독립''')이라고 한다.^[5] 즉, 스칼라

a_1, a_2, \dots, a_n

에 대해

:

a_1 \boldsymbol v_1 + a_2 \boldsymbol v_2 + \dotsb + a_n \boldsymbol v_n = \boldsymbol{0} \Rightarrow a_1 = \cdots = a_n =0

이 때, 어떤 벡터도 나머지

n-1

개의 벡터가 생성하는 선형 부분 공간 밖의 벡터이다.

2. 1. 무한 집합의 경우

무한 벡터 집합은 모든 비어 있지 않은 유한 부분 집합이 일차 독립일 경우 일차 독립이라고 정의한다. 반대로, 무한 벡터 집합에 일차 종속인 유한 부분 집합이 있거나, 집합 내의 어떤 벡터가 집합 내 다른 벡터들의 선형 결합일 경우 일차 종속이라고 한다.

벡터의 인덱스족은 같은 벡터를 두 번 포함하지 않고, 그 벡터 집합이 일차 독립이면 일차 독립이다. 그렇지 않으면, 그 족은 일차 종속이라고 한다.

3. 성질

일차 독립 집합의 모든 부분 집합은 일차 독립이다. 반대로, 일차 종속 집합을 포함하는 부분 집합은 일차 종속이다.^[2]
공집합은 벡터 공간의 일차 독립 집합이다.^[2]
체 $K$ 위의 벡터 공간 $V$ 의 한원소 부분 집합 $\{v\}\subseteq V$ 가 일차 독립 집합일 필요충분조건은 $v\ne 0_V$ 이다.^[2] 즉, 영벡터가 아닌 벡터에 대해 일원 집합은 선형 독립이다.
선형 독립인 벡터들은 모두 영벡터가 아니다.^[5]
선형 독립인 집합은 기저로 확장할 수 있다.
벡터 공간 전체를 생성하는 집합의 선형 독립인 부분 집합 전체는 극대원(=기저)을 갖는다.

4. 기하학적 예시

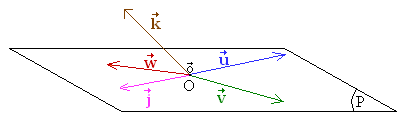
Vectores u|벡터 u^es와 Vectores v|벡터 v^es는 독립적이며 평면 P를 정의한다.
Vectores u|벡터 u^es, Vectores v|벡터 v^es 및 Vectores w|벡터 w^es는 셋 모두 동일한 평면에 포함되어 있으므로 종속적이다.
Vectores u|벡터 u^es와 Vectores j|벡터 j^es는 서로 평행하므로 종속적이다.
Vectores u|벡터 u^es, Vectores v|벡터 v^es 및 Vectores k|벡터 k^es는 Vectores u|벡터 u^es와 Vectores v|벡터 v^es가 서로 독립적이고 Vectores k|벡터 k^es가 이들의 선형 결합이 아니거나, 동등하게는 공통 평면에 속하지 않으므로 독립적이다. 세 벡터는 3차원 공간을 정의한다.
벡터 Vectores o|o^es (영벡터, 그 성분이 0과 같음)와 Vectores k|벡터 k^es는 Vectores o|o^es = 0 Vectores k|k^es이므로 종속적이다.

어떤 장소의 위치를 설명할 때 "여기로부터 북쪽으로 약 4.83km, 동쪽으로 약 6.44km 떨어진 곳에 있습니다."라고 말할 수 있다. 이 정보는 위치를 설명하기에 충분한데, 지리 좌표계는 2차원 벡터 공간으로 간주할 수 있기 때문이다(고도와 지구 표면의 곡률을 무시). "그곳은 여기서 북동쪽으로 약 8.05km 떨어져 있습니다."라고 덧붙일 수 있지만, 이 마지막 진술은 ''참''이지만 위치를 찾는 데는 필요하지 않다.

이 예에서 "북쪽으로 약 4.83km" 벡터와 "동쪽으로 약 6.44km" 벡터는 일차 독립이다. 즉, 북쪽 벡터는 동쪽 벡터로 설명될 수 없고 그 반대도 마찬가지이다. 세 번째 "북동쪽으로 약 8.05km" 벡터는 다른 두 벡터의 선형 결합이며, 이는 벡터 집합을 ''선형 종속''으로 만든다. 다시 말해, 세 벡터 중 하나는 평면에서 특정 위치를 정의하는 데 불필요하다.

고도를 무시하지 않으면, 일차 독립 집합에 세 번째 벡터를 추가해야 한다. 일반적으로, n차원 공간의 모든 위치를 설명하려면 n개의 일차 독립 벡터가 필요하다.

차원보다 더 많은 벡터가 존재하면, 그 벡터들은 선형 종속이다. 이는

\R^2

에서 세 개의 벡터를 예로 들어 위에서 설명했다.

5. 판단 방법

n개의 벡터가 Rⁿ에 속할 때, 이 벡터들을 열로 하는 행렬의 행렬식이 0이 아니면 그 벡터들은 일차 독립이다. 또는, 벡터들을 행으로 하는 행렬을 만들어 가우스 소거법을 적용하여 기약 사다리꼴 행렬로 변환했을 때 모든 열에 선행 성분(pivot)이 존재하면 일차 독립이다.

5. 1. 행렬식

n개의 벡터가 Rⁿ에 속할 때, 이 벡터들을 열로 하는 행렬의 행렬식이 0이 아니면 그 벡터들은 일차 독립이다.

예를 들어, R²의 벡터 (1, 1)과 (-3, 2)를 생각해보자. 이 벡터들을 열로 하는 행렬은 다음과 같다.

:

A = \begin{bmatrix}1&-3\\1&2\end{bmatrix} . \,\!

이 행렬 A의 행렬식은 다음과 같이 계산된다.

:

\det A = 1\cdot2 - 1\cdot(-3) = 5 \ne 0 . \,\!

행렬식이 0이 아니므로, 벡터 (1, 1)과 (-3, 2)는 일차 독립이다.^[1]

5. 2. 가우스 소거법

벡터들을 행으로 하는 행렬을 만들어 가우스 소거법을 적용하여 기약 사다리꼴 행렬로 변환한다. 모든 열에 선행 성분(pivot)이 존재하면 일차 독립이다.

\mathbb{R}^4

의 세 벡터

\mathbf{v}_1= \begin{bmatrix}1\\4\\2\\-3\end{bmatrix},  \mathbf{v}_2=\begin{bmatrix}7\\10\\-4\\-1\end{bmatrix}, \mathbf{v}_3=\begin{bmatrix}-2\\1\\5\\-4\end{bmatrix}

가 일차 종속인지 여부를 판단하기 위해 다음과 같은 행렬 방정식을 구성한다.

:

\begin{bmatrix}1&7&-2\\4& 10& 1\\2&-4&5\\-3&-1&-4\end{bmatrix}\begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix} =  \begin{bmatrix}0\\0\\0\\0\end{bmatrix}.

이 방정식을 행 연산하여 다음과 같이 변환한다.

:

\begin{bmatrix} 1& 7 & -2 \\ 0& -18& 9\\ 0 & 0 & 0\\ 0& 0& 0\end{bmatrix} \begin{bmatrix} a_1\\ a_2 \\ a_3 \end{bmatrix} =  \begin{bmatrix}0\\0\\0\\0\end{bmatrix}.

v₃에 대해 풀기 위해 재정렬하면,

:

\begin{bmatrix} 1& 7 \\ 0& -18 \end{bmatrix} \begin{bmatrix} a_1\\ a_2  \end{bmatrix} =  -a_3\begin{bmatrix}-2\\9\end{bmatrix}.

이 방정식은 다음과 같이 0이 아닌 ''a''_i를 정의하기 위해 쉽게 풀린다.

:

a_1 = -3 a_3 /2,  a_2 = a_3/2,

여기서

a_3

는 임의로 선택할 수 있다. 따라서, 벡터

\mathbf{v}_1, \mathbf{v}_2,

및

\mathbf{v}_3

는 일차 종속이다.

6. 응용

일차 독립은 벡터 공간의 차원을 결정하는 데 사용된다. 기저를 찾고, 벡터 공간을 효율적으로 표현하는 데 사용된다. 선형 변환의 핵(kernel)과 상(image)을 이해하는 데 중요한 역할을 한다.

참조

_[1] 서적 Linear Algebra https://books.google[...] Dover Publications 1977
_[2] 서적 Linear Algebra Pearson, 4th Edition
_[3] 서적 Matching Theory North-Holland
_[4] 서적 Functional Analysis Dover Publications
_[5] 서적 Linear Algebra Pearson, 4th Edition

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com