입맞춤 수 문제

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 차원별 입맞춤 수
3. 알려진 입맞춤 수의 범위
4. 일반화
5. 수학적 표현
참조

1. 개요

입맞춤 수 문제는 주어진 구에 겹치지 않게 접촉하는 동일한 크기의 구의 최대 개수를 찾는 문제로, 1차원에서 2개, 2차원에서 6개, 3차원에서 12개, 4차원에서 24개로 알려져 있다. 이 문제는 1694년 뉴턴과 데이비드 그레고리의 논쟁에서 시작되어 1953년에 3차원 입맞춤 수가 증명되었으며, 4차원 이상에서는 8차원과 24차원에서 각각 E8 격자와 리치 격자로 알려져 있다. 이 문제는 일반화될 수 있으며, 수학적 표현과 다양한 차원에서의 알려진 입맞춤 수의 범위를 나타내는 표가 제시된다.

더 읽어볼만한 페이지

이산기하학 - 최근접 이웃 탐색
최근접 이웃 탐색은 다차원 공간에서 주어진 질의와 가장 유사한 데이터를 찾는 최적화 문제로, 데이터 압축, 데이터 마이닝, 기계 학습 등 다양한 분야에서 활용되며, 효율적인 탐색을 위해 다양한 알고리즘이 개발되고 있고, 개인 정보 보호 및 데이터 편향성과 같은 윤리적 문제에 대한 고려도 중요해지고 있다.
이산기하학 - 보로노이 다이어그램
보로노이 다이어그램은 거리 공간에서 점 집합을 기반으로 공간을 분할하는 기하학적 구조이며, 각 점까지의 거리가 가장 가까운 공간 영역인 보로노이 셀들의 집합을 의미하고 다양한 분야에서 활용된다.
유클리드 기하학 - 결정계
결정계는 결정 구조의 대칭성에 따라 7가지(삼사, 단사, 사방, 정방, 삼방, 육방, 입방)로 분류되며, 각 결정계는 고유한 대칭 요소와 점군의 대칭성을 갖는다.
유클리드 기하학 - 퐁슬레-슈타이너 정리
퐁슬레-슈타이너 정리는 자와 주어진 원(중심 포함)만 사용하여 자와 컴퍼스로 작도 가능한 모든 것을 작도할 수 있다는 기하학적 정리이다.

입맞춤 수 문제
개요
정의	n차원 공간에서 반지름이 같은 n차원 초구들이 한 초구의 표면에 동시에 접할 수 있는 최대 초구의 수
다른 이름	접촉수, 조정수
값
1차원	2
2차원	6
3차원	12
4차원	24
8차원	240
24차원	196,560
탐구
난제	3차원과 그 외 차원에서의 정확한 값을 찾는 것이 난제임
상한 및 하한	상한과 하한은 알려져 있지만, 정확한 값은 모르는 경우가 많음
응용
분야	구면 코딩 오류 수정 부호 양자 정보 이론
관련 개념	구 충전

2. 차원별 입맞춤 수

1차원에서는 입맞춤 수가 2, 2차원에서는 6, 3차원에서는 12, 4차원에서는 24이다. 3차원의 경우 아이작 뉴턴은 12, 데이비드 그레고리(David Gregory)는 13이라고 생각했으나, 1953년에 12로 증명되었다.^[19]^[20] 4차원의 경우 2003년에 24로 증명되었다.^[21]^[22]

4차원 이상에서는 8차원과 24차원에서 입맞춤 수가 알려져 있는데, 각각 E₈ 격자와 리치 격자라고 불린다.

2018년 기준으로 다양한 차원에서 입맞춤 수의 가능한 범위는 다음 표와 같다.^[18] 굵게 표시된 차원은 입맞춤 수가 확정된 차원이다.

차원	하한	상한
1	2
2	6
3	12
4	24
5	40	44
6	72	78
7	126	134
8	240
9	306	363
10	500	553
11	582	869
12	840	1356
13	1154	2066
14	1606	3177
15	2564	4858
16	4320	7332
17	5346	11014
18	7398	16469
19	10668	24575
20	17400	36402
21	27720	53878
22	49896	81376
23	93150	123328
24	196560

2. 1. 1차원

1차원에서는 자명하게 2이다.^[2]

2. 2. 2차원

2차원에서 입맞춤 수는 6이다.

'''증명''': 중심이 ''C''인 원이 중심이 ''C''₁, ''C''₂, ... 인 원들에 의해 접한다고 가정한다. ''C'' ''C''_''i'' 광선을 생각해보면, 이 광선들은 모두 같은 중심 ''C''에서 나오므로, 인접한 광선 사이의 각도의 합은 360°이다.

6개 이상의 접하는 원이 있다고 가정하면, 적어도 두 개의 인접한 광선, 즉 ''C'' ''C''₁과 ''C'' ''C''₂가 60° 미만의 각도로 분리된다. 모든 ''i''에 대해 ''C C_i'' 선분은 2''r''로 동일한 길이를 갖는다. 따라서 삼각형 ''C'' ''C''₁ ''C''₂는 이등변 삼각형이며, 세 번째 변인 ''C''₁ ''C''₂의 변의 길이는 2''r'' 미만이다. 따라서 원 1과 2는 교차하는데, 이는 모순이다.^[3]

2. 3. 3차원

3차원에서의 입맞춤 수는 12이지만, 이 값을 정확하게 증명하는 것은 1차원이나 2차원보다 훨씬 어려웠다. 아이작 뉴턴은 12개가 최대라고 생각한 반면, 데이비드 그레고리는 13개도 가능하다고 주장했다. 이 문제는 1694년 뉴턴과 그레고리 사이의 유명한 논쟁 주제였으나, 19세기에 뉴턴이 옳다는 불완전한 증명들이 나왔고, 라인홀트 호페의 증명도 그중 하나였다. 하지만 최초의 정확한 증명은 1953년에야 발표되었다.^[4]^[5]^[6]^[17]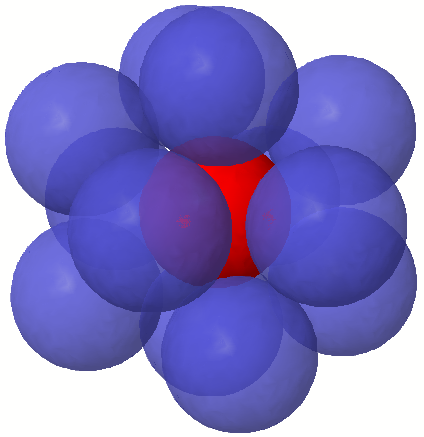

중심 구에 12개의 구를 배치하는 것은 쉽지만, 공간이 많이 남아 13번째 구를 추가할 수 없다는 것을 명확하게 알기는 어려웠다. 실제로 12개의 외부 구 중 어느 두 개든 중심 구와의 접촉을 유지하면서 위치를 바꿀 수 있을 정도로 여유 공간이 많았다.

3차원에서 12개의 이웃은 모든 원자가 동일한 크기를 갖는 결정 격자에서 원자의 최대 배위수에 해당한다. 배위수 12는 입방 밀집 구조 또는 육방 밀집 구조에서 나타난다.

2. 4. 4차원 이상

4차원에서는 24개 또는 25개가 가능하다고 생각되었다. 24개를 인접하게 배치하는 것은 어렵지 않다. 2003년 올레그 무신(Oleg Musin)이 24개가 최대임을 증명하였다.^[7]^[8]^[21]^[22]

4차원 이상에서는 8차원과 24차원에서 입맞춤 수가 알려져 있으며, 각각 E₈ 격자와 리치 격자라고 불린다. 8차원에서의 입맞춤 수는 240이고, 24차원에서는 196,560이다.^[9]^[10] 다른 차원에서는 ''n'' 차원에서의 입맞춤 수가 알려져 있지 않다.

구의 중심이 모두 격자의 점에 있는 ''격자'' 배열로 제한할 경우, 이 제한된 입맞춤 수는 ''n'' = 1부터 9까지, 그리고 ''n'' = 24 차원에서 알려져 있다.^[11] 5, 6, 7 차원의 경우, 현재까지 알려진 가장 높은 입맞춤 수를 가진 배열은 최적의 격자 배열이지만, 더 높은 입맞춤 수를 가진 비격자 배열이 존재할 가능성은 배제되지 않았다.

2018년을 기준으로 다양한 차원에서 입맞춤 수의 가능한 범위는 아래 표와 같다.^[18] 굵게 표시된 차원은 입맞춤 수가 확정된 차원이다.

차원	하한	상한
1	2
2	6
3	12
4	24
5	40	44
6	72	78
7	126	134
8	240
9	306	363
10	500	553
11	582	869
12	840	1356
13	1154	2066
14	1606	3177
15	2564	4858
16	4320	7332
17	5346	11014
18	7398	16469
19	10668	24575
20	17400	36402
21	27720	53878
22	49896	81376
23	93150	123328
24	196560

3. 알려진 입맞춤 수의 범위

1차원에서는 2, 2차원에서는 6, 3차원에서는 12이다. 3차원의 경우 아이작 뉴턴은 12, 데이비드 그레고리(David Gregory)는 13이라고 생각했으나, 1953년에 12개가 최대라는 엄밀한 증명이 나왔다.^[19]^[20] 4차원에서는 24개가 최대라는 것이 2003년에 증명되었다.^[21]^[22]

8차원과 24차원에서는 입맞춤 수가 알려져 있는데, 각각 E₈ 격자와 리치 격자에 해당한다.

다음 표는 다양한 차원에서 입맞춤 수의 알려진 범위를 나타낸다.^[12] 입맞춤 수가 정확히 알려진 차원은 굵은 글씨로 표시되어 있다.

차원	하한	상한
1	2
2	6
3	12
4	24^[7]
5	40	44
6	72	77
7	126	134
8	240
9	306	363
10	510	553
11	592	868
12	840	1,355
13	1,154	2,064
14	1,932	3,174
15	2,564	4,853
16	4,320	7,320
17	5,346	10,978
18	7,398	16,406
19	10,668	24,417
20	17,400	36,195
21	27,720	53,524
22	49,896	80,810
23	93,150	122,351
24	196,560

4. 일반화

입맞춤 수 문제는 주어진 물체에 접하는 모든 합동인 사본의 최대 개수를 찾는 문제로 일반화할 수 있다. 사본이 원래 물체와 합동이기만 하면 되는지, 원래 물체의 평행 이동인지, 또는 격자에 의해 이동되는지에 따라 문제의 여러 가지 변형이 있다. 예를 들어 정사면체의 경우, 격자 입맞춤 수와 이동 입맞춤 수는 모두 18로 같지만, 합동 입맞춤 수는 최소 56이다.^[13]

5. 수학적 표현

키스 수 문제는 일련의 부등식의 해의 존재로 표현될 수 있다. $x_n$ 을 구의 중심을 나타내는 ''N''개의 ''D''차원 위치 벡터 집합이라고 할 때, 이 구 집합이 겹치지 않게 중심 구 주위에 놓일 수 있는 조건은 다음과 같다:^[15]

: $\exist x\ \left\{ \forall_n \{x_n^\textsf{T} x_n = 1\} \land \forall_{m,n: m \neq n} \{ (x_n - x_m)^\textsf{T}(x_n - x_m) \geq 1\} \right\}$

따라서 각 차원에 대한 문제는 실수 존재 이론으로 표현될 수 있다. 그러나 이 형태의 문제를 해결하는 일반적인 방법은 최소한 지수 시간이 걸리므로, 이 문제는 최대 4차원까지만 해결되었다. 추가 변수 $y_{nm}$ 을 추가하면, 이는 ''N''(''N'' − 1)/2 + ''DN'' 변수의 단일 4차 방정식으로 변환될 수 있다:^[16]

: $\exist xy\ \left\{ \sum_n \left(x_n^\textsf{T} x_n - 1\right)^2 + \sum_{m,n: m$

''D'' = 5 차원과 ''N'' = 40 + 1 벡터의 경우를 해결하는 것은 1025개의 변수를 가진 4차 다항식의 실수 해의 존재를 결정하는 것과 같다. ''D'' = 24 차원 및 ''N'' = 196560 + 1의 경우, 4차 방정식은 19,322,732,544개의 변수를 갖게 된다. 거리 기하학 측면에서의 대안적인 표현은 ''m''^번째 구와 ''n''^번째 구 사이의 제곱 거리 $R_{mn}$ 으로 주어진다.

: $\exist R\ \{ \forall_n \{R_{0n} = 1 \} \land \forall_{m,n: m$

이는 케일리-멩거 행렬식이 ''D'' 차원에서 (''D'' + 1) 단체를 형성하는 임의의 점 집합에 대해 0이 되는 조건으로 보완되어야 한다. 왜냐하면 그 부피는 0이어야 하기 때문이다. $R_{mn} = 1 + {y_{mn}}^2$ 으로 설정하면 실수 값에 대해서만 풀어야 하는 ''y''에 대한 일련의 연립 다항식 방정식이 생성된다. 완전히 동일한 두 가지 방법은 다양한 용도로 사용된다. 예를 들어, 두 번째 경우에서는 ''y''에 대한 다항식을 최소화하기 위해 ''y''의 값을 작은 양만큼 무작위로 변경해 볼 수 있다.

참조

_[1] 논문 High accuracy semidefinite programming bounds for kissing numbers
_[2] 문서
_[3] 논문 Simple heuristics for unit disk graphs
_[4] 서적 Sphere Packings, Lattices and Groups Springer-Verlag
_[5] 서적 Research problems in discrete geometry Springer
_[6] 서적 Surveys on Discrete and Computational Geometry: Twenty Years Later (AMS-IMS-SIAM Joint Summer Research Conference, June 18ÔÇô22, 2006, Snowbird, Utah) American Mathematical Society
_[7] 논문 The problem of the twenty-five spheres
_[8] 논문 Kissing numbers, sphere packings, and some unexpected proofs https://www.ams.org/[...] 2004-09
_[9] 논문 О границах для упаковок в n-мерном евклидовом пространстве
_[10] 논문 New bounds on the number of unit spheres that can touch a unit sphere in n dimensions 1979
_[11] 웹사이트 Kissing Number
_[12] 논문 Improving the Semidefinite Programming Bound for the Kissing Number by Exploiting Polynomial Symmetry
_[13] 논문 Mysteries in packing regular tetrahedra https://www.ams.org/[...] 2012-12
_[14] 논문 Approximation Algorithms for Intersection Graphs https://opus.bibliot[...] 2012-07
_[15] 문서
_[16] 문서
_[17] 문서
_[18] 논문 Improving the Semidefinite Programming Bound for the Kissing Number by Exploiting Polynomial Symmetry
_[19] 서적 Sphere Packings, Lattices and Groups Springer-Verlag
_[20] 서적 Research problems in discrete geometry Springer
_[21] 논문 The problem of the twenty-five spheres
_[22] 논문 Kissing numbers, sphere packings, and some unexpected proofs http://www.ams.org/n[...] 2004-09

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com