자구

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 자기 구역 이론의 발전
3. 자기 구역 구조
4. 란다우-리프시츠 에너지 방정식 (Landau-Lifshitz energy equation)
5. 자기 구역 관찰 기술
참조

1. 개요

자구(磁區, magnetic domain)는 강자성체나 페리자성체 내에서 자기 모멘트가 정렬된 미세한 영역을 의미한다. 1906년 피에르-에르네스트 바이스는 자기 구역의 존재를 처음으로 제안했고, 이후 펠릭스 블로흐, 루이 네엘 등에 의해 자벽에 대한 설명이 이루어졌다. 자구는 물질의 내부 에너지를 최소화하기 위해 형성되며, 자구의 크기는 재료 내 여러 에너지의 균형에 따라 결정된다. 자구의 구조는 란다우-리프시츠 에너지 방정식을 통해 설명되며, 커 현미경법, 로렌츠 현미경, 자기력 현미경, 비터 방법 등 다양한 기술을 사용하여 관찰할 수 있다.

더 읽어볼만한 페이지

강자성 - 강자성 초전도체
자기 - 상자성
상자성은 외부 자기장이 없을 때는 자성을 띠지 않지만, 외부 자기장이 가해지면 자기장 방향으로 약하게 자화되는 성질을 말하며, 짝을 짓지 않은 전자의 스핀으로 인해 영구 자기 모멘트를 가지는 상자성체가 이러한 특징을 보인다.
자기 - 자석
자석은 내부 자구들의 정렬로 자기장을 생성하는 물체로, N극과 S극을 가지며 영구자석과 전자석으로 나뉘어 나침반, 스피커 등 다양한 분야에 활용된다.

자구
개요
정의	자구(磁區, magnetic domain)는 강자성체나 준강자성체 물질 내에서 자화 방향이 균일한 영역을 의미함.
특징	각 구역 내에서 원자들의 자기 모멘트는 정렬되어 있으며, 이는 구역 전체에 걸쳐 강한 자화를 유발함.
분할 이유	전체 에너지 상태를 최소화하기 위해 자발적으로 분할됨.
에너지 최소화
자구 벽 형성	자구들은 서로 자화 방향이 다른데, 이들 사이에는 비교적 얇은 자구 벽(domain wall)이 형성됨.
에너지 보존	자구 벽 내부의 원자들은 인접한 자구들의 방향으로 점진적으로 회전하며, 이 회전으로 인해 교환 에너지와 이방성 에너지가 증가하지만, 정자계 에너지를 감소시켜 전체 에너지를 최소화함.
자기장 변화에 따른 자구 변화
외부 자기장 인가	외부 자기장이 가해지면 자기장 방향과 평행한 자구는 커지고, 반대 방향의 자구는 작아짐.
자구 벽 이동	충분히 강한 자기장이 가해지면 자구 벽이 이동하여 결정 전체가 하나의 자구로 될 수 있음.
응용
자기 기록 매체	자구의 개념은 하드 디스크 드라이브와 같은 자기 기록 매체에서 정보 저장 원리로 활용됨.
기타	자기 센서, 자기 공명 영상 (MRI) 등 다양한 기술에 응용됨.

2. 자기 구역 이론의 발전

1906년 프랑스 물리학자 피에르-에르네스트 바이스는 강자성체 내에 자기 구역이 존재한다는 가설을 제시했다.^[1]^[2] 바이스는 수많은 원자 자기 모멘트(일반적으로 10¹²-10¹⁸개)가 평행하게 정렬된다고 제안했다. 정렬 방향은 자기 구역마다 다를 수 있지만, 특정 결정 축(용이축)이 자기 모멘트에 의해 선호될 수 있다. 바이스는 강자성 물질 내 원자 모멘트의 자발적 정렬 이유를 설명하기 위해 바이스 평균장(Weiss mean field)을 제시했다. 그는 물질 내의 주어진 자기 모멘트가 이웃의 자화로 인해 매우 높은 유효 자기장을 경험한다고 가정했다.

이후, 양자 이론을 통해 바이스장의 미시적 기원을 이해하게 되었다. 국소 스핀 간의 교환 상호 작용은 인접한 자기 모멘트의 평행(강자성체에서) 또는 반평행(반강자성체에서) 상태를 선호했다.

3. 자기 구역 구조

철과 같은 강자성 물질이 전체적으로 한 방향으로 자화되지 않고, 여러 개의 자기 구역으로 나뉘는 이유는 내부 에너지를 최소화하기 위해서이다.^[3] 큰 강자성 물질이 전체적으로 일정한 자화를 가지면, 외부로 확장되는 큰 자기장이 발생한다 ''(그림 a)''. 이는 자기장 안에 많은 양의 자성 에너지를 저장하게 된다.

이 에너지를 줄이기 위해, 물질은 자화 방향이 반대인 두 개의 자기 구역으로 나뉠 수 있다 ''(그림 b)''. 자기장 선은 각 구역을 통해 반대 방향으로 순환하며, 물질 외부의 자기장을 감소시킨다. 자기장 에너지를 더 줄이기 위해, 각 구역은 다시 더 작은 평행한 구역들로 나뉠 수 있다.

실제 자기 물질의 자구 구조는 큰 자구가 더 작은 자구로 분리되는 방식으로 형성되지는 않는다. 예를 들어, 물질이 퀴리 온도 이하로 냉각되면, 평형 자구 구성이 나타난다. 하지만 자구 분리 개념은 자구 형성 과정에서의 에너지 균형을 설명하는 데 유용하다.

물질이 자기정적 에너지를 더 줄이는 또 다른 방법은, 다른 도메인에 수직으로 자화하는 도메인을 형성하는 것이다 (그림 c).^[3] 이러한 도메인은 "플럭스 폐쇄 도메인"이라고 불리며, 자기력선이 물질 내에서 완전히 닫힌 루프를 형성하여 자기정적 에너지를 0으로 줄인다.

강자성체나 페리자성체 내부의 미세한 영역의 자기 모멘트는 한 방향으로 정렬되어 있으며, 각 영역은 자벽으로 분리되어 있다.

자구는 퀴리 온도 이상이 되면 소멸한다. 1907년 피에르 와이스는 강자성 원자의 자기 모멘트가 외부 자기장이 없어도 금속 결정의 방향과 밀접하게 관련된 방향으로 정렬된다는 것을 발견했다. 1931년 펠릭스 블로흐가 자벽을 설명했고, 이후 루이 네엘은 다른 자벽의 존재를 제시했다. 1935년 레프 란다우와 예브게니 리프시츠가 최초의 현실적인 자구 모델을 제안하고, 란다우-리프시츠-길버트 방정식을 유도했다.

3. 1. 자기 구역의 크기

위에 설명한 바와 같이, 너무 큰 자기 구역은 불안정하여 더 작은 구역으로 분할된다. 하지만 충분히 작은 구역은 안정적이며 분할되지 않는데, 이것이 재료 내에서 생성되는 구역의 크기를 결정한다. 이 크기는 재료 내의 여러 에너지의 균형에 따라 달라진다.^[3] 자화 영역이 두 개의 구역으로 분할될 때마다, 서로 다른 방향을 향하는 자화 자기 쌍극자(분자)가 인접해 있는 구역 벽이 구역 사이에 생성된다. 자화를 생성하는 교환 상호 작용은 인접한 쌍극자를 정렬하여 동일한 방향을 가리키도록 하는 힘이다. 인접한 쌍극자가 서로 다른 방향을 가리키도록 강제하려면 에너지가 필요하다. 따라서 구역 벽에는 구역 벽 에너지라고 하는 추가 에너지가 필요한데, 이는 벽의 면적에 비례한다.

따라서 구역이 분할될 때 에너지가 감소하는 순량은 절약된 자기장 에너지와 구역 벽을 생성하는 데 필요한 추가 에너지의 차이와 같다. 자기장 에너지는 구역 크기의 세제곱에 비례하고, 구역 벽 에너지는 구역 크기의 제곱에 비례한다. 따라서 구역이 작아질수록 분할로 절약되는 순 에너지가 감소한다. 구역은 추가적인 구역 벽을 생성하는 데 드는 에너지 비용이 절약되는 자기장 에너지와 같아질 때까지 더 작은 구역으로 계속 분할된다. 그러면 이 크기의 구역은 안정적이다. 대부분의 재료에서 구역의 크기는 미시적으로, 약 10⁻⁴ - 10⁻⁶ m이다.^[4]^[5]^[6]

3. 2. 자기 이방성 (Magnetic anisotropy)

대부분 자기 재료의 결정 격자는 자기 이방성을 갖는다. 이는 결정 축 중 하나에 평행한 자화의 "쉬운" 방향(easy axis)을 갖는다는 것을 의미한다. 재료의 자화를 다른 방향으로 변경하려면 "자성 결정 이방성 에너지"라고 하는 추가 에너지가 필요하다.^[3]

3. 3. 자왜 (Magnetostriction)

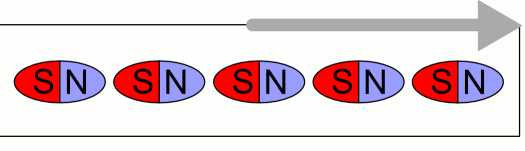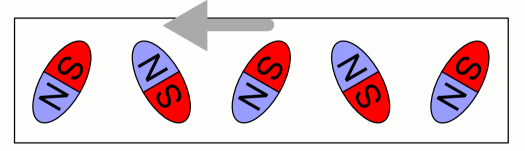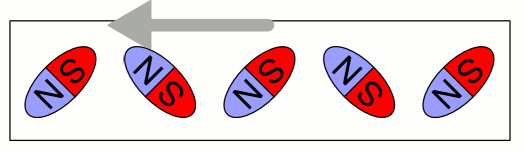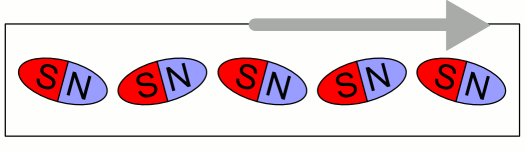
자기변형의 작동 방식을 보여주는 애니메이션. 외부 자기장이 변하면 자기 쌍극자가 회전하여 결정 격자의 치수가 변경된다.

자왜는 자기 물질의 자화 방향이 변경될 때 모양이 약간 변하는 현상이다.^[3] 자기장의 변화는 자기 쌍극자 분자의 모양을 약간 변화시켜, 결정 격자가 한 차원에서는 길어지고 다른 차원에서는 짧아지게 한다. 그러나 자기 도메인은 주변 물질에 의해 경계가 고정되어 "압착"되기 때문에, 실제로 모양이 변할 수는 없다. 대신 자화 방향의 변화는 물질 내에 미세한 기계적 응력을 유발하여, 도메인을 생성하는 데 더 많은 에너지가 필요하게 된다. 이러한 현상을 ''자왜 이방성 에너지''라고 한다.

3. 4. 결정립 구조 (Grain structure)

대부분의 자기 재료는 미세 결정립으로 구성된 다결정질이다. 이 결정립은 자기 구역과 ''같지 않다''. 각 결정립은 작은 결정으로, 개별 결정립의 결정 격자는 임의의 방향으로 정렬되어 있다. 대부분의 재료에서 각 결정립은 여러 자구를 포함할 만큼 충분히 크다. 각 결정은 "용이 자화" 축을 가지며, 자화 축이 이 축에 평행하고 교대로 정렬된 자구로 나뉜다.

자성 재료 표면의 현미경 사진으로, 각 결정립은 자화의 "쉬운" 축에 평행한 여러 자구로 나뉘며, 자화는 교대로 방향을 갖는다 (빨간색과 녹색 영역).

3. 5. "자화" 상태 (Magnetized states)

강자성 물질은 최저 에너지 상태에서는 외부 자기장이 거의 또는 전혀 없는 "비자화" 상태이다. 그러나 도메인은 자화가 대부분 동일한 방향을 가리켜 외부 자기장을 생성하는 다른 구성으로도 존재할 수 있다. 이러한 구성은 최소 에너지 구성은 아니지만, 도메인 벽이 결정 격자 내의 결함에 "고정"되어 에너지가 국소적 최소가 될 수 있으며, 매우 안정적일 수 있다.^[3]

외부 자기장을 물질에 가하면 도메인 벽이 이동하여 자기장과 정렬된 도메인이 성장하고 반대 방향 도메인이 축소될 수 있다. 외부 자기장이 제거되면 도메인 벽은 새로운 방향으로 고정된 채로 유지되고, 정렬된 도메인은 자기장을 생성한다. 이것이 강자성 물질 조각이 "자화"되어 영구 자석이 되는 현상이다.^[3]

자석을 가열하거나, 망치질로 진동을 가하거나, 소자 코일에서 급격하게 진동하는 자기장을 가하면 도메인 벽이 고정된 상태에서 풀리는 경향이 있으며, 외부 자기장이 적은 더 낮은 에너지 구성으로 되돌아가 물질을 "감자"시킨다.^[3]

4. 란다우-리프시츠 에너지 방정식 (Landau-Lifshitz energy equation)

1935년 레프 란다우와 예브게니 리프시츠는 자기 도메인 현대 이론의 기초가 되는 자유 에너지 방정식을 제안했다.^[7] 이 방정식은 자기 재료의 결정에서 깁스 자유 에너지를 최소화하는 도메인 구조를 설명한다. 란다우-리프시츠 자유 에너지 ''E''는 다음과 같은 에너지 항들의 합으로 표현된다:^[8]

: $E = E_{ex} + E_D + E_{\lambda} + E_k + E_H\,$

각 항의 의미는 다음과 같다.

'''''E_ex''''' ('''교환 에너지'''): 강자성, 강자성체, 반강자성 물질 내 자기 쌍극자 분자 간의 교환 상호작용에 의한 에너지다. 모든 쌍극자가 같은 방향을 가리킬 때 가장 낮아, 자기 재료의 자화를 유도한다. 자화 방향이 다른 두 도메인 경계(도메인 벽)에서는 다른 방향을 가리키는 자기 쌍극자들이 인접해 이 에너지가 증가한다. 이 추가 교환 에너지는 도메인 벽의 총 면적에 비례한다.
'''''E_D''''' ('''자기 정전 에너지'''): 샘플 내 한 부분의 자화가 다른 부분에 미치는 상호작용에 의한 자체 에너지다. 도메인 외부로 확장되는 자기장의 부피에 따라 달라진다. 이 에너지는 도메인 외부 자기장 선의 루프 길이를 최소화하면 감소한다. 예를 들어 자화가 샘플 표면에 평행하면 자기장 선이 샘플 외부로 나가지 않아 이 에너지가 줄어든다. 자기 도메인 생성의 주요 원인 중 하나가 바로 이 에너지를 줄이기 위함이다.
'''''E_λ''''' ('''자왜 이방성 에너지'''): 자화될 때 결정의 치수가 약간 변하는 자왜 효과 때문에 발생하는 에너지다. 결정 격자에 탄성 변형을 일으키며, 이 변형 에너지를 최소화하는 자화 방향이 선호된다. 이 에너지는 결정 내 도메인들의 자화 축이 모두 평행할 때 최소화되는 경향을 보인다.
'''''E_k''''' ('''결정 자기 이방성 에너지'''): 자기 이방성으로 인해 결정 격자는 특정 방향으로 자화되기 쉽고, 다른 방향으로는 어렵다. 이 에너지는 자화가 "쉬운" 결정 축을 따를 때 최소화된다. 따라서 결정 입자 내 대부분의 도메인 자화는 "쉬운" 축을 따라 양방향으로 향한다. 재료 내 개별 입자들의 결정 격자는 서로 다른 무작위 방향으로 정렬되는 경우가 많아, 입자마다 지배적인 도메인 자화 방향이 달라진다.
'''''E_H''''' ('''제만 에너지'''): 자기 재료와 외부 자기장 간의 상호작용으로 인해 자기 정전 에너지에 더해지거나 빠지는 에너지다. 자기장과 자화 벡터 사이 각도의 코사인의 음수에 비례한다. 자기장과 평행하게 정렬된 도메인은 이 에너지를 감소시키고, 반대 방향으로 정렬된 도메인은 증가시킨다. 강자성 재료에 자기장을 가하면 도메인 벽이 이동하여 자기장과 평행한 도메인이 커지고, 반대 방향 도메인은 작아진다. 이것이 강자성 재료가 "자화"되는 과정이다. 충분히 강한 외부 자기장이 가해지면 반대 방향 도메인은 소멸하는데, 이를 포화라고 한다.

일부 문헌에서는 벽 에너지 ''E_W''를 교환 에너지 ''E_ex''와 결정 자기 이방성 에너지 ''E_k''의 합으로 정의하기도 한다.

안정적인 도메인 구조는 재료 전체에서 총 에너지 ''E''를 최소화하는 연속적인 벡터장 '''''M'''''('''''x''''') (자화 함수)로 나타낼 수 있다. 이 최소값을 찾기 위해 변분법을 사용하면 비선형 미분 방정식 집합(윌리엄 풀러 브라운 주니어의 이름을 따 ''브라운 방정식''이라 불림)이 유도된다. 원칙적으로 이 방정식을 풀어 안정적인 도메인 구성 '''''M'''''('''''x''''')를 구할 수 있지만, 실제로는 가장 간단한 경우만 풀 수 있다. 해석적 해는 존재하지 않으며, 유한 요소법으로 계산된 수치 해는 도메인과 벽 크기 차이가 커서 계산이 어렵다. 마이크로마그네틱스는 도메인 내부 쌍극자 자화가 벽에서 멀리 떨어진 곳에서는 모두 같은 방향을 가리킨다고 가정하는 근사 방법을 개발하여, 자화 변화가 빠른 도메인 벽 근처에서만 수치 해를 사용한다.

5. 자기 구역 관찰 기술

자기 재료 표면의 자화를 시각화하여 자기 도메인을 보여주는 데에는 여러 현미경 방법이 사용된다. 각 방법은 자기 재료의 도메인이 원형, 사각형, 불규칙, 길쭉한 모양, 줄무늬 등 다양한 크기와 치수를 가질 수 있기 때문에 서로 다른 응용 분야를 가진다.

커 현미경법: 25~100 마이크로미터 범위의 큰 자구를 관찰할 수 있다.
로렌츠 현미경: 나노 규모의 자기 도메인 구조를 연구하는 데 사용되는 투과 전자 현미경 기술이다.^[9]
자기력 현미경: 수 나노미터 크기까지의 미세한 자구 구조를 관찰하는 데 사용된다.
비터 패턴: 프랜시스 비터가 처음 관찰한 자기 도메인 이미지화 기술이다.^[10]

5. 1. 자기 광학 커 효과 (Magneto-optic Kerr effect, MOKE)

커 현미경법은 자화된 표면에서 반사된 빛의 편광이 회전하는 자기 광학 커 효과를 이용하여 25~100 마이크로미터 범위의 큰 자구를 쉽게 관찰할 수 있게 해준다.^[1]

5. 2. 로렌츠 현미경 (Lorentz microscopy)

로렌츠 현미경은 나노 규모까지 자기 도메인 구조를 연구하는 데 사용되는 투과 전자 현미경 기술이다.^[9] 가장 일반적인 기술로는 병렬 빔 TEM 모드에서 프레넬 모드, 푸코 모드 및 저각 전자 회절(LAD)과 주사형 TEM 모드에서 차등 위상 대비(DPC)가 있다. 오프 축 전자 홀로그래피는 나노 규모 자기장을 감지하여 자기 구조를 관찰하는 데 사용되는 관련 기술이다.

5. 3. 자기력 현미경 (Magnetic force microscopy, MFM)

자기력 현미경(MFM)은 수 나노미터 크기까지의 미세한 자구 구조를 관찰하는 기술이다. MFM은 자기적으로 코팅된 탐침 팁을 사용하여 표면을 스캔하는 형태의 원자 힘 현미경이다.^[1]

5. 4. 비터 방법 (Bitter method)

프랜시스 비터가 처음 관찰한 자기 도메인을 이미지화하는 기술이다.^[10] 이 기술은 강자성 유체 소량을 강자성 재료 표면에 놓는 것을 포함한다. 강자성 유체는 도메인 내에 위치한 재료 영역보다 높은 자기 선속을 갖는 자기 도메인 벽을 따라 정렬된다.

수정된 비터 기술은 널리 사용되는 장치인 대면적 도메인 뷰어에 통합되었으며, 특히 실리콘 강의 결정 배향을 검사하는 데 유용하다.^[11]

참조

_[1] 논문 La variation du ferromagnetisme du temperature 1906
_[2] 서적 Introduction to Magnetic Materials Wiley–IEEE
_[3] 서적 The Feynman Lectures on Physics, Vol. II https://books.google[...] California Inst. of Technology
_[4] 서적 Rock magnetism : fundamentals and frontiers Cambridge University Press 1997
_[5] 서적 Rock Magnetism: Fundamentals and Frontiers https://books.google[...] Cambridge University Press 2001-08-30
_[6] 학위논문 Dominios magnéticos y respuesta dinámica en aleaciones ferromagnéticas de FeP http://ricabib.cab.c[...] Universidad Nacional de Cuyo 2020-05-13
_[7] 서적 Micromagnetics and Recording Materials https://books.google[...] Springer Science & Business Media 2012-04-28
_[8] 서적 Magnetic domains and techniques for their observation The English University Press Ltd 1966
_[9] 서적 Magnetic Microscopy of Nanostructures Springer-Verlag
_[10] 문서 A Dictionary of Physics Oxford University Press 2009
_[11] 간행물 A Large area domain viewer Proceedings of SMM9 1989
_[12] 웹사이트 磁区 http://www.shinetsu-[...] 信越化学工業 2018-12-24

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com