층밀림 변형력

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 일반적인 전단 응력
- 2.1. 전단 응력 계산
3. 여러 형태의 전단 응력
4. 전단 응력 측정 센서
5. 토질역학에서의 전단 강도
6. 훅의 법칙 (フックの法則)
7. 공액 전단 응력 (共役剪断応力)
참조

1. 개요

층밀림 변형력은 단위 면적당 작용하는 힘인 전단 응력을 의미하며, 다양한 형태와 분야에서 나타난다. 평균 전단 응력은 힘과 단면적의 비율로 계산되며, 벽 전단 응력은 유체와 벽면 사이의 저항력을 나타내고, 순수 전단 응력은 전단 변형률과 관련된다. 또한, 보 휨 전단력, 세미 모노코크 구조, 토양 구조물, 충격, 유체 등 다양한 환경에서 발생하며, 각 경우에 따라 계산식이 달라진다. 전단 응력은 센서를 통해 측정될 수 있으며, 토질역학에서는 흙의 전단 강도를 결정하는 중요한 요소로 작용한다. 훅의 법칙은 전단 응력과 전단 변형률의 관계를 나타내며, 공액 전단 응력은 입방체에서 전단 응력의 평형 조건을 설명한다.

2. 일반적인 전단 응력

물체에 가해지는 힘과 단면적의 관계로 전단 응력을 정의할 수 있다. 평균 전단 응력 τ^영어는 가해지는 힘 F^영어를 힘과 평행한 단면적 A^영어로 나눈 값이다.^[1]

2. 1. 전단 응력 계산

평균 층밀림 변형력 τ 또는 단위 면적당 힘을 계산하는 공식은 다음과 같다.^[15]

:τ = F / A

여기서,

''F''는 적용된 힘이다.
''A''는 단면적이다.

관련된 영역은 적용된 힘 벡터에 평행한 재료 면, 즉 힘에 수직인 표면 법선 벡터에 해당한다.^[1]

3. 여러 형태의 전단 응력

여러 형태의 전단 응력은 다양한 상황에서 발생하며, 각각 다른 특징을 가진다.

벽 전단 응력: 벽면에 인접하여 흐르는 유체 층에서 벽면으로부터의 저항력(단위 면적당)을 나타낸다.
순수 전단 응력: 순수 전단 변형률과 관련이 있으며, 등방성 재료의 전단 탄성 계수와 영률, 푸아송 비를 통해 계산할 수 있다.
보 전단: 보에 가해지는 전단력에 의해 발생하는 보의 내부 전단 응력으로, 드미트리 이바노비치 주라프스키의 이름을 따서 주라프스키 전단 응력 공식이라고도 한다.
세미 모노코크 전단: 세미 모노코크 구조 내의 전단 응력은 구조의 단면을 스트링거와 웹으로 이상화하여 계산할 수 있다.
충격 전단: 고체 원형 막대에 충격이 가해질 때 발생하는 최대 전단 응력을 나타낸다.
유체에서의 전단 응력: 실제 유체(액체 및 기체 포함)가 고체 경계를 따라 이동할 때 경계에서 발생하는 전단 응력이다. 뉴턴 유체와 비뉴턴 유체에 따라 다르게 정의된다. 점착 조건^[7]은 경계에서의 유체 속도가 0임을 나타낸다.

3. 1. 벽 전단 응력 (Wall shear stress)

벽 전단 응력은 벽면에 인접하여 흐르는 유체 층에서 벽면으로부터의 저항력(단위 면적당)을 나타낸다. 다음과 같이 정의된다.

:

\tau_w := \mu\left.\frac{\partial u}{\partial y}\right|_{y=0},

여기서 μ는 동점성 계수, u는 유속, y는 벽면으로부터의 거리이다.

예를 들어, 동맥 혈류의 설명에 사용되며, 여기서 벽 전단 응력이 죽상 동맥 경화증 과정에 영향을 미친다는 증거가 있다.^[2]

3. 2. 순수 전단 응력 (Pure shear stress)

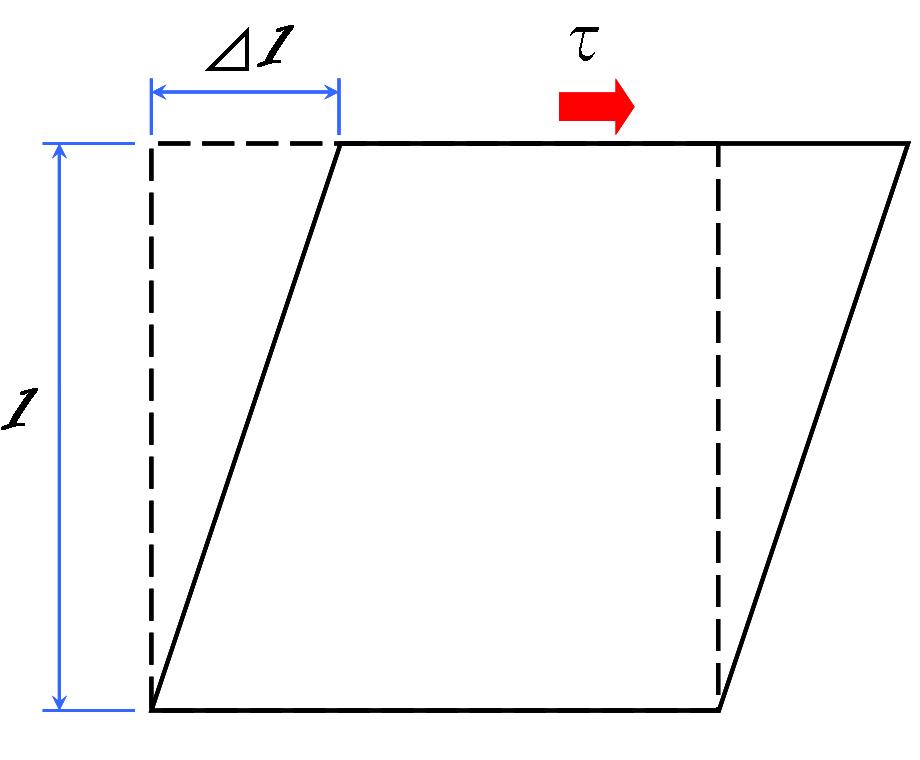
전단 응력이 작용하는 물체는 그림 1과 같이 평행사변형으로 변형되어 전단 변형률

:γ|감마^영어 = Δl / l

이 발생한다. 전단 탄성 계수를 G라고 하면, 전단 응력과 전단 변형률의 관계는 훅의 법칙에 의해 다음 식으로 나타낸다.

:γ|감마^영어 = τ|타우^영어 / G

3. 3. 보 전단 (Beam shear)

보 휨 전단력은 보에 가해지는 전단력에 의해 발생하는 보의 내부 전단 응력으로 정의된다.

:

\tau := \frac{fQ}{Ib},

$f$ 는 해당 위치의 총 전단력
$Q$ 는 도심 모멘트
$b$ 는 전단에 수직인 재료의 두께(폭)
$I$ 는 전체 단면적의 관성 모멘트

보 휨 전단력 공식은 1855년에 이를 유도한 드미트리 이바노비치 주라프스키의 이름을 따서 주라프스키 전단 응력 공식이라고도 한다.^[1]

3. 4. 세미 모노코크 전단 (Semi-monocoque shear)

세미 모노코크 구조에서 전단 응력은 구조 단면을 스트링거(축 방향 하중만 담당)와 웹(전단 흐름만 담당)으로 이상화하여 계산할 수 있다. 전단 응력을 구하려면 전단 흐름을 세미 모노코크 구조 해당 부분의 두께로 나누면 된다. 따라서 최대 전단 응력은 최대 전단 흐름이 발생하거나 두께가 가장 얇은 웹에서 발생한다.^[1]

토양 구조물도 전단 때문에 파괴될 수 있다. 예를 들어 흙으로 채운 댐이나 제방의 무게 때문에 작은 산사태처럼 지반이 무너질 수 있다.^[1]

3. 5. 충격 전단 (Impact shear)

고체 원형 막대에 충격이 가해질 때 발생하는 최대 전단 응력은 다음 식으로 나타낼 수 있다.^[6]

식	$\tau = 2\sqrt {\frac{UG}{V}}$
변수	설명
U	운동 에너지의 변화량
G	전단 탄성 계수
V	막대의 부피

또한,

''U'' = ''U''_회전 + ''U''_가해짐

식	설명
U_회전	$U_{회전} = \frac{1}{2} I \omega^2$
U_가해짐	U_가해짐 = Tθ_변위
I	질량 관성 모멘트
ω	각속도

3. 6. 유체에서의 전단 응력 (Shear stress in fluids)

뉴턴 유체는 비압축성 유동, 등방성 조건에서 다음과 같은 간단한 식으로 나타낼 수 있다.^[2]

:

\tau = \mu {du \over dx}

여기서,

:*

\tau

는 유체에 작용하는 층밀림 변형력(shear stress)

:*

\mu

는 유체의 점성계수

:*

{du \over dx}

는 층밀림 힘(shear force)에 수직한 방향의 속도 기울기로 표현되는 전단변형률이다.

'''벽 전단 응력'''은 벽면에 인접하여 흐르는 유체 층에서 벽면으로부터의 저항력(단위 면적당)을 나타낸다. 모든 실제 유체(액체 및 기체 포함)가 고체 경계를 따라 이동하면 해당 경계에서 전단 응력이 발생한다. 점착 조건^[7]은 경계에서의 유체 속도(경계에 상대적)가 0임을 나타낸다. 경계에서 어느 정도 높이에서 흐름 속도는 유체의 속도와 같아야 한다. 이 두 지점 사이의 영역을 경계층이라고 한다.

층류의 모든 뉴턴 유체에 대해 전단 응력은 유체의 변형률에 비례하며, 점성은 비례 상수이다. 비뉴턴 유체의 경우 점성은 일정하지 않다. 전단 응력은 이러한 속도 손실의 결과로 경계에 가해진다. 유속의 함수로서의 전단 응력이 주어지면, 이는 유속의 기울기에 대한 상수로 표현될 수 있는 경우에만 뉴턴 흐름을 나타낸다. 이 경우 얻는 상수는 흐름의 동점성 계수이다.

3. 6. 1. 유체 전단 응력 예시

뉴턴 유체의 경우, 특정 지점에서 평판과 평행한 표면 요소에 작용하는 전단 응력은 다음과 같이 표현된다.^[7]

:

여기서

는 흐름의 동점성 계수를 나타낸다.
는 경계를 따라 흐르는 유속을 의미한다.
는 경계로부터의 높이를 나타낸다.

특히, 벽면에서의 전단 응력은 다음과 같이 정의된다.

:

일반적인 기하학적 구조에서 뉴턴 점성 법칙에 따르면, 전단 텐서(2차 텐서)는 유속 기울기에 비례한다.^[7]

:

이때 비례 상수는 ''동점성 계수''라고 불린다. 등방성 뉴턴 흐름의 경우 이 값은 스칼라이며, 비등방성 뉴턴 흐름의 경우에는 2차 텐서가 될 수 있다. 뉴턴 유체의 핵심 특징은 동점성 계수가 유속에 독립적이라는 점이다(즉, 전단 응력 구성 법칙이 ''선형''이다). 반면, 비뉴턴 흐름에서는 이러한 관계가 성립하지 않아, 다음과 같은 수정이 필요하다.

:

이는 더 이상 뉴턴의 법칙이 아닌 일반적인 텐서 항등식으로 간주된다.

데카르트 좌표계에서 2차원 공간을 고려할 때 (유속 성분은 각각 ), 전단 응력 행렬은 다음과 같이 나타낼 수 있다.

:

이는 뉴턴 유동을 나타낸다.

점성 텐서가 다음과 같이 표현되는 비등방성 유동의 경우,

:

이 점성 텐서는 공간 좌표에 따라 변하며(균일하지 않음) 시간에 따라 변하지만(과도적), 유속에는 독립적이다. 따라서 이 유동은 뉴턴 유동으로 분류된다.

반면, 점성이 다음과 같이 표현되는 유동은

:

점성이 유속에 의존하므로 비뉴턴 유동에 해당한다. 이 비뉴턴 유동은 등방성을 가지므로(행렬이 단위 행렬에 비례), 점성은 단순한 스칼라 값으로 나타낼 수 있다.

:

4. 전단 응력 측정 센서

벽면 전단 응력을 측정하는 방법에는 여러 가지가 있다. 센서를 이용하여 벽면에서의 속도 구배를 직접 측정하고, 여기에 동점성 계수를 곱하여 전단 응력을 얻는 방법이 있다. A. A. 나크위와 W. C. 레이놀즈는 이 방법을 시연하였다.^[8]

최근에는 마이크로 광학 제작 기술이 발전하면서 통합 회절 광학 소자를 이용한 발산 프린지 전단 응력 센서가 개발되어 공기와 액체 모두에서 측정이 가능해졌다.^[9]

이 외에도 유연한 폴리디메틸실록산 중합체로 만들어진 마이크로 기둥을 이용하는 방법,^[10]^[11] 전기 확산법을 이용하는 방법^[12] 등이 있다.

4. 1. 발산 프린지 전단 응력 센서 (Diverging fringe shear stress sensor)

벽면 전단 응력 측정에는 이 관계가 활용될 수 있다. 센서가 벽면에서의 속도 기울기를 직접 측정할 수 있다면, 동점성 계수를 곱하여 전단 응력을 얻을 수 있다. 이러한 센서는 A. A. 나크위(A. A. Naqwi)와 W. C. 레이놀즈(W. C. Reynolds)가 시연하였다.^[8] 두 평행 슬릿을 통과하는 빛의 광선으로 생성된 간섭 패턴은, 두 슬릿 평면에서 시작되는 것처럼 보이는 선형적으로 발산하는 프린지 네트워크를 형성한다 (이중 슬릿 실험 참조). 유체 내 입자가 프린지를 통과할 때, 수신기는 프린지 패턴의 반사를 감지한다. 신호 처리를 통해 프린지 각도로부터 입자의 높이와 속도를 추정(외삽)할 수 있다. 측정된 벽면 속도 기울기 값은 유체 특성과 무관하여 보정이 필요하지 않다. 최근 마이크로 광학 제작 기술 발전으로, 통합 회절 광학 소자를 사용해 공기와 액체 모두에서 사용 가능한 발산 프린지 전단 응력 센서 제작이 가능해졌다.^[9]

4. 2. 마이크로 기둥 전단 응력 센서 (Micro-pillar shear-stress sensor)

마이크로 기둥 전단 응력 센서는 유연한 폴리디메틸실록산 중합체로 만들어진, 벽에 부착된 가늘고 작은 기둥을 이용한다. 이 마이크로 기둥은 벽 근처에서 가해지는 항력에 반응하여 구부러진다. 따라서 이 센서는 벽면 근처의 속도 기울기와 국부적인 벽면 전단 응력 사이의 관계에 의존하는 간접 측정 원리를 따른다.^[10]^[11]

4. 3. 전기 확산 방식 (Electro-diffusional method)

전기 확산법은 제한 확산 전류 조건에서 미세 전극으로부터 액상에서의 벽 전단율을 측정한다. 넓은 표면의 양극(보통 측정 영역에서 멀리 떨어진 곳에 위치)과 음극 역할을 하는 작은 작동 전극 간의 전위차는 빠른 산화 환원 반응을 유발한다. 이온 소실은 미세 탐침 활성 표면에서만 발생하여 확산 경계층이 발달하며, 여기서 빠른 전기 확산 반응 속도는 확산에 의해서만 제어된다. 미세 전극의 벽 근처 영역에서 대류-확산 방정식의 해는 미세 탐침의 특성 길이, 전기 화학 용액의 확산 특성 및 벽 전단율에 의존하는 해석적 해로 이어진다.^[12]

5. 토질역학에서의 전단 강도

흙이 전단 응력을 받아 뚜렷한 전단 변형이나 명확한 전단 활동을 일으키면 '흙이 전단 파괴되었다'고 하며, 이때 활동면 상의 전단 응력을 전단 강도(shear strength)라고 한다. 전단강도는 흙의 종류뿐만 아니라 같은 흙에서도 다르게 나타날 수 있다.^[1]

흙으로 채워진 댐이나 제방의 무게 때문에 작은 산사태처럼 지반이 붕괴되는 등, 토양 구조물도 전단으로 인해 파괴될 수 있다.

5. 1. Mohr-Coulomb 파괴 규준

흙이 전단 응력을 받아 뚜렷한 전단 변형을 일으키거나 명확한 전단 활동을 일으킨다면, 이를 '흙이 전단 파괴되었다'고 하며, 이때 활동면 상의 전단 응력을 전단 강도(shear strength)라고 한다. 모어-쿨롬(Mohr-Coulomb)의 이론에 따르면 전단강도는 흙 입자 사이에 작용하는 점착력(c)과 마찰에 의해 결정된다. Φ는 내부마찰각 또는 전단저항각이라고 한다.^[1] 흙의 전단 강도 식은 다음과 같다.^[2]

:τ = c + σ tanΦ

여기서 σ는 전응력을 나타낸다. 만약 공극 수압이 발생한다면, 위 식에서 전응력이 아닌 유효응력을 대입하여 계산해야 한다. 즉,

:τ = c + σ̅ tanΦ

유효응력이란 전응력에서 공극 수압을 뺀 것과 같다 (σ̅ = σ - u).

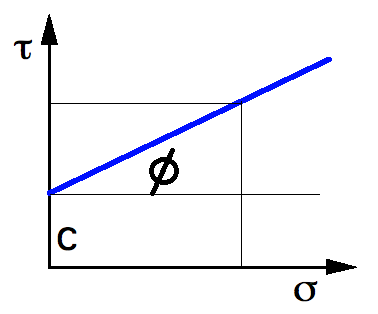
σ와 τ에 따른 파괴 포락선(failure envelope)은 실제로 곡선이지만, 계산의 편의 상 직선으로 보고 사용하며, 이를 '''모어―쿨롬의 파괴규준'''(Mohr―Coulomb failure criteria)이라고 한다. 파괴 규준 선 이하에 σ, τ가 위치하면 아직 전단파괴가 일어나지 않은 것이고, 파괴 규준 선에 점이 위치하면 전단파괴가 일어난 것을 의미한다.^[3]

전단강도는 흙의 종류에 따라 달라지는 것이 아니라 같은 흙이라도 다르게 나타날 수 있다.^[4]

'''전단강도에 영향을 주는 현장 요인들'''^[5]

공극비, 입도, 흙 입자 형상
함수비
하중 재하 속도. 급속 하중 재하는 과잉간극수압을 발생시킴
강도의 비등방성: 연직방향과 수평방향의 강도가 다를 수 있음.

'''전단강도에 영향을 주는 실내 실험 요인들'''^[6]

과잉간극수압 발생 여부
시료 교란 여부
함수비

5. 2. 전단 강도에 영향을 미치는 요인

흙의 전단 강도에 영향을 미치는 요인은 현장 조건과 실내 실험 조건에 따라 달라진다.^[1]
현장 요인^[1]

공극비, 입도, 흙 입자 형상
함수비
하중 재하 속도: 급속 하중 재하는 과잉간극수압을 발생시킨다.
강도의 비등방성: 연직 방향과 수평 방향의 강도가 다를 수 있다.

실내 실험 요인^[1]

과잉간극수압 발생 여부
시료 교란 여부
함수비

이러한 요인들은 한국의 지반 특성 및 지반 조사 시에도 중요하게 고려해야 한다. 예를 들어, 한국은 산지가 많고 다양한 지질 조건을 가지므로, 지반 조사 시 흙의 공극비, 입도, 함수비 등을 면밀히 파악하여 전단 강도를 정확하게 평가해야 한다. 또한, 강우량이 많은 여름철에는 함수비 변화에 따른 지반 강도 변화를, 지진 발생 시에는 하중 재하 속도 및 과잉간극수압 발생 여부를 주의 깊게 고려해야 한다.

5. 3. Mohr의 응력원

지표면에서 z 거리만큼 아래에 있는 흙의 미소 단위에 대해 생각해보자. 이 미소 요소에 수직으로 작용하는 응력을 $$\sigma_1$$, 수평으로 작용하는 응력을 $$\sigma_3$$라 할 때, 미소 요소 내의 임의 경사면 상에서의 수직 응력과 전단 응력을 구할 수 있다. $$\sigma_1>\sigma_3$$라고 가정한다면, $$\sigma_1$$이 작용하는 면을 최대 주응력면이라고 하고, $$\sigma_3$$가 작용하는 면을 최소 주응력면이라고 한다. 이때 $$\theta$$는 최대 주응력면과 응력을 구하려는 면이 이루는 각이다.^[1] 해당 경사면에 작용하는 수직 응력과 전단 응력은 다음과 같다.

$$\sigma=\frac{\sigma_1+\sigma_3}{2}+\frac{\sigma_1-\sigma_3}{2}cos 2\theta$$

$$\tau=\frac{\sigma_1-\sigma_3}{2}sin 2\theta$$

$$\theta = 45^\circ + \frac{\phi}{2}$$

6. 훅의 법칙 (フックの法則)

순수 전단 응력은 순수 전단 변형률과 관련이 있으며, $\gamma$ 로 표시되고, 다음 방정식에 의해 표현된다.^[3]

: $\tau = \gamma G,$

여기서 $G$ 는 등방성 재료의 전단 탄성 계수이며, 다음과 같이 주어진다.

: $G = \frac{E}{2(1+\nu)}.$

여기서, $E$ 는 영률이고, $\nu$ 는 푸아송 비이다.

전단 응력이 작용하는 물체는 그림 1과 같이 평행 사변형으로 변형되어 전단 변형률

: $\gamma = \mathit{\Delta}l/ l$

이 발생한다. 전단 탄성 계수를 $G$ 라고 하면, 전단 응력과 전단 변형률의 관계는 훅의 법칙에 의해 다음 식으로 나타낸다.

: $\gamma= \frac{\tau}{G}$

7. 공액 전단 응력 (共役剪断応力)

x

축과

y

축을 법선으로 하는 면으로 구성된 입방체를 자유 물체로 고체에서 떼어낸 경우를 생각한다.

이때,

y

축을 법선으로 하는 면의

X

방향으로 작용하는 전단 응력을

\tau_{xy}

라고 하면, 병진·회전에 관한 평형 조건으로부터 입방체에는

\tau_{yx}

도 작용해야 하며, 또한

\tau_{yx} = \tau_{xy}

의 관계가 성립한다(그림 2). 이것을 공액 전단 응력이라고 한다. 전단 응력은 이러한 상태에서만 성립한다는 점에 주의해야 한다.

참조

_[1] 서적 Mechanics of Materials Pearson Education
_[2] 간행물 Wall Shear Stress: Theoretical Considerations and Methods of Measurement
_[3] 웹사이트 Strength of Materials http://www.eformulae[...] 2011-12-24
_[4] 웹사이트 http://sopromato.ru/[...] 2014-02-26
_[5] 웹사이트 Flexure of Beams http://www.eng.mcmas[...] McMaster University
_[6] 웹사이트 Shear Stress Equations and Applications https://engineersedg[...] 2024-08-29
_[7] 간행물 The no-slip condition of fluid dynamics https://doi.org/10.1[...] Springer Netherlands
_[8] 간행물 Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow 1987-01
_[9] 문서 "{microS Shear Stress Sensor, MSE}"
_[10] 간행물 Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars
_[11] 간행물 Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³
_[12] 간행물 A revisit of the electro-diffusional theory for the wall shear stress measurement https://hal.archives[...]
_[13] 웹사이트 オンライン学術用語集検索ページ http://dbr.nii.ac.jp[...] 文部科学省・国立情報学研究所 2015-12-05
_[14] 웹사이트 한국물리학회 물리학용어집 https://www.kps.or.k[...]
_[15] 서적 Mechanics of Materials Pearson Education

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com