탄성률

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 선형 및 비선형
- 3.1. 선형 탄성
- 3.2. 비선형 탄성
4. 등방성 및 비등방성
- 4.1. 등방성 재료
- 4.2. 비등방성 재료
5. 탄성 계수의 종류
6. 탄성 계수의 관계식
7. 탄성 계수 계산
8. 복소 탄성 계수
참조

1. 개요

탄성률은 물체의 탄성 변형 영역에서 응력과 변형률의 비율로 정의되며, 재료의 강성을 나타내는 중요한 지표이다. 탄성률은 선형, 비선형, 등방성, 비등방성 등 다양한 형태로 나타나며, 영률, 전단 탄성 계수, 체적 탄성 계수, 굽힘 탄성 계수 등 여러 종류가 있다. 재료의 탄성 계수는 밀도 범함수 이론(DFT)을 이용한 계산을 통해 얻을 수 있으며, 복소 탄성률을 통해 점탄성 거동을 설명할 수 있다.

더 읽어볼만한 페이지

성능 - 변형력-변형 곡선
변형력-변형 곡선은 재료의 응력과 변형률 관계를 그래프로 나타내어 탄성 계수, 항복 강도, 인장 강도, 연성, 인성 등 기계적 특성을 파악하고, 재료 종류에 따라 다른 형태를 가지며 선형 탄성 영역, 소성 변형 영역, 가공 경화 영역, 네킹 영역 등을 포함하는, 구조물 안전성 평가 및 재료 선택에 중요한 도구이다.
성능 - 응답 시간
응답 시간은 시스템이 서비스 요청에 응답하는 데 소요되는 시간으로, 자료 처리, 실시간 시스템, 디스플레이 등 다양한 분야에서 시스템의 응답성을 나타내는 중요한 지표이며, 컴퓨팅 환경에서는 서비스 시간과 대기 시간의 합으로, 네트워크 환경에서는 전송 시간까지 포함된다.
변형 - 소성 (물리학)
소성(塑性)은 물리학에서 외부 응력에 의해 재료가 영구적으로 변형되는 현상이며, 금속, 결정성 및 비정질 재료, 세포 재료 등 다양한 물질에서 발생하고 변형 이론과 흐름 소성 이론으로 설명된다.
변형 - 변형력-변형 곡선
변형력-변형 곡선은 재료의 응력과 변형률 관계를 그래프로 나타내어 탄성 계수, 항복 강도, 인장 강도, 연성, 인성 등 기계적 특성을 파악하고, 재료 종류에 따라 다른 형태를 가지며 선형 탄성 영역, 소성 변형 영역, 가공 경화 영역, 네킹 영역 등을 포함하는, 구조물 안전성 평가 및 재료 선택에 중요한 도구이다.
재료역학 - 비등방성
비등방성은 재료의 미세구조, 결정구조, 분자 배열 등으로 인해 물질의 물리적, 화학적 성질이 방향에 따라 달라지는 현상으로, 다양한 분야에서 중요한 역할을 하며 측정 및 분석을 통해 재료 설계 및 응용에 활용된다.
재료역학 - 비틀림
비틀림은 물체에 동일하고 반대 방향의 힘이 작용하여 꼬이는 현상으로, 구조 부재에 비틀림 모멘트가 작용할 때 발생하며, 전단 응력을 유발하고, 비틀림 상수, 전단 응력, 비틀림 각도 등으로 분석되며 샤프트 설계에 중요하다.

탄성률
일반 정보
정의	재료의 강성을 측정하는 물리적 특성
영어 명칭	Elastic modulus
다른 영어 명칭	Modulus of elasticity

2. 정의

물체의 탄성 계수는 탄성 변형 영역에서 응력-변형률 곡선의 기울기로 정의된다.^[1] 더 단단한 재료는 더 높은 탄성 계수를 가진다. 탄성 계수는 다음과 같은 형태를 갖는다.

: $\delta \ \stackrel{\text{def}}{=}\ \frac {\text{응력}} {\text{변형률}}$

여기서 응력은 변형을 일으키는 힘을 힘이 가해지는 면적으로 나눈 값이고, 변형률은 변형으로 인해 발생하는 어떤 매개변수의 변화와 매개변수의 원래 값의 비율이다.

변형률은 무차원량이므로 $\delta$ 의 단위는 응력의 단위와 같다.^[2] 탄성 계수는 가해진 응력에 대한 재료의 강성을 정량화하는 특정 매개변수이며, 재료의 탄성 특성을 정의하는 데 기본이 된다. 이러한 계수는 이방성 재료에서 선형 방정식을 통해 응력과 변형률을 관련시키는 텐서 표기법의 강성 행렬의 요소를 형성한다. 일반적으로 ''C_ijkl''로 표시되며, 여기서 ''i'', ''j'', ''k'', 및 ''l''은 좌표 방향을 나타내며, 이러한 계수는 다양한 하중에서 재료가 어떻게 변형되는지 이해하는 데 필수적이다.^[3]

3. 선형 및 비선형

많은 재료는 일정 구간의 변형도에 대해 상수의 탄성 계수를 갖는다. 이런 종류의 재료를 '''선형''' 재료라고 하며, 훅 법칙을 따른다. 강, 탄소 섬유, 유리 등이 이에 속한다. 고무나 (아주 작은 변형도를 벗어나는) 흙은 '''비선형''' 재료이다.

3. 1. 선형 탄성

많은 재료는 일정 구간의 변형도에 대해 상수의 탄성 계수를 갖는다. 이런 종류의 재료를 '''선형''' 재료라고 하며, 훅 법칙을 따른다고 한다. 이런 재료에는 강, 탄소 섬유와 유리 등이 있다. 고무나 (아주 작은 변형도를 벗어나는) 흙은 '''비선형''' 재료이다.

3. 2. 비선형 탄성

많은 재료는 일정 구간의 변형도에 대해 상수의 탄성 계수를 갖는다. 이런 종류의 재료를 '''선형''' 재료라고 하며, 훅 법칙을 따른다고 한다. 이런 재료에는 강, 탄소 섬유와 유리 등이 있다. 고무나 (아주 작은 변형도를 벗어나는) 흙은 '''비선형''' 재료이다.

4. 등방성 및 비등방성

비등방성 재료는 하중이 작용하는 방향에 따라 탄성 계수의 값이 다르다. 탄소 섬유, 목재, 철근 콘크리트 등이 이에 해당한다.^[3] 탄성 계수는 응력에 대한 재료의 강성을 나타내는 값으로, 재료의 탄성 특성을 정의하는 기본 요소이다.

등방성 및 비등방성 물질의 특성과 등방 균질 탄성체의 탄성률 간 변환식은 '등방성 재료' 및 '비등방성 재료' 하위 섹션을 참조하라.

4. 1. 등방성 재료

일반적으로 등방성 물질(무정형 폴리머, 비정질·무배향 폴리머 등)의 경우 3가지 탄성률(인장 탄성률

E

, 전단 탄성률

G

, 체적 탄성률

K

) 간의 관계는 다음과 같다.^[14]

:

E = 2G(1 - \nu) = 3K(1 - 2\nu)

여기서

\nu

는 종방향 변형률과 횡방향 변형률의 비(푸아송 비)이다. 결정성 폴리머, 섬유, 필름, 섬유 충전 복합 재료, 일반 사출 성형품 등은 등방성 물질이 아니다. 고분자 사슬, 충전 섬유, 결정상 등에 배향성을 가지며, 그 정도는 내부와 표면에서 다르다. 이러한 이방성 물질은 2개 이상의 독립된 탄성률을 갖는다.^[15]

재료가 등방 균질 탄성 재료라고 가정하면, 탄성률 텐서 '''''D'''''의 독립 성분은 2개로 제한되고,^[12] 다음 식으로 쓸 수 있다.^[13]

:

D_{ijkl}=\lambda\delta_{ij}\delta_{kl}+G(\delta_{ik}\delta_{jl}+\delta_{il}\delta{jk})

여기서 δ는 크로네커 델타이다.

이 경우, 영률 ''E'', 푸아송 비 ν, 체적 탄성률 ''K'', 강성률 ''G'', 라메의 제1상수 λ의 5개의 탄성률은 각각 2개를 사용하여 나머지 3개를 나타낼 수 있다. 그 관계는 아래 표와 같다.

등방 균질 탄성체의 각 탄성률 간의 변환식
	$E$ （영률）	$\nu$ （푸아송 비）	$K$ （체적 탄성률）	$G$ （강성률）	$\lambda$ （라메의 제1상수）
$E, \nu$	$E$	$\nu$	$\dfrac{E}{3(1-2\nu)}$	$\dfrac{E}{2(1+\nu)}$	$\dfrac{E\nu}{(1+\nu)(1-2\nu)}$
$E, K$	$E$	$\dfrac{3K-E}{6K}$	$K$	$\dfrac{3K E}{9K-E}$	$\dfrac{3K(3K-E)}{9K-E}$
$E, G$	$E$	$\dfrac{E-2G}{2G}$	$\dfrac{G E}{3(3G-E)}$	$G$	$\dfrac{G(E-2G)}{3G-E}$
$E, \lambda$	$E$	$\dfrac{2\lambda}{E+\lambda+\alpha}$	$\dfrac{E+3\lambda+\alpha}{6}$	$\dfrac{E-3\lambda+\alpha}{4}$	$\lambda$
$\nu, K$	$3K(1-2\nu)$	$\nu$	$K$	$\dfrac{3K(1-2\nu)}{2(1+\nu)}$	$\dfrac{3K\nu}{1+\nu}$
$\nu, G$	$2G(1+\nu)$	$\nu$	$\dfrac{2G(1+\nu)}{3(1-2\nu)}$	$G$	$\dfrac{2G\nu}{1-2\nu}$
$\nu, \lambda$	$\dfrac{\lambda(1+\nu)(1-2\nu)}{\nu}$	$\nu$	$\dfrac{\lambda(1+\nu)}{3\nu}$	$\dfrac{\lambda(1-2\nu)}{2\nu}$	$\lambda$
$K, G$	$\dfrac{9KG}{3K+G}$	$\dfrac{3K-2G}{6K+2G}$	$K$	$G$	$K-\frac{2}{3}G$
$K, \lambda$	$\dfrac{9(K-\lambda)}{3K-\lambda}$	$\dfrac{\lambda}{3K-\lambda}$	$K$	$\frac{3}{2}(K-\lambda)$	$\lambda$
$G, \lambda$	$\dfrac{G(3\lambda+2G)}{\lambda+G}$	$\dfrac{\lambda}{2\lambda+2G}$	$\dfrac{3\lambda+2G}{3}$	$G$	$\lambda$

4. 2. 비등방성 재료

비등방성 재료는 하중이 작용하는 방향에 따라 탄성 계수의 값이 다르다. 탄소 섬유, 목재, 철근 콘크리트 등이 비등방성 재료에 해당한다. 결정성 폴리머, 섬유, 필름, 섬유 충전 복합 재료, 일반 사출 성형품 등은 등방성 물질이 아니다. 이러한 재료들은 고분자 사슬, 충전 섬유, 결정상 등에 배향성을 가지며, 그 정도는 내부와 표면에서 다르다. 따라서 이방성 물질은 2개 이상의 독립된 탄성률을 갖는다.^[15]

재료가 등방 균질 탄성 재료라고 가정하면, 탄성률 텐서 '''''D'''''의 독립 성분은 2개로 제한된다.^[12]

5. 탄성 계수의 종류

탄성률은 탄성 변형에서의 응력과 변형률 사이의 비례 상수(응력/변형률)이며, 가해진 외력(응력)을 분자, 응력에 의해 유발된 변형률을 분모로 한 값이다.^[14] 탄성 변형은 늘어나거나 줄어드는 변형, 층밀리기 변형, 부피 변형의 세 가지 종류로 나뉘며, 탄성률도 세 종류가 있다.

물체의 탄성 계수는 탄성 변형 영역에서 응력-변형률 곡선의 기울기로 정의된다.^[1] 더 단단한 재료는 더 높은 탄성 계수를 갖는다. 변형률은 무차원량이므로 탄성률의 단위는 응력의 단위와 같다.^[2]

탄성률과 변형률을 측정하는 방법을 지정하면 방향을 포함하여 다양한 유형의 탄성률을 정의할 수 있다. 주요 탄성률 4가지는 다음과 같다.

종류	식	설명	그림
영률	$E = \frac{\sigma}{\varepsilon}$	인장력이나 압축력 등의 단축 응력에 대한 탄성률.	--
전단 탄성 계수	$G = \frac{\sigma}{\gamma}$	전단력에 대한 탄성률. 강성률이라고도 한다.	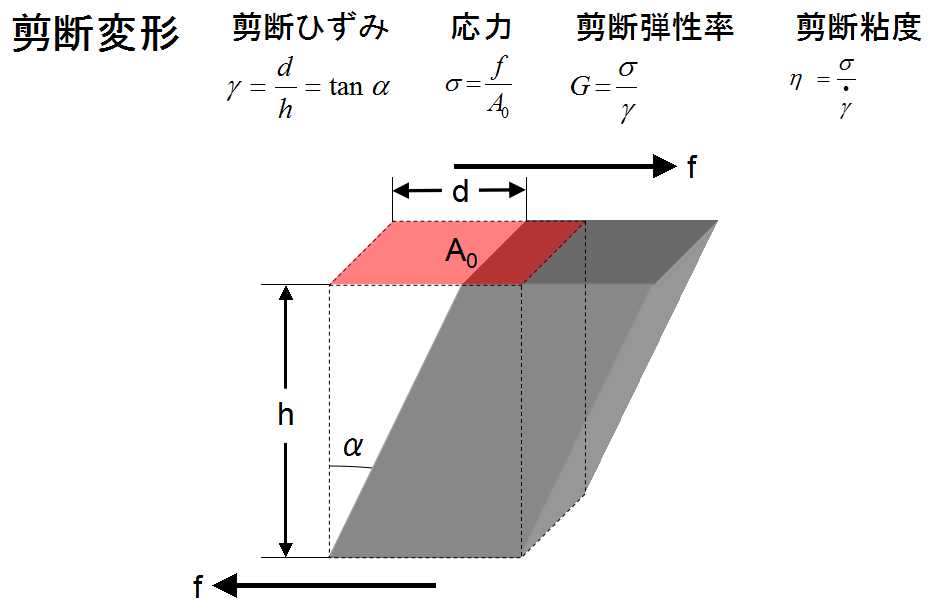단순한 전단 변형 모델. d는 변위, h는 힘과 수직인 두께, α는 기울어진 각도, γ는 전단 변형률, f는 힘, A_0는 변형 전 힘과 평행한 단면적, σ는 응력, G는 전단 탄성률, η는 전단 점도, 위에 점이 찍힌 γ는 전단 변형률의 시간 미분이다.
체적 탄성 계수	$K = \frac{\sigma}{\kappa}$	정수압 (직각 3방향의 힘)에 대한 탄성률. 압축성의 역수이며, 영률을 3차원으로 확장한 것이다.	--
굽힘 탄성 계수	E_flex	모멘트가 작용할 때 물체가 구부러지는 경향

'''영률''(E):' 단순히 ''탄성 계수''라고도 하며, 인장 및 압축 탄성을 설명한다.
'''전단 탄성 계수''(G):' 강성률이라고도 하며, 반대 방향의 힘이 작용할 때 물체가 층밀리기되는 경향을 설명한다.
'''체적 탄성 계수''(K):' 체적 탄성을 설명하며, 모든 방향에서 균일하게 하중이 가해질 때 물체가 모든 방향으로 변형되는 경향을 설명한다.
'''굽힘 탄성 계수''(''E''_flex): 모멘트가 작용할 때 물체가 구부러지는 경향을 설명한다.

그 외의 탄성 계수로는 라메의 첫 번째 매개변수 λ과 P파 탄성 계수 ''M''이 있다. 균질하고 등방성 (모든 방향에서 유사한) 물질(고체)은 두 개의 탄성 계수로 (선형) 탄성 특성이 완전히 설명되며, 어느 쌍이든 선택할 수 있다.

비점성 유체는 층밀리기 응력을 지지할 수 없다는 점에서 특수하며, 이는 층밀리기 탄성 계수가 항상 0임을 의미한다. 또한 이 그룹의 영률도 항상 0임을 의미한다.

일부 텍스트에서 탄성 계수는 ''탄성 상수''라고 하며, 그 역수를 ''탄성 계수''라고 한다.

5. 1. 인장 탄성 계수 (영률)

탄성 계수(E)는 인장 응력을 인장 변형도로 나누어 구할 수 있다.^[1]

:

E  = \frac{\sigma}{\varepsilon}= \frac{F/A_0}{\Delta l/l_0} = \frac{F l_0} {A_0 \Delta l}

탄성 계수 E의 단위는 파스칼이며, F는 작용하는 하중, A₀은 단면적,

\Delta l

는 재료의 길이 변화량, l₀은 재료의 원래 길이이다.

영률(E)은 인장 및 압축 탄성을 설명하며, 즉 반대 방향의 힘이 작용할 때 축을 따라 물체가 변형되는 경향을 설명한다. 영률은 인장 응력과 인장 변형률의 비율로 정의된다. 단순히 '탄성 계수'라고도 한다.

밀도 범함수 이론(DFT)은 재료의 기계적 응력에 대한 반응의 특징을 나타내는 여러 형태의 탄성 계수를 결정하는 신뢰할 수 있는 방법을 제공한다. VASP, 퀀텀 ESPRESSO, 또는 ABINIT와 같은 DFT 소프트웨어를 활용한다.

영률 (''E'') 계산 방법^[4]

1. 초기 구조: 재료의 이완된 구조로 시작한다. 모든 원자는 변형을 가하기 전에 최소 에너지 상태(즉, 원자에 작용하는 힘이 0인 최소 에너지 상태)에 있어야 한다.^[5]

2. 점진적 단축 변형: 특정 축을 따라 결정 구조에 작고 점진적인 변형을 적용한다. 이 변형은 일반적으로 단축 변형으로, 다른 차원은 일정하게 유지하거나 주기적으로 유지하면서 한 방향으로 격자를 늘리거나 압축한다.

3. 응력 계산: 각 변형된 구성에 대해 DFT 계산을 실행하여 결과 응력 텐서를 계산한다.

4. 응력-변형률 곡선: 계산된 응력을 적용된 변형률에 대해 플롯하여 응력-변형률 곡선을 만든다. 이 곡선의 초기 선형 부분의 기울기는 영률을 제공한다.

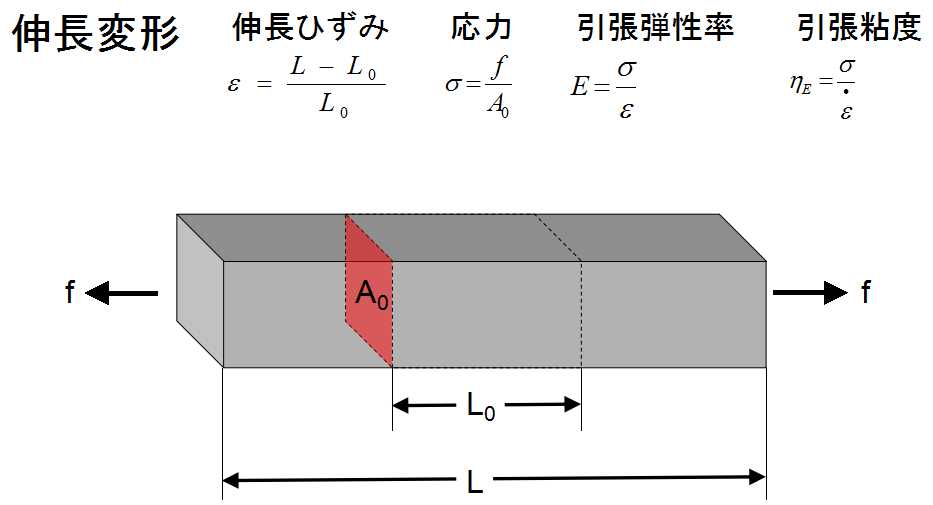
단순한 신장 변형 모델. L_0는 원래 길이, L은 변형 후 길이, ε는 신장 변형률, f는 힘, A_0는 변형 전 힘과 수직인 단면적, σ는 응력, E는 신장 탄성률, η_E는 신장 점도, 위에 점이 찍힌 ε는 신장 변형률의 시간 미분이다.

탄성률은 탄성 변형에서의 응력과 변형률 사이의 비례 상수(응력/변형률)이며, 가해진 외력(응력)을 분자, 응력에 의해 유발된 변형률을 분모로 한 상이다.^[14]

: 탄성률 = 응력/변형률

인장 탄성률

E

는 인장력이나 압축력 등의 단축 응력에 대한 탄성률(영률)이다.

:

E = \frac{\sigma}{\varepsilon}

: 신장 변형률

\varepsilon = \frac{L - L_0}{L_0}

（

L_0

는 원래 길이,

L

는 인장 후 길이）

5. 2. 전단 탄성 계수

전단 탄성 계수(G)는 층밀리기 응력(

\tau

)을 층밀리기 변형도(

\gamma

)로 나누어 구한다.^[20]

:

G \equiv \frac{\tau}{\gamma} = \frac{F/A_0}{\Delta x/h} =  \frac{F h}{\Delta x A_0}

밀도 범함수 이론(DFT)을 통해 재료의 기계적 응력에 대한 반응을 분석하여 전단 탄성 계수를 포함한 다양한 탄성 계수를 계산할 수 있다. VASP, 퀀텀 ESPRESSO, ABINIT와 같은 DFT 소프트웨어를 활용한다.

전단 탄성 계수 (''G'')를 구하는 과정은 다음과 같다.

1. 초기 구조: 재료의 이완된 구조에서 시작한다. 모든 원자는 변형을 가하기 전에 잔류 힘이 없는 최소 에너지 상태여야 한다.

2. 전단 변형 적용: 재료에 작은 간격의 전단 변형을 적용한다. 전단 변형률은 일반적으로 변형률 텐서의 대각선이 아닌 성분이며, 결정 셀의 부피가 아닌 모양에 영향을 미친다.^[6]

3. 응력 계산: 적용된 전단 변형률이 있는 각 구성에 대해, DFT 계산을 수행하여 결과 응력 텐서를 결정한다.

4. 전단 응력 vs. 전단 변형률 곡선: 각 증가에 대해 계산된 전단 응력을 적용된 전단 변형률에 대해 플롯한다. 선형 영역에서 응력-변형률 곡선의 기울기는 전단 탄성 계수를 제공하며, ''G''=''τ''/''γ''이고, 여기서 ''τ''는 전단 응력이고 ''γ''는 적용된 전단 변형률이다.

전단 탄성 계수는 전단력에 대한 탄성률을 의미하며, 강성률(전단 탄성 계수, 가로 탄성 계수, 전단 탄성 계수, 라메의 제 2 상수)로도 불린다.

:

G = \frac{\sigma}{\gamma}

전단 변형률: $\gamma = \frac{d}{h} = \tan \alpha$ (d는 전단으로 인해 면이 전단력 방향으로 이동한 거리, h는 전단력 방향과 수직인 시료 두께, α는 시료의 면이 직사각형에서 평행사변형이 될 때의 기울어진 각도)
전단 점도: $\eta = \frac{\sigma}{d\gamma/dt}$

5. 3. 체적 탄성 계수

물체의 부피 변화에 저항하려는 강성(stiffness)을 특별히 그 물체의 체적 탄성 계수(K)라고 부른다. 체적 탄성 계수는 체적 응력을 체적 변형률로 나눈 값으로 정의되며, 압축성의 역수이다. 체적 탄성 계수는 영률을 3차원으로 확장한 것이다.^[7]

체적 탄성 계수(

K

)는 다음과 같이 정의된다.

:

K = \frac{\sigma}{\kappa}

여기서,

$\sigma$ 는 응력
$\kappa$ 는 체적 변형률
체적 변형률 $\kappa = \frac{V - V_0}{V_0}$ ( $V_0$ 는 원래 부피, $V$ 는 변형 후 부피)
체적 점도 $\eta_V = \frac{\sigma}{d\kappa/dt}$

밀도 범함수 이론(DFT)은 재료의 체적 탄성 계수를 결정하는 신뢰할 수 있는 방법을 제공한다. VASP, 퀀텀 ESPRESSO, 또는 ABINIT와 같은 DFT 소프트웨어를 활용하여 계산할 수 있다.

체적 탄성 계수 계산 방법은 다음과 같다.

1. 초기 구조: 재료의 이완된 구조에서 시작한다. 재료가 완전히 최적화되어야 한다.

2. 부피 변화: 결정 구조의 부피를 점진적으로 변경하여 압축하거나 확장한다.

3. 압력 계산: 변경된 각 부피에 대해, 해당 부피를 유지하는 데 필요한 압력을 결정하기 위해 DFT 계산을 수행한다.

4. 압력-부피 곡선: 적용된 압력을 결과 부피 변화에 대해 플롯한다. 체적 탄성 계수는 선형 탄성 영역에서 이 곡선의 기울기로부터 계산할 수 있다.

5. 4. 굽힘 탄성 계수

모멘트가 작용할 때 물체가 구부러지는 경향을 설명하는 것은 굽힘 탄성 계수( ''E''_flex)이다.^[1]

5. 5. 라메 상수

라메의 첫 번째 매개변수 λ는 기타 탄성 계수 중 하나이다.^[14]

6. 탄성 계수의 관계식

등방성 재료에서 인장 탄성 계수(E)와 층밀리기 탄성 계수(G) 사이에는 다음과 같은 관계가 성립한다.^[20]^[21]

:G^영어 = E^영어 / (2 * (1 + v^영어))

여기서 v^영어는 재료의 푸아송 비이다.

일반적으로 등방성 물질(무정형 폴리머, 비정질·무배향 폴리머 등)의 경우 3가지 탄성률(인장 탄성률 E^영어, 전단 탄성률 G^영어, 체적 탄성률 K^영어) 간의 관계는 다음과 같다.^[14]

:E^영어 = 2G^영어(1 - v^영어) = 3K^영어(1 - 2v^영어)

여기서 v^영어는 종방향 변형률과 횡방향 변형률의 비(푸아송 비)이다. 결정성 폴리머, 섬유, 필름, 섬유 충전 복합 재료, 일반 사출 성형품 등은 등방성 물질이 아니다. 고분자 사슬, 충전 섬유, 결정상 등에 배향성을 가지며, 그 정도는 내부와 표면에서 다르게 나타난다. 이러한 이방성 물질은 2개 이상의 독립된 탄성률을 갖는다.^[15]

재료가 등방 균질 탄성 재료라고 가정하면, 탄성률 텐서 '''''D'''''의 독립 성분은 2개로 제한되고^[12], 다음 식으로 쓸 수 있다.^[13]

:D^영어 = λδ^영어δ^영어 + G^영어(δ^영어δ^영어 + δ^영어δ^영어)

여기서 δ는 크로네커 델타이다.

이 경우, 영률 ''E'', 푸아송 비 ν, 체적 탄성률 ''K'', 강성률 ''G'', 라메의 제1상수 λ의 5개의 탄성률은 각각 2개를 사용하여 나머지 3개를 나타낼 수 있다.

등방 균질 탄성체의 각 탄성률 간의 변환식
	$E$ （영률）	$\nu$ （푸아송 비）	$K$ （체적 탄성률）	$G$ （강성률）	$\lambda$ （라메의 제1상수）
$E, \nu$	$E$	$\nu$	$\dfrac{E}{3(1-2\nu)}$	$\dfrac{E}{2(1+\nu)}$	$\dfrac{E\nu}{(1+\nu)(1-2\nu)}$
$E, K$	$E$	$\dfrac{3K-E}{6K}$	$K$	$\dfrac{3K E}{9K-E}$	$\dfrac{3K(3K-E)}{9K-E}$
$E, G$	$E$	$\dfrac{E-2G}{2G}$	$\dfrac{G E}{3(3G-E)}$	$G$	$\dfrac{G(E-2G)}{3G-E}$
$E, \lambda$	$E$	$\dfrac{2\lambda}{E+\lambda+\alpha}$	$\dfrac{E+3\lambda+\alpha}{6}$	$\dfrac{E-3\lambda+\alpha}{4}$	$\lambda$
$\nu, K$	$3K(1-2\nu)$	$\nu$	$K$	$\dfrac{3K(1-2\nu)}{2(1+\nu)}$	$\dfrac{3K\nu}{1+\nu}$
$\nu, G$	$2G(1+\nu)$	$\nu$	$\dfrac{2G(1+\nu)}{3(1-2\nu)}$	$G$	$\dfrac{2G\nu}{1-2\nu}$
$\nu, \lambda$	$\dfrac{\lambda(1+\nu)(1-2\nu)}{\nu}$	$\nu$	$\dfrac{\lambda(1+\nu)}{3\nu}$	$\dfrac{\lambda(1-2\nu)}{2\nu}$	$\lambda$
$K, G$	$\dfrac{9KG}{3K+G}$	$\dfrac{3K-2G}{6K+2G}$	$K$	$G$	$K-\frac{2}{3}G$
$K, \lambda$	$\dfrac{9(K-\lambda)}{3K-\lambda}$	$\dfrac{\lambda}{3K-\lambda}$	$K$	$\frac{3}{2}(K-\lambda)$	$\lambda$
$G, \lambda$	$\dfrac{G(3\lambda+2G)}{\lambda+G}$	$\dfrac{\lambda}{2\lambda+2G}$	$\dfrac{3\lambda+2G}{3}$	$G$	$\lambda$

7. 탄성 계수 계산

탄성 계수(E)는 인장 응력( $\sigma$ )을 인장 변형도( $\varepsilon$ )로 나누어 구할 수 있다.^[18]^[19]

: $E = \frac{\sigma}{\varepsilon}= \frac{F/A_0}{\Delta l/l_0} = \frac{F l_0} {A_0 \Delta l}$

탄성 계수 E의 단위는 파스칼이며, F는 작용하는 하중, A₀은 단면적, $\Delta l$ 는 재료의 길이 변화량, l₀은 재료의 원래 길이이다.

전단 탄성 계수, 또는 층밀리기 탄성 계수(G)는 층밀리기 응력( $\tau$ )을 층밀리기 변형도( $\gamma$ )로 나누어 구한다.^[20]

: $G \equiv \frac{\tau}{\gamma} = \frac{F/A_0}{\Delta x/h} = \frac{F h}{\Delta x A_0}$

물체의 부피변화에 저항하려는 강성(stiffness)을 특별히 그 물체의 부피 탄성 계수(K)라고 부른다.

밀도 범함수 이론(DFT)은 재료의 기계적 응력에 대한 반응의 특징을 나타내는 여러 형태의 탄성 계수를 결정하는 신뢰할 수 있는 방법을 제공한다. VASP, 퀀텀 ESPRESSO, 또는 ABINIT와 같은 DFT 소프트웨어를 활용한다.

영률(E) - 특정 축을 따라 격자 매개변수에 작고 점진적인 변화를 적용하고 DFT를 사용하여 해당하는 응력 반응을 계산한다. 영률은 ''E''=''σ''/''ϵ''로 계산되며, 여기서 ''σ''는 응력이고 ''ϵ''는 변형률이다.^[4]
전단 탄성 계수(G) - 재료에 작은 간격의 전단 변형을 적용한다. 선형 영역에서 응력-변형률 곡선의 기울기는 전단 탄성 계수를 제공하며, ''G''=''τ''/''γ''이고, 여기서 ''τ''는 전단 응력이고 ''γ''는 적용된 전단 변형률이다.
체적 탄성 계수(K) - 결정 구조의 부피를 점진적으로 변경하여 압축하거나 확장한다. 체적 탄성 계수는 ''K''=−''VdV''/''dP''로 정의되며, 여기서 ''V''는 원래 부피이고, ''dP''는 압력의 변화이며, ''dV''는 부피의 변화이다.^[7]

8. 복소 탄성 계수

점탄성에서는 탄성률을 복소수로 나타낸다. 복소 탄성률의 실수부는 저장 탄성률, 허수부는 손실 탄성률이라고 부른다.

참조

_[1] 서적 The science and engineering of materials https://books.google[...] Cengage Learning
_[2] 서적 Mechanics of Materials https://archive.org/[...] McGraw Hill
_[3] 서적 Elastic constants and their measurement McGraw-Hill 1974
_[4] 간행물 A Review on the Modeling of the Elastic Modulus and Yield Stress of Polymers and Polymer Nanocomposites: Effect of Temperature, Loading Rate and Porosity 2022-01-18
_[5] 간행물 DFT insights into the electronic structure, mechanical behaviour, lattice dynamics and defect processes in the first Sc-based MAX phase Sc2SnC 2022-08-18
_[6] 간행물 DFT based comparative analysis of the physical properties of some binary transition metal carbides XC (X = Nb, Ta, Ti) 2023-05
_[7] 간행물 Elastic properties of bulk and low-dimensional materials using van der Waals density functional 2018-07-12
_[8] 서적 機械工学辞典丸善
_[9] 문서 固体の弾塑性力学数理工学社
_[10] 문서 총화규약
_[11] 문서 異方性材料の弾性論 코로나社
_[12] 웹사이트 構成方程式の基本知識―考え方と定式化― http://c-pc8.civil.t[...] 2020-04-26
_[13] 문서 自然災害のシミュレーション入門朝倉書店
_[14] 간행물 入門講座　弾性率および粘弾性 https://doi.org/10.1[...] 1988-11
_[15] 서적 高分子と複合材料の力学的性質化学同人 1980
_[16] 웹사이트 한국물리학회 물리학용어집 https://www.kps.or.k[...]
_[17] 웹사이트 한국물리학회 물리학용어집 https://www.kps.or.k[...]
_[18] 서적 SI 재료역학 센게이지 러닝 코리아 2017-09-09
_[19] 서적 SI 재료역학 센게이지 러닝 코리아 2017-09-09
_[20] 서적 SI 재료역학 센게이지 러닝 코리아 2017-09-09
_[21] 서적 강구조설계 구미서관 2017-09-09

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com