탐색적 자료 분석
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
탐색적 자료 분석(EDA)은 자료를 사용하여 검증할 가설을 제시하는 데 중점을 둔 통계적 접근 방식이다. 존 튜키가 1977년 저술한 책을 통해 널리 알려졌으며, 통계적 가설 검정에 치중하는 기존 방식에 대한 대안으로 제시되었다. EDA는 자료에서 예상치 못한 발견을 가능하게 하고, 현상의 원인에 대한 가설을 제안하며, 통계적 추론의 기초가 되는 가정을 평가하는 등의 목적을 가진다. 상자 그림, 히스토그램, 산점도 등 다양한 시각적, 정량적 기법을 활용하며, 데이터 마이닝과 통계적 사고 교육에도 활용된다.
더 읽어볼만한 페이지
| 탐색적 자료 분석 | |
|---|---|
| 개요 | |
| 유형 | 통계학 |
| 분야 | 자료 분석 |
| 목적 | |
| 주요 목표 | 자료의 주요 특징 요약 자료에 대한 더 깊은 이해 도모 적절한 통계 모델 개발 가설 정의 추가 자료 수집 필요성 판단 |
| 기법 | |
| 주요 기법 | 다양한 그래프 사용 자료 요약 및 시각화 간단한 통계 모형 적용 |
| 중요성 | |
| 중요성 | 분석적 방법론의 적절한 사용 보장 자료의 숨겨진 구조 발견 변수 중요도 추출 이상치 및 비정상적인 관측치 식별 기본 가정 검증 |
| 관련 분야 | |
| 관련 분야 | 자료 시각화 기술 통계학 통계적 추론 자료 마이닝 |
2. 역사
존 튜키는 1977년에 《탐색적 자료 분석》이라는 책을 저술하여 탐색적 자료 분석(EDA)의 개념을 널리 알렸다.[6] 튜키는 통계학이 통계적 가설 검정 (확증적 자료 분석)에만 치우치는 것을 비판하고, 자료를 통해 검정할 가설을 발견하는 EDA의 중요성을 강조했다. 그는 두 가지 분석 유형을 혼동하여 동일한 데이터 집합에 적용하면 체계적 오류가 발생할 수 있다고 경고했다.[6]
튜키 이전에도 여러 학자들이 EDA의 초기 아이디어에 기여했다.
| 인물 | 기여 |
|---|---|
| 프랜시스 골턴 | 순서 통계량과 분위수 강조 |
| 아서 라이언 보울리 | 줄기 잎 그림과 다섯 숫자 요약의 전신 사용 (7수치 요약 사용) |
| 앤드류 에렌버그 | 자료 축약의 철학 명확화 |
오픈 대학교의 "사회 속의 통계학" 강좌는 고트프리트 뇌터의 연구를 통합하여 동전 던지기와 중앙값 검정을 통해 통계적 추론을 소개했다.
튜키는 1961년에 데이터 분석을 "데이터 분석 절차, 그러한 절차의 결과를 해석하는 기술, 데이터 분석을 더 쉽고, 더 정확하고, 더 정밀하게 만들기 위한 데이터 수집 계획 방법, 그리고 데이터 분석에 적용되는 (수학적) 통계의 모든 메커니즘과 결과"로 정의했다.[3]
튜키가 EDA를 옹호하면서, 벨 연구소의 S와 같은 통계적 컴퓨팅 패키지 개발이 촉진되었다.[4] S 프로그래밍 언어는 S-PLUS와 R 시스템에 영감을 주었다. 이러한 통계 컴퓨팅 환경은 동적 시각화 기능이 크게 개선되어 통계학자들이 데이터의 이상치, 추세 및 패턴을 식별하여 추가 연구를 수행할 수 있도록 지원했다.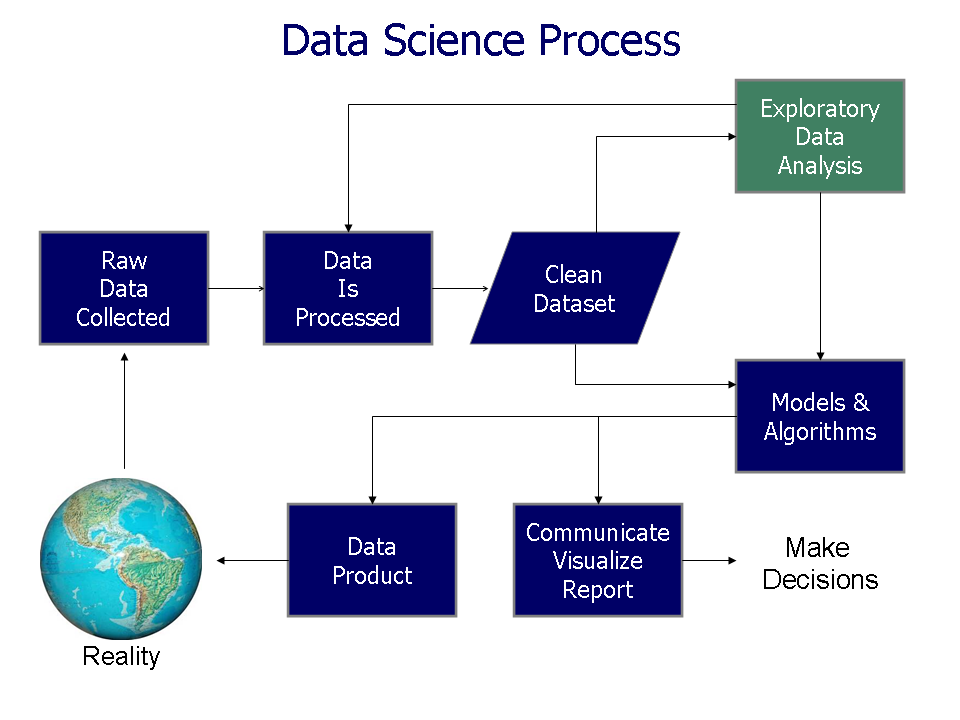
EDA의 목표는 다음과 같다.[7]
- 데이터에서 예상치 못한 발견
- 관찰된 현상의 인과 관계에 대한 가설 제시
- 통계적 추론의 기반이 될 가정 평가
- 적절한 통계 도구 및 기법 선택 지원
- 설문 조사 또는 실험 설계를 통한 추가적인 자료 수집 기반 제공
많은 EDA 기법이 데이터 마이닝에 채택되었으며, 어린 학생들에게 통계적 사고를 소개하는 방법으로도 활용되고 있다.[8]
2. 1. 통계적 배경
터키의 EDA는 강건 통계와 비모수 통계라는 두 가지 통계적 이론의 발전과 관련이 있었다. 이 두 이론은 모두 통계 모델 공식화 과정에서의 오류에 대한 통계적 추론의 민감도를 줄이고자 했다.[5] 터키는 수치 데이터의 다섯 숫자 요약 (최솟값, 최댓값, 중앙값, 사분위수) 사용을 장려했다. 중앙값과 사분위수는 경험적 분포 함수의 함수이므로, 평균 및 표준 편차와 달리 모든 분포에 대해 정의되기 때문이다. 또한 사분위수와 중앙값은 전통적인 요약(평균과 표준 편차)보다 왜도 또는 꼬리가 두꺼운 분포에 더 강건하다.[5]S, S-PLUS, R 패키지에는 퀴누이와 터키의 잭나이프 및 에프론의 부트스트래핑과 같은 재표본 추출 통계를 사용하는 루틴이 포함되어 있다. 이러한 통계 기법은 비모수적이고 강건하다(많은 문제에 대해).[5]
탐색적 데이터 분석, 강건 통계, 비모수 통계 및 통계 프로그래밍 언어의 개발은 통계학자들이 과학 및 공학 문제를 해결하는 데 도움이 되었다. 이러한 문제에는 벨 연구소와 관련된 반도체 제조 및 통신 네트워크 이해가 포함되었다. 이러한 통계적 발전은 모두 터키가 옹호했으며, 라플라스 전통의 지수족에 대한 강조와 같은 통계적 가설 검정 이론을 보완하도록 설계되었다.[5]
3. 목적과 특징
존 튜키는 1977년에 출간한 《탐색적 자료 분석》에서 통계학이 확인적 자료 분석(통계적 가설 검정)에만 치중되어 있다고 지적하며, 자료를 통해 가설을 제시하는 데 더 많은 গুরুত্ব를 두어야 한다고 주장했다.[6] 특히, 그는 두 가지 분석 유형을 혼동하여 동일한 데이터 집합에 적용하면 체계적 오류를 일으킬 수 있다고 경고했다.[17]
EDA의 주요 목적은 다음과 같다.
- 데이터에서 예상치 못한 발견을 가능하게 한다.
- 관찰된 현상의 인과 관계에 대한 가설을 제시한다.
- 통계적 추론의 기반이 될 가정을 평가한다.
- 적절한 통계 도구 및 기법 선택을 지원한다.
- 설문 조사나 실험 설계를 통해 추가적인 자료 수집의 기반을 제공한다.[7]
EDA는 특정 기법보다는 접근 방식에 중점을 둔다.[18] 즉, 정해진 절차를 따르기보다는 데이터를 자유롭게 탐색하며 특징을 파악하는 것이 중요하다. 많은 EDA 기법이 데이터 마이닝에 채택되었으며, 어린 학생들에게 통계적 사고를 소개하는 방법으로도 활용되고 있다.[8]
Cook 등의 연구진은 식사 모임에서 웨이터에게 주는 팁을 예측하는 변수를 찾는 연구를 진행했다.[12] 이들은 팁 금액, 총 청구액, 지불자 성별, 흡연/비흡연 구역, 시간대, 요일, 모임 규모 등의 변수를 수집했다. 회귀 모델 분석 결과, 모임 규모가 커질수록 팁 비율이 감소하는 경향을 발견했다.
그러나 데이터를 탐색하면서 모델로는 설명되지 않는 흥미로운 특징들이 발견되었다. 예를 들어, 팁 금액의 히스토그램에서는 정수 달러와 반 달러 금액에서 피크가 나타났는데, 이는 고객들이 팁을 반올림된 숫자로 선택하는 경향 때문이었다. 또한, 팁과 청구액의 산점도에서는 팁 금액이 증가함에 따라 변동성이 커지는 이분산성이 관찰되었으며, 흡연 여부와 지불자의 성별에 따라서도 팁의 변동성에 차이가 있었다.
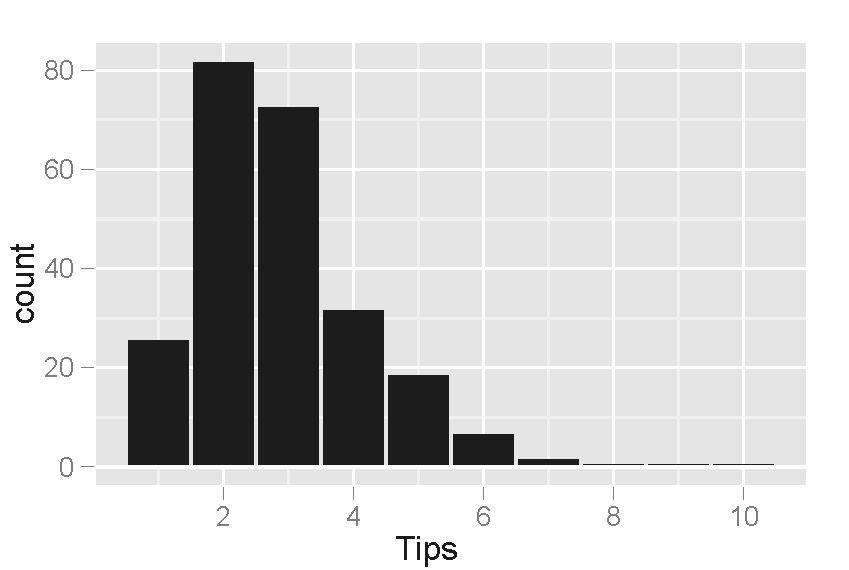
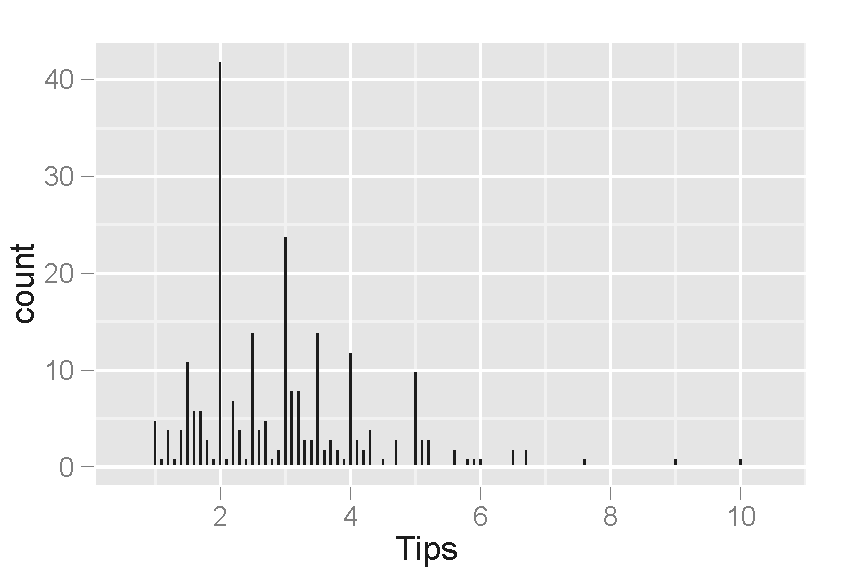
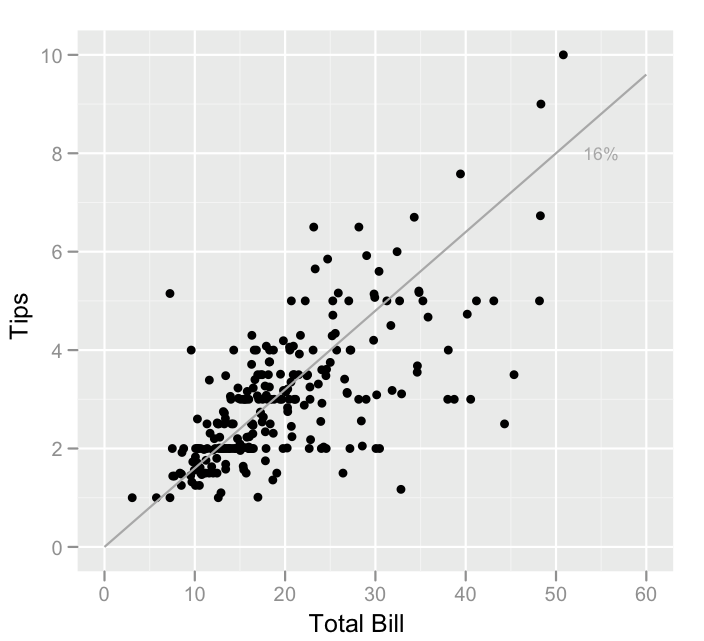
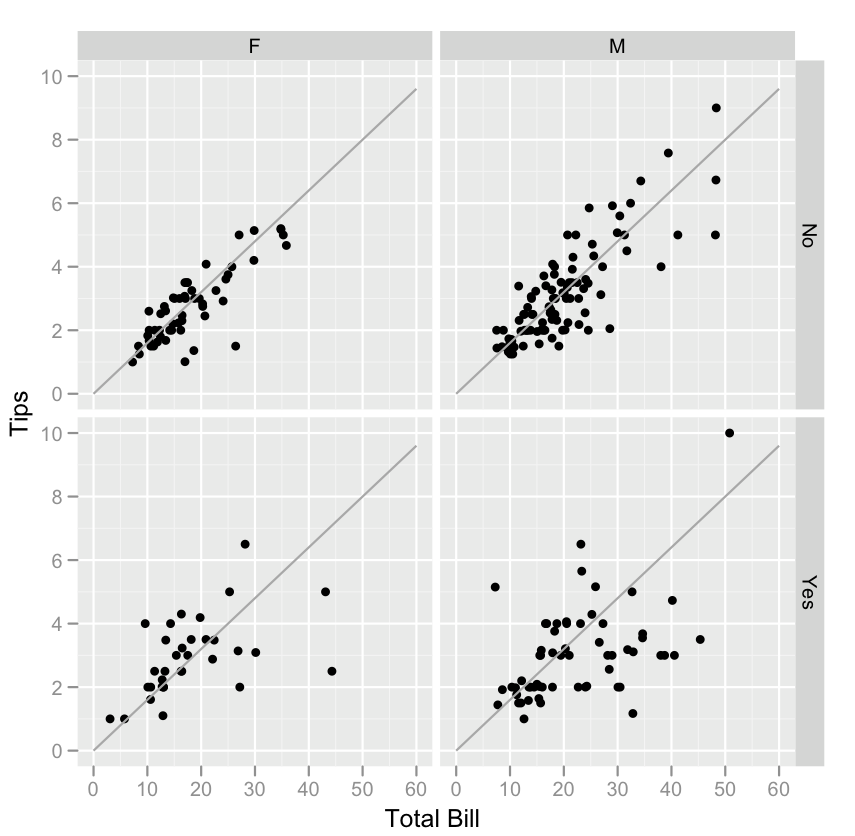
이러한 패턴들은 사전에 예상하기 어려웠던 팁에 대한 새로운 가설을 제시하며, 추가적인 데이터 수집 및 분석을 통해 검증할 수 있다.
4. 기법 및 도구
탐색적 자료 분석(EDA)은 특정 기법보다는 데이터에 대한 접근 방식에 의해 그 특징이 더 잘 드러난다.[9] EDA는 데이터를 깊이 이해하고 숨겨진 패턴을 발견하는 데 중요한 역할을 한다.
EDA에는 다음과 같은 기법들이 활용된다.
- 시각적 기법
- 차원 축소
- 정량적 기법
쿡 등의 연구진은 웨이터에게 주는 팁을 예측하는 변수를 찾는 연구에서 EDA를 활용했다.[12] 이들은 팁 금액, 총 청구액, 지불자 성별, 흡연/비흡연 구역, 시간대, 요일, 모임 규모 등의 데이터를 수집했고, 회귀 모델을 통해 모임 규모가 커질수록 팁 비율이 감소하는 경향을 확인했다.
그러나 EDA를 통해 이 모델로는 설명되지 않는 다른 특징들이 발견되었다. 팁 금액 히스토그램에서는 고객들이 팁을 반올림된 숫자로 선택하는 경향 때문에 정수 및 반 달러 금액에서 피크가 나타났다. 팁 대 청구액 산점도에서는 팁 금액 변동성이 증가하는 이분산성이 확인되었고, 지불자 성별과 흡연 구역에 따른 팁 제공 경향 차이도 발견되었다. 이러한 패턴들은 추가적인 실험 및 데이터 수집을 통해 검증할 가설을 제시한다.
4. 1. 시각적 기법
탐색적 자료 분석(EDA)에서는 데이터의 패턴과 특징을 파악하기 위해 다양한 시각적 도구를 활용한다.EDA에 사용되는 일반적인 그래픽 기법은 다음과 같다.[9]
| 기법 | 설명 |
|---|---|
| 상자 그림 | 데이터의 분포와 이상치를 시각적으로 보여준다. |
| 히스토그램 | 데이터 값의 빈도를 막대 그래프 형태로 나타낸다. |
| 다변량 차트 | 여러 변수 간의 관계를 한 번에 보여준다. |
| 런 차트 | 시간 경과에 따른 데이터 변화를 보여준다. |
| 파레토 차트 | 문제의 원인 빈도를 내림차순으로 정렬하여 보여준다. |
| 산점도 (2D/3D) | 두 변수(2D) 또는 세 변수(3D) 간의 관계를 점으로 나타낸다. |
| 줄기 잎 그림 | 데이터를 줄기와 잎 형태로 나타내어 분포를 보여준다. |
| 평행 좌표 | 다변량 데이터를 평행 축에 나타내어 변수 간 관계를 시각화한다. |
| 오즈비 | 두 그룹 간의 특정 사건 발생 확률 비율을 비교한다. |
| 타겟 투영 추구 | 고차원 데이터를 저차원 공간에 투영하여 패턴을 찾는다. |
| 히트맵 | 데이터 값을 색상으로 표현하여 패턴을 시각화한다. |
| 막대 그래프 | 범주형 데이터를 막대 형태로 나타낸다. |
| 수평선 그래프 | 시계열 데이터의 변화를 한눈에 보여준다. |
| 글리프 기반 시각화 (PhenoPlot[10], 체르노프 얼굴 등) | 여러 변수를 사람 얼굴 표정 등 글리프 형태로 나타내어 패턴을 찾는다. |
| 투영 방법 (그랜드 투어, 가이드 투어, 수동 투어 등) | 고차원 데이터를 다양한 각도에서 투영하여 패턴을 찾는다. |
이러한 그래프들은 데이터의 분포, 변수 간 관계, 이상치, 군집 등 다양한 특징을 파악하는 데 도움을 준다. 예를 들어, 팁 금액과 청구액 간의 관계를 나타낸 산점도를 통해 팁 금액의 변동성이 청구액에 따라 증가하는 이분산성을 확인할 수 있다.[12] 또한, 흡연 여부와 지불자 성별에 따라 팁을 주는 경향에 차이가 있음을 알 수 있다.
이처럼 EDA의 시각적 기법은 데이터를 다양한 각도에서 살펴보고, 통계 모델로는 설명되지 않는 숨겨진 패턴이나 가설을 발견하는 데 유용하다.
4. 1. 1. 차원 축소
다차원 척도법주성분 분석 (PCA)
Multilinear principal component analysis|멀티리니어 주성분 분석영어
Nonlinear dimensionality reduction|비선형 차원 축소영어 (NLDR)
Iconography of correlations|상관 아이코노그래피영어
4. 2. 정량적 기법
중앙값 폴리시[20], 트리미안[20], 정렬[20]은 데이터를 요약하고 분석하는 정량적 기법이다.5. 응용 분야
EDA는 여러 분야에서 널리 활용되고 있다. 데이터 마이닝 분야에 많은 기법이 채택되었으며,[8] 머신 러닝의 전처리 과정에서도 중요한 역할을 한다. 통계적 사고 교육에도 EDA 기법이 도입되어 어린 학생들에게도 가르치고 있다.[8]
벨 연구소에서는 반도체 제조 및 통신 네트워크 연구와 같은 과학 및 공학 문제 해결에 EDA를 활용했다.[5] 특히, 터키가 EDA를 옹호하면서 S, S-PLUS, R과 같은 통계적 컴퓨팅 패키지 개발에 영향을 주었다.[4] 이러한 통계 컴퓨팅 환경은 동적 시각화 기능을 통해 데이터의 이상치, 추세, 패턴 등을 파악하여 추가 연구를 돕는다.
대한민국에서도 EDA는 빅데이터 분석, 머신러닝 등의 분야에서 데이터 전처리 및 초기 분석 단계에 필수적으로 활용되고 있다.
6. 소프트웨어
존 튜키는 EDA를 옹호하면서, 벨 연구소의 S와 같은 통계적 컴퓨팅 패키지 개발을 장려했다.[4] S 프로그래밍 언어는 S-PLUS와 R 시스템에 영감을 주었다. 이러한 통계 컴퓨팅 환경은 통계학자들이 데이터의 이상치, 추세 및 패턴을 식별할 수 있도록 동적 시각화 기능을 크게 개선했다.[4]
EDA를 위한 다양한 소프트웨어 도구가 개발되어 있다. 다음은 그 목록이다.
| 소프트웨어 | 설명 |
|---|---|
| JMP | SAS 인스티튜트의 EDA 패키지 |
| KNIME | 콘스탄츠 정보 마이너 – 이클립스 기반의 오픈 소스 데이터 탐색 플랫폼 |
| 미니탭 | 산업 및 기업 환경에서 널리 사용되는 EDA 및 일반 통계 패키지 |
| 오렌지 | 오픈 소스 소프트웨어 데이터 마이닝 및 머신 러닝 소프트웨어 제품군 |
| 파이썬 | 데이터 마이닝 및 머신 러닝에 널리 사용되는 오픈 소스 프로그래밍 언어 |
| R | 통계 컴퓨팅 및 그래픽을 위한 오픈 소스 프로그래밍 언어. 파이썬과 함께 데이터 과학 분야에서 가장 인기 있는 언어 중 하나 |
| 팅커플롯 | 초등학교 고학년 및 중학생을 위한 EDA 소프트웨어 |
| Weka | 타겟 프로젝션 퍼슈트와 같은 시각화 및 EDA 도구를 포함하는 오픈 소스 데이터 마이닝 패키지 |
| Visplore | 대규모 시계열 데이터를 위한 EDA 소프트웨어 |
7. 관련 개념
존 튜키는 1961년에 데이터 분석을 "데이터 분석 절차, 그러한 절차의 결과를 해석하는 기술, 데이터 분석을 더 쉽고, 더 정확하게 만들 데이터를 수집하는 계획 방법, 그리고 데이터 분석에 적용되는 (수학적) 통계의 모든 메커니즘과 결과"로 정의했다.[3]
튜키의 EDA 옹호는 벨 연구소의 S 언어와 같은 통계 계산 패키지 개발을 뒷받침했다.[4] S 프로그래밍 언어는 S-PLUS와 R 시스템에 영향을 미쳤다. 이 통계 계산 환경은 개선된 동적 시각화 기능을 갖추고 있어, 통계학자들이 추가 연구가 필요한 데이터의 이상치, 추세, 패턴을 식별할 수 있게 했다.
튜키의 EDA는 강건 통계와 비모수 통계학과 관련이 있다. 이들은 모두 통계 모델 공식화 과정에서 발생하는 오류에 대한 통계적 추론의 민감도를 줄이고자 했다. 튜키는 수치 데이터의 다섯 숫자 요약(극값 (최댓값과 최솟값), 중앙값, 사분위수) 사용을 장려했다. 중앙값과 사분위수는 경험적 분포 함수이므로, 평균과 표준 편차와 달리 모든 분포에 대해 정의된다. 또한 사분위수와 중앙값은 평균과 표준 편차보다 왜곡된 분포나 꼬리가 두꺼운 분포에 더 강건하다. S, S-PLUS, R 패키지에는 에프론의 부트스트랩법 등 비모수적이고 강건한 재표본 추출 통계를 사용하는 루틴이 포함되어 있다.
탐색적 데이터 분석, 강건 통계, 비모수 통계, 통계 프로그래밍 언어 개발은 통계학자들이 과학 및 공학 문제에 더 쉽게 접근하도록 도왔다. 여기에는 벨 연구소와 관련된 반도체 제조 및 통신 네트워크 이해가 포함된다. 이러한 통계적 발전은 모두 튜키가 주장한 것으로, 통계적 가설 검정에 관한 해석 이론, 특히 지수족에 대한 라플라스의 강조를 보완하기 위해 설계되었다.[16]
탐색적 자료 분석과 관련된 개념은 다음과 같다.
- 앤스콤의 예 - 탐색의 중요성을 보여주는 예시이다.
- 데이터 드레징 - 통계적으로 유의미한 결과만 보고하는 데이터 분석의 오용 사례이다.
- 예측 분석 - 현재와 과거의 사실을 바탕으로 미래를 예측하는 분석 기법이다.
- 구조적 데이터 분석 (통계학) - 주어진 데이터에 적합한 구조를 탐색하여 비교, 예측, 조작 등에 사용하는 분석 기법이다.
- 구성 빈도 분석 - 우연으로 예상되는 것보다 현저히 많거나 적은 패턴을 감지하여 구조에 대한 통찰력을 얻는 분석 기법이다.
- 기술 통계 - 표본 분포의 특징을 정량적으로 묘사하고 요약하는 통계값으로, EDA의 기초가 된다.
참조
[1]
서적
Problem Solving: A Statistician's Guide
Chapman and Hall
[2]
논문
Ten simple rules for initial data analysis
[3]
문서
John Tukey-The Future of Data Analysis-July 1961
http://projecteuclid[...]
[4]
간행물
A Brief History of S
http://www2.research[...]
AT&T Bell Laboratories
2015-07-23
[5]
논문
Conversation with John W. Tukey and Elizabeth Tukey, Luisa T. Fernholz and Stephan Morgenthaler
[6]
서적
Exploratory Data Analysis
Pearson
[7]
문서
Behrens-Principles and Procedures of Exploratory Data Analysis-American Psychological Association-1997
https://web.archive.[...]
[8]
논문
Statistics goes to school
[9]
논문
We need both exploratory and confirmatory
[10]
논문
Visualizing cellular imaging data using PhenoPlot
2015-01-08
[11]
문서
Elementary Manual of Statistics
https://archive.org/[...]
[12]
문서
Cook, D. and Swayne, D.F. (with A. Buja, D. Temple Lang, H. Hofmann, H. Wickham, M. Lawrence) (2007) ″Interactive and Dynamic Graphics for Data Analysis: With R and GGobi″ Springer, 978-0387717616
[13]
서적
Problem Solving: A Statistician's Guide
Chapman and Hall
[14]
논문
Ten simple rules for initial data analysis
[15]
문서
John Tukey-The Future of Data Analysis-July 1961
http://projecteuclid[...]
[16]
논문
Conversation with John W. Tukey and Elizabeth Tukey, Luisa T. Fernholz and Stephan Morgenthaler
[17]
서적
Exploratory Data Analysis
Pearson
[18]
문서
Behrens-Principles and Procedures of Exploratory Data Analysis-American Psychological Association-1997
https://web.archive.[...]
[19]
논문
Statistics goes to school
[20]
논문
We need both exploratory and confirmatory
[21]
논문
Visualizing cellular imaging data using PhenoPlot
2015-01-08
[22]
문서
Elementary Manual of Statistics
https://archive.org/[...]
[23]
문서
Cook, D. and Swayne, D.F. (with A. Buja, D. Temple Lang, H. Hofmann, H. Wickham, M. Lawrence) (2007) ″Interactive and Dynamic Graphics for Data Analysis: With R and GGobi″ Springer, 978-0387717616
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com