토질역학

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

토질역학은 흙의 물리적, 역학적 성질을 연구하고 이를 공학적 문제에 적용하는 학문이다. 흙의 생성과 구성, 흙의 분류, 흙의 삼상 관계, 흙의 투수성, 유효응력과 모관 현상, 흙의 압밀, 흙의 전단 거동 등을 다룬다. 토질역학은 옹벽, 기초, 사면 안정 등 다양한 공학 분야에 적용되며, 최근에는 동역학계 기반 토질역학(DSSM) 연구가 진행되고 있다.

더 읽어볼만한 페이지

토질역학 - 산사태
산사태는 사면 안정성 훼손으로 발생하는 자연재해로, 자연적, 인위적 요인에 의해 발생하며, 다양한 유형으로 분류되고 인명 및 재산 피해를 야기하므로, 사전 예방과 위험 지역 관리가 중요하다.
토질역학 - 점토
점토는 2~5µm 이하의 미세한 토양 입자로, 층상 규산염 광물을 주성분으로 하며, 다양한 분야에서 정의와 분류 기준이 다르고, 가소성과 소성능력, 흡착성, 이온 교환 능력을 활용하여 건축, 화장품, 의약품 등 다양한 용도로 사용되지만, 특정 점토는 토목 공사에 문제를 일으키기도 한다.

토질역학
개요
분야	토질역학 및 응용 역학의 한 분야
설명	흙의 거동을 다루는 학문
관련 학문	지반공학, 지질학
주요 내용
구성 요소	흙 입자, 물, 공기
기본 개념	유효 응력, 투수 계수, 다짐, 전단 강도
응용 분야	기초공학, 사면 안정, 터널 공학, 지반 개량
추가 정보
관련 서적	Soils and Waves: Particulate Materials Behavior, Characterization and Process Monitoring Introductory Geotechnical Engineering
참고 자료	Theory of Effective Stress in Soil and Rock and Implications for Fracturing Processes: A Review

2. 흙의 생성과 구성

흙은 암석의 풍화 작용으로 생성된 입자와 물, 공기로 구성된다. 흙 입자는 다양한 광물로 이루어져 있으며, 물과 공기는 흙 입자 사이의 공간인 공극(간극)을 채운다.^[1] 흙은 생성된 위치에 그대로 남아있는 잔류토와 중력, 물, 바람, 빙하 등에 의해 운반된 충적토, 뢰스 등으로 구분된다.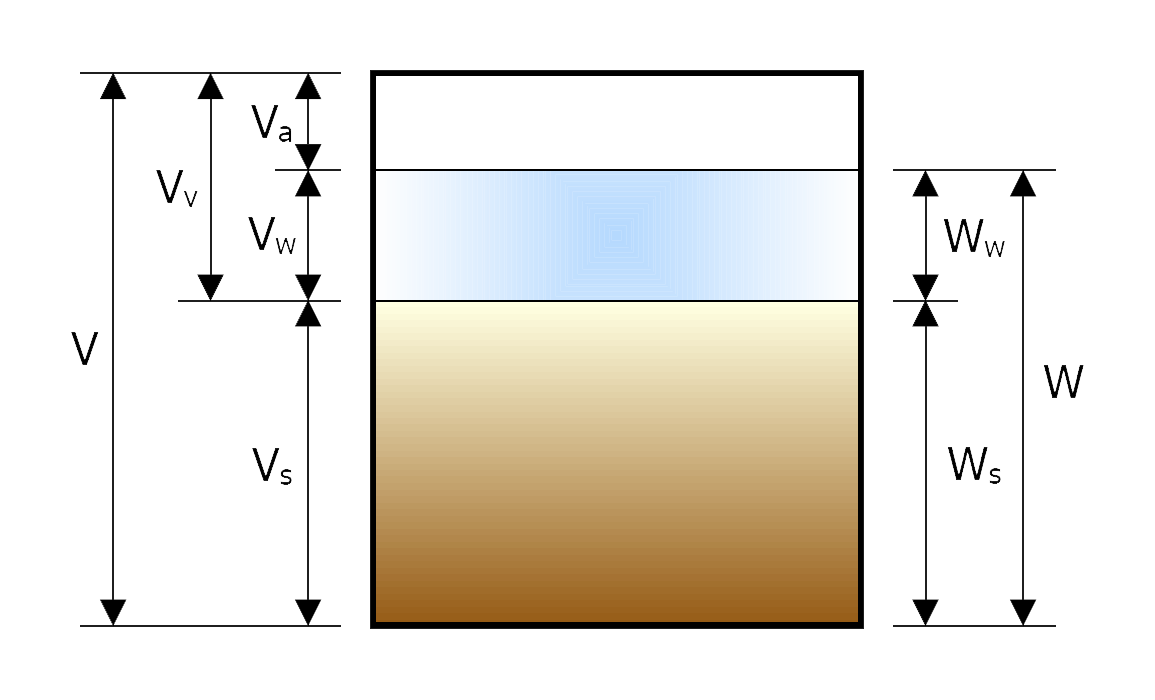

흙덩이 구조에서 첨자 s는 흙 입자, w는 물, a는 공기를 의미한다. 위와 같은 그림을 '''삼상도'''라고 한다.

통일 분류법에 따르면 흙은 입자 크기에 따라 실트, 모래, 자갈로 분류된다. 실트는 0.002mm~0.075mm, 모래는 0.075mm~4.75mm, 자갈은 4.75mm~100mm 크기이다. 이보다 큰 입자는 자갈돌(Cobbles)과 암괴(Boulders)라고 한다.^[1]^[2]

실트와 모래는 주로 석영으로 구성되는데, 이는 석영이 다른 광물보다 풍화에 강하기 때문이다. 운모와 장석도 실트와 모래에서 흔히 발견된다.^[1] 자갈은 모암(母巖)과 유사한 광물 조성을 가진다. 점토 광물은 몬모릴로나이트, 일라이트, 카올리나이트 등이 있으며, 판 모양의 구조와 넓은 비표면적(단위 질량당 표면적)을 가진다. 점토 광물의 비표면적은 1g당 10m²~1000m²에 달하며, 이 때문에 화학적, 정전기적, 반데르발스 상호 작용에 민감하다.^[1]^[3]

흙을 구성하는 주요 광물들은 산소, 규소, 수소, 알루미늄 원자들이 다양한 결정 형태로 결합하여 만들어진다. 칼슘, 나트륨, 칼륨, 마그네슘, 탄소 등도 흙 고체 질량의 상당 부분을 차지한다.^[1]

토양층의 예. a) 표토 및 충적토 b) 성숙한 풍화잔류토 c) 젊은 풍화잔류토 d) 풍화된 암석

2. 1. 흙의 생성

흙은 암석의 풍화작용을 통해 생성된다. 풍화에는 물리적 풍화, 화학적 풍화, 생물학적 풍화가 있다.^[1]^[2]^[3] 발굴, 폭파, 폐기물 처리와 같은 인간 활동도 흙을 만들 수 있다. 지질학적 시간이 지나면서 깊이 묻힌 흙은 압력과 온도에 의해 변성암이나 퇴적암으로 변하고, 녹아서 다시 굳으면 화성암이 되어 순환한다.^[3]

물리적 풍화에는 온도 변화, 균열 속 물의 동결과 융해, 비, 바람, 충격 등이 있다. 화학적 풍화는 암석을 이루는 물질이 용해되어 다른 광물 형태로 침전되는 것이다. 예를 들어 점토 광물은 화성암에 가장 많은 장석의 풍화 작용으로 만들어진다.

실트와 모래의 가장 흔한 광물은 석영(이산화규소)인데, 장석보다 용해가 덜 되기 때문에 흙에 더 많이 존재한다.

실트, 모래, 자갈은 기본적으로 부서진 암석 조각이다.

통일 분류법에 따르면 입자 크기는 다음과 같다.

종류	입자 크기
실트	0.002 mm ~ 0.075 mm
모래	0.075 mm ~ 4.75 mm
자갈	4.75 mm ~ 100 mm

자갈보다 큰 입자는 자갈돌(Cobbles)과 암괴(Boulders)라고 한다.^[1]^[2]

2. 2. 흙의 운반

흙은 중력, 빙하, 물, 바람 등에 의해 운반되며, 운반 방식에 따라 흙의 위치와 입자 모양이 달라진다. 운반되지 않고 원래 생성된 암석과 같은 위치에 존재하는 흙을 잔류토라고 하며, 풍화된 화강암이 대표적인 예이다.^[1]^[2] 운반된 흙에는 다음과 같은 종류가 있다.

충적토: 중력에 의해 산 정상에서 아래로 운반되어 쌓인 흙과 자갈 더미이다.^[1]^[2] 신선하게 파쇄된 충적토 입자는 매우 각진 모양을 띠는 경우가 많다. 반면 강바닥에서 저속으로 연마된 입자는 둥근 모양을 가진다.
물에 의해 운반된 흙: 물의 속도에 따라 입자 크기가 달라지며, 크기별로 등급이 매겨진다. 미사(실트)와 점토는 호수에 침전될 수 있으며, 자갈과 모래는 강바닥에 모인다.
풍성 토양 (바람에 의해 운반된 흙): 입자 크기에 따라 분류되는 경향이 있으며, 사구사(모래 언덕)와 뢰스 등이 있다.^[1]^[2]
빙하에 의해 운반된 흙: 빙하는 큰 암석, 자갈뿐만 아니라 흙까지 운반할 수 있을 만큼 강력하다. 녹는 얼음에 의해 떨어지는 흙은 다양한 입자 크기가 잘 섞여 있을 수 있다.^[1]^[2]

2. 3. 흙의 구성 요소

흙은 흙 입자, 물, 그리고 공기로 구성된다. 흙 입자는 여러 종류의 광물로 이루어져 있다. 물과 공기는 흙 입자 사이의 공간, 즉 '공극' 또는 '간극'을 채운다.^[1]

통일 분류법에 따르면 실트, 모래, 자갈은 크기에 따라 구분된다. 실트 입자는 0.002 mm ~ 0.075 mm, 모래 입자는 0.075 mm ~ 4.75 mm, 자갈 입자는 4.75 mm ~ 100 mm 범위이다. 이보다 더 큰 입자는 자갈돌(Cobbles)과 암괴(Boulders)라고 한다.^[1]^[2]

실트, 모래, 자갈은 다양한 광물로 구성될 수 있는데, 석영은 모래와 실트의 주성분이다. 석영은 다른 암석 광물에 비해 안정성이 높기 때문이다. 운모와 장석도 모래와 실트에서 흔히 발견되는 광물이다.^[1] 자갈은 모암(母巖)과 유사한 광물 조성을 보일 수 있다.

점토 광물은 몬모릴로나이트, 일라이트, 카올리나이트 등이 대표적이다. 이들은 판 모양의 구조를 가지며, 비표면적(단위 질량당 표면적)이 매우 크다. 점토 광물의 비표면적은 보통 1g당 10~1,000 제곱미터에 이른다.^[3] 이러한 큰 비표면적 때문에 점토 광물은 화학적, 정전기적, 반데르발스 상호 작용에 민감하게 반응한다.^[1]

흙을 이루는 광물들은 주로 산소, 규소, 수소, 알루미늄 원자들이 다양한 결정 형태로 결합하여 만들어진다. 칼슘, 나트륨, 칼륨, 마그네슘, 탄소 등도 흙 고체 질량의 상당 부분을 차지한다.^[1]

3. 흙의 분류

흙은 다양한 크기의 입자들로 구성되어 있으며, 이 입자 크기는 흙의 거동을 결정하는 중요한 요소이다. 따라서 흙을 분류할 때 입자 크기를 고려하는 것은 매우 중요하다.

흙의 입도 분포는 흙 입자의 크기 분포를 나타내는 것으로, 체 분석이나 비중계 분석과 같은 방법을 통해 측정할 수 있다. 최근에는 광회절, 산란, 영상 이미징 등 다양한 원리를 이용한 입도 분포 측정 장치를 사용하기도 한다.^[2]

흙을 분류하는 방법 중 하나는 미국 통일분류법(USCS)이다. 이 방법은 흙을 조립토(자갈, 모래)와 세립토(실트, 점토)로 나누고, 입도 분포, 아테르베르크 한계 등을 기준으로 세분한다. 아테르베르크 한계는 흙의 함수비에 따른 상태 변화를 나타내는 지표이며, 소성지수(PI)는 흙의 투수성, 압축성, 전단강도 등과 관련이 있다.^[4]^[10]

통일분류법(USCS)에 따르면, 실트와 점토는 소성지수와 액성한계 값을 소성도표에 도시하여 분류한다. A선은 점토와 실트를 구분하고, 액성한계(LL) 50%는 고소성토와 저소성토를 구분한다. 예를 들어, A선 위에 도시되고 LL>50%인 토양은 CH로 분류된다. 아테르베르크 한계가 그래프의 원점 근처 "빗금 친" 영역에 도시되는 경우, 토양은 'CL-ML'의 이중 분류를 받는다.

일본에서는 미국 통일분류법을 바탕으로 일본의 토질에 맞게 수정된 일본 통일토질분류법(지반공학회 기준: JGS 0051)을 사용한다.^[33]

흙의 입경이 75µm 미만인 실트와 점토는 세립분, 75µm 이상인 모래와 자갈은 조립분이라고 한다. 전체 흙 중량 중 세립분이 차지하는 중량 백분율을 세립분 함유율( $F_c$ )로 나타낸다. 세립분 함유율은 흙을 구분하거나 점성 등 공학적 특성을 추정하고, 지진 발생 시 지반이 액상화되는지 여부를 판단하는 데 사용된다.^[33]

3. 1. 입도 분포

흙은 크기, 모양, 광물학적 조성이 다른 입자들의 혼합물이며, 입자 크기는 흙의 거동에 큰 영향을 미치기 때문에 흙을 분류하는 중요한 기준이 된다. 입도 분포는 다양한 크기의 입자가 상대적으로 얼마나 섞여 있는지를 나타낸다. 보통 누적 분포 그래프를 사용하여 입도를 시각화하는데, 예를 들어 특정 크기보다 작은 입자의 비율을 크기에 따라 나타내는 방식이다.^[2] 중앙 입도(

D_{50}

)는 입자 질량의 50%가 더 미세한 입자로 구성되는 크기를 의미한다. 흙의 투수계수는 작은 입자에 의해 결정되는 경향이 있어, 유효 크기(

D_{10}

)는 입자 질량의 10%가 더 미세한 입자로 구성되는 크기로 정의된다.^[2]

입자 크기가 넓은 범위에 걸쳐 고르게 분포하는 모래와 자갈은 '잘 분급된' 흙이라고 한다. 반면, 흙 입자가 비교적 좁은 크기 범위에 몰려 있는 경우는 '균등하게 분급된' 흙이라고 한다. 흙 시료에 입도 곡선에 뚜렷한 간격이 있다면 (예: 거친 모래가 없는 자갈과 미세 모래의 혼합물) '간극 분급된' 흙일 수 있다. '균등하게 분급된' 흙과 '간극 분급된' 흙은 모두 '불량하게 분급된' 흙으로 간주된다.^[2]

입도 분포를 측정하는 전통적인 방법으로는 체 분석과 비중계 분석이 있다.^[2] 최근에는 체가름법을 빠르게 대체하기 위해 광회절, 산란, 영상 이미징 등 다양한 원리를 이용한 입도 분포 측정 장치를 사용하기도 한다.

일본에서는 흙의 입도 분포 특성을 나타내는 지표로 균등계수(

U_C

)와 곡률계수(

{U_C}'

)를 사용한다.^[33]

균등계수: $U_C=\frac{D_{60}}{D_{10}}$
곡률계수: $U_C'=\frac{(D_{30})^2}{D_{10}{\times}D_{60}}$
$D_{10}$ : 10% 통과 입경
$D_{30}$ : 30% 통과 입경
$D_{60}$ : 60% 통과 입경

균등계수(

U_C

)는 입도 누가곡선의 기울기를 나타내는 지표로, 값이 클수록 입도 분포 폭이 넓다는 것을 의미한다. 과거에는

U_C

가 4~5 이하인 흙을 "입도 분포가 불량한" 흙,

U_C

≧ 10인 흙을 "입도 분포가 양호한" 흙으로 표시했다. 2000년 지반공학회 기준 개정(JGS0051-2000)에 따라 세립분 함유율이 5% 미만인 흙에 대해

U_C

≧ 10일 때 "입경 폭이 넓은",

U_C

< 10일 때 "선별된" 흙으로 부르게 되었다.^[33]

흙의 입경이 75µm 미만인 실트와 점토는 세립분, 75µm 이상인 모래와 자갈은 조립분이라고 한다. 전체 흙 중량 중 세립분이 차지하는 중량 백분율을 세립분 함유율(

F_c

)로 나타낸다. 세립분 함유율은 흙을 구분하거나 점성 등 공학적 특성을 추정하고, 지진 발생 시 지반이 액상화되는지 여부를 판단하는 데 사용된다.^[33]

3. 2. 공학적 분류

미국 통일분류법(USCS)은 흙을 조립토(자갈, 모래)와 세립토(실트, 점토)로 분류하고, 입도 분포, 아테르베르크 한계 등을 기준으로 세분한다. 아테르베르크 한계는 흙의 함수비에 따른 상태 변화를 나타내는 지표로, 액성한계(LL), 소성한계(PL), 수축한계(SL) 등이 있다. 소성지수(PI)는 액성한계와 소성한계의 차이로, 흙의 투수성, 압축성, 전단강도 등과 관련이 있다.^[4]^[10]

통일분류법(USCS)에 따르면, 실트와 점토는 소성지수와 액성한계 값을 소성도표에 도시하여 분류한다. 도표의 A선은 점토(USCS 기호 ''C'')와 실트(기호 ''M'')를 구분한다. 액성한계(LL) 50%는 고소성토(수식 기호 ''H'')와 저소성토(수식 기호 ''L'')를 구분한다. 예를 들어, A선 위에 도시되고 LL>50%인 토양은 ''CH''로 분류된다. 실트와 점토의 다른 분류로는 ''ML'', ''CL'' 및 ''MH''가 있다. 아테르베르크 한계가 그래프의 원점 근처 "빗금 친" 영역에 도시되는 경우, 토양은 'CL-ML'의 이중 분류를 받는다.

특정 입경을 가진 토입자의 혼합 비율을 '''입도'''라고 하며, 일반적으로 '''체가름 시험'''을 통해 얻어진 중량비로 나타낸다. 토질 재료 중 입경이 75µm 미만인 실트와 점토를 세립분, 75µm 이상인 사분과 역분을 조립분이라고 한다. 전체 토질 중량 중 세립분이 차지하는 중량 백분율을 세립분 함유율

F_c

로 나타낸다.

분류법의 예로는 '''미국의 통일분류법'''이 있다.

미국의 통일분류법
74µm 체 통과량 50% 이하: 조립토	4760µm 체 통과량 50% 이하: 자갈(G)	74µm 체 통과량 5% 이하, 비소성	U_c>4, U'_c=1-3 GW 그 외 GP
		74µm 체 통과량 5-12%, 0<I_p<5	GW-GM GP-GM
		74µm 체 통과량 5-12%	GW-GC GP-GC
		74µm 체 통과량 12-49%	GM GC
	4760µm 체 통과량 50% 이상: 모래(S)	74µm 체 통과량 5% 이하, 비소성	U_c>6, U'_c=1-3 SW 그 외 SP
		74µm 체 통과량 5-12%, 0<I_p<5	SW-SM SP-SM
		74µm 체 통과량 5-12%	SW-SC SP-SC
		74µm 체 통과량 12-49%	SM SC
74µm 체 통과량 50% 이상: 세립토	A선 이하: 실트(M)	w_L≧50 MH w_L<50 ML
	A선 이상: 점토(C)	w_L≧50 CH w_L<50 CL
	유기질토(O)	w_L≧50 OH w_L<50 OL
매우 유기질인 토: 피트(Pt)

위의 분류를 기반으로 일본의 토질에 맞는 '''일본 통일토질분류법'''(지반공학회 기준: JGS 0051)이 정해졌다.^[33]

4. 흙의 삼상 관계

토질역학에서 흙은 물, 공기, 흙 입자 세 가지로 이루어져 있다고 보며, 이 세 가지를 흙의 삼상(三相)이라고 한다. 이들의 비율에 따라 흙의 역학적 특성이 달라진다. 물과 공기가 차지하는 부분은 '공극' 또는 '간극'이라고도 한다.^[34]

흙은 토립자(soil particles), 물(water), 공기(air)의 3상으로 구성되어 있으며, 물과 공기의 두 상을 합쳐 간극(void, 첨자: ''v'')이라고 한다.

흙의 삼상과 관련된 물리량은 다음과 같다.

'''간극비''' ('''Void ratio''') : ''e'' = ''V_v''/''V_s''
'''간극률''' ('''Porosity''') : ''n'' = ''V_v''/''V''
'''포화도''' ('''Degree of Saturation''') : ''S_r'' = ''V_w''/''V_v''×100 (%)
'''함수비''' ('''Water content''') : ''w'' = ''W_w''/''W_s''×100 (%)
'''체적함수비''' ('''Water content by volume''') : ''θ'' = ''V_w''/''V''×100 (%)
'''토립자의 밀도'''
'''토립자의 비중'''
'''상대 밀도''' ('''Relative density''')

이 외에도 흙과 관련된 물리량은 다음과 같다.

'''민감도''' ('''Sensitivity ratio''') : ''S_t'' = 교란되지 않은 흙의 일축압축강도 / 교란된 흙의 일축압축강도
'''소성지수''' ('''Plasticity index''') : ''I_p'' = ''w_L'' - ''w_p''
'''액성지수''' ('''Liquidity index''') : ''I_L'' = (''w'' - ''w_p'') / ''I_p''
'''점착지수''' ('''Consistency index''') : ''I_c'' = (''w_L'' - ''w'') / ''I_p''

삼상도에서 V_s = 1이라고 볼 경우, 삼상도의 각 요소들은 다음과 같이 요약할 수 있다.^[34]

$V_w = \frac{S\cdot e}{100}$
$V_v = e$
V = 1 + e
$W_s = G_s \gamma_w$
$W_w = \frac{S\cdot e}{100} \gamma_w$
$\left( G_s + \frac{S\cdot e}{100} \right) \gamma_w$

4. 1. 공극비 (e)

흙 입자의 부피에 대한 간극(물과 공기의 부피)의 비를 간극비라고 한다.^[34]

:

e = \frac{V_v}{V_s}

여기서,

''V_v''는 간극의 부피
''V_s''는 흙 입자의 부피이다.

:

G_s \omega = S e

4. 2. 공극률 (n)

공극률(n)은 흙 전체의 부피 V에 대한 공극만의 부피 V_v의 비를 백분율(%)로 나타낸 것이다. 식으로 표현하면 다음과 같다.^[34]

:

n = \frac{V_v}{V}\times 100 (\%)

흙은 토립자(soil particles), 물(water), 공기(air)의 3상으로 구성되어 있으며, 물과 공기를 합쳐 간극(void)이라고 한다. 간극비(e)는 흙 고체 부분 부피(''V_s'')에 대한 간극 부분 부피(''V_v'')의 비를 나타낸다.

4. 3. 포화도 (S)

포화도(Degree of Saturation, S)는 흙에서 공극(빈 공간) 부피에 대한 물의 부피 비를 나타내며, 다음과 같이 정의된다.^[34]

:

S = \frac{V_w}{V_v}\times 100 (\%)

:

G_s \omega = S e

여기서,

V_w는 물이 차지하는 부피
V_v는 공극의 부피
G_s는 흙 입자의 비중
ω는 함수비
e는 간극비

이다.

4. 4. 함수비 (ω)

함수비(ω)는 흙 입자 중량 W_s와 물의 중량 W_w를 이용해 다음과 같이 정의한다.^[34]

:

\omega = \frac{W_w}{W_s}\times 100 (\%)

함수비는 다짐에 영향을 미치며, 가장 다짐 효율이 좋은 함수비를 '''최적 함수비'''라고 부른다.

4. 5. 진비중 (G_s)

흙의 진비중 G_s는 흙의 입자 단위중량 γ_s(또는 입자 밀도 ρ_s)와 4°C 물의 단위중량 γ_w(또는 물 밀도 ρ_w)를 이용해 다음과 같이 정의한다. 그냥 비중이라고 하기도 한다.

:

G_s = \frac{\gamma_s}{\gamma_w} = \frac{\rho_s g}{\rho_w g} = \frac{\rho_s}{\rho_w}

4. 6. 단위중량 (γ)

흙 시료에 물이 포함되었는지, 수중에 흙 시료가 있는지 등 상황에 따라 단위중량은 여러 가지로 정의된다.

; 전체단위중량(total unit weight), 또는 습윤단위중량(moist unit weight)

:

\gamma_t = \frac{W}{V} = \frac{W_s + W_w}{V} = \frac{W_s (1 + W_w/W_s)}{V} = \frac{W_s (1+\omega)}{V} = \frac{G_s + Se}{1+e} \gamma_w

: 공기 중에 있는 습윤 상태의 흙 시료 단위중량을 전체단위중량 또는 습윤단위중량이라고 한다.^[1]

; 건조단위중량(dry unit weight)

:

\gamma_d = \frac{W_s}{V} = \frac{G_s \gamma_w}{1+e} = \frac{\gamma_t}{1+\omega}

: 건조되어 물이 없는 경우의 흙 시료 단위중량을 건조단위중량이라고 한다.^[1]

; 포화단위중량(saturated unit weight)

:

\gamma_{sat} = \frac{W}{V} = \frac{W_s + W_w}{V} = \frac{G_s \gamma_w + \omega G_s \gamma_w}{1+e} = \frac{G_s \gamma_w + S e \gamma_w}{1+e} = \frac{G_s + e}{1+e}\gamma_w

: 공극이 모두 물로 채워져 있을 때 단위중량을 포화단위중량이라고 한다.^[2]

; 수중단위중량(submerged unit weight)

:

\gamma_{sub} = \gamma_{sat} - \gamma_w = \frac{G_s + e}{1+e}\gamma_w - \gamma_w = \frac{G_s - 1}{1+e}\gamma_w

: 지하수위 아래에 있는 흙의 단위중량을 수중단위중량이라고 한다. 지하수위 아래에 있는 흙은 부력을 받기 때문에, 포화단위중량보다 가벼워져야 하므로 포화단위중량에서 물의 단위중량을 빼준다.^[2]

4. 7. 상대 밀도 (D_r)

상대 밀도(영어: Relative density, D_r)는 사질토의 다짐 정도를 나타내는 지표이다.^[35] 상대 밀도는 최대 공극비(

e_{max}

), 최소 공극비(

e_{min}

), 현재 공극비(e)를 이용하여 계산한다.

:

D_r=\frac{e_{max}-e}{e_{max}-e_{min}}\times 100(\%)

:

D_r=\frac{\gamma_{dmax}}{\gamma_d}\cdot \frac{\gamma_d-\gamma_{dmin}}{\gamma_{dmax}-\gamma_{dmin}}\times 100(\%)

$e_{max}$ : 최대 공극비
$e_{min}$ : 최소 공극비
e : 공극비
$\gamma_{dmax}$ : 최대 건조 단위중량
$\gamma_{dmin}$ : 최소 건조 단위중량
$\gamma_d$ : 건조 단위중량

상대 밀도를 계산하는 방법은 ASTM D4254-00(2006)에 정의되어 있다.^[12]

만약 D_r = 100%이면 모래 또는 자갈은 매우 조밀한 상태이고, D_r = 0%이면 흙은 매우 느슨하고 불안정한 상태이다.

5. 흙의 투수성

흙의 투수성은 물이 흙 속을 통과하는 정도를 나타내는 성질이다. 흙은 다양한 크기의 입자와 그 사이의 공극으로 이루어져 있는데, 이 공극을 통해 물이 흐르게 된다.

투수성은 다르시 법칙으로 설명된다. 다르시 법칙은 흙 속의 물의 흐름이 수리구배에 비례한다는 것을 나타낸다. 수리구배는 물의 높이 차이(전수두)를 거리로 나눈 값으로, 물이 얼마나 빠르게 흐르는지를 결정하는 중요한 요인이다.

투수성을 나타내는 값은 수리전도도( $k$ )이며, 흙의 종류에 따라 큰 차이를 보인다. 예를 들어, 점토는 매우 작은 투수계수( $10^{-12}\frac{m}{s}$ 정도)를 가지는 반면, 자갈은 큰 투수계수( $10^{-1}\frac{m}{s}$ 정도)를 가진다.

흙의 투수성은 층상 구조, 이질성 등에 영향을 받기 때문에 정확하게 측정하기 어렵다.^[4]

5. 1. 다르시 법칙

다르시 법칙은 다공성 매질을 통한 간극 유체의 단위 시간당 유량이 과잉 유체압의 거리에 따른 변화율에 비례한다는 법칙이다.^[4]^[6]^[20] 비례 상수에는 유체의 점성과 토양의 절대 투수계수가 포함된다.

토양이 채워진 수평 관을 이용한 간단한 실험에서, 총 유출량

Q

(단위 시간당 부피, 예: ft³/s 또는 m³/s)은 절대 투수계수

K

, 단면적

A

및 거리에 따른 간극압 변화율

\frac{u_b-u_a}{L}

에 비례하고 유체의 동점성계수

\mu

에 반비례한다.

:

Q=\frac{-K A}{\mu}\frac{(u_b-u_a)}{L}

토목기사는 주로 물과 지구(지구 중력)에서 발생하는 문제를 다룬다. 이러한 문제에 대해 토목기사는 다르시 법칙을 다음과 같이 더 간단한 형태로 작성한다.^[4]^[6]^[20]

:

v = k i

여기서

k

는 수리전도도(

k = \frac {K \rho_w g} {\mu_w}

)이고,

i

는 수리구배로 거리에 따른 전수두의 변화율을 의미한다.

다르시 법칙은 1차원, 2차원, 3차원 모두에 적용된다.^[3] 2차원 또는 3차원에서 정상 상태의 침투는 라플라스 방정식으로 설명된다. 전통적으로 2차원 침투 문제는 흐름망을 이용하여 해결했다.^[3]^[20]^[15] 흐름망은 물의 흐름 방향을 나타내는 흐름선과 일정한 전체 수두 방향을 나타내는 등전위선으로 구성된다. 흐름망은 댐과 차수벽 아래의 침투량을 추정하는 데 사용될 수 있다.

토양은 종류에 따라 투수성이 크게 다르다. 자세한 내용은 투수성 항목을 참조한다.

5. 2. 침투력과 침식

침투 속도가 충분히 클 경우, 흙 입자에 가해지는 마찰 항력으로 인해 침식이 발생할 수 있다. 수직 상향 침투는 차수벽 하류 측과 댐 또는 제방의 토대 아래에서 위험의 원인이 된다. "토사 파이핑(soil piping)"으로 알려진 토양 침식은 구조물의 붕괴와 싱크홀 형성으로 이어질 수 있다.^[16] 침투수는 침투의 출구점부터 토양을 제거하고, 침식은 상류 쪽으로 진행된다.^[17] 활동적인 토사 파이프의 배출 끝 부분의 모양을 설명하기 위해 "샌드 보일(sand boil)"이라는 용어가 사용된다.^[17]

5. 3. 침투압

상향으로의 침투는 토양 내 유효응력을 감소시켜 흙의 강도를 약화시킨다. 토양 내 한 지점에서의 수압이 그 지점에서의 총 수직응력과 같을 때, 유효응력은 0이 되고 토양은 변형에 대한 마찰 저항력이 없어진다. 지표면 층의 경우, 상향 수리구배가 임계구배와 같을 때 층 내에서 수직 유효응력이 0이 된다.^[20] 유효응력이 0일 때 토양은 매우 적은 강도를 가지며, 상대적으로 불투수성인 토양 층은 하부의 수압으로 인해 융기될 수 있다. 상향 침투로 인한 강도 손실은 제방 붕괴의 일반적인 원인이다. 상향 침투와 관련된 유효응력 0의 상태는 액상화, 퀵샌드, 또는 비등 상태라고도 한다. 퀵샌드는 토양 입자가 움직여 '살아있는' 것처럼 보이기 때문에(성경적 의미에서의 '살아있는' – '죽은' 것과 반대) 그렇게 명명되었다. (퀵샌드에 '빨려 들어갈' 수는 없다는 점에 유의해야 한다. 반대로, 신체의 약 절반이 물 밖으로 나온 상태로 떠 있을 것이다.)^[18]

6. 유효응력과 모관 현상

토질 역학을 이해하려면 흙을 구성하는 여러 요소들이 수직 응력과 전단 응력을 어떻게 나누어 받는지 알아야 한다. 기체나 액체는 전단응력에 거의 저항하지 않는다. 흙의 전단 저항은 입자 사이의 마찰과 맞물림으로 발생하며, 마찰은 고체 입자 간 접촉 응력에 따라 달라진다. 반면 수직 응력은 유체와 입자가 함께 받는다. 흙 입자 사이의 빈 공간인 공극 속 공기는 압축성이 매우 커서 대부분의 지반 공학 문제에서 수직 응력을 거의 받지 않는다. 그러나 물은 비압축성이므로, 공극이 물로 가득 차 있으면(포화) 입자들을 더 가깝게 만들기 위해 공극에서 물을 짜내야 한다.

칼 테르차기(Karl Terzaghi)는 유효응력 원리를 제안했는데, 유효응력 ''σ''' (고체 입자 사이의 평균 응력)은 전체 응력에서 공극압(간극수압)을 빼서 계산할 수 있다는 것이다.

:

\sigma' = \sigma - u\,

여기서 ''σ''는 전체 응력, ''u''는 공극압(간극수압)이다. 실제로는 ''σ'''를 직접 측정하기 어려우므로, 공극압과 수직 전체 응력으로부터 수직 유효응력을 계산한다. 압력과 응력은 다른 개념으로, 압력은 모든 방향에서 같지만, 응력은 방향에 따라 다를 수 있다. 토질역학에서는 압축 응력과 압력을 양수로, 인장 응력을 음수로 정의한다.

6. 1. 유효응력

칼 테르차기가 제안한 유효응력 원리에 따르면, 유효응력 ''σ''' (흙 입자 간 평균 응력)는 전체 응력에서 간극수압을 빼서 계산할 수 있다.

:

\sigma' = \sigma - u\,

여기서 ''σ''는 전체 응력이고, ''u''는 간극수압이다. 유효응력 ''σ'''를 직접 측정하는 것은 어렵기 때문에, 실제로는 간극수압과 수직 전체 응력으로부터 수직 유효응력을 계산한다. 압력과 응력의 차이도 중요한데, 압력은 모든 방향에서 같지만, 응력은 방향에 따라 다를 수 있다. 토질역학에서는 압축 응력과 압력을 양수로, 인장 응력을 음수로 간주한다.

평지 조건에서 어떤 지점의 총 수직 응력(σv)은 평균적으로 그 지점 위 모든 것의 단위 면적당 무게이다. 밀도(ρ)이고 두께(H)인 균일한 표면층 아래의 수직 응력은 다음과 같다.

:σv = ρgH = γH

여기서 g는 중력 가속도이고, γ는 상재층의 단위 중량이다. 여러 층의 토양이나 물이 있는 경우, 총 수직 응력은 각 층의 단위 중량과 두께의 곱을 모두 더하여 계산할 수 있다. 총 응력은 상재 토양의 밀도에 비례하여 깊이가 깊어질수록 증가한다.

이러한 방법으로 수평 총 응력을 계산하는 것은 불가능하며, 측압은 다른 곳에서 다룬다.

6. 2. 간극수압

간극수압은 흙 속의 물이 받는 압력이다. 칼 테르차기는 유효응력 원리를 제안했는데, 유효응력 ''σ''' (고체 입자 사이의 평균 입자 간 응력)는 전체 응력에서 공극압을 빼서 계산할 수 있다는 것이다.

:

\sigma' = \sigma - u\,

여기서 ''σ''는 전체 응력이고, ''u''는 공극압이다. ''σ'''를 직접 측정하기는 어렵기 때문에, 실제로는 공극압과 수직 전체 응력으로부터 수직 유효응력을 계산한다. 압력과 응력은 다른 개념이다. 정의에 따르면, 한 점에서의 압력은 모든 방향에서 같지만, 한 점에서의 응력은 방향에 따라 다를 수 있다. 토질역학에서는 압축 응력과 압력을 양수로, 인장 응력을 음수로 간주하는데, 이는 응력에 대한 고체역학의 부호 규약과 다르다.

토질의 역학을 이해하려면 여러 상(phase)이 어떻게 수직응력과 전단응력을 분담하는지 이해해야 한다. 기체나 액체는 전단응력에 대한 저항을 거의 제공하지 않는다. 토양의 전단저항은 입자의 마찰과 상호 맞물림에 의해 제공되며, 마찰은 고체 입자 사이의 입자 간 접촉 응력에 따라 달라진다. 반면에 수직응력은 유체와 입자가 분담한다. 공극 공기는 비교적 압축성이 높기 때문에 대부분의 지반 공학 문제에서 수직응력을 거의 받지 않지만, 액체 상태의 물은 비교적 비압축성이므로 공극이 물로 포화되어 있으면 입자를 더 가까이 밀집시키기 위해 공극수를 짜내야 한다.

6. 3. 모관 현상

모관 현상은 물의 표면 장력 때문에 지하수면 위로 물이 상승하는 현상이다. 모세관 현상에 의해 물은 좁은 관을 따라 올라간다. 이와 유사하게, 흙 입자 사이의 작은 공극으로도 지하수면 위로 물이 상승할 수 있다. 실제로 흙은 지하수면 위 일정 높이까지 완전히 포화될 수 있다. 모세관 포화 높이 위에서는 흙이 습할 수 있지만, 수분 함량은 높이에 따라 감소한다. 모세관대의 물이 이동하지 않는다면, 수압은 정수압 평형 방정식(

u = \rho_w g z_w

)을 따른다. 여기서

z_w

는 지하수면 위에서는 음수이므로, 지하수면 위에서는 정수압이 음수이다. 모세관 포화대의 두께는 공극 크기에 따라 달라지는데, 일반적으로 고운 모래에서는 몇 센티미터, 미사나 점토에서는 수십 미터까지 다양하다.^[3] 점토 토양의 경우 평균 선형 크기 L=0.15 mm, D=2.7인 균일하게 분포된 D차원 프랙탈의 집합으로 공극 공간이 구성되어 있다.^[19]

물의 표면 장력은 축축한 모래성이나 젖은 점토 덩어리에서 물이 빠져나가지 않는 이유를 설명한다. 음의 수압은 물이 입자에 달라붙고 입자들을 서로 끌어당기게 하며, 입자 접촉면의 마찰력은 모래성을 안정적으로 만든다. 젖은 모래성이 자유 수면 아래로 잠기는 순간, 음의 압력이 사라지고 모래성은 무너진다. 유효응력 방정식(

\sigma' = \sigma - u,

)을 고려하면, 수압이 음수이면, 자유 표면(전체 수직 응력이 0인 표면)에서도 유효응력이 양수일 수 있다. 음의 공극수압은 입자들을 서로 끌어당겨 입자 간 압축 접촉력을 발생시킨다.

점토 토양의 음의 공극수압은 모래보다 훨씬 강력할 수 있다. 음의 공극수압은 점토 토양이 건조될 때 수축하고 습윤될 때 팽윤하는 이유를 설명한다. 이러한 팽윤과 수축은 특히 경량 구조물과 도로에 심각한 손상을 야기할 수 있다.^[20]

7. 흙의 압밀

압밀은 흙에 응력이 가해져 흙 입자가 더욱 조밀하게 뭉쳐지고, 간극수가 빠져나가면서 체적이 감소하는 현상이다. 흙은 다짐을 통해 더 강하고 단단해질 수 있다. 토목 구조물 건설 시 충분한 다짐이 이루어져야 하지만, 다짐 효율은 방법과 흙의 함수비에 따라 크게 달라진다. 가장 다짐 효율이 좋은 함수비를 '''최적 함수비(W optimum)'''라고 한다.

7. 1. 압밀 이론

압밀(Consolidation)은 흙에 응력이 가해져 흙 입자가 더욱 조밀하게 뭉쳐짐으로써 부피가 감소하는 과정이다. 물로 포화된 흙에서 이 현상이 발생하면 물이 흙에서 짜여 나온다. 두꺼운 점토층에서 물을 짜내는 데는 수년이 걸릴 수 있지만, 모래층에서는 수초 만에 물이 짜여 나올 수 있다. 건물 기초 또는 새로운 제방을 건설하면 아래쪽 흙이 압밀되어 침하가 발생하고, 이는 건물이나 제방에 손상을 줄 수 있다. 칼 테르자기(Karl Terzaghi)는 1차원 압밀 이론을 개발하여 침하량과 침하 발생 시간을 예측할 수 있게 하였다.^[21] 이후 모리스 비오(Maurice Biot)는 3차원 토양 압밀 이론을 개발하여 테르자기의 1차원 모델을 더 일반적인 가설로 확장하고, 다공질탄성체의 기본 방정식 집합을 도입하였다. 압밀 시험을 통해 흙의 압축 지수와 압밀 계수를 결정할 수 있다.

응력이 제거되면 흙은 되튐 현상을 보이며, 물이 공극으로 다시 들어가 압밀 과정에서 손실된 부피의 일부를 회복한다. 응력이 다시 가해지면 흙은 재압밀 곡선을 따라 다시 압밀되며, 이 곡선은 재압밀 지수로 정의된다. 큰 압력으로 압밀된 후 하중이 제거된 흙은 과압밀(overconsolidated)된 것으로 간주된다. 과거 최대 수직 유효 응력은 과압밀 응력(preconsolidation stress)이라고 한다. 현재 과거 최대 수직 유효 응력을 경험하고 있는 흙은 정상 압밀(normally consolidated)되었다고 한다. 과압밀 비(OCR, Overconsolidation Ratio)는 과거 최대 수직 유효 응력과 현재 수직 유효 응력의 비율이다. OCR은 두 가지 이유로 중요한데, 첫째, 정상 압밀 토양의 압축성이 과압밀 토양보다 훨씬 크기 때문이고, 둘째, 점토의 전단 거동과 팽창성은 임계상태 토질역학을 통해 OCR과 관련이 있기 때문이다. 고도로 과압밀된 점토는 팽창성을 나타내는 반면, 정상 압밀 토양은 수축 경향이 있다.^[2]^[3]^[4]

7. 2. 과압밀

과거에 큰 압력을 받아 압밀된 후 하중이 제거된 흙은 과압밀(overconsolidated)된 것으로 간주된다. 과거 최대 수직 유효 응력은 과압밀 응력(preconsolidation stress)이라고 한다. 현재 과거 최대 수직 유효 응력을 경험하고 있는 흙은 정상 압밀(normally consolidated)되었다고 한다. 과압밀 비(OCR, Overconsolidation Ratio)는 과거 최대 수직 유효 응력과 현재 수직 유효 응력의 비율이다. OCR은 두 가지 이유로 중요하다. 첫째, 정상 압밀 흙의 압축성이 과압밀 흙보다 훨씬 크기 때문이고, 둘째, 점토의 전단 거동과 팽창성은 임계상태 토질역학을 통해 OCR과 관련이 있기 때문이다. 고도로 과압밀된 점토는 팽창성을 나타내는 반면, 정상 압밀 토양은 수축 경향이 있다.^[2]^[3]^[4]

8. 흙의 전단 거동

흙의 전단강도와 강성은 흙의 안정성과 변형량을 결정하는 중요한 요소이다. 사면의 안정성, 건물이나 교량의 침하 가능성, 지지벽에 작용하는 압력을 결정하기 위해서는 흙의 전단강도에 대한 이해가 필수적이다.^[20]

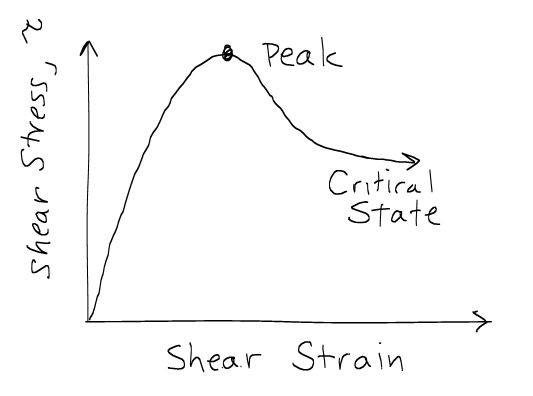
토양 요소의 파괴와 지반 구조물(예: 건물 기초, 사면)의 파괴는 다를 수 있다. 일부 토양 요소는 구조물이 파괴되기 전에 최대 강도에 도달할 수 있다. 응력-변형률 곡선에서 흙 요소의 "전단강도"와 항복점을 정의하는 기준은 다양하다. 응력-변형률 곡선의 최고점을 최대 전단강도로 정의하거나, 전단 저항이 일정해지는 큰 변형률 후의 값을 임계 상태에서의 전단강도로 정의할 수 있다. 시험이 끝나기 전에 응력-변형률 곡선이 안정되지 않으면, 15~20% 변형률에서의 전단 저항을 "강도"로 간주하기도 한다.^[20] 흙의 전단강도는 유효응력, 간극비 등 여러 요인에 따라 달라진다.

전단 강성은 파괴 전 기초와 사면의 변형량 평가에 중요하며, 전단파 속도와 관련이 있다. 전단응력을 전단변형률의 함수로 나타낸 그래프의 초기 기울기를 전단계수라고 한다.

토양의 응력-변형률 관계와 전단강도는 다음과 같은 요인들의 영향을 받는다.^[23]

# 토성(기본적인 토재): 광물학적 조성, 입도 및 입도 분포, 입자 모양, 간극 유체의 종류와 함량, 입자 표면 및 간극 유체 내 이온.

# 상태(초기): 초기 간극비, 유효수직응력 및 전단응력(응력 이력). 상태는 느슨함, 조밀함, 과압밀, 정규압밀, 경도, 연약함, 수축성, 팽창성 등으로 설명될 수 있다.

# 구조: 토괴 내 입자의 배열 방식. 층, 절리, 균열, 광택면, 공극, 포켓, 시멘테이션 등이 구조의 일부이다. 토양의 구조는 원지반, 교란, 재성형, 다짐, 시멘테이션; 플록큘런트, 벌집형, 단립형; 플록큘레이션, 디플록큘레이션; 층상, 엽층상; 등방성 및 이방성 등으로 설명된다.

# 하중 조건: 유효 응력 경로 - 배수, 불배수, 하중의 종류(크기, 속도(정적, 동적)), 시간 이력(단조, 반복).

토는 일반적으로 전단(せん断) 파괴되므로, 토의 강도(強度)는 '''전단강도(せん断強度)'''를 의미한다. 강도 측정에는 주로 '''직접전단시험(一面せん断試験)''', '''삼축압축시험(三軸圧縮試験)''', '''일축압축시험(一軸圧縮試験)'''이 사용된다.

전단시험의 종류는 다음과 같다.

구분	종류
실내 시험
현장 시험

8. 1. 전단강도

흙의 전단강도는 주로 입자 간 마찰력과 입자들의 상호 맞물림(딜라탄시)에 의해 발생한다.^[3]^[11] 딜라탄시는 전단 변형 시 입자들이 서로 멀어지는 현상이다.^[11] 입자가 압축력에 대해 팽창하는 데 필요한 추가 에너지로 인해, 딜레이턴트 토양은 수축성 토양보다 더 큰 최대 강도를 갖는다.

토양이 임계상태에 도달하면 더 이상 수축하거나 팽창하지 않으며, 파괴면의 전단응력 τ_crit은 파괴면의 유효수직응력 σ_n'과 임계상태 마찰각 φ_crit'에 의해 결정된다.

:τ_crit = σ_n' tan φ_crit'

그러나 토양의 최대 강도는 상호 맞물림(팽창) 효과로 인해 더 클 수 있다.

:τ_peak = σ_n' tan φ_peak'

여기서 φ_peak' > φ_crit'이다. 그러나 설계에 임계상태 값보다 큰 마찰각을 사용하는 경우 주의가 필요하다. 최대 강도는 기초, 사면 또는 옹벽과 같은 실제 문제에서 동시에 모든 곳에서 동원되는 것은 아니다. 임계상태 마찰각은 최대 마찰각만큼 변화가 심하지 않으므로 안심하고 사용할 수 있다.^[3]^[4]^[11]

쿨롱은 팽창의 중요성을 인식하지 못하고 토양의 전단강도를 응집력과 마찰력의 조합으로 표현할 수 있다고 제안했다.^[11]

:τ_f = c' + σ_f' tan φ'

현재 마지막 방정식의 c' 및 φ' 매개변수는 기본적인 토양 특성이 아니라는 것이 알려져 있다.^[3]^[6]^[11]^[22] 특히, c'와 φ'는 유효응력의 크기에 따라 달라진다.

8. 2. 배수 조건

흙이 전단될 때 배수 조건은 흙의 거동에 큰 영향을 미친다. 배수 조건은 크게 배수 전단과 비배수 전단으로 나뉜다.

배수 전단: 물이 흙 속으로 자유롭게 이동할 수 있는 조건에서 발생하는 전단이다. 전단 속도가 느려 물의 압력이 무시할 수 있을 정도일 때 발생한다.
비배수 전단: 물의 이동이 제한된 조건에서 발생하는 전단이다. 전단 속도가 빨라 흙 입자 사이 공간의 팽창이나 수축 속도보다 물이 빨려 들어가거나 짜내지는 속도가 더 느릴 때 발생한다.

비배수 전단 시에는 흙의 체적 변화 경향에 따라 간극 수압(u)이 변한다. 유효 응력 방정식(${{\sigma }'=\sigma -u\,}$)에 따라 간극 수압의 변화는 유효 응력에 직접적인 영향을 미치며, 이는 흙의 강도 변화로 이어진다. 따라서 흙이 수축성인지 팽창성인지에 따라 비배수 전단강도는 배수 전단강도보다 작거나 클 수 있다.^[20]

8. 3. 전단 시험

흙의 강도 정수는 실험실에서 직접전단시험, 삼축압축시험, 단순전단시험, 낙추추시험, (수동) 전단날개시험을 이용하여 측정할 수 있으며, 오늘날 실제로 사용되는 이러한 장비의 수많은 다른 장치와 변형이 있다.^[23] 지반 내 토양의 강도와 강성을 특성화하기 위해 수행되는 시험에는 원추관입시험과 표준관입시험이 있다.

전단 시험의 종류는 다음과 같다.

구분	종류
실내 시험
현장 시험

9. 토질역학의 응용

토질역학은 흙의 역학적 특성을 다루는 학문으로, 다양한 분야에 응용된다.

측지압 이론은 흙이 중력에 수직으로 작용하는 응력의 크기를 추정하는 데 사용되며, 옹벽 설계에 중요한 토압을 계산하는 데 활용된다. 토압은 흙의 상태에 따라 정지토압, 수동토압, 능동토압으로 분류된다.

지반은 상부 구조물의 하중을 지탱하는 역할을 한다. 지반의 지지력이 구조물 하중보다 작으면 지반이 붕괴될 수 있으므로, 기초 설계 등을 통해 충분한 지지력을 확보해야 한다. 테르차기의 지지력 공식을 이용하면 얕은 기초의 지지력을 추정할 수 있으며, 폭이 넓고 깊은 기초일수록 더 큰 지지력을 갖는다.^[2]

흙은 전단강도와 점착력을 가지므로 어느 정도 경사를 유지할 수 있지만, 한계를 넘으면 사면붕괴가 발생할 수 있다. 사면의 안전율은 상정한 활동면에서의 전단강도와 발생하는 전단력의 비로 평가된다.

9. 1. 측압

측지압 이론은 흙이 중력에 수직으로 작용할 수 있는 응력의 크기를 추정하는 데 사용된다. 이는 옹벽에 작용하는 응력이다. 측지압 계수 K는 점착력이 없는 토사에 대해 수직 유효 응력에 대한 측면(수평) 유효 응력의 비율로 정의된다(K=σ'_h/σ'_v). 정지, 활동, 수동의 세 가지 계수가 있다. 정지 응력은 어떠한 교란이 발생하기 전 지반 내의 측면 응력이다. 활동 응력 상태는 측면 응력의 영향으로 벽이 토사로부터 멀어질 때 도달하며, 측면 응력 감소로 인한 전단 파괴로 인해 발생한다. 수동 응력 상태는 벽이 토사에 충분히 밀려 측면 응력 증가로 인해 질량 내에서 전단 파괴를 일으킬 때 도달한다. 측지압을 추정하기 위한 많은 이론이 있으며, 일부는 경험적으로 기반을 두고 있고 일부는 해석적으로 유도된다.

토압(Earth Pressure)은 지반 내에서 토사가 작용하는 압력으로, 상태에 따라 '''정지토압''', '''수동토압''', '''능동토압'''으로 분류된다.

9. 2. 지지력

토양의 지지력은 기초와 토양 사이의 평균 접촉 응력으로, 이 응력이 토양의 전단 파괴를 일으키는 값이다. 허용 지지력은 지지력을 안전율로 나눈 값이다. 연약한 지반에서는 하중을 받는 기초 아래에서 실제 전단 파괴가 발생하지 않고 큰 침하가 발생할 수 있는데, 이 경우 허용 지지력은 최대 허용 침하량을 고려하여 결정된다.^[1]

지반 강도 평가는 공사 및 설계 단계에서 중요하다. 설계 및 시공을 위한 지반으로서 토양의 적합성을 결정하는 데에는 캘리포니아 지지력 비율(CBR) 시험이 일반적으로 사용된다. 현장 플레이트 하중 시험은 토양/지반의 변형 및 파괴 특성과 지반 반력 계수(ks)를 예측하는 데 사용되며, 지반 반력 계수(ks)는 기초 설계, 지반-구조물 상호 작용 연구 및 고속도로 포장 설계에 사용된다.^[1]

지반은 상부에 세운 구조물의 하중을 지탱해야 한다. 그러나 그 하중이 지반의 '''지지력'''을 초과하면 지반이 붕괴되므로, 구조물을 기초로 지지하는 등의 조치를 통해 충분한 지지력을 확보해야 한다.^[2]

테르차기의 지지력 공식에 따르면, 폭 ''B'' , 기초깊이 ''D''_f 의 얕은 기초의 지지력 ''q'' 는 다음과 같이 표현된다.

:

q = cN_\mathrm{c} + \frac{1}{2}\gamma_1BN_\gamma + \gamma_2D_\mathrm{f}N_\mathrm{q}

여기서 ''N''_c , ''N''_γ , ''N''_q 는 '''지지력 계수''', ''c'' 는 점착력이다. 일반적으로 폭이 넓고 깊은 기초일수록 더 큰 지지력을 기대할 수 있다.^[2]

9. 3. 사면 안정

thumb

사면 안정 분야는 토석 댐 사면, 기타 제방 사면, 굴착 사면 및 토사 및 연암의 자연 사면의 정적 및 동적 안정성 분석을 포함한다.^[24]

토사 사면에는 절단된 구형 취약대가 발생할 수 있다. 이러한 현상이 발생할 확률은 간단한 2차원 원형 분석 패키지를 사용하여 미리 계산할 수 있다.^[25] 분석의 주요 어려움 중 하나는 특정 상황에 대한 가장 가능성이 높은 활동면을 찾는 것이다.^[26] 많은 산사태는 사후 분석만 이루어졌다. 산사태 대비 암석 강도는 고려해야 할 두 가지 요소이다.

토는 전단강도와 점착력을 가지므로, 어느 정도의 경사를 주어도 자립할 수 있다. 그러나 그 한계를 넘으면 사면붕괴를 일으켜 민가나 인명을 앗아갈 수도 있다.

사면의 안전율은 상정한 활동면에서의 전단강도와 발생하는 전단력의 비로 평가된다.

: 안전율 ''F_s'' = 전단강도 / 전단력

10. 최근 동향 (DSSM)

동역학계 기반 토질역학(DSSM, Dynamical Systems based Soil Mechanics)은 흙의 변형을 동역학계의 거동으로 설명하는 토질역학적 접근 방식이다. DSSM은 흙 변형이 입자가 무작위 전단변형률에서 최종 위치로 이동하는 푸아송 과정임을 가정한다.^[31]

DSSM은 모래를 포함한 흙이 일정한 변형률 조건에서 전단될 때, 전단응력, 유효 압축응력, 간극비의 변화가 없는 정상 상태에 도달한다는 사실에 기반한다. 정상 상태는 [http://www.soilmechanics.us/dssm/uncategorized/appendix-4-dr-steve-poulos-interview/ 스티브 J. 풀로스]가 아서 카사그란데의 가설을 바탕으로 정의했다.^[27] 정상 상태는 통계적으로 일정한 구조를 지정한다는 점에서 임계 상태와는 다르며, 정상 상태 값은 변형률에 약간 의존한다.

DSSM은 자연계의 많은 시스템이 정상 상태에 도달하는 것처럼, 흙 전단 역시 동역학계로 설명될 수 있다는 점을 보여준다.^[28]^[29] 흙 전단 동역학계의 물리적 기반은 입자가 무작위 전단 변형률에서 정상 상태로 이동하는 푸아송 과정이다.^[30]

DSSM은 모래를 포함한 응력-변형 곡선, 민감 점토와 실트의 파괴 후 영역을 잘 설명할 수 있다. 또한 다음과 같이 기존 토질역학의 핵심 관계들을 설명한다.^[32]

정규화된 배수되지 않은 최대 전단강도가 과압밀비의 로그 값에 따라 변하는 이유
응력-변형 곡선이 초기 유효 압축 응력으로 정규화되는 이유
1차원 압밀에서 간극비가 유효 수직 응력의 로그 값에 따라 변해야 하는 이유
1차 압밀 종료 곡선이 정적 하중 증분에 대해 고유한 이유
크리프 값 Cα와 압축 지수 Cc의 비율이 광범위한 토양에 대해 거의 일정해야 하는 이유

참조

_[1] 서적 Fundamentals of soil behavior, Third edition John Wiley and Sons, Inc.
_[2] 서적 Soils and Waves: Particulate Materials Behavior, Characterization and Process Monitoring Wiley
_[3] 서적 Soil Mechanics – 2nd ed Spon Press
_[4] 서적 A Guide to Soil Mechanics Macmillan Press
_[5] 웹사이트 Built Environment – Routledge http://www.tandfbuil[...] 2017-01-14
_[6] 서적 Soil Mechanics Wiley
_[7] 학술지 Theory of Effective Stress in Soil and Rock and Implications for Fracturing Processes: A Review
_[8] 웹사이트 ASTM Standard Test Methods of Particle-Size Distribution (Gradation) of Soils using Sieve Analysis http://www.astm.org/[...] 2011-08-10
_[9] 학술지 Classification of Soils for Engineering Purposes: Annual Book of ASTM Standards http://www.astm.org/[...] American Society for Testing and Materials 2010-08-31
_[10] 서적 Soil Behavior and Critical State Soil Mechanics Cambridge University Press
_[11] 서적 Disturbed soil properties and geotechnical design Thomas Telford
_[12] 웹사이트 ASTM Standard Test Methods for Minimum Index Density and Unit Weight of Soils and Calculation of Relative Density http://www.astm.org/[...] 2011-09-07
_[13] 서적 Smith's Elements of Soil Mechanics John Wiley and Sons, Inc.
_[14] 서적 The handbook of groundwater engineering Taylor & Francis
_[15] 서적 Seepage, Drainage, and Flow Nets Wiley
_[16] 학술지 Soil piping and stream channel initiation
_[17] 웹사이트 Sandboils 101: Corps has experience dealing with common flood danger http://www.hq.usace.[...] US Army Corps of Engineers 2006-08-29
_[18] 서적 Soil Mechanics in Engineering Practice https://books.google[...] John Wiley & Sons, Inc.
_[19] 학술지 Fractal structure of pores in clay soil
_[20] 서적 An Introduction to Geotechnical Engineering Prentice-Hall, Inc.
_[21] 서적 Theoretical Soil Mechanics John Wiley and Sons
_[22] 서적 Soil mechanics in Engineering Practice, Third Edition John Wiley & Sons, Inc.
_[23] 서적 Advance Dam Engineering for Design, Construction, and Rehabilitation: Liquefaction Related Phenomena Van Nostrand Reinhold
_[24] 웹사이트 Slope Stability http://www.publicati[...] United States Army Corps of Engineers 2003-10-03
_[25] 웹사이트 Slope Stability Calculator http://www.wise-uran[...] 2006-12-14
_[26] 학술지 A method for locating critical slip surfaces in slope stability analysis: Discussion https://zenodo.org/r[...]
_[27] 학술지 The Steady State of Deformation
_[28] 학술지 Constitutive Model of Soil Based on a Dynamical Systems Approach
_[29] 학술지 A Dynamical Systems Based Approach to Soil Shear
_[30] 학술지 Physical Basis and Validation of a Constitutive Model for Soil Shear Derived from Micro-Structural Changes
_[31] 학술지 Generalised dynamical systems soil deformation model
_[32] 서적 Dynamical Systems-Based Soil Mechanics https://www.crcpress[...] CRC Press/Balkema 2017-05-14
_[33] 웹사이트 日本工業標準調査会標準部会土木技術専門委員会（第19回）－議事録 2007年12月5日 http://www.meti.go.j[...] 経済産業省
_[34] 서적 토목기사 과년도 - 토질 및 기초 성안당
_[35] 서적 토목기사 과년도 - 토질 및 기초 성안당

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com