헥스
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
헥스는 육각형 보드에서 두 명의 참가자가 서로의 변을 연결하는 것을 목표로 하는 전략 게임이다. 1942년 덴마크의 수학자 피트 하인에 의해 고안되었으며, 존 내시도 독립적으로 유사한 게임을 개발했다. 각 플레이어는 번갈아 가며 자신의 색깔 돌을 보드에 놓고, 자신의 돌로 마주보는 두 변을 연결하면 승리한다. 선공의 유리함을 보완하기 위해 스왑 규칙이 적용된다. 헥스는 무승부가 불가능하며, 섀넌의 헥스 머신, 컴퓨터 알고리즘 개발 등 다양한 연구가 진행되었다. 헥스는 PSPACE-완전 문제로, 렉스, Y 게임 등 변형 게임도 존재하며, 컴퓨터 올림피아드 정식 종목으로 채택될 정도로 널리 알려져 있다.
더 읽어볼만한 페이지
- PSPACE-완전 문제 - 오델로
오델로는 8x8 판에서 흑돌과 백돌을 사용하여 상대방의 돌을 가두어 뒤집는 보드 게임으로, 간단한 규칙 속에 깊이 있는 전략과 심리전을 요구하며 "배우기는 1분, 마스터하기는 평생"이라는 캐치프레이즈로 알려져 있다. - PSPACE-완전 문제 - 창고지기
창고지기는 1981년 이마바야시 히로유키가 개발한 퍼즐 게임으로, 플레이어가 상자를 밀어 정해진 위치에 놓는 방식으로 진행하며, 단순한 규칙과 달리 높은 난이도를 가진다. - 종이-연필 게임 - 틱택토
틱택토는 두 경기자가 3×3 칸에 O나 X를 번갈아 써서 가로, 세로, 대각선으로 같은 표를 만들면 이기는 놀이로, 최적 전략 시 무승부가 잦아 아이들이 즐기며 인공지능 교육 도구로도 쓰인다. - 종이-연필 게임 - 커넥트포
커넥트 포는 두 명의 플레이어가 7열 6행 격자판에 자신의 디스크를 떨어뜨려 가로, 세로, 대각선으로 4개를 먼저 연결하는 완전 정보 2인용 제로섬 게임이다. - 보드 게임 - 마작
마작은 4명이 144개의 패, 칩, 주사위 등을 사용하여 4개의 조와 1개의 머리로 14개의 패를 완성하는 것을 목표로 하는 게임이며, 19세기 중국에서 시작되어 현재 다양한 국가에서 즐기는 보드 게임이다. - 보드 게임 - 카르카손 (보드 게임)
카르카손은 타일을 놓아 중세 시대 풍경을 만들고 미플을 배치하여 소유권을 주장하며 점수를 얻는 보드 게임으로, 다양한 확장팩과 파생 작품, 비디오 게임으로 출시되었고 토너먼트와 세계 선수권 대회가 개최될 정도로 인기가 많다.
| 헥스 | |
|---|---|
| 게임 개요 | |
| 종류 | 보드 게임, 추상 전략 게임, 연결 게임 |
| 플레이어 수 | 2 |
| 준비 시간 | 없음 |
| 플레이 시간 | 30분 – 2시간 (11×11 보드 기준) |
| 무작위성 | 없음 |
| 필요 기술 | 전략, 전술 |
| 역사 | |
| 개발 시기 | 1942년–현재 |
| 개발자 | |
| 발명가 | 피에트 헤인, 존 포브스 내시 |
| 기타 | |
| 퍼블리셔 | 파커 브라더스(Parker Brothers) |
2. 규칙
헥스는 보통 11×11 크기의 육각형 격자 보드에서 진행되지만, 다른 크기도 가능하다. 각 플레이어는 빨간색과 파란색(또는 검은색과 흰색) 중 하나의 색깔을 선택하고, 보드에서 서로 마주 보는 두 변을 각자에게 할당받는다.
1942년 덴마크의 수학자 피에트 헤인이 '폴리곤'이라는 이름으로 게임을 발명하여 닐스 보어 연구소에서 처음 소개했다. 헤인은 게임 이름을 Con-tac-tix로 변경했지만,[2][3] 1942년 12월 26일 덴마크 신문 ''폴리티켄''에 기고한 글에서 'Polygon'이라는 이름을 사용했기 때문에 덴마크에서는 이 이름으로 알려졌다.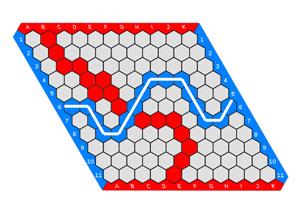
선공이 유리하기 때문에, 이 게임에서는 스왑 규칙(파이 규칙)이 적용된다. 첫 번째 플레이어가 첫 번째 수를 둔 후, 두 번째 플레이어가 선공과 후공을 바꿀지 선택할 수 있다. 
3. 역사
1948년 또는 1949년에 존 포브스 내시가 프린스턴 대학교에서 이 게임을 재발견했다.[4][5] 마틴 가드너에 따르면, 내시의 동료들은 이 게임을 내시 또는 존이라고 불렀는데, 후자의 이름은 육각형 욕실 타일에서 플레이할 수 있다는 사실에서 기인했다.[4]
1952년, 파커 브라더스는 "헥스(Hex)"라는 이름으로 게임 버전을 출시했고, 이 이름이 굳어졌다.[4]
1950년경, 클로드 섀넌과 E. F. 무어는 저항 네트워크를 기반으로 하는 아날로그 헥스 게임 기계를 제작했다.[8] 이 기계는 상당히 훌륭한 헥스 게임을 했다.
하인은 1942년 헥스가 무승부로 끝날 수 없다는 것과 선공이 이론적으로 승리 전략을 가지고 있다는 것을 알았다.[1] 1952년 존 내시는 대칭적인 보드에서 선공에게 승리 전략이 있음을 증명했다.[1] 이후 헥스는 PSPACE-완전임이 증명되었다.[11] 2002년에는 7x7 보드에서의 승리 전략이 발견되었고, 2000년대에는 무차별 대입 탐색 알고리즘으로 9x9 보드까지 완전히 해결되었다. 2019년에는 인공지능 프로그램 Mootwo가 인간 최고수를 상대로 승리했다.
3. 1. 발명
1942년 덴마크의 수학자 피에트 헤인이 '폴리곤(Polygon)'이라는 이름으로 처음 고안하여 닐스 보어 연구소에서 소개했다.[2][3][50] 헤인은 이 게임을 'Con-tac-tix'라고도 불렀지만, 덴마크에서는 "폴리곤"이라는 이름으로 알려졌다.[50] 헤인은 덴마크 신문 ''폴리티켄''에 이 게임을 소개하는 기사를 기고했으며, 관련 소책자는 5만 부가 발행되었다.[51]
3. 2. 존 내시의 재발견
1948년 또는 1949년에 프린스턴 대학교의 존 포브스 내시가 이 게임을 독자적으로 재발견했다.[4][5] 내시의 동료들은 이 게임을 '내시(Nash)' 또는 '존(John)'이라고 불렀는데, '존'이라는 이름은 육각형 욕실 타일에서 플레이할 수 있다는 사실에서 유래했다.[4]
마틴 가드너는 피트 하인이 먼저 이 게임을 발명했다는 사실은 논쟁의 여지가 없다고 판단했고, 내시에게 의심의 여지를 주는 것이 관대하다고 판단하여 내시가 독자적으로 재발견 한것으로 결론 내렸다.[1][6]
3. 3. 출판 및 상용화
1942년, 헤인은 '폴리곤'이라는 이름으로 50매짜리 게임 패드를 배포했다.[1] 1952년, 파커 브라더스(Parker Brothers)는 '헥스(Hex)'라는 이름으로 게임 버전을 출시했고, 이 이름이 굳어졌다.[4] 1968년에는 'Con-tac-tix'라는 이름으로도 버전을 판매했다.[2] 1974년 3M 종이 게임 시리즈의 게임 중 하나로도 출시되었으며, 5x 크기의 50매짜리 헥스 격자 패드가 들어 있었다. 현재 Nestorgames에서 11×11 크기, 14×14 크기 및 19×19 크기의 헥스 보드를 출판하고 있다.[7]
3. 4. 섀넌의 헥스 머신
1950년경, 클로드 섀넌과 E. F. 무어는 모서리(edge)에 저항을, 꼭짓점(vertex)에 전구를 사용한 저항 네트워크를 기반으로 하는 아날로그 헥스(Hex) 게임 기계를 제작했다.[8] 둬야 할 수는 네트워크의 특정 안장점(saddle point)에 해당했다. 이 기계는 상당히 훌륭한 헥스 게임을 했다. 이후, 게임을 해결하고 헥스 게임을 하는 컴퓨터 알고리즘을 개발하려는 연구자들은 섀넌의 네트워크를 모방하여 강력한 컴퓨터 플레이어를 만들었다.[9]
3. 5. 연구 연표
1942년, 피에트 하인은 헥스가 무승부로 끝날 수 없음을 확인했으며, 선공이 이론적으로 승리 전략을 가지고 있다는 것을 알았다.[1]
1952년, 존 내시는 대칭적인 보드에서 선공이 승리 전략을 가지고 있음을 증명하는 존재 증명을 작성했다.[1]
1964년, 알프레드 레만은 헥스가 이진 매트로이드로 표현될 수 없어, 섀넌 스위칭 게임과 같은 결정적인 승리 전략을 사용할 수 없음을 보였다.[10]
1981년, 슈테판 라이시는 헥스가 PSPACE-완전임을 증명했다.[11]
2002년, 7×7 보드에서 첫 번째 명시적 승리 전략 (축소 유형 전략)이 설명되었다.
2000년대에 무차별 대입 탐색 컴퓨터 알고리즘을 사용하여, 9×9 크기까지의 헥스 보드가 완전히 해결되었다 (2016년 기준).
2019년 10월 30일, 프로그램 Mootwo는 LittleGolem에서 최고의 Elo 순위를 가진 인간 플레이어를 상대로 승리했다.
4. 이론 및 전략
헥스 게임에서는 두 번째 참가자가 반드시 이기는 '승리 전략'이 있다고 가정할 때, 첫 번째 참가자는 임의의 육각형에 칩을 놓고 자신이 두 번째 참가자인 것처럼 게임을 진행하면 된다. 만약 처음에 놓은 칩이 필요한 경우, 다른 곳에 칩을 놓고 전략을 계속하면 첫 번째 참가자가 승리하게 된다. 이는 두 번째 참가자의 '승리 전략' 존재에 모순되므로, 먼저 하는 사람이 유리하다.[67]
헥스 게임은 무승부가 불가능하다. 한 참가자가 왼쪽과 오른쪽 변을 파란색으로 연결해야 한다고 할 때, 연결된 모든 파란색 육각형 집합을 'B'라고 하자. 'B'가 양쪽 변을 이으면 파란색 참가자가 승리하고, 그렇지 않으면 'B' 오른쪽 육각형들이 빨간색이 되어 위쪽과 아래쪽 변을 연결하여 빨간색 참가자가 승리한다.[68]
4. 1. 이론
헥스 게임은 무승부가 나올 수 없다는 것이 증명되었는데, 이를 "헥스 정리"라고 부른다. 보드에 돌이 어떻게 채워지든, 항상 자신의 가장자리를 연결한 플레이어가 단 한 명만 존재한다.[1] Piet Hein영어은 "상대방의 장벽은 당신의 연결이다"라고 표현했다.[1] 존 R. 피어스의 저서에 엄밀한 증명이 처음 게재되었다.[63] 데이비드 게일은 헥스의 결정성이 2차원 브라우어 고정점 정리와 동치임을 보였다.[26]헥스의 무승부 불가능성을 간단히 증명하면 다음과 같다. 빨간색 가장자리 중 하나의 연결된 구성 요소를 생각한다. 이 구성 요소는 반대쪽 빨간색 가장자리를 포함하거나, 그렇지 않은 경우 파란색 돌이 연결된 구성 요소의 경계를 따라 파란색의 승리 경로를 형성한다. 육각형 격자에서는 두 셀이 가장자리에서만 만나거나 전혀 만나지 않을 수 있기 때문에 연결된 구성 요소의 개념이 명확하게 정의된다.
''n''×''n'' 크기의 헥스 게임에서, 선공은 이론적으로 승리 전략을 가진다. (전략 훔치기 논법)[4] 이는 존 내시가 증명하였다.[1] 증명 과정은 다음과 같다.
# 헥스는 완전 정보를 가진 유한한 2인 게임이므로, 체르멜로의 정리에 따라 선공 또는 후공이 승리 전략을 가지거나, 둘 다 무승부를 강제할 수 있다.
# 무승부는 불가능하므로, 선공 또는 후공이 승리 전략을 가진다.
# 후공이 승리 전략을 가지고 있다고 가정하자.
# 이제 선공은 임의의 수를 둔다. 그 후, 위에서 가정한 승리하는 후공 전략을 사용한다. 이 전략을 사용하는 과정에서 임의의 수가 놓인 칸에 수를 두어야 하는 경우, 다른 임의의 수를 둔다.[27] 이러한 방식으로 항상 보드에 조각 하나가 더 있는 상태로 승리 전략을 사용한다.
# 이 추가 조각은 선공이 승리 전략을 모방하는 데 방해가 될 수 없다. 왜냐하면 추가 조각은 결코 불리하게 작용하지 않기 때문이다. 따라서 선공이 이길 수 있다.
# 후공에게 승리 전략이 있다는 가정이 모순되었으므로, 후공에게는 승리 전략이 없다.
# 결과적으로, 선공에게 승리 전략이 있어야 한다.
계산 복잡도 이론에서 헥스는 "PSPACE-완전"으로 여겨진다.[11] 이는 바둑이나 체커(이들은 "EXPTIME-완전"으로 여겨진다)보다 해석에 소요되는 계산량이 적다는 것을 의미한다.
11×11 헥스에서, 상태 공간 복잡성은 대략 2.4×1056이고;[31] 체스는 4.6×1046이다.[32] 게임 트리 복잡성은 대략 1098이며[33] 체스는 10123이다.[34]
2002년, 7×7 크기의 헥스 보드에서 선공하는 플레이어의 명시적인 승리 전략이 발견되었다.[35] 2009년에는 8x8, 2013년에는 9x9 보드의 모든 오프닝에 대한 해법이 발견되었다.[38]
4. 2. 전략
헥스에서 이기기 위해서는 "안전하게 연결된" 패턴을 만들고, 이를 "경로"로 연결하는 것이 핵심이다. "브릿지"는 안전하게 연결된 패턴의 간단한 예시이다."안전하게 연결된" 패턴은 상대방이 어떻게 플레이하든, 플레이어의 색상의 돌과 엣지 방향으로 인접한 돌의 끊어지지 않는 시퀀스인 체인으로 연결될 수 있는 열린 공간으로 구성된다.[18] 이러한 패턴 중 가장 간단한 것 중 하나는 다이아몬드 모양의 같은 색상의 돌 2개와 비어 있는 공간 2개로 구성된 브릿지인데, 두 돌은 서로 닿지 않는다.[19] 상대방이 두 공간 중 하나에 플레이하면, 플레이어는 다른 공간에 플레이하여 연속적인 체인을 만든다. 돌을 엣지에 연결하는 안전하게 연결된 패턴도 있다.[20]
이러한 간단한 패턴 외에도 복잡한 패턴들이 존재하며, 이러한 패턴들을 합성하고 연결 강도를 평가하는 능력이 헥스 게임에서 승리하기 위한 중요한 전략이 된다.[17]
5. 변형 게임
미제르는 "렉스(Rex)"라고 불리며, 각 플레이어는 상대방이 체인을 만들도록 강요하려고 시도한다. 렉스는 헥스보다 느린데, 동일한 크기의 비어있는 보드에서는 패배하는 플레이어가 보드가 완전히 채워질 때까지 패배를 늦출 수 있기 때문이다.[40] 크기가 다른 보드에서는 더 멀리 떨어져 있는 측면을 가진 플레이어가 먼저 시작하는 사람에 관계없이 이길 수 있다.[41] 크기가 같은 보드에서는 한 변당 셀 수가 짝수일 경우 선공 플레이어가 이길 수 있고, 홀수일 경우 후공 플레이어가 이길 수 있다.[42][43] 짝수 보드에서는 선공 플레이어의 승리 수 중 하나가 항상 예각 모서리에 돌을 놓는 것이다.[40]
Y 게임은 육각형의 삼각 격자에서 플레이하는 헥스 게임이다. 목표는 두 플레이어 중 한 명이 삼각형의 세 변을 모두 연결하는 것이다. Y는 헥스 보드의 모든 위치를 더 큰 Y 보드의 동등한 위치로 나타낼 수 있다는 점에서 헥스의 일반화이다.
하바나는 헥스를 기반으로 하는 보드 게임으로,[44] 육각형 타일로 구성된 보드 공간을 가지고 있지만, 보드 자체가 큰 육각형 모양이며, 세 가지 패턴 중 하나를 형성하면 승리한다.
Projex는 실사영사 평면에서 플레이하는 헥스의 변형으로, 플레이어는 비가역적 루프를 만드는 것을 목표로 한다.[45] 헥스와 마찬가지로 무승부는 없으며, 두 플레이어 모두 이기는 연결을 가질 수 있는 위치는 없다.
다크 헥스(Dark Hex, 일명 팬텀 헥스(Phantom Hex))는 헥스의 불완전 정보 버전이다.[46] 게임 중 플레이어는 먼저 발견하지 않는 한 서로의 돌을 볼 수 없다. 게임은 심판의 입회하에 진행되며, 각 플레이어는 먼저 자신의 수가 충돌인지 여부를 확인한다. 이 점을 기반으로 게임은 다양한 버전으로 진행된다.
헥스는 텔레비전 게임 쇼 ''블록버스터''의 질문판으로 구현되기도 했다. "이동"을 하려면, 참가자는 질문에 정확히 답해야 했다. 이 보드는 4개의 육각형이 5개의 교대로 배열된 열로 이루어져 있었으며, 솔로 플레이어는 4번의 이동으로 위에서 아래로 연결할 수 있었고, 2인 팀은 5번의 이동으로 왼쪽에서 오른쪽으로 연결할 수 있었다.
헥스는 반대로 대변을 먼저 연결한 쪽이 지는 게임이다.
6. 대회
2016년을 기준으로 브라질, 체코, 덴마크, 프랑스, 독일, 이탈리아, 네덜란드, 노르웨이, 폴란드, 포르투갈, 스페인, 영국 및 미국에서 오프라인 헥스 대회가 개최되고 있다. 프랑스 파리의 국제 수학 게임 위원회에서는 2013년부터 매년 헥스 대회를 개최하고 있다.[47] 헥스는 컴퓨터 올림피아드의 정식 종목이며, 이 대회에서는 파이 규칙이 사용된다.[47]
참조
[1]
서적
Hex, Inside and Out: The Full Story
CRC Press
[2]
서적
Con-tac-tix manual
https://www.hasbro.c[...]
Parker Brothers
[3]
서적
Hex, inside and out : the full story
CRC Press
[4]
서적
The Scientific American Book of Mathematical Puzzles & Diversions
https://archive.org/[...]
Simon and Schuster
[5]
뉴스
The Lost Years of a Nobel Laureate
https://www.nytimes.[...]
2017-08-23
[6]
서적
Hex, inside and out : the full story
CRC Press
[7]
웹사이트
nestorgames - fun to take away
https://www.nestorga[...]
2020-09-03
[8]
간행물
Computers and Automata
[9]
문서
A Hierarchical Approach to Computer Hex
[10]
간행물
A Solution of the Shannon Switching Game
Society for Industrial and Applied Mathematics
[11]
간행물
Hex ist PSPACE-vollständig
[12]
간행물
Hexmaster
https://archive.org/[...]
2019-01-18
[13]
Citation
facebookincubator/Polygames
https://github.com/f[...]
Facebook Incubator
2020-05-29
[14]
웹사이트
Open-sourcing Polygames, a new framework for training AI bots through self-play
https://ai.facebook.[...]
2020-05-29
[15]
Arxiv
Polygames: Improved Zero Learning
2020-01-27
[16]
Arxiv
Innateness, AlphaZero, and Artificial Intelligence
2018-01-17
[17]
문서
Browne p.
[18]
문서
Browne, p.28
[19]
문서
Browne, pp. 29–30
[20]
문서
Browne, pp. 71–77
[21]
문서
Browne, p.
[22]
문서
Lasker, p.
[23]
간행물
Hex and combinatorics
2006-10-06
[24]
문서
Rand Corp. technical report D-1164: Some Games and Machines for Playing Them
https://web.archive.[...]
2017-01-21
[25]
서적
Hex, inside and out : the full story
CRC Press
[26]
간행물
The Game of Hex and Brouwer Fixed-Point Theorem
Mathematical Association of America
[27]
문서
If the board has been completely filled, then one player must have won already, and it must be the first player since they have been playing a winning strategy.
[28]
간행물
A Combinatorial Problem Which is Complete in Polynomial Space
[29]
간행물
Hex ist PSPACE-vollständig (Hex is PSPACE-complete)
[30]
문서
Computational Complexity: A Modern Approach
Cambridge University Press
[31]
서적
Hex Strategy
A.K. Peters, Ltd.
2000
[32]
웹사이트
Number of chess diagrams and positions
http://homepages.cwi[...]
[33]
문서
Games solved: Now and in the future
[34]
문서
Searching for Solutions in Games and Artificial Intelligence
[35]
웹사이트
On a decomposition method for finding winning strategy in Hex game
https://web.archive.[...]
2012-04-02
[36]
간행물
Unpublished white papers
www.ee.umanitoba.com[...]
[37]
웹사이트
Solving 8x8 Hex
http://webdocs.cs.ua[...]
2011-07-16
[38]
논문
Scalable Parallel DFPN Search
http://webdocs.cs.ua[...]
2013
[39]
간행물
Scientific American
1957-07
[40]
서적
Hex, inside and out : the full story
CRC Press
[41]
서적
Hex, inside and out : the full story
CRC Press
[42]
문서
[43]
문서
[44]
웹사이트
How I invented games and why not
https://www.mindspor[...]
2020-10-19
[45]
웹사이트
Projex
https://boardgamegee[...]
2018-02-28
[46]
웹사이트
Dark Hex: A Large Scale Imperfect Information Game
https://scholar.goog[...]
[47]
웹사이트
ICGA – Computer Olympiad
https://icga.org/?pa[...]
[48]
웹사이트
Games and Puzzles 1973-08: Iss 16
https://archive.org/[...]
A H C Publications
1973-08
[49]
웹사이트
Jeux & stratégie 06
https://archive.org/[...]
1980-12
[50]
서적
Hex, inside and out: the full story
CRC Press Taylor & Francis Group
2019
[51]
서적
Hex, inside and out: the full story
CRC Press, Taylor and Francis Group
2019
[52]
서적
Hex, inside and out: the full story
CRC Press Taylor & Francis Group
2019
[53]
서적
ガードナーの数学パズル・ゲーム (完全版 マーティン・ガードナー数学ゲーム全集1)
日本評論社
2015-04-25
[54]
서적
ビューティフル・マインド 天才数学者の絶望と奇跡
新潮社
2002-03-15
[55]
서적
Hex, inside and out: the full story
CRC Press, Taylor and Francis Group
2019
[56]
서적
Hex, inside and out: the full story
CRC Press, Taylor and Francis Group
2019
[57]
논문
MATHEMATICAL GAMES
[58]
논문
Hex and combinatorics
https://linkinghub.e[...]
2006-10-06
[59]
서적
Hexaflexagons and other mathematical diversions: the first Scientific American book of puzzles & games
University of Chicago Press
1988
[60]
서적
マーティン・ガードナー:ガードナーの数学パズル・ゲー
日本評論社
[61]
서적
Hex, inside and out: the full story
CRC Press Taylor & Francis Group
2019
[62]
논문
Topological games at Princeton, a mathematical memoir
https://linkinghub.e[...]
2009-07-01
[63]
서적
Symbols, Signals, and Noise: The Nature and Process of Communication
Harper Modern Science Series, Harper
[64]
논문
The Game of Hex and the Brouwer Fixed-Point Theorem
https://www.tandfonl[...]
1979-12
[65]
서적
Hexaflexagons and other Mathematical Diversions - The First Scientific American Book of Puzzles and Games
Simon and Schuster
[66]
웹사이트
Game of Hex
http://mathworld.wol[...]
[67]
웹인용
Hex
http://maarup.net/th[...]
2012-05-03
[68]
간행물
Math. Magazine
1976-03
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com