0의 0제곱
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
0의 0제곱은 수학에서 0을 0제곱하는 경우에 대한 논의를 다룬다. 이 값은 이산 지수, 다항식과 멱급수, 연속 지수, 복소 지수 등 다양한 맥락에서 정의가 다르다. 00을 1로 정의하는 것이 여러 공식의 간결성을 위해 편리하며, 컴퓨터 과학자 도널드 커누스는 이를 강력하게 지지한다. 집합론적 관점에서는 공집합에서 공집합으로의 사상이 유일하게 존재하므로 1로 정의된다. 그러나 연속 지수와 복소 지수에서는 0⁰이 부정형이거나 정의되지 않는다. 컴퓨터에서는 IEEE 754-2008 부동 소수점 표준에 따라 1로 처리되며, 대부분의 프로그래밍 언어에서도 1로 계산된다.
더 읽어볼만한 페이지
- 0 - 3월 0일
- 0 - 영벡터
- 거듭제곱 - 지수 함수
지수 함수는 양의 상수 *a*를 밑으로 하는 *y = ax* 형태의 함수이며, 특히 자연로그의 역함수인 *ex*는 다양한 정의와 응용을 가지며 복소수로 확장될 수 있다. - 거듭제곱 - 반감기
반감기는 어떤 양이 원래 값의 절반으로 줄어드는 데 걸리는 시간을 의미하며, 방사성 붕괴, 화학 반응 등 다양한 분야에서 활용되고 방사성 동위원소의 안정성을 나타내는 지표이다. - 컴퓨터 산술 - IEEE 754
IEEE 754는 부동소수점 숫자를 표현하고 처리하기 위한 국제 표준으로, 다양한 형식과 연산, 반올림 규칙, 예외 처리 등을 정의한다. - 컴퓨터 산술 - 1의 보수
1의 보수는 이진수에서 양수는 일반적인 이진수로, 음수는 양수의 각 비트를 반전시켜 표현하며, 덧셈 시 자리올림수가 발생하면 결과값에 더해야 하고, 0을 중복 표현하는 단점으로 현대에는 2의 보수가 주로 사용된다.
| 0의 0제곱 | |
|---|---|
| 정의 | |
| 값 | 00 = 1 |
| 논쟁 상태 | 논쟁 중 |
| 수학적 속성 | |
| 불확정 형식 | 00은 극한에서 불확정 형식임. |
| 조합론적 해석 | 빈 튜플은 정확히 하나 존재함. 따라서 00 = 1로 정의하는 것이 자연스러움. |
| 이항 정리 | 이항 정리를 확장하기 위해 00 = 1로 정의해야 함. |
| 거듭제곱 급수 | 거듭제곱 급수를 표현하기 위해 00 = 1로 정의해야 함. |
| 연속성 | xy는 (0, 0)에서 연속이 아님. |
| 미분 가능성 | xy는 (0, 0)에서 미분 불가능함. |
| 프로그래밍 언어 | |
| 프로그래밍 언어 | 대부분의 프로그래밍 언어에서 00은 1로 계산됨. |
| 예외 | 일부 소프트웨어(예: 엑셀)에서는 00을 오류로 처리함. |
2. 이산 지수
자연수 지수를 포함하는 많은 공식에서 $0^0$을 1로 정의하는 것이 편리하다. 예를 들어, $b^0$의 해석에는 다음과 같은 것들이 있으며, 이들은 모두 $0^0 = 1$을 이끌어낸다.
- $b^0$을 빈 곱으로 해석하면 값은 1이다.
- $b^0$의 조합적 해석은 $b$개의 원소를 가진 집합에서 원소의 0-튜플의 개수를 의미하며, 0-튜플은 정확히 하나이다.
- $b^0$의 집합론적 해석은 공집합에서 $b$개의 원소를 가진 집합으로의 함수의 개수를 의미하며, 이러한 함수는 정확히 하나 (공함수)이다.
다항식을 평가할 때도 $0^0$을 1로 정의하는 것이 편리하다. 다항식은 항별로 더해지고, 분배 법칙과 지수에 대한 일반적인 규칙을 적용하여 곱해진다. 또한, 다항식은 $x$를 실수로 특수화하여 평가할 수 있는데, 0을 포함한 각 실수 $r$에 대해 $r^0 = 1$이다.
$0^0 = 1$로 정의해야 할 필요가 있는 다항식 항등식은 많다. 예를 들어 이항 정리 $(1+x)^{n}=\sum_{k=0}^{n}\binom{n}{k}x^{k}$은 $x=0$일 때 $0^0 = 1$인 경우에만 성립한다.
마찬가지로, 멱급수의 환은 $x$의 모든 특수화를 위해 $x^0$을 1로 정의해야 한다. 예를 들어, $\frac{1}{1-x}=\sum_{n=0}^{\infty}x^n$ 및 $e^x=\sum_{n=0}^{\infty}\frac{x^n}{n!}$과 같은 항등식은 $x=0$일 때 $0^0 = 1$인 경우에만 성립한다.
미적분학에서, 거듭제곱 법칙 $\frac{d}{dx}x^n=nx^{n-1}$은 $n=1$일 때 $x=0$에서 $0^0 = 1$인 경우에만 유효하다.
비음수 정수의 지수만을 다루는 경우, 다음 이유들로 $0$의 $0$제곱은 $1$로 정의되는 경우가 많다.
- 실수 $x$를 수직선상의 선형 변환으로 간주할 때, $x$의 $0$제곱은 항등 변환(실수 $1$에 대응)으로 간주한다.
- $x \neq 0$일 때 $x^0 = 1$이므로, 함수 $x^0$의 연속성을 위해 $x=0$일 때도 $0^0 = 1$로 정의한다.
- $0^0 = 1$로 정의하면, 여러 공식이나 증명에서 기술이 간단해진다.
컴퓨터 과학자 도널드 커누스는 $0^0$은 $1$이어야 한다고 주장한다. 그에 따르면, $x^0$는 여러 공식에 자주 나타나므로, $0^0 = 1$로 정의하는 것이 편리하다.
3. 다항식과 멱급수
다항식을 평가할 때, 00을 1로 정의하는 것이 편리하다. 다항식은 항별로 더해지고, 분배 법칙과 지수에 대한 일반적인 규칙을 적용하여 곱해진다. 다항식은 환을 형성하는데, 이 환의 곱셈 항등원은 다항식 x0이다. 즉, x0에 어떤 다항식 p(x)를 곱해도 p(x)이다. 또한, 다항식은 x를 실수로 특수화하여 평가할 수 있는데, 0을 포함한 각 실수 r에 대해 1 = r0 = 1이다. 같은 논리가 임의의 환으로 대체해도 적용된다.
많은 다항식 항등식을 위해 00 = 1로 정의하는 것이 필요하다. 예를 들어, 이항 정리 은 x = 0일 때 00 = 1인 경우에만 성립한다.
마찬가지로, 멱급수의 환은 x의 모든 특수화를 위해 x0을 1로 정의해야 한다. 예를 들어, 및 과 같은 항등식은 x = 0일 때 00 = 1인 경우에만 성립한다.
미적분학에서, 거듭제곱 법칙 은 n = 1일 때 x = 0에서 00 = 1인 경우에만 유효하다.
컴퓨터 과학자 도널드 커누스는 00은 1이어야 한다고 주장한다. 그에 따르면 0x라는 함수는 수학적 의의가 적은 반면, x0는 다양한 공식에 빈번하게 나타나므로, 이쪽을 기준으로 삼는 쪽이 형식적으로 편리하다. 예를 들어, 이항 정리 공식은 00 = 1로 했을 때만 x = 0에 대해 적용 가능해진다.
4. 연속 지수
대수 연산과 관련된 극한은 종종 부분식을 해당 극한으로 대체하여 평가할 수 있다. 결과 표현식이 원래 극한을 결정하지 못하면 해당 표현식은 부정형으로 알려져 있다. 0⁰은 이러한 부정형 중 하나이다.
와 가 모두 0으로 수렴하는 실수 값을 갖는 함수이고, 일 때, 의 극한은 함수 와 에 따라 0 이상의 실수, 가 되거나 발산할 수 있다. 예를 들어, 아래 각 극한은 형태를 가지며, ( (단측 극한))이지만, 그 값은 서로 다르다.
:
:
:
:
따라서, 두 변수 함수 는 }에서는 연속이지만, 0⁰을 어떻게 정의하든 }에서는 연속 함수로 확장될 수 없다.
하지만, 와 가 숫자 근처에서 해석 함수이고, 가 양수이면, 가 에 접근할 때 이다.
이는 함수의 극한을 통해 알 수 있다.[1][2]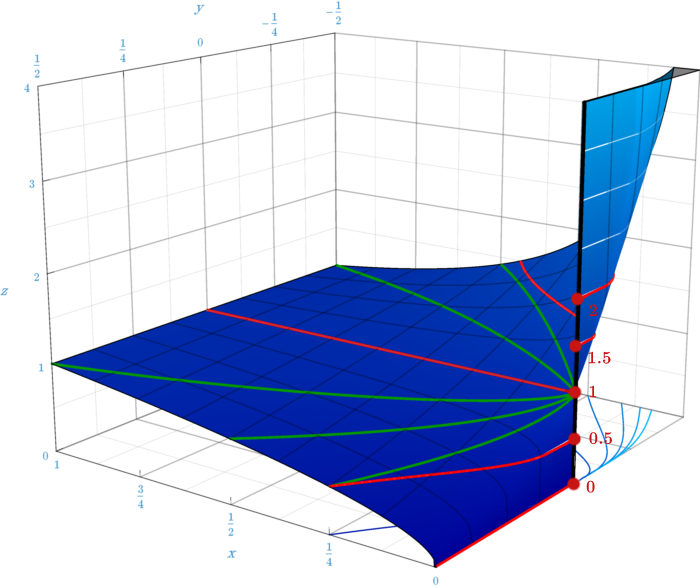
두 변수 함수 는 에서 연속이다. 그러나 (0, 0)을 포함한 에서는, 0⁰을 어떻게 정의하더라도 연속이 되지 않는다. 이는 원점에 접근하는 경로에 따라 극한값이 다르기 때문이다. 예를 들어:
- ''y'' 축 ()을 따라 접근하면:
:
- ''x'' 축 ()을 따라 접근하면:
:[10]
은 함수 와 의 극한이 모두 0일 때, 의 극한을 나타내기도 한다. 이 때 은 부정형이며, 극한값은 일정하지 않다.
극한이 1이 되는 충분 조건은 다음과 같다. 및 가 에서 실해석적이고, 양수 에 대해 에서 이면, 의 극한은 1이다.[11]
5. 복소 지수
복소수 영역에서 z≠0일 때 zw는 log z의 분기를 선택하고 z|z영어w를 e|e영어w log z|w log z영어로 정의하여 정의할 수 있다. z = 0에서 log z의 분기가 정의되지 않으므로, 0의 근방에서도 0w는 정의되지 않는다.
6. 역사
18세기 오일러는 0⁰ = 1임을 명시했다. 19세기 초 코시는 0⁰을 부정형 목록에 포함시켰다. 뫼비우스는 f(x)ᵍ(x) (f(x), g(x) → 0)의 극한이 항상 1이라고 잘못 주장했다.
현재 0⁰은 문맥에 따라 1로 정의되거나 정의되지 않은 것으로 간주된다. 크누스는 0⁰의 ''값''은 1과 같아야 하지만, ''극한 형식'' 0⁰은 부정형이라고 구별했다.
7. 컴퓨터에서의 처리
IEEE 754 부동 소수점 표준은 대부분의 부동 소수점 라이브러리 설계에 사용되며, 거듭제곱 계산을 위한 여러 연산을 권장한다. 표준에서는 0⁰을 다음과 같이 처리한다.
| 연산 | 처리 방식 |
|---|---|
| `pown` (지수가 정수인 경우) | 1 |
| `pow` | 1 |
| `powr` | NaN (Not-a-Number) |
`pow` 변형은 주로 C99의 `pow` 함수에서 영감을 받아 호환성을 위해 사용된다. `pown` 및 `powr` 변형은 거듭제곱 함수의 상충되는 사용법과 서로 다른 관점으로 인해 도입되었다.
C와 C++ 표준은 0⁰의 결과를 지정하지 않지만(도메인 오류가 발생할 수 있음), C의 경우 C99 이후부터 실수 부동 소수점 유형의 결과는 1로 요구된다. 자바 표준, .NET Framework 메서드 `System.Math.Pow`, 줄리아, 파이썬 또한 0⁰을 1로 취급한다. 루아의 `^` 연산자와 펄의 `` 연산자는 `00`의 결과가 플랫폼에 따라 다르다고 명시되어 있다.
R, SageMath, PARI/GP는 x⁰을 1로 계산한다. 매스매티카는 x⁰에 x에 대한 제약이 없더라도 1로 단순화하지만, 0⁰을 직접 입력하면 오류 또는 부정으로 처리한다. 매스매티카 및 PARI/GP는 정수 값과 부동 소수점 값을 구별하여, 지수가 정수 유형의 0이면 밑의 유형의 1을 반환하고, 값이 0인 부동 소수점 지수를 사용한 지수 연산은 정의되지 않거나, 부정 또는 오류로 처리한다.
8. 집합론적 관점
집합론에서 기수의 거듭제곱은 함수 집합의 크기로 정의된다. 공집합에서 공집합으로의 함수는 공집합 하나뿐이므로, 00 = 1로 정의된다.[8][9] 이는 서수의 거듭제곱에서도 마찬가지로 성립한다.
일반적으로 기수 κ영어, λ영어에 대해, 거듭제곱 λκ영어는 농도가 κ영어, λ영어인 임의의 집합을 각각 ''X'', ''Y''라 할 때, ''X''에서 ''Y''로의 사상의 개수(농도)로 정의된다.
:
여기서 ''Y''''X''는 ''X''에서 ''Y''로의 사상 전체의 집합이며, #는 집합의 농도를 나타낸다. (이 정의는 ''X''와 ''Y''의 선택에 의존하지 않는다.) 따라서 00는 ''X'' = ''Y'' = ∅ 의 경우에 해당하므로, 이다. 여기서 ∅에서 ∅로의 사상은 유일하게 존재하므로 (공사상), 이다. 따라서 00 = 1이다.
9. 반군론적 관점
반군에서 원소 의 거듭제곱 (은 양의 정수)은 개의 를 곱한 것으로 정의된다.[5] 모노이드(단위원을 갖는 반군)에서는 로 정의된다.[6] 특히 가 영원을 갖는 경우 이다.[7]
참조
[1]
논문
Indeterminate Forms of Exponential Type
https://www.jstor.or[...]
1978-06
[2]
논문
On Indeterminate Forms of Exponential Type
https://www.jstor.or[...]
2017-12
[3]
문서
Lp空間#p = 0 の場合
[4]
문서
math|''x'' {{=}} 0
[5]
문서
この定義は半群における積の[[結合法則|結合性]]より意味を持つ。
[6]
문서
さらに {{mvar|a}} が逆元を持つならば、それを {{math|''a''−1}} と表記し、負の整数 {{math|−''n''}} に対して {{math|1=''a''−''n'' = (''a''−1)''n''}} と表記する。
[7]
문서
整数の全体や実数の全体など、あるいは一般に単位元を持つ[[結合環]]は、乗法について零元を持つモノイドをなす。
[8]
서적
Theory of Sets
Springer
[9]
서적
Set Theory: A First Course
Cambridge University Press
[10]
문서
ここに、{{math|''x'' → +0}} は ''x'' が正の方向から 0 に近付くことを表す。なお、負の数 ''y'' に対して 0''y'' は定義されない。
[11]
웹사이트
sci.math FAQ: What is 0^0?
http://www.faqs.org/[...]
[12]
문서
"Since ln 0 does not exist, 0''z'' is undefined. For {{nowrap|Re ''z'' > 0}}, we define it arbitrarily as 0."(ln 0 は存在しないから、0''z'' は定義されていない。{{nowrap|Re ''z'' > 0}} に対しては、0 と定義する。){{harv|Carrier|Krook|Pearson|2005|p={{google books quote|id=M2IwKL-_HQ8C|page=15|15}}}}
[13]
문서
"For {{nowrap|1=''z'' = 0}}, {{nowrap|''w'' ≠ 0}}, we define {{nowrap|1=0''w'' = 0}}, while 00 is not defined."({{nowrap|1=''z'' = 0}}, {{nowrap|''w'' ≠ 0}} に対しては、{{nowrap|1=0''w'' = 0}} と定義するが、00 は定義しない。){{harv|Gonzalez|1991|p={{google books quote|id=ncxL7EFr7GsC|page=56|56}}}}.
[14]
웹사이트
0^0の計算結果
https://www.google.c[...]
Google전탁
[15]
문서
具体的には、Visual Basic Editor (VBE) のイミディエイトウィンドウ上で ?0^0 と打ち、Enter を押すと 1 と出てくる。
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com