맨위로가기

꼭짓점 (그래프 이론)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

그래프 이론에서 꼭짓점은 그래프를 구성하는 기본 요소로, 다른 꼭짓점과 연결될 수 있는 지점을 의미한다. 꼭짓점은 차수에 따라 고립 꼭짓점, 잎새 꼭짓점, 소스 꼭짓점, 싱크 꼭짓점 등으로 분류되며, 그래프 구조에 따라 절단 꼭짓점, 단순 꼭짓점, 유니버설 꼭짓점 등으로 분류된다. 또한, 독립 집합, 꼭짓점 덮개, 꼭짓점 공간 등과 같은 개념과 관련이 있으며, 레이블된 꼭짓점과 레이블되지 않은 꼭짓점으로 구분되기도 한다. 그래프의 꼭짓점은 다면체의 꼭짓점과 유사한 개념이지만, 추가적인 기하학적 구조를 갖는다는 차이가 있다.

더 읽어볼만한 페이지

  • 그래프 이론 - 다이어그램
    다이어그램은 2차원 기하학적 기호를 사용하여 정보를 시각적으로 표현하는 기술로, 과학, 공학, IT, 비즈니스 등 다양한 분야에서 활용되며 정보를 간략하게 나타내고 시각적 사고를 돕는다.
  • 그래프 이론 - 쾨니히스베르크의 다리 문제
    쾨니히스베르크의 다리 문제는 프레겔 강에 놓인 7개의 다리를 한 번씩만 건너 출발점으로 되돌아올 수 있는지 묻는 문제로, 오일러에 의해 그래프 이론적으로 분석되어 해결되었으며 그래프 이론의 탄생에 기여했다.
꼭짓점 (그래프 이론)
그래프 이론 기본 정보
정의그래프를 구성하는 기본 단위
다른 이름꼭짓점
마디
노드
연결모서리 (변)
차수해당 꼭짓점에 연결된 모서리의 수
인접두 꼭짓점이 모서리로 연결되어 있을 때, 서로 인접한다고 함
근방해당 꼭짓점에 인접한 모든 꼭짓점들의 집합
고립점다른 꼭짓점과 연결되지 않은 꼭짓점 (차수가 0)
잎 (종단점)차수가 1인 꼭짓점
그래프 차수열꼭짓점 차수를 내림차순으로 나열한 수열
관련 개념그래프 이론

2. 꼭짓점의 종류

그래프의 꼭짓점은 연결된 변의 수, 방향성, 그래프 내에서의 역할 등에 따라 여러 종류로 분류된다.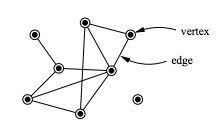

8개의 꼭짓점(그 중 하나는 고립)과 10개의 변을 가진 예시 네트워크.


그래프에서 꼭짓점에 인접한 변의 개수를 그 꼭짓점의 차수라 하며, 𝛿(v)로 표기한다.[1]

  • '''고립 꼭짓점''': 차수가 0인 꼭짓점이다.
  • '''잎새 꼭짓점''' ('''펜던트 꼭짓점'''): 차수가 1인 꼭짓점이다.


유향 그래프에서는 나가는 변의 개수인 밖차수(𝛿+(v)로 표기)와 들어오는 변의 개수인 안차수(𝛿−(v)로 표기)를 구별한다.[1]

  • '''소스 꼭짓점''': 안차수가 0인 꼭짓점이다.
  • '''싱크 꼭짓점''': 밖차수가 0인 꼭짓점이다.


절단 꼭짓점은 제거하면 나머지 그래프가 분리되는 꼭짓점이며, 꼭짓점 분리 집합은 제거하면 나머지 그래프를 작은 조각으로 분리하는 꼭짓점의 모음이다. k-정점 연결 그래프는 ''k''개 미만의 꼭짓점을 제거해도 항상 나머지 그래프가 연결된 상태로 유지되는 그래프이다. 독립 집합은 서로 인접하지 않은 꼭짓점들의 집합이고, 꼭짓점 덮개는 각 변의 적어도 하나의 끝점을 포함하는 꼭짓점의 집합이다.

단순 꼭짓점은 이웃들이 클리크를 형성하는 꼭짓점이다. 유니버설 꼭짓점은 그래프의 다른 모든 꼭짓점과 인접한 꼭짓점이다.

그래프는 어떤 꼭짓점을 다른 꼭짓점으로 매핑하는 대칭성을 가지면 정점-추이라고 한다. 그래프 열거와 그래프 동형의 맥락에서 '''레이블된 꼭짓점'''과 '''레이블되지 않은 꼭짓점'''을 구별하는 것이 중요하다. 레이블된 꼭짓점은 다른 레이블된 꼭짓점과 구별할 수 있도록 추가 정보가 연관된 꼭짓점이다. 두 그래프는 꼭짓점 간의 대응이 동일한 레이블을 가진 꼭짓점을 쌍으로 묶는 경우에만 동형으로 간주될 수 있다. 레이블되지 않은 꼭짓점은 그래프의 인접성만을 기반으로 다른 꼭짓점으로 대체될 수 있다.

그래프의 꼭짓점은 다면체의 꼭짓점과 유사하지만 동일하지는 않다.

2. 1. 차수에 따른 분류

그래프에서 꼭짓점의 차수(𝛿(v)로 표기)는 해당 꼭짓점에 연결된 변의 개수를 의미한다.[1] 차수에 따라 꼭짓점을 다음과 같이 분류할 수 있다.

  • 고립 꼭짓점: 차수가 0이다.
  • 잎새 꼭짓점 (펜던트 꼭짓점): 차수가 1이다.
  • 소스 꼭짓점: 유향 그래프에서 안차수가 0이다.
  • 싱크 꼭짓점: 유향 그래프에서 밖차수가 0이다.


단순 꼭짓점은 이웃들이 클리크를 형성하는 꼭짓점이다. 즉, 모든 두 이웃이 서로 인접해 있다. 유니버설 꼭짓점은 그래프의 다른 모든 꼭짓점과 인접한 꼭짓점이다.

2. 1. 1. 고립 꼭짓점

차수가 0인 꼭짓점으로, 어떤 변과도 연결되지 않은 꼭짓점이다.[1]

2. 1. 2. 잎새 꼭짓점 (펜던트 꼭짓점)

차수가 1인 꼭짓점을 잎새 꼭짓점(펜던트 꼭짓점)이라고 부르며, 하나의 변과만 연결된다.[1]

2. 1. 3. 유향 그래프에서의 꼭짓점

유향 그래프에서는 변의 방향에 따라 들어오는 변의 개수인 안차수(𝛿−(v)로 표기)와 나가는 변의 개수인 밖차수(𝛿+(v)로 표기)를 구분한다.[1] 소스 꼭짓점은 안차수가 0인 꼭짓점으로, 나가는 변만 있는 꼭짓점이다. 반대로 싱크 꼭짓점은 밖차수가 0인 꼭짓점으로, 들어오는 변만 있는 꼭짓점이다.[1]

2. 2. 그래프 구조에 따른 분류



그래프에서 꼭짓점에 인접한 변의 개수를 그 꼭짓점의 차수라 하며, 𝛿(v)로 표기한다. 차수에 따라 꼭짓점을 다음과 같이 분류할 수 있다.[1]

  • '''고립 꼭짓점''': 차수가 0인 꼭짓점으로, 어떤 변의 끝점도 아니다.
  • '''잎새 꼭짓점''' ('''펜던트 꼭짓점'''): 차수가 1인 꼭짓점이다.


유향 그래프에서는 들어오는 변의 개수인 안차수와 나가는 변의 개수인 밖차수를 구분한다.

  • '''소스 꼭짓점''': 안차수가 0인 꼭짓점이다.
  • '''싱크 꼭짓점''': 밖차수가 0인 꼭짓점이다.


유향 그래프에서, 어떤 정점 u의 forward star는 그 외향 변으로 정의된다. 정점 집합 V와 변 집합 E를 갖는 그래프 G에서, u의 forward star는

:\{(u, v) \in E\}\ [2]

로 표기된다.

2. 2. 1. 절단 꼭짓점

절단 꼭짓점은 해당 꼭짓점을 제거하면 나머지 그래프가 분리되는 꼭짓점이다. 즉, 절단 꼭짓점을 제거하면 그래프가 두 개 이상의 연결 요소로 분리된다.[1]

2. 2. 2. 꼭짓점 분리 집합

절단 꼭짓점은 제거하면 나머지 그래프가 분리되는 꼭짓점이다. 꼭짓점 분리 집합은 제거하면 나머지 그래프를 여러 개의 작은 조각으로 분리하는 꼭짓점들의 집합이다.[1]

2. 2. 3. k-정점 연결 그래프

k-정점 연결 그래프는 k개 미만의 꼭짓점을 제거해도 나머지 그래프가 연결된 상태로 유지되는 그래프이다.[1] 이러한 그래프에서 각 꼭짓점은 k-정점 연결성을 갖는다고 할 수 있다.

2. 2. 4. 단순 꼭짓점

어떤 꼭짓점의 이웃들이 클리크를 형성하는, 즉 모든 두 이웃 꼭짓점이 서로 인접해 있는 꼭짓점을 단순 꼭짓점이라고 한다.[1]

2. 2. 5. 유니버설 꼭짓점

유니버설 꼭짓점은 그래프의 다른 모든 꼭짓점과 인접한 꼭짓점이다.[1]

3. 꼭짓점과 관련된 개념



그래프에서 꼭짓점의 차수는 𝛿(v)로 표기하며, 꼭짓점에 인접한 변의 개수를 의미한다. '''고립 꼭짓점'''은 차수가 0인 꼭짓점, 즉 어떤 변의 끝점도 아닌 꼭짓점이다(예시 그림은 하나의 고립 꼭짓점을 보여준다).[1] '''잎새 꼭짓점''' ('''펜던트 꼭짓점'''이라고도 함)은 차수가 1인 꼭짓점이다. 유향 그래프에서는 𝛿+(v)로 표기하는 밖차수(나가는 변의 개수)와 𝛿−(v)로 표기하는 안차수(들어오는 변의 개수)를 구별할 수 있다. '''소스 꼭짓점'''은 안차수가 0인 꼭짓점이고, '''싱크 꼭짓점'''은 밖차수가 0인 꼭짓점이다. '''단순 꼭짓점'''은 이웃들이 클리크를 형성하는 꼭짓점이다: 모든 두 이웃은 인접해 있다. 유니버설 꼭짓점은 그래프의 다른 모든 꼭짓점과 인접한 꼭짓점이다.

절단 꼭짓점은 제거하면 나머지 그래프가 분리되는 꼭짓점이며, 꼭짓점 분리 집합은 제거하면 나머지 그래프를 작은 조각으로 분리하는 꼭짓점의 모음이다. k-정점 연결 그래프는 ''k''개 미만의 꼭짓점을 제거해도 항상 나머지 그래프가 연결된 상태로 유지되는 그래프이다.

그래프는 어떤 꼭짓점을 다른 꼭짓점으로 매핑하는 대칭성을 가지면 정점-추이라고 한다. 그래프 열거와 그래프 동형의 맥락에서 '''레이블된 꼭짓점'''과 '''레이블되지 않은 꼭짓점'''을 구별하는 것이 중요하다. 레이블된 꼭짓점은 다른 레이블된 꼭짓점과 구별할 수 있도록 추가 정보가 연관된 꼭짓점이다. 두 그래프는 꼭짓점 간의 대응이 동일한 레이블을 가진 꼭짓점을 쌍으로 묶는 경우에만 동형으로 간주될 수 있다. 레이블되지 않은 꼭짓점은 그래프의 인접성만을 기반으로 다른 꼭짓점으로 대체될 수 있으며, 추가 정보를 기반으로 하지 않는다.

그래프의 꼭짓점은 다면체의 꼭짓점과 유사하지만 동일하지는 않다. 다면체의 골격은 그래프를 형성하며, 그 꼭짓점은 다면체의 꼭짓점이지만, 다면체 꼭짓점은 그래프 이론에서 존재한다고 가정하지 않는 추가 구조(기하학적 위치)를 갖는다. 다면체의 꼭짓점의 꼭짓점 도형은 그래프의 꼭짓점의 이웃과 유사하다.

3. 1. 독립 집합 (Independent Set)

독립 집합은 그래프에서 어떤 두 꼭짓점도 서로 인접하지 않은 꼭짓점들의 집합이다.[1]

3. 2. 꼭짓점 덮개 (Vertex Cover)

독립 집합은 그래프에서 서로 인접하지 않은 꼭짓점들의 집합이며, 꼭짓점 덮개는 그래프의 각 변이 적어도 하나의 꼭짓점과 연결되도록 하는 꼭짓점들의 집합이다.[1]

3. 3. 꼭짓점 공간 (Vertex Space)

그래프의 꼭짓점 공간은 그래프의 꼭짓점에 해당하는 기저 벡터 집합을 갖는 벡터 공간이다.[1]

4. 꼭짓점의 표현과 그래프의 종류



그래프에서 꼭짓점의 차수는 그 꼭짓점에 인접한 변의 개수를 의미하며, 𝛿(v)로 표기한다. 차수가 0인 꼭짓점은 '''고립 꼭짓점'''이라고 하며, 어떤 변의 끝점도 아니다. 차수가 1인 꼭짓점은 '''잎새 꼭짓점''' ('''펜던트 꼭짓점'''이라고도 함)이라고 한다.[1] 유향 그래프에서는 밖으로 나가는 변의 개수를 𝛿+(v)로 표기하는 밖차수, 들어오는 변의 개수를 𝛿−(v)로 표기하는 안차수로 구별할 수 있다. 안차수가 0인 꼭짓점은 '''소스 꼭짓점''', 밖차수가 0인 꼭짓점은 '''싱크 꼭짓점'''이다.

절단 꼭짓점은 제거하면 나머지 그래프가 분리되는 꼭짓점이며, 꼭짓점 분리 집합은 제거하면 나머지 그래프를 작은 조각으로 분리하는 꼭짓점의 모음이다. k-정점 연결 그래프는 ''k''개 미만의 꼭짓점을 제거해도 항상 나머지 그래프가 연결된 상태로 유지되는 그래프이다. 독립 집합은 두 개의 꼭짓점이 서로 인접하지 않은 꼭짓점의 집합이고, 꼭짓점 덮개는 그래프의 각 변의 적어도 하나의 끝점을 포함하는 꼭짓점의 집합이다. 그래프의 꼭짓점 공간은 그래프의 꼭짓점에 해당하는 기저 벡터 집합을 갖는 벡터 공간이다.

그래프의 꼭짓점은 다면체의 꼭짓점과 유사하지만 동일하지는 않다. 다면체의 골격은 그래프를 형성하며, 그 꼭짓점은 다면체의 꼭짓점이지만, 다면체 꼭짓점은 그래프 이론에서 존재한다고 가정하지 않는 추가 구조(기하학적 위치)를 갖는다. 다면체의 꼭짓점의 꼭짓점 도형은 그래프 꼭짓점의 이웃과 유사하다.

4. 1. 레이블된 꼭짓점과 레이블되지 않은 꼭짓점

레이블된 꼭짓점은 추가 정보가 연관되어 있어 다른 레이블된 꼭짓점과 구별된다. 동형 그래프는 꼭짓점 간의 대응이 동일한 레이블을 가진 꼭짓점을 쌍으로 묶는 경우에만 인정된다.[1] 레이블되지 않은 꼭짓점은 그래프의 인접성만을 기반으로 다른 꼭짓점으로 대체될 수 있으며, 추가 정보는 고려되지 않는다.[1]

4. 2. 정점-추이 그래프(Vertex-transitive Graph)

그래프에서 임의의 꼭짓점을 다른 임의의 꼭짓점으로 매핑하는 대칭성이 존재하면 정점-추이 그래프라고 한다.[1] 이는 어떤 꼭짓점이든 다른 꼭짓점으로 대칭 이동이 가능하다는 의미이다.

5. 꼭짓점과 다른 도형과의 관계

그래프의 꼭짓점은 다면체의 꼭짓점과 유사하지만, 동일하지는 않다. 다면체의 골격은 그래프를 형성하며, 그 꼭짓점은 그래프의 꼭짓점이 된다. 하지만 다면체의 꼭짓점은 그래프 이론에서는 가정하지 않는 추가적인 구조(기하학적 위치)를 가진다.[1]

5. 1. 꼭짓점 도형 (Vertex Figure)

그래프의 꼭짓점은 다면체의 꼭짓점과 유사하지만 동일하지는 않다. 다면체의 골격은 그래프를 형성하며, 그 꼭짓점은 다면체의 꼭짓점이지만, 다면체 꼭짓점은 그래프 이론에서 존재한다고 가정하지 않는 추가 구조(기하학적 위치)를 갖는다.[1] 다면체에서 한 꼭짓점에 연결된 면들의 상대적인 위치 관계를 나타내는 도형인 꼭짓점 도형은 그래프에서 한 꼭짓점에 연결된 이웃 꼭짓점들의 관계와 유사하다.

참조

[1] 파일 Small Network.png
[2] 서적


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com