노노그램
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
노노그램은 가로 및 세로에 표시된 숫자를 힌트로 사용하여 격자 내의 칸을 채워 그림을 완성하는 퍼즐이다. 1987년 일본의 이시다 논과 니시오 테츠야가 각각 개발했으며, 닌텐도는 '피크로스'라는 이름으로 비디오 게임을 출시하여 인기를 얻었다. 노노그램은 각 숫자가 연속된 검은 칸의 개수를 나타내며, 숫자가 여러 개인 경우 숫자 사이에는 최소 한 칸 이상의 빈칸이 있어야 한다. 노노그램을 풀 때는 0과 최고값 처리, 좌우 채우기로 공통된 검은 칸 찾기 등의 전략을 사용하며, 확정된 칸을 바탕으로 추가 칸을 찾아나간다. 때로는 가정법을 사용하여 모순을 찾아 문제를 해결하기도 하며, 다색화, 삼각형 칸 등 다양한 변형이 존재한다.
더 읽어볼만한 페이지
- 논리 퍼즐 - 웨이슨 선택 과제
웨이슨 선택 과제는 논리적 추론 능력을 평가하기 위해 규칙을 검증하는 데 필요한 카드 선택을 묻는 문제이며, 사회적 맥락에 따라 정답률이 달라지는 특징을 보인다. - 논리 퍼즐 - 기어큐브
기어큐브는 톱니바퀴처럼 맞물린 면으로 구성되어 180° 단위로 회전하는 3차원 퍼즐로, 90° 회전이 불가능하며 6개의 중심 조각과 54개의 기어를 가지고 41,472가지 상태를 나타내며 싱마스터 표기법을 사용하는 WCA 공식 큐브이다. - NP-완전 문제 - 지뢰 찾기
지뢰 찾기는 격자 형태 지뢰밭에서 지뢰를 피해 안전한 칸을 모두 여는 퍼즐 비디오 게임으로, 칸을 열어 지뢰 유무를 확인하며, 윈도우 탑재를 통해 대중화되었고 NP-완전 문제로 분류된다. - NP-완전 문제 - 스도쿠
스도쿠는 9x9 칸에 1부터 9까지의 숫자를 채워 넣는 퍼즐로, 각 가로줄, 세로줄, 3x3 칸에 숫자가 중복 없이 들어가야 하며, 레온하르트 오일러의 라틴 방진을 기반으로 다양한 변형과 응용 연구가 진행되고 있다.
| 노노그램 | |
|---|---|
| 개요 | |
| 다른 이름 | Griddler 그리들러 Hanjie 한지에 Paint by Numbers 페인트 바이 넘버스 Picross 피크로스 Pic-a-Pix 피크-어-픽스 |
| 유형 | 논리 퍼즐 |
| 풀이 방법 | 논리적 추론 |
| 역사 | |
| 발명가 | 石田 碩 (いしだ のぶお) (이시다 노부오) - 일본 西尾 徹也 (にしお てつや) (니시오 테츠야) - 일본 |
| 최초 등장 | 1987년 (일본) |
| 출판사 | 学研 (がっけん) (각켄) - 일본 Dell Magazines 델 매거진 - 미국 |
| 특징 | |
| 목표 | 힌트를 사용하여 숨겨진 그림을 찾는 것 |
| 규칙 | 숫자 힌트를 바탕으로 격자(Grid)를 칠하거나 비워 그림을 완성 |
| 필요 기술 | 논리 패턴 인식 |
| 변형 | 멀티플 피크로스 트라이어ングル 피크로스 (Triangle Picross) 컬러 피크로스 |
| 어원 | |
| 이름 유래 | "Nonogram"은 "Non-ogram"에서 유래, 노노 이시카와의 이름에서 따옴 |
| 일본어 명칭 | |
| 명칭 | お絵かきロジック (오에카키 로짓쿠) |
| 로마자 표기 | Oekaki Logic (오에카키 로짓쿠) |
| 의미 | 그림 그리기 논리 |
| 한국어 명칭 | |
| 명칭 | 노노그램 |
2. 역사
1987년, 일본의 그래픽 편집자 이시다 논은 켜지거나 꺼진 고층 빌딩 조명을 사용하여 격자 그림을 디자인하여 도쿄에서 열린 대회에서 우승했다. 이로 인해 그녀는 격자 안의 특정 사각형을 채우는 것을 기반으로 하는 퍼즐에 대한 아이디어를 얻었다. 이시다의 사고 과정의 일부는 그녀의 저서인 '노노구람'에서 볼 수 있다.[20] 한편, 일본의 전문 퍼즐 제작자인 니시오 테츠야는 이시다 논과는 별개로 독자적으로 노노그램과 유사한 퍼즐을 발명하여 다른 잡지에 게재했다. 니시오는 매트릭스(표 작성)를 사용한 로직 퍼즐의 매트릭스를 이용하여 그림을 그리는 것을 생각했다. 일반적인 로직 퍼즐에서는 매트릭스에 조건에 해당하는지 ○ 또는 ×를 채우지만, 이 ○와 ×를 검은 칸과 흰 칸으로 바꾸는 것을 생각하고, 힌트를 내는 방법을 고안하여 현재의 규칙을 완성했다. 이처럼 두 사람이 독자적인 과정을 거쳐 우연히 같은 형식의 문제로 귀결되었다. 후에 니시오는 문제를 제공하고 있는 『퍼즐러』지에서, 이시다는 퍼즐의 연재를 하고 있던 『사회신보』지에서 문제를 발표하게 되는데, 우연히도 양지의 발행일은 모두 1988년 7월 2일이었다.
노노그램은 가로와 세로에 적힌 숫자를 힌트로 하여 빈칸을 채워 그림을 완성하는 퍼즐이다. 각 숫자는 연속으로 칠해야 하는 검은 칸의 개수를 의미한다. 숫자와 숫자 사이에는 적어도 한 칸 이상의 빈칸이 있어야 한다. 숫자의 순서는 검은 칸이 칠해지는 순서와 일치해야 한다.
1988년, 이시다 논은 일본에서 "윈도우 아트 퍼즐"이라는 이름으로 세 개의 그림 격자 퍼즐을 출판했다. 1990년, 영국의 제임스 달게티는 이시다 논의 이름을 따서 노노그램이라는 이름을 발명했고, 더 선데이 텔레그래프는 매주 노노그램을 게재하기 시작했다.[2] 마이니치 신문의 일요판에서도 '''노노구람'''으로 명명되어 연재되었다(2006년 현재, 연재 종료). 1993년까지, 이시다 노노는 일본에서 첫 번째 노노그램 책을 출판했다. 세계문화사에서 『퍼즐러』 별책으로 단행본 『그림 그리기 로직 vol.1』[21]을 발매하여, 20만 부를 판매했다. 이에 편승한 유사 서적이 여러 권 출판되는 등, 그림 그리기 로직의 인기 몰이에 불을 지폈다고 말해진다.[22] 또한, '''그림 그리기 로직'''의 명칭은 세계문화사의 등록 상표가 되어 있으며[23], 동명의 퍼즐지가 간행되고 있다.[24] ''더 선데이 텔레그래프''는 "노노그램의 책"이라는 제목의 전용 퍼즐 책을 출판했다. 노노그램은 스웨덴, 미국 (원래는 ''게임스'' 잡지에서[3]), 남아프리카 공화국 및 기타 국가에서도 출판되었다. ''더 선데이 텔레그래프''는 1998년에 퍼즐의 새로운 이름을 선택하기 위한 대회를 열었다. 그리들러가 독자들이 선택한 우승 이름이었다.
1994년 10월에는, 일본문예사가 전문지인 『일러스트 로직』지를 창간했고[25], 학습연구사도 1995년 4월에 전문지를 창간했다.[22] 숫자 그림 맞추기는 네덜란드에서는 사노마 위트게버스(Sanoma Uitgevers)에서, 영국에서는 퍼즐러 미디어(Puzzler Media, 이전의 브리티시 유러피언 어소시에이티드 퍼블리셔스)에서, 이스라엘에서는 니쿠이 로시 퍼즐(Nikui Rosh Puzzles)에서 출판되었다. 노노그램 퍼즐이 실린 잡지는 미국, 영국, 독일, 네덜란드, 이탈리아, 헝가리, 핀란드, 체코, 슬로바키아, 러시아, 우크라이나 및 다른 많은 국가에서 출판된다.
1995년, 닌텐도는 '피크로스'라는 이름으로 노노그램 비디오 게임을 출시하여 전 세계적으로 큰 인기를 얻었다. 닌텐도는 라는 이름으로 여러 개의 노노그램 비디오 게임을 출시했다. 게임보이 게임 ''마리오의 피크로스''(Mario's Picross)는 1995년 3월 14일 일본에서 처음 출시되어 상당한 성공을 거두었다. ''피크로스 2''는 나중에 게임보이용으로, ''마리오의 슈퍼 피크로스''(Mario's Super Picross)는 슈퍼 패미컴용으로 출시되었지만, 미국 시장에는 번역되지 않았다(''마리오의 슈퍼 피크로스''는 2007년 9월 14일 Wii 버추얼 콘솔의 PAL 서비스에서 하나비 페스티벌의 일부로, 2020년 9월 23일 전 세계적으로 Nintendo Switch Online 서비스를 통해 출시되었다[11]). 두 게임 모두 와리오가 마리오의 숙적 역할을 하는 ''와리오의 피크로스''(Wario's Picross)를 선보였다. 닌텐도는 또한 일본 닌텐도 파워 주변 장치에 8개의 ''피크로스'' 볼륨을 출시했는데, 이를 ''NP 피크로스''라고 부르며, 각 볼륨에는 마리오, 젤다의 전설, 포켓몬 등 다양한 닌텐도 캐릭터를 기반으로 한 퍼즐을 포함한 새로운 퍼즐 세트가 포함되어 있다.
닌텐도는 2007년 닌텐도 DS 휴대용 시스템용으로 ''피크로스 DS''(Picross DS)를 출시했다. 이후 가장 많은 피크로스 게임 개발사 중 하나는 주피터 코퍼레이션으로, 2007년 닌텐도 DS용 ''피크로스 DS'', 닌텐도 3DS eShop용 ''피크로스 e'' 시리즈 8편(포켓몬, 젤다 및 산리오 캐릭터를 특징으로 하는 캐릭터별 타이틀 5편 포함), 닌텐도 스위치용 ''피크로스 S'' 시리즈 9편(각각 케모노 프렌즈와 오버로드를 특징으로 하는 캐릭터별 타이틀 2편과 세가의 마스터 시스템 및 제네시스의 지적 재산을 특징으로 하는 또 다른 타이틀 포함)을 출시했다.
1996년에는 일본 아케이드 게임 ''Logic Pro''가 Deniam Corp에서 출시되었고, 이듬해 속편이 출시되었다. 영국의 게임 개발사 Jagex는 2011년에 자사의 롤플레잉 게임인 ''룬스케이프''의 연례 할로윈 이벤트의 일환으로 노노그램 퍼즐을 출시했다. 2013년, Casual Labs는 미술관 복원이라는 테마로 이러한 퍼즐의 모바일 버전을 ''Paint it Back''이라는 이름으로 출시했다. 2017년 초에 출시된 ''Pictopix''는 Rock, Paper, Shotgun에 의해 PC에서 피크로스의 가치 있는 후계자로 제시되었다.[4] 다른 회사들도 노노그램 비디오 게임을 출시했다. 예를 들어 iOS의 Falcross[18], Microsoft Windows 및 Apple macOS의 Knitwit Studios의 Across-Stitch, 닌텐도 DS, Microsoft Windows 및 iOS의 Little Worlds Studio의 Color Cross 시리즈 게임 등이 있다. 또한 노노그램 퍼즐은 Deadly Rooms of Death의 다섯 번째 작품인 ''The Second Sky''와 같은 비피크로스 퍼즐 게임에도 등장했다.
3. 기본 규칙
'''숫자가 하나인 경우'''
1개의 숫자는 연속해서 검게 칠하는 칸(이하 ‘검은 칸’)의 수를 나타내고 있다. 단, 위치까지 나타내고 있는 것은 아니다.3
에 대해서는 다음의 3개의 가능성을 생각할 수 있다.3 3 3
'''숫자가 여러 개인 경우'''
노노그램에서 숫자가 여러 개인 경우, 각 숫자는 연속된 검은 칸의 개수를 나타낸다. 숫자 사이에는 최소 한 칸 이상의 빈 칸이 있어야 한다. 숫자의 순서는 검은 칸의 순서를 나타낸다.
예를 들어, '1 1'이 가로줄에 주어지면, 6가지 경우의 수가 나올 수 있다.
만약 '1 1 1'이 주어진다면, 가능한 경우는 한 가지뿐이다.
'3 1'과 '1 3'이 가로줄에 주어지면, 검은 칸의 순서에 따라 다음과 같은 해답이 나온다.
세로줄의 경우에도 마찬가지로 적용된다. 예를 들어, 세로줄에 '2 1'이 주어지면, 3가지 경우의 수가 나올 수 있다.
퍼즐을 풀기 위해서는 어떤 칸이 채워질 칸이고, 어떤 칸이 비어 있을 칸인지 결정해야 한다. 퍼즐을 푸는 사람들은 종종 논리적으로 확정된 공간을 표시하기 위해 점이나 십자표를 사용한다. 논리로 결정할 수 있는 칸은 채워져야 한다. 추측이 사용되면 단 하나의 오류가 전체 필드로 퍼져나가 솔루션을 완전히 망칠 수 있다. 오류는 때때로 한참 후에야 드러나 퍼즐을 수정하기가 매우 어려워진다. 숨겨진 그림이 오류를 찾아 제거하는 데 도움이 될 수 있지만, 오해의 소지가 있을 수 있으므로 퍼즐을 푸는 과정에서는 거의 역할을 하지 않는다.
많은 퍼즐은 한 번에 하나의 행이나 열에 대해서만 추론한 다음, 다른 행이나 열을 시도하고, 퍼즐이 완료될 때까지 반복하여 풀 수 있다. 더 어려운 퍼즐은 여러 행(또는 열)을 포함하는 여러 유형의 "만약?" 추론도 필요할 수 있다. 이는 모순을 찾는 방식으로 작동한다. 예를 들어, 어떤 칸이 오류를 발생시키기 때문에 채워질 수 없을 경우, 그 칸은 반드시 비어 있어야 한다.
3. 1. 숫자가 하나인 경우
1개의 숫자는 연속해서 검게 칠하는 칸(이하 ‘검은 칸’)의 수를 나타내고 있다. 단, 위치까지 나타내고 있는 것은 아니다.
| 3 |
에 대해서는 다음의 3개의 가능성을 생각할 수 있다.
| 3 | |||||||
| 3 | |||||||
| 3 |
3. 2. 숫자가 여러 개인 경우
노노그램에서 숫자가 여러 개인 경우, 각 숫자는 연속된 검은 칸의 개수를 나타낸다. 숫자 사이에는 최소 한 칸 이상의 빈 칸이 있어야 한다. 숫자의 순서는 검은 칸의 순서를 나타낸다.예를 들어, '1 1'이 가로줄에 주어지면, 6가지 경우의 수가 나올 수 있다.
만약 '1 1 1'이 주어진다면, 가능한 경우는 한 가지뿐이다.
'3 1'과 '1 3'이 가로줄에 주어지면, 검은 칸의 순서에 따라 다음과 같은 해답이 나온다.
세로줄의 경우에도 마찬가지로 적용된다. 예를 들어, 세로줄에 '2 1'이 주어지면, 3가지 경우의 수가 나올 수 있다.
4. 풀이 전략
노노그램을 풀기 위한 전략은 다음과 같다.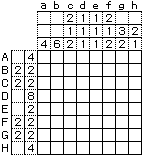
- 왼쪽 8×8 칸 문제를 예로 퍼즐 전체의 흐름을 나타낸다. 편의상 가로줄은 대문자 A부터 H, 세로줄은 소문자 a부터 h를 사용하여 부르고, 특정 칸은 가로줄과 세로줄의 이름을 나란히 불러 표시한다(가장 왼쪽 위의 칸은 Aa가 된다). 또한, 빨간색으로 표시된 칠해진 부분과 × 표시는 '''가로줄 숫자'''에서, 파란색은 '''세로줄 숫자'''에서 유도된 것을 나타낸다.
- D열 "8"은 최고값이므로, 해당 열은 모두 칠할 수 있다('''0과 최고값 처리''' ).
- b열 "6", c열 "2,1,2", f열 "2,1,2"는, '''좌우로 붙였을 때 생기는 공통의 검은 칸을 처리''' 하는 정석에서 일부 칠할 수 있다.
- a열 "4" 중 검은색이 확정된 Da의 칸에서 생각하여, 최하단 Ha는 흰색 칸임이 확정된다('''확실하게 검은 칸이 닿는 칸, 닿지 않는 칸을 처리''' ).
- g열 "3,2" 중 검은 칸Dg의 위치에서 생각해 볼 때, 분명히 "3"에 기인하는 검은 칸이다. 따라서, 이 열의 최상단 Ag는 흰색 칸임이 확정된다.
- c열 "2,1,2"에 대해, Bc, Dc의 검은 칸은 위치로 보아 각각 "2", "1"에 기인하는 것을 알 수 있다. 따라서, Dc의 위아래 양 옆은 흰색 칸으로 결정된다('''검은 칸의 양 옆을 막는 처리''' ). 또한, 그로 인해 최상단 Ac가 검은 칸임도 확정된다('''가장자리와 최고값 갱신에 대한 처리''' ).
- f열도 c열과 유사한 처리를 할 수 있다.
- A열 "4"에 있는 2개의 검은 칸 Ac, Af는 당연히 같은 "4"에 기인한다. 따라서, 그 사이의 2칸은 검은 칸으로 결정되며, '''전체 검은 칸, 전체 흰 칸이 확정된 열 처리''' 를 할 수 있다.
- B열 "2,2"는 둘 다 '''확실하게 검은 칸이 닿는 칸, 닿지 않는 칸을 처리''' 하는 정석에서 양 끝의 칸 Ba, Bh가 흰색 칸으로 결정된다. G열도 마찬가지이다.
- C열 "2,2"는 Cc가 흰색 칸으로 확정되었기 때문에, '''가장자리와 최고값 갱신에 대한 처리''' 에서 Ca가 검은 칸임이 확정된다.
- E열 "2"는 Ec가 흰색 칸으로 확정되었기 때문에, 이 역시 Ea가 검은 칸임이 확정된다. 그 후, '''전체 검은 칸, 전체 흰 칸이 확정된 열 처리''' 를 할 수 있다.
- H열 "4"도 '''가장자리와 최고값 갱신에 대한 처리''' 에서 검은 칸 하나가 확정된다.
- a열의 모든 칸이 확정된다.
- b열 "6"은 '''가장자리와 최고값 갱신에 대한 처리''' 에서 검은 칸 하나가 확정된다.
- d열 "1,1,1"에는 '''검은 칸의 양 옆을 막는 처리''' 를 할 수 있다.
- e열의 모든 칸이 확정된다.
- g열의 "3"이 확정, "2"가 일부 확정된다.
- h열의 "2"가 확정이다.
- B열의 모든 칸이 확정된다.
- F열 "2,2"는, '''검은 칸의 양 옆을 막는 처리''' 에서 Fc가 흰색 칸으로 결정되며, Fd는 '''협소한 칸 처리''' 가 가능하여 흰색 칸으로 확정된다. 그 후, '''가장자리와 최고값 갱신에 대한 처리''' 에서 Fg가 검은 칸이 된다.
- G열의 모든 칸이 확정된다.
- b, c, g열의 모든 칸이 확정된다.
- H열의 모든 칸이 확정된다.
- f, h열의 모든 칸이 확정되어 완성된다.
- 완성도( 소문자의 알파벳 "e" 문자)
- 이상의 예에서 알 수 있듯이, 풀 때는 자주 "이 검은 칸은 어떤 숫자에 기인하는가"하는 것이 중요해진다.
== 첫 번째 단계: 확정적인 칸 찾기 ==
노노그램을 풀 때, 처음에는 아무 단서가 없는 상태이므로 단서 없이도 확정할 수 있는 칸부터 찾아야 한다. 이 작업을 빠뜨리면 중간에 막힐 수 있으므로 주의해야 한다.
- '''0과 최고값 처리:''' 0이 적힌 줄은 모두 빈칸이고, 최고값이 적힌 줄은 모두 검은 칸이다. 예를 들어, 최고값이 10인 경우, 10이 적힌 줄은 모두 검은 칸으로 채운다. 빈칸이 확정된 칸에는 × 표시를 하여 구분하는 것이 좋지만, 너무 크게 표시하면 완성된 그림이 보기 흉해지므로 주의한다.
- '''더해서 최고값이 되는 경우:''' 숫자 사이에 빈칸을 하나씩만 넣었을 때 최고값이 되는 경우는 한 가지 경우밖에 없다. 예를 들어, 7과 2가 주어지고 최고값이 10인 경우, 7+1+2=10이므로, 숫자 사이에 빈칸을 하나씩 넣고 나머지는 검은 칸으로 채운다. 숫자가 작을수록 알아채기 어려우므로 주의해야 한다. 예를 들어, 4, 2, 2는 4+1+2+1+2=10, 1, 2, 1, 1, 1은 1+1+2+1+1+1+1+1+1=10이므로 같은 방식으로 처리한다.
- '''좌우 채우기로 공통된 검은 칸 찾기:''' 숫자를 왼쪽 끝과 오른쪽 끝에 붙여서 칠했을 때 공통으로 칠해지는 칸은 검은 칸으로 확정한다. 예를 들어, 8이 주어지면, 왼쪽 끝과 오른쪽 끝에 8칸을 칠했을 때 가운데 6칸은 항상 칠해지므로 검은 칸으로 확정한다. 6이 주어지면, 왼쪽과 오른쪽에 6칸을 칠했을 때 가운데 2칸이 공통되므로 검은 칸으로 확정한다.
- 여러 숫자가 있는 경우에도, 숫자 사이에 빈칸을 한 칸씩 넣고 같은 작업을 할 수 있다. 단, 왼쪽과 오른쪽에서 칠했을 때 공통되는 부분이 있어도, 다른 숫자에서 온 경우에는 공통되었다고 볼 수 없다. 예를 들어, 4와 2가 주어지면, 왼쪽에서 칠했을 때는 4칸과 2칸이 겹치지만, 오른쪽에서 칠했을 때는 2칸과 4칸이 겹치므로, 4칸에 해당하는 부분만 확정된다.
- 블록을 다른 행/열과 독립적으로 채우기 위해 수학적 기법을 사용하면 퍼즐을 시작하는데 도움이 된다.
1. 단서를 모두 더하고 그 사이에 있는 각 "공백"에 대해 1을 더한다.
2. 이 숫자를 행에서 사용 가능한 총 수에서 뺀다.
3. 2단계의 숫자보다 큰 단서는 일부 블록이 채워진다.
4. 3단계의 각 단서에 대해 2단계의 숫자를 빼서 채울 수 있는 블록 수를 결정한다.
5. 블록을 채우려면 블록이 모두 한쪽으로 밀려 있다고 가정하고 해당 측면에서 블록 "통과"를 계산하고 적절한 수의 블록을 다시 채웁다. 이것은 양방향에서 수행할 수 있다.
6. 3단계에서 식별된 모든 단서에 대해 5단계를 반복한다.
== 두 번째 단계: 확정된 칸을 이용해 추가 칸 찾기 ==
첫 번째 단계에서 확정된 칸을 바탕으로 추가로 칸을 확정짓는 단계이다. 이 단계에서 확정된 칸은 다시 새로운 단서가 되어, 퍼즐을 모두 풀 때까지 반복된다. 이미 확정된 검은 칸은 갈색 칸, 확정된 빈칸은 갈색 ×, 새롭게 확정된 검은 칸과 빈칸은 각각 검은 칸과 검은 ×로 표시한다.
- '''모든 검은 칸/빈칸 확정된 열 처리:''' 검은 칸의 수가 숫자의 합과 일치하면 나머지 칸은 모두 빈칸으로 확정한다. 빈칸과 검은 칸의 합이 숫자의 합과 일치하면 나머지 칸은 모두 검은 칸으로 확정한다.
(예시 1)
| 1 |
숫자 '1'에 대해 이미 하나의 검은 칸이 확정되어 있으므로, 나머지 칸은 모두 빈칸이다.
| 1 | × | × | × | × | × | × | × | × | × |
(예시 2)
| 1 | 1 | 1 | 1 |
검은 칸 4개가 필요하므로, 빈칸을 제외한 나머지 칸은 모두 검은 칸이다.
| 1 | 1 | 1 | 1 |
- '''검은 칸 이웃 칸 처리:''' 검은 칸이 연속되는 것이 확실하면 그 양옆 칸은 빈칸으로 확정한다.
(예시 1)
| 1 | 2 | 1 |
이미 칠해진 검은 칸은 '2'에서 온 것이 확실하므로, 숫자 사이 빈칸을 고려하여 양옆을 빈칸으로 확정한다.
| 1 | 2 | 1 | × | × |
(예시 2)
| 1 | 2 | 1 |
이미 확정된 칸이 '1'에서 온 것인지 '2'에서 온 것인지 불확실하므로, 추가 확정은 불가능하다.
- '''가장자리 처리:''' 가장 바깥쪽 칸이 확정되면 해당 숫자가 나타내는 검은 칸은 확정된다.
(예시 1)
| 3 | 2 |
가장 왼쪽이 확정되었으므로, '3'이 나타내는 칸은 다음과 같이 확정된다.
| 3 | 2 | × |
왼쪽에서 네 번째 칸에 ×를 추가하는 것은 '검은 칸 이웃 칸 처리'에 따른 것이다.
(예시 2)
| 3 | 2 |
가장 오른쪽이 확정되었으므로, '2'가 나타내는 칸은 다음과 같이 확정된다.
| 3 | 2 | × |
오른쪽에서 세 번째 칸 ×는 '검은 칸 이웃 칸 처리'에 따른 것이다.
- '''협소한 칸 처리:''' 연속해서 칠할 수 있는 칸 수가 숫자보다 적으면 해당 칸은 빈칸으로 확정한다.
(예시 1)
| 3 |
오른쪽 끝에서 검은 칸을 채우면 2칸밖에 채울 수 없으므로, 오른쪽 끝 두 칸은 빈칸이다.
| 3 | × | × |
(예시 2)
| 3 |
×와 × 사이에는 2칸밖에 채울 수 없으므로, 해당 칸은 빈칸이다.
| 3 | × | × |
- '''확실히 검은 칸이 닿는/닿지 않는 칸 처리:''' 검은 칸이 확정되어 있고, 숫자를 고려했을 때 닿지 않는 칸은 빈칸으로 확정하고, 아무리 가장자리에 붙여도 검은 칸이 튀어나오는 부분은 검은 칸으로 확정한다.
(예시 1)
| 2 |
가능성은 다음 두 가지뿐이므로,
| 2 | |||||||||||||||||
| 2 |
다음과 같이 확정한다.
| 2 | × | × | × | × | × | × | × |
(예시 2)
| 5 |
오른쪽 끝에서 검은 칸을 가져와도 오른쪽에서 5번째 칸은 검은 칸이다. 확정된 칸에서 왼쪽으로 5칸을 해도 왼쪽에서 3번째 칸까지는 닿지 않는다.
| 5 | × | × | × |
(예시 3)
| 3 | 4 |
오른쪽 검은 칸에서 왼쪽으로 4칸을 늘려도 두 검은 칸은 이어지지 않는다. 사이에는 최소 1개의 빈칸이 필요하므로, 왼쪽에서 4번째 칸은 4의 칸으로 채울 수 없다. 4의 왼쪽 끝이 오른쪽으로 이동하므로(왼쪽에서 5번째 칸), 거기에서 오른쪽으로 4번째 칸은 검은 칸이다.
| 3 | 4 |
- '''가장자리나 최고값 갱신에 대한 처리:''' 바깥쪽 빈칸이 연속으로 확정되면 가장자리가 안쪽으로 이동한 것으로 간주하여 최고값을 갱신하고, 이를 이용해 추가 칸을 확정한다.
(예시 1)
| 5 |
1단계에서는 확정할 수 없었지만,
| 5 |
로 확정하면, 오른쪽 끝이 안쪽으로 이동한 것으로 간주, 오른쪽에서 두 번째 칸을 새 오른쪽 끝으로 생각하여 '좌우에 채울 때 생기는 공통된 검은 칸 처리'를 진행한다
4. 1. 첫 번째 단계: 확정적인 칸 찾기
노노그램을 풀 때, 처음에는 아무 단서가 없는 상태이므로 단서 없이도 확정할 수 있는 칸부터 찾아야 한다. 이 작업을 빠뜨리면 중간에 막힐 수 있으므로 주의해야 한다.- 0과 최고값 처리: 0이 적힌 줄은 모두 빈칸이고, 최고값이 적힌 줄은 모두 검은 칸이다. 예를 들어, 최고값이 10인 경우, 10이 적힌 줄은 모두 검은 칸으로 채운다. 빈칸이 확정된 칸에는 × 표시를 하여 구분하는 것이 좋지만, 너무 크게 표시하면 완성된 그림이 보기 흉해지므로 주의한다.
- 더해서 최고값이 되는 경우: 숫자 사이에 빈칸을 하나씩만 넣었을 때 최고값이 되는 경우는 한 가지 경우밖에 없다. 예를 들어, 7과 2가 주어지고 최고값이 10인 경우, 7+1+2=10이므로, 숫자 사이에 빈칸을 하나씩 넣고 나머지는 검은 칸으로 채운다. 숫자가 작을수록 알아채기 어려우므로 주의해야 한다. 예를 들어, 4, 2, 2는 4+1+2+1+2=10, 1, 2, 1, 1, 1은 1+1+2+1+1+1+1+1+1=10이므로 같은 방식으로 처리한다.
- 좌우 채우기로 공통된 검은 칸 찾기: 숫자를 왼쪽 끝과 오른쪽 끝에 붙여서 칠했을 때 공통으로 칠해지는 칸은 검은 칸으로 확정한다. 예를 들어, 8이 주어지면, 왼쪽 끝과 오른쪽 끝에 8칸을 칠했을 때 가운데 6칸은 항상 칠해지므로 검은 칸으로 확정한다. 6이 주어지면, 왼쪽과 오른쪽에 6칸을 칠했을 때 가운데 2칸이 공통되므로 검은 칸으로 확정한다.
- 여러 숫자가 있는 경우에도, 숫자 사이에 빈칸을 한 칸씩 넣고 같은 작업을 할 수 있다. 단, 왼쪽과 오른쪽에서 칠했을 때 공통되는 부분이 있어도, 다른 숫자에서 온 경우에는 공통되었다고 볼 수 없다. 예를 들어, 4와 2가 주어지면, 왼쪽에서 칠했을 때는 4칸과 2칸이 겹치지만, 오른쪽에서 칠했을 때는 2칸과 4칸이 겹치므로, 4칸에 해당하는 부분만 확정된다.
- 블록을 다른 행/열과 독립적으로 채우기 위해 수학적 기법을 사용하면 퍼즐을 시작하는데 도움이 된다.
1. 단서를 모두 더하고 그 사이에 있는 각 "공백"에 대해 1을 더한다.
2. 이 숫자를 행에서 사용 가능한 총 수에서 뺀다.
3. 2단계의 숫자보다 큰 단서는 일부 블록이 채워진다.
4. 3단계의 각 단서에 대해 2단계의 숫자를 빼서 채울 수 있는 블록 수를 결정한다.
5. 블록을 채우려면 블록이 모두 한쪽으로 밀려 있다고 가정하고 해당 측면에서 블록 "통과"를 계산하고 적절한 수의 블록을 다시 채웁다. 이것은 양방향에서 수행할 수 있다.
6. 3단계에서 식별된 모든 단서에 대해 5단계를 반복한다.
4. 2. 두 번째 단계: 확정된 칸을 이용해 추가 칸 찾기
첫 번째 단계에서 확정된 칸을 바탕으로 추가로 칸을 확정짓는 단계이다. 이 단계에서 확정된 칸은 다시 새로운 단서가 되어, 퍼즐을 모두 풀 때까지 반복된다. 이미 확정된 검은 칸은 갈색 칸, 확정된 빈칸은 갈색 ×, 새롭게 확정된 검은 칸과 빈칸은 각각 검은 칸과 검은 ×로 표시한다.- 모든 검은 칸/빈칸 확정된 열 처리: 검은 칸의 수가 숫자의 합과 일치하면 나머지 칸은 모두 빈칸으로 확정한다. 빈칸과 검은 칸의 합이 숫자의 합과 일치하면 나머지 칸은 모두 검은 칸으로 확정한다.
(예시 1)
| 1 |
숫자 '1'에 대해 이미 하나의 검은 칸이 확정되어 있으므로, 나머지 칸은 모두 빈칸이다.
| 1 | × | × | × | × | × | × | × | × | × |
(예시 2)
| 1 | 1 | 1 | 1 |
검은 칸 4개가 필요하므로, 빈칸을 제외한 나머지 칸은 모두 검은 칸이다.
| 1 | 1 | 1 | 1 |
- 검은 칸 이웃 칸 처리: 검은 칸이 연속되는 것이 확실하면 그 양옆 칸은 빈칸으로 확정한다.
(예시 1)
| 1 | 2 | 1 |
이미 칠해진 검은 칸은 '2'에서 온 것이 확실하므로, 숫자 사이 빈칸을 고려하여 양옆을 빈칸으로 확정한다.
| 1 | 2 | 1 | × | × |
(예시 2)
| 1 | 2 | 1 |
이미 확정된 칸이 '1'에서 온 것인지 '2'에서 온 것인지 불확실하므로, 추가 확정은 불가능하다.
- 가장자리 처리: 가장 바깥쪽 칸이 확정되면 해당 숫자가 나타내는 검은 칸은 확정된다.
(예시 1)
| 3 | 2 |
가장 왼쪽이 확정되었으므로, '3'이 나타내는 칸은 다음과 같이 확정된다.
| 3 | 2 | × |
왼쪽에서 네 번째 칸에 ×를 추가하는 것은 '검은 칸 이웃 칸 처리'에 따른 것이다.
(예시 2)
| 3 | 2 |
가장 오른쪽이 확정되었으므로, '2'가 나타내는 칸은 다음과 같이 확정된다.
| 3 | 2 | × |
오른쪽에서 세 번째 칸 ×는 '검은 칸 이웃 칸 처리'에 따른 것이다.
- 협소한 칸 처리: 연속해서 칠할 수 있는 칸 수가 숫자보다 적으면 해당 칸은 빈칸으로 확정한다.
(예시 1)
| 3 |
오른쪽 끝에서 검은 칸을 채우면 2칸밖에 채울 수 없으므로, 오른쪽 끝 두 칸은 빈칸이다.
| 3 | × | × |
(예시 2)
| 3 |
×와 × 사이에는 2칸밖에 채울 수 없으므로, 해당 칸은 빈칸이다.
| 3 | × | × |
- 확실히 검은 칸이 닿는/닿지 않는 칸 처리: 검은 칸이 확정되어 있고, 숫자를 고려했을 때 닿지 않는 칸은 빈칸으로 확정하고, 아무리 가장자리에 붙여도 검은 칸이 튀어나오는 부분은 검은 칸으로 확정한다.
(예시 1)
| 2 |
가능성은 다음 두 가지뿐이므로,
| 2 | |||||||||||||||||
| 2 |
다음과 같이 확정한다.
| 2 | × | × | × | × | × | × | × |
(예시 2)
| 5 |
오른쪽 끝에서 검은 칸을 가져와도 오른쪽에서 5번째 칸은 검은 칸이다. 확정된 칸에서 왼쪽으로 5칸을 해도 왼쪽에서 3번째 칸까지는 닿지 않는다.
| 5 | × | × | × |
(예시 3)
| 3 | 4 |
오른쪽 검은 칸에서 왼쪽으로 4칸을 늘려도 두 검은 칸은 이어지지 않는다. 사이에는 최소 1개의 빈칸이 필요하므로, 왼쪽에서 4번째 칸은 4의 칸으로 채울 수 없다. 4의 왼쪽 끝이 오른쪽으로 이동하므로(왼쪽에서 5번째 칸), 거기에서 오른쪽으로 4번째 칸은 검은 칸이다.
| 3 | 4 |
- 가장자리나 최고값 갱신에 대한 처리: 바깥쪽 빈칸이 연속으로 확정되면 가장자리가 안쪽으로 이동한 것으로 간주하여 최고값을 갱신하고, 이를 이용해 추가 칸을 확정한다.
(예시 1)
| 5 |
1단계에서는 확정할 수 없었지만,
| 5 |
로 확정하면, 오른쪽 끝이 안쪽으로 이동한 것으로 간주, 오른쪽에서 두 번째 칸을 새 오른쪽 끝으로 생각하여 '좌우에 채울 때 생기는 공통된 검은 칸 처리'를 진행한다.
| 5 |
(예시 2)
| 1 | 1 | 1 | 1 |
1단계에서는 확정할 수 없었지만,
| 1 | 1 | 1 | 1 |
로 확정하면, 최고값이 10에서 7로 줄어든 것으로 간주한다. 1+1+1+1+1+1+1=7이므로,
| 1 | 1 | 1 | 1 | × | × | × |
- 나눠진 칸 처리: 긴 빈칸의 중간이 흰 칸으로 확정되면, 그 좌우를 각각 독립적으로 처리할 수 있다.
(예)
| 3 | 3 |
1단계에서는 확정할 수 없었지만,
| 3 | 3 |
로 확정된 경우, 확정된 흰 칸 좌우 어느 한쪽에 모든 검은 칸이 들어갈 수 없으므로, 좌우 각각 1개씩 들어간다.
| 3 | 3 |
이 외에도 다양한 방법으로 추가적인 칸을 확정할 수 있다. 예를 들어, 공간의 중요성을 활용하여 큰 블록을 강제하거나, 너무 작은 간격을 공백으로 채우는 방법이 있다. 또한, 테두리 근처에 첫 번째 단서 길이보다 멀지 않은 상자가 있을 때, 첫 번째 단서가 해당 상자를 통과하여 바깥쪽으로 퍼져 나가는 방법을 활용할 수도 있다. 경우에 따라, 상자를 하나의 블록으로 합치거나, 공백으로 여러 블록으로 분할하는 방법을 사용할 수도 있다.
4. 3. 세 번째 단계: 고급 전략
위의 방법만으로 막힌 경우, 가정법(귀류법)을 사용할 수 있다. 이는 특정 칸을 검은 칸 또는 빈칸으로 가정하고 풀이를 진행하여 모순이 발생하는지 확인하는 방법이다. 모순이 발생하면 가정이 틀린 것이므로 해당 칸의 상태를 반대로 확정한다.[26]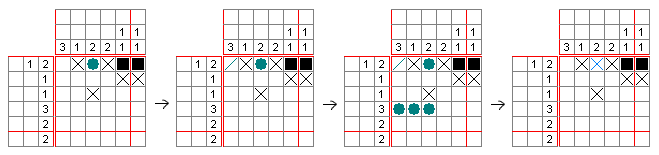
예를 들어, 첫 번째 행에 상자를 시도했는데, 이로 인해 해당 행의 시작 부분에 빈 칸이 생기는 경우가 있다. 그러면 빈 칸은 첫 번째 열에 상자를 "강제"하고, 이는 네 번째 행에 세 개의 상자 블록으로 "연결"된다. 그러나 세 번째 열에는 상자가 허용되지 않으므로 잘못된 것이다. 따라서 시도한 칸은 상자가 아니어야 하므로 빈 칸이어야 한다.[26]
| 2 | 2 | … | |||
| 2 | |||||
| 1 | |||||
| ⁝ |
왼쪽 위의 칸이 검은 칸이라고 가정한다.
| 2 | 2 | … | |
| 2 | × | ||
| 1 | |||
| ⁝ | × | × |
세로 열・가로 열의 2에 따라 칠해나가면, 1의 가로 열에 두 개의 검은 칸이 들어가 모순이 발생한다.
| 2 | 2 | … | |||
| 2 | × | ||||
| 1 | |||||
| ⁝ |
따라서, 왼쪽 위의 칸은 ×임을 알 수 있다.
이 방법은 모순이 발생하기까지의 전개가 길어 예측하기 힘들고, 고도의 훈련이 필요할 수 있다. 어떤 빈 칸을 먼저 시도해야 할지 빠르게 알 수 있는 방법이 없다는 문제도 있다. 일반적으로 몇 개의 칸만 진행을 유도하고, 다른 칸은 막다른 골목으로 이어진다.
가정을 사용하지 않으면 풀 수 없는 문제는 논리적으로 풀 수 없는 문제이므로 채용을 피하는 경향도 있다. 주피터가 발매하는 게임 소프트 『피크로스 e』 시리즈에서는, 모든 문제가 논리적으로 풀 수 있으며 가정을 필요로 하지 않는다고 미리 공지하고 있다.[27]
5. 다색화
기본 규칙으로는 흑백 그림만 그릴 수 없기 때문에 둘 이상의 색을 사용할 수 있게 한 규칙도 존재한다.
가장 일반적인 것은 숫자마다 색이 지정되어 있어서 숫자에 지정된 색으로 칠하는 것이다. 이 경우에 같은 열에 숫자가 둘 이상 있어도 다른 색이라면 사이에 공백이 들어가지 않아도 좋다는 규칙이 추가된다(같은 색이라면 기본 규칙처럼 한 칸 이상 비운다).
풀 때에는 아래의 내용에 주의할 필요가 있다.
- 숫자와 숫자 사이에 들어가지 않은 경우가 있기 때문에 확정된 칸이 적어진다.
- 각 색이 어떤 열에서 사용되고 있는지를 확인한다. 이것에 의해서 그 색으로 '''칠할 수 없는''' 범위가 나뉘며 그곳에서부터 결정되는 경우가 있다.
6. 문제 만들기
단순히 도트 그림을 그린다고 해서 노노그램 문제로 성립하는 것은 아니다. 답이 하나로 정해지지 않는 경우가 있기 때문이다. 컴퓨터 소프트웨어 중에는 문제 성립 여부를 자동으로 판정해 주는 기능이 있는 것도 있다.
7. 삼각형 칸
칠하는 칸을 정사각형을 비스듬히 자른 삼각형으로 한 규칙도 있다. 이러한 것을 ''다이아몬드 로직'' 또는 ''다이아 로직'' 등으로 불린다.[30][28]
8. 기타
큰 문제를 풀 때, 첫 번째 단계에서 칠할 수 있는 칸을 계산으로 구할 수 있다. 100×100칸 등 방대한 칸 수에서는 칠할 칸을 찾는 것이 매우 번거롭기 때문이다.
계산 방법은 다음과 같다.
- 먼저, 검은색 칸의 합계를 구한다. 즉, 구하고 싶은 행의 힌트에 나와 있는 숫자를 모두 더한다.
- 다음으로, 행의 힌트 개수에서 1을 뺀 수(검은색 칸 사이에 들어가는 흰색 칸의 합계의 최솟값)를 더한다.
- 마지막으로, 칠할 수 있는지 알고 싶은 검은색 칸의 수 B를 추가로 더한다. 우선, 행의 힌트 중 최댓값이 좋다.
이렇게 구한 수에서 행의 칸 수를 빼서 나온 수가, 힌트 B에 대해 제1단계의 방법으로 칠할 수 있는 칸의 수이다. 0 이하가 된 경우에는, 행의 수 B는 제1단계에서는 칠할 수 없다.
예를 들어 힌트가 6 2 3인 경우, 단서를 모두 더하고 그 사이에 있는 각 "공백"에 대해 1을 더한다. (6 + 1 + 2 + 1 + 3 = 13). 이 숫자를 행에서 사용 가능한 총 수에서 뺀다. (15 - 13 = 2). 2단계의 숫자보다 큰 단서는 일부 블록이 채워진다. 예제에서는 단서 6과 3에 적용되지만 2에는 적용되지 않는다. 3단계의 각 단서에 대해 2단계의 숫자를 빼서 채울 수 있는 블록 수를 결정한다. 예를 들어 6 단서는 (6 - 2 =) 4개의 블록이 채워지고 3 단서는 (3 - 2 =) 1개가 채워진다.
블록을 채우려면 블록이 모두 한쪽으로 밀려 있다고 가정하고 해당 측면에서 블록 "통과"를 계산하고 적절한 수의 블록을 다시 채운다.
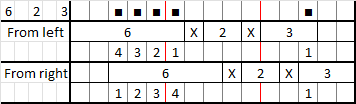
참조
[1]
서적
2007 IEEE Symposium on Computational Intelligence and Games
IEEE
2007-04
[2]
웹사이트
Origins of Cross Reference Grid & Picture Grid Puzzles
http://puzzlemuseum.[...]
2018-01-08
[3]
서적
Games Magazine Presents Paint by Numbers
https://books.google[...]
Random House
[4]
웹사이트
Wot I Think: Fantastic picross puzzler Pictopix
https://www.rockpape[...]
2017-01-12
[5]
간행물
NP-completeness results for NONOGRAM via Parsimonious Reductions
[6]
간행물
Playing Games: The complexity of Klondike, Mahjong, Nonograms and Animal Chess
http://www.liacs.nl/[...]
Leiden Institute of Advanced Computer Science, Leiden University
2012-06-29
[7]
논문
Acyclic Constraint Logic and Games
https://content.iosp[...]
2019-02-24
[8]
간행물
An algorithm reconstructing convex lattice sets
https://hal.archives[...]
[9]
웹사이트
Survey of Paint-by-Number Puzzle Solvers
http://webpbn.com/su[...]
2013-09-25
[10]
논문
Solving Nonograms by combining relaxations
[11]
Youtube
NES & Super NES - September Game Updates - Nintendo Switch Online
https://www.youtube.[...]
2020-09-15
[12]
웹사이트
Picross DS Review
http://www.ign.com/a[...]
2013-12-18
[13]
뉴스
Picross DS
http://www.thunderbo[...]
2013-12-18
[14]
웹사이트
Picross DS
http://www.eurogamer[...]
2013-12-18
[15]
문서
Harris
[16]
문서
McCarthy
[17]
웹사이트
Picross 3D Finally Getting a Sequel
http://www.kotaku.co[...]
2015-08-19
[18]
웹사이트
Falcross - Picross puzzles for iPhone and iPad
http://www.falcross.[...]
[19]
웹사이트
Triddlers rules and examples
https://www.griddler[...]
Griddlers.net
2010-01-01
[20]
서적
ののぐらむ―絵が出てくる数理パズル
https://www.nippyo.c[...]
日本評論社
[21]
서적
お絵かきロジック vol.1
https://www.amazon.c[...]
世界文化社
[22]
뉴스
日本生まれの新パズルが人気 お絵かきロジック
読売新聞
1995-11-24
[23]
문서
商標登録3067075
https://www.j-platpa[...]
[24]
웹사이트
「お絵かきロジック」世界文化社グループ|パズル誌
http://www.sekaibunk[...]
世界文化社
[25]
웹사이트
Fujisan.co.jp 雑誌「イラストロジック」
https://www.fujisan.[...]
fujisan.co.jp
[26]
웹사이트
アドバイス
https://www.nintendo[...]
VCマリオのスーパーピクロス
2022-08-22
[27]
웹사이트
ピクロスe3オフィシャルサイト
https://www.jupiter.[...]
ジュピター
2022-08-22
[28]
문서
たとえば日本文芸社の『イラストロジック』では「ダイヤロジック」の名で頻繁に出題している。
[29]
문서
History of Grid Puzzles
http://puzzlemuseum.[...]
2013-12-18
[30]
문서
예를 들면 일본 문예사의 “일러스트 로직”에서는 ‘다이아 로직’의 이름으로 빈번히 출제되고 있다.
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com