메르카토르 도법

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

메르카토르 도법은 1569년 게라르두스 메르카토르가 발표한 지도 투영법으로, 등각 항로를 직선으로 표현하여 해상 항해에 적합하도록 설계되었다. 위도에 따라 축척이 왜곡되는 특징이 있으며, 극지방으로 갈수록 면적이 과장되어 나타난다. 이러한 왜곡으로 인해 세계 지도의 부적합성 논란이 있었으며, 횡축 및 사축 메르카토르 도법과 같은 변형도 존재한다. 오늘날에는 웹 매핑 서비스와 해도 등에서 사용되고 있다.

더 읽어볼만한 페이지

지리학의 역사 - 대항해시대
대항해시대는 15세기부터 17세기까지 유럽 국가들이 새로운 항로를 개척하고 식민지를 건설하며 세계를 탐험한 시기로, 유럽의 영향력 확대를 가져왔지만 아메리카 원주민 문명 파괴, 노예 무역 등 부정적인 결과를 초래했다.
지리학의 역사 - 지구의 역사
지구의 역사는 약 46억 년 전 태양계 형성부터 시작하여 철 재앙, 달의 생성, 생명 탄생, 판 구조론, 대산소화 사건, 눈덩이 지구, 캄브리아기 대폭발, 공룡 번성, 포유류와 인류의 등장 등을 거치며 현재에 이르는 지구의 주요 사건과 진화를 포괄한다.
게라르두스 메르카토르 - 사축 메르카토르 도법
사축 메르카토르 도법은 메르카토르 도법의 사위 양상으로, 원통형 투영법, 정각도법 등의 특징을 가지며 좁은 폭의 지역에 대한 정확한 지도 제작에 사용되고, 핫틴 사위 메르카토르 도법은 여러 국가의 표준 지도 투영법으로 활용된다.
게라르두스 메르카토르 - 뒤스부르크-에센 대학교
뒤스부르크-에센 대학교는 독일 노르트라인-베스트팔렌 주에 위치하며 2003년 뒤스부르크 대학교와 에센 대학교의 통합으로 설립되었고, 약 4만 명의 학생이 재학 중이며, 루르 대도시 연합 대학교의 일원으로서 다양한 분야에서 우수한 평가를 받는다.
16세기 도입 - 베를리너 바이세
베를리너 바이세는 16세기 함부르크에서 유래된 신맛이 특징적인 독일 밀맥주 스타일로, 프로이센 왕가 장려와 나폴레옹 군대의 칭송으로 유명해졌으며, 라즈베리나 향기풀 시럽을 첨가하여 제공되기도 하고 독일 외 여러 나라에서 생산된다.
16세기 도입 - 개신교
개신교는 16세기 종교 개혁으로 시작된 기독교의 주요 분파로, 성경의 권위, 믿음을 통한 구원, 만인 제사장설을 강조하며 다양한 교파로 나뉘어 전 세계적으로 9억 명의 신자를 보유하고 비서구 지역에서 빠르게 성장하고 있다.

메르카토르 도법
지도 정보
메르카토르 도법
일반 정보
종류	원통 도법
도법	정각 도법
개발자	제라르두스 메르카토르
발표 연도	1569년
다른 이름	메르카토르 투영법 메르카토르 도법
역사
초기 사용	해상 항법
에르하르트 에츠라우프	1500년대 나침반 지도
제라르두스 메르카토르	1569년 세계지도 제작
특징
장점	각의 정확성 유지 등각도법 해상 항해에 용이 (등각항로가 직선으로 표현됨)
단점	면적 왜곡 (특히 고위도 지역에서 심각) 극지방 표현 불가
수학적 정의
가정	지구는 완전한 구
좌표 변환	x = λ - λ₀ y = ln(tan(π/4 + φ/2)) = atanh(sin φ) = 1/2 ln((1 + sin φ)/(1 - sin φ)) 여기서: λ는 지점의 경도 λ₀는 지도의 중앙 경도 φ는 지점의 위도
역변환	φ = 2 arctan(exp(y)) - π/2 λ = x + λ₀
활용
용도	해상 항법 지도 웹 지도 (구글 지도, 오픈스트리트맵 등)
문제점	면적 왜곡으로 인한 시각적 오해 (국가 크기 비교 등)
기타
관련 도법	갈-피터스 도법 (면적을 보존하는 도법) 밀러 도법 (메르카토르 도법의 수정)

2. 역사

조셉 니덤은 중국 송나라 시대의 일부 항성표가 메르카토르 도법으로 작성되었을 가능성을 추측했으나, 이는 증거 없이 제시되었다.^[1] 천문학 역사가 미야지마 가즈히코는 측량 분석을 통해 이러한 항성표가 정적도법을 사용했다는 결론을 내렸다.^[2]

13세기, 지중해의 가장 오래된 기존 포르톨라노 해도는 의도적인 지도 투영을 기반으로 한 것으로 여겨지지 않지만, 배의 방위를 설정하는 데 사용할 수 있는 교차하는 선의 풍향계 네트워크를 포함하고 있었다. 이 해도는 당시 유럽이나 아랍 학자들이 작성한 지도에서 찾아볼 수 없는 놀라운 정확성을 가지고 있으며, 그 제작 방법은 여전히 수수께끼로 남아 있다.^[3]^[4] 학계의 일반적인 의견과 모순되는 것으로 보이는 측량 분석을 바탕으로, 이 해도는 알려지지 않은 중세 이전의 지도 제작 전통에서 유래했을 가능성이 있으며, 메르카토르 도법에 대한 어떤 고대의 이해를 보여주는 증거일 가능성이 있다는 추측이 제기되었다.^[5]

독일의 폴리매스 에르하르트 에츠라우브는 휴대용 측일기를 조정하기 위해 위도 0°~67°에 걸쳐 유럽과 아프리카 일부 지역의 소형 "나침반 지도"(약 10×8 cm)를 조각했다. 존 스나이더는 1511년에 제작된 이 지도에 사용된 투영이 메르카토르 도법과 같다고 1987년에 언급했다. 그러나, 측일기의 기하학적 구조를 고려할 때, 이 지도는 측일기의 기반이 되는 투영인 직교 원통도법(중심 원통 투영의 극한 경우)과 유사한 투영을 기반으로 했을 가능성이 높다. 스나이더는 1993년에 자신의 평가를 "유사한 투영"으로 수정했다.

포르투갈의 수학자이자 우주지리학자 페드로 누네스는 항해에서 사용할 수 있는, 진북에 대한 일정한 방위를 갖는 경로인 자침 방위선(항정선)의 수학적 원리를 처음으로 설명했다. 그는 1537년에 방향의 왜곡을 최소화하는 방법으로 정적도법으로 여러 개의 대축척 시트로 구성된 항해용 아틀라스를 제작할 것을 제안했다. 이 시트들을 같은 축척으로 만들어 조립하면 메르카토르 도법에 근사하게 된다.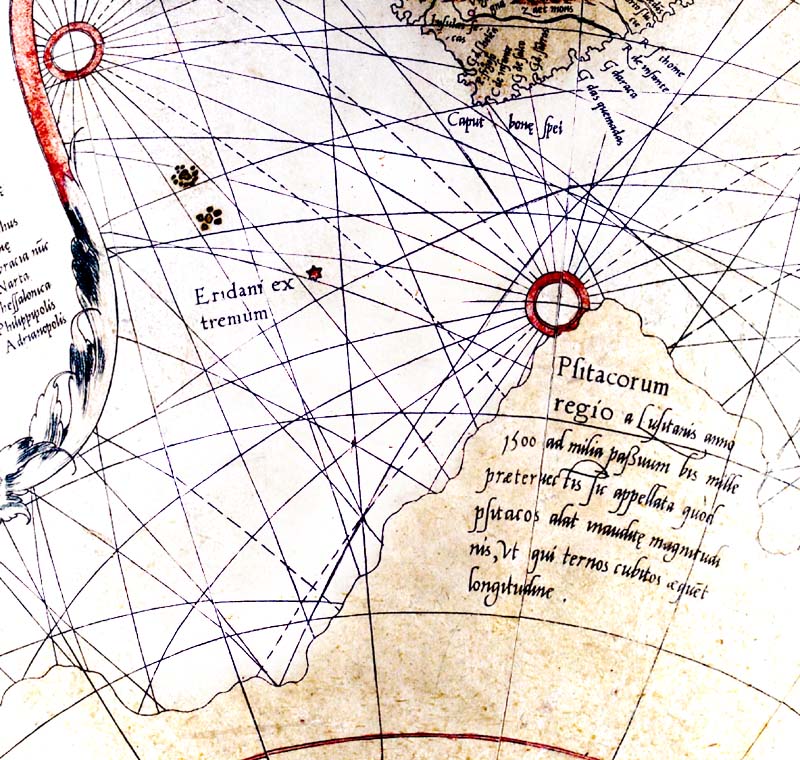

1541년, 플랑드르의 지리학자이자 지도 제작자인 게라르두스 메르카토르는 니콜라 페레노 드 그랑벨을 위해 제작한 지구본에 자침 방위선 네트워크를 포함시켰다.^[6]

1569년, 메르카토르는 202 x 124 cm 크기의 대형 세계 지도를 18개의 별도 시트로 인쇄하여 새로운 투영을 발표했다. 메르카토르는 이 지도의 제목을 Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata^la, "항해사의 사용을 위해 수정된 새롭고 확장된 지구의 묘사"라고 명명했다. 이 제목과 지도의 텍스트 부분에 나타나는 투영 사용에 대한 자세한 설명은 메르카토르가 자신이 무엇을 성취했는지 정확히 이해하고 있으며, 이 투영을 항해에 도움이 되도록 의도했다는 것을 보여준다. 메르카토르는 제작 방법이나 어떻게 도출했는지에 대해서는 설명하지 않았다.^[7] 수년 동안 여러 가설이 제시되었지만, 어떤 경우든 메르카토르와 페드로 누네스의 친분과 누네스가 만든 로크소드롬 표에 접근할 수 있었던 것이 그의 노력에 도움이 되었을 가능성이 높다.^[7]

영국의 수학자 에드워드 라이트는 1599년에, 그리고 1610년에 더 자세하게 이 투영을 구성하기 위한 첫 번째 정확한 표를 발표하여 그의 논문을 "항해의 특정 오류"라고 불렀다. 최초의 수학적 공식은 1645년경 헨리 본드(1600년경~1678년)라는 수학자가 발표했다. 그러나 관련 수학은 1589년경부터 수학자 토머스 해리엇이 개발했지만 발표하지 않았다.

메르카토르 도법의 개발은 16세기 항해 지도 제작에서 중요한 돌파구를 나타냈다. 그러나 당시의 낡은 항해 및 측량 기술과는 호환되지 않았기 때문에 시대를 앞서 나갔다. 그 즉각적인 적용을 막은 두 가지 주요 문제는 바다에서 경도를 충분히 정확하게 결정할 수 없었던 것과 지리적 방향 대신 자기 방향이 항해에 사용되었다는 점이었다. 해상 크로노미터가 발명되고 자기 편각의 공간 분포가 알려진 18세기 중반 이후에야 항해사들이 메르카토르 도법을 완전히 채택할 수 있었다.

이러한 위치 찾기의 한계에도 불구하고, 메르카토르 도법은 메르카토르의 최초 발표 이후 수세기 동안 많은 세계 지도에서 찾아볼 수 있다. 그러나 위치 결정 문제가 대부분 해결된 19세기가 되어서야 세계 지도를 지배하기 시작했다. 메르카토르 도법이 상업 및 교육용 지도의 일반적인 투영이 되자, 육지의 불균형적인 표현과 극지방을 유용하게 표시할 수 없다는 점 때문에 지도 제작자들로부터 지속적인 비판을 받았다.

메르카토르 도법의 부적절한 사용에 대한 비판은 19세기 후반과 20세기 초에 많은 새로운 발명을 촉진했으며, 종종 메르카토르 도법의 대안으로 직접 홍보되었다. 이러한 압력으로 인해 출판사들은 20세기 동안 투영의 사용을 점차 줄였다. 그러나 웹 매핑의 출현은 웹 메르카토르 도법의 형태로 투영의 급격한 부활을 가져왔다.

오늘날 메르카토르 도법은 해도, 가끔 세계 지도, 웹 매핑 서비스에서 찾아볼 수 있지만, 상업용 아틀라스에서는 대부분 사라졌고, 세계 벽걸이 지도는 많은 대체 투영으로 찾아볼 수 있다. 2005년부터 이를 사용해 온 구글 지도는 여전히 지역 지도에 이를 사용하지만, 2017년 데스크톱 플랫폼에서 지역을 확대하지 않은 지도에 대한 투영을 삭제했다. 다른 많은 온라인 매핑 서비스는 여전히 웹 메르카토르 도법을 독점적으로 사용하고 있다.

메르카토르는 직선을 그음으로써 등각 항로를 구할 수 있는 지도를 만들고자 했던 것 같다.^[27] 그러나 메르카토르 시대에는 아직 적분법이 알려져 있지 않았고, 적도에서 각 위도까지의 지도상 거리를 나타내는 정적분

:

u = \int_0^\varphi\sec\theta{\rm d}\theta = \ln\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) = \tanh^{-1} \sin\varphi = \operatorname{gd}^{-1}\varphi

을 메르카토르는 급수로 근사적으로 계산하는 데 그쳤으며, 작도에 필요한 수학적 근거를 명확히 밝히지 않았기 때문에 메르카토르 도법은 보급되지 않았다.

해도를 비롯한 세계 지도에 사용되기 시작한 것은 1599년에 영국의 에드워드 라이트가 수치 계산법(오늘날의 리만 합에 의한 방법)을 이용하여 위선 거리를 유도하고 작도에 필요한 수표를 작성한 이후부터이다. 이 정적분을 구하는 문제는 17세기 중기에 지도학을 목적으로 하는 수학적 관심사로서 거론되었지만(정현 함수의 적분/Integral of the secant function^영어 문제^[28]), 해당 적분은 아이작 배로에 의해 처음으로 닫힌 식/Closed-form expression^영어으로 구해졌다고 알려져 있으며(연대 불명), 1668년에 제임스 그레고리에 의해서도 구해졌다. 오늘날에는 이 위선 거리

u

의 식은 상술한 람베르트 함수(역 구델만 함수)

\operatorname{gd}^{-1}\varphi

에 해당한다고 해석된다.

2. 1. 초기 역사

조셉 니덤은 중국 송나라 시대의 일부 항성표가 메르카토르 도법으로 작성되었을 가능성을 추측했으나, 이는 증거 없이 제시되었다.^[1] 천문학 역사가 미야지마 가즈히코는 측량 분석을 통해 이러한 항성표가 정적도법을 사용했다는 결론을 내렸다.^[2]

13세기, 지중해의 가장 오래된 기존 포르톨라노 해도는 의도적인 지도 투영을 기반으로 한 것으로 여겨지지 않지만, 배의 방위를 설정하는 데 사용할 수 있는 교차하는 선의 풍향계 네트워크를 포함하고 있었다. 이 해도는 당시 유럽이나 아랍 학자들이 작성한 지도에서 찾아볼 수 없는 놀라운 정확성을 가지고 있으며, 그 제작 방법은 여전히 수수께끼로 남아 있다.^[3]^[4] 학계의 일반적인 의견과 모순되는 것으로 보이는 측량 분석을 바탕으로, 이 해도는 알려지지 않은 중세 이전의 지도 제작 전통에서 유래했을 가능성이 있으며, 메르카토르 도법에 대한 어떤 고대의 이해를 보여주는 증거일 가능성이 있다는 추측이 제기되었다.^[5]

독일의 폴리매스 에르하르트 에츠라우브는 휴대용 측일기를 조정하기 위해 위도 0°~67°에 걸쳐 유럽과 아프리카 일부 지역의 소형 "나침반 지도"(약 10×8 cm)를 조각했다. 존 스나이더는 1511년에 제작된 이 지도에 사용된 투영이 메르카토르 도법과 같다고 1987년에 언급했다. 그러나, 측일기의 기하학적 구조를 고려할 때, 이 지도는 측일기의 기반이 되는 투영인 직교 원통도법(중심 원통 투영의 극한 경우)과 유사한 투영을 기반으로 했을 가능성이 높다. 스나이더는 1993년에 자신의 평가를 "유사한 투영"으로 수정했다.

포르투갈의 수학자이자 우주지리학자 페드로 누네스는 항해에서 사용할 수 있는, 진북에 대한 일정한 방위를 갖는 경로인 자침 방위선(항정선)의 수학적 원리를 처음으로 설명했다. 그는 1537년에 방향의 왜곡을 최소화하는 방법으로 정적도법으로 여러 개의 대축척 시트로 구성된 항해용 아틀라스를 제작할 것을 제안했다. 이 시트들을 같은 축척으로 만들어 조립하면 메르카토르 도법에 근사하게 된다.

1541년, 플랑드르의 지리학자이자 지도 제작자인 게라르두스 메르카토르는 니콜라 페레노 드 그랑벨을 위해 제작한 지구본에 자침 방위선 네트워크를 포함시켰다.^[6]

1569년, 메르카토르는 202 x 124 cm 크기의 대형 세계 지도를 18개의 별도 시트로 인쇄하여 새로운 투영을 발표했다. 메르카토르는 이 지도의 제목을 Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata^la, "항해사의 사용을 위해 수정된 새롭고 확장된 지구의 묘사"라고 명명했다. 이 제목과 지도의 텍스트 부분에 나타나는 투영 사용에 대한 자세한 설명은 메르카토르가 자신이 무엇을 성취했는지 정확히 이해하고 있으며, 이 투영을 항해에 도움이 되도록 의도했다는 것을 보여준다. 메르카토르는 제작 방법이나 어떻게 도출했는지에 대해서는 설명하지 않았다.^[7] 수년 동안 여러 가설이 제시되었지만, 어떤 경우든 메르카토르와 페드로 누네스의 친분과 누네스가 만든 로크소드롬 표에 접근할 수 있었던 것이 그의 노력에 도움이 되었을 가능성이 높다.^[7]

영국의 수학자 에드워드 라이트는 1599년에, 그리고 1610년에 더 자세하게 이 투영을 구성하기 위한 첫 번째 정확한 표를 발표하여 그의 논문을 "항해의 특정 오류"라고 불렀다. 최초의 수학적 공식은 1645년경 헨리 본드(1600년경~1678년)라는 수학자가 발표했다. 그러나 관련 수학은 1589년경부터 수학자 토머스 해리엇이 개발했지만 발표하지 않았다.

메르카토르 도법의 개발은 16세기 항해 지도 제작에서 중요한 돌파구를 나타냈다. 그러나 당시의 낡은 항해 및 측량 기술과는 호환되지 않았기 때문에 시대를 앞서 나갔다. 그 즉각적인 적용을 막은 두 가지 주요 문제는 바다에서 경도를 충분히 정확하게 결정할 수 없었던 것과 지리적 방향 대신 자기 방향이 항해에 사용되었다는 점이었다. 해상 크로노미터가 발명되고 자기 편각의 공간 분포가 알려진 18세기 중반 이후에야 항해사들이 메르카토르 도법을 완전히 채택할 수 있었다.

이러한 위치 찾기의 한계에도 불구하고, 메르카토르 도법은 메르카토르의 최초 발표 이후 수세기 동안 많은 세계 지도에서 찾아볼 수 있다. 그러나 위치 결정 문제가 대부분 해결된 19세기가 되어서야 세계 지도를 지배하기 시작했다. 메르카토르 도법이 상업 및 교육용 지도의 일반적인 투영이 되자, 육지의 불균형적인 표현과 극지방을 유용하게 표시할 수 없다는 점 때문에 지도 제작자들로부터 지속적인 비판을 받았다.

메르카토르 도법의 부적절한 사용에 대한 비판은 19세기 후반과 20세기 초에 많은 새로운 발명을 촉진했으며, 종종 메르카토르 도법의 대안으로 직접 홍보되었다. 이러한 압력으로 인해 출판사들은 20세기 동안 투영의 사용을 점차 줄였다. 그러나 웹 매핑의 출현은 웹 메르카토르 도법의 형태로 투영의 급격한 부활을 가져왔다.

오늘날 메르카토르 도법은 해도, 가끔 세계 지도, 웹 매핑 서비스에서 찾아볼 수 있지만, 상업용 아틀라스에서는 대부분 사라졌고, 세계 벽걸이 지도는 많은 대체 투영으로 찾아볼 수 있다. 2005년부터 이를 사용해 온 구글 지도는 여전히 지역 지도에 이를 사용하지만, 2017년 데스크톱 플랫폼에서 지역을 확대하지 않은 지도에 대한 투영을 삭제했다. 다른 많은 온라인 매핑 서비스는 여전히 웹 메르카토르 도법을 독점적으로 사용하고 있다.

메르카토르는 직선을 그음으로써 등각 항로를 구할 수 있는 지도를 만들고자 했던 것 같다.^[27] 그러나 메르카토르 시대에는 아직 적분법이 알려져 있지 않았고, 적도에서 각 위도까지의 지도상 거리를 나타내는 정적분

:

u = \int_0^\varphi\sec\theta{\rm d}\theta = \ln\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) = \tanh^{-1} \sin\varphi = \operatorname{gd}^{-1}\varphi

을 메르카토르는 급수로 근사적으로 계산하는 데 그쳤으며, 작도에 필요한 수학적 근거를 명확히 밝히지 않았기 때문에 메르카토르 도법은 보급되지 않았다.

해도를 비롯한 세계 지도에 사용되기 시작한 것은 1599년에 영국의 에드워드 라이트가 수치 계산법(오늘날의 리만 합에 의한 방법)을 이용하여 위선 거리를 유도하고 작도에 필요한 수표를 작성한 이후부터이다. 이 정적분을 구하는 문제는 17세기 중기에 지도학을 목적으로 하는 수학적 관심사로서 거론되었지만(정현 함수의 적분/Integral of the secant function^영어 문제^[28]), 해당 적분은 아이작 배로에 의해 처음으로 닫힌 식/Closed-form expression^영어으로 구해졌다고 알려져 있으며(연대 불명), 1668년에 제임스 그레고리에 의해서도 구해졌다. 오늘날에는 이 위선 거리

u

의 식은 상술한 람베르트 함수(역 구델만 함수)

\operatorname{gd}^{-1}\varphi

에 해당한다고 해석된다.

2. 2. 메르카토르의 발표 (1569년)

1569년, 플랑드르의 지리학자이자 지도 제작자인 메르카토르는 크기의 대형 세계 지도를 18개의 별도 시트로 인쇄하여 새로운 투영법을 발표했다.^[7] 메르카토르는 이 지도의 제목을 Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata^la로, "항해사의 사용을 위해 수정된 새롭고 확장된 지구의 묘사"라고 명명했다.^[7] 이 제목과 지도의 텍스트 부분에 나타나는 투영 사용에 대한 자세한 설명은 메르카토르가 자신이 무엇을 성취했는지 정확히 이해하고 있으며, 이 투영을 항해에 도움이 되도록 의도했다는 것을 보여준다.^[7]

메르카토르는 등각 항로를 직선으로 표현할 수 있는 지도를 만들고자 했다.^[27] 그러나 그는 제작 방법이나 도출 과정을 명확히 설명하지 않았다.^[7] 수년 동안 여러 가설이 제시되었지만, 메르카토르가 페드로 누네스와 친분이 있었고 누네스가 만든 로크소드롬 표에 접근할 수 있었다는 점이 그의 노력에 도움이 되었을 가능성이 높다.^[7] 당시에는 적분법이 알려지지 않았기 때문에, 메르카토르는 적도에서 각 위도까지의 지도상 거리를 나타내는 정적분을 급수를 통해 근사적으로 계산하는 데 그쳤다.^[28]

메르카토르 도법이 해도와 세계 지도에 사용되기 시작한 것은 1599년 영국의 가 수치 계산법(오늘날의 리만 합에 의한 방법)을 이용하여 위선 거리를 유도하고 작도에 필요한 수표를 작성한 이후부터이다.^[28]

1541년, 메르카토르는 니콜라 페레노 드 그랑벨(Nicolas Perrenot de Granvelle)을 위해 제작한 지구본에 자침 방위선 네트워크를 포함시킨 적이 있었다.^[6]

한편, 조셉 니덤(Joseph Needham)은 중국 송나라 시대의 일부 항성표가 메르카토르 도법으로 작성되었을 가능성을 추측했으나, 이는 증거 없이 제시된 주장이다.^[1] 천문학 역사가 미야지마 가즈히코(Kazuhiko Miyajima)는 측량 분석을 통해 이러한 항성표가 정적도법을 사용했다는 결론을 내렸다.^[2]

13세기 지중해의 포르톨라노 해도는 교차하는 선의 풍향계 네트워크를 포함하고 있었는데, 이는 알려지지 않은 중세 이전의 지도 제작 전통에서 유래했을 가능성이 있으며, 메르카토르 도법에 대한 어떤 고대의 이해를 보여주는 증거일 수 있다는 추측이 제기되었다.^[5]

독일의 에르하르트 에츠라우브(Erhard Etzlaub)는 1511년에 위도 0°~67°에 걸쳐 유럽과 아프리카 일부 지역의 소형 "나침반 지도"를 조각했는데, 존 스나이더(John P. Snyder)는 이 지도에 사용된 투영이 메르카토르의 투영과 같다고 언급했다.^[3]

포르투갈의 페드로 누네스(Pedro Nunes)는 1537년에 진북에 대한 일정한 방위를 갖는 경로인 자침 방위선(로크소드롬)의 수학적 원리를 처음으로 설명하고, 정적도법으로 여러 개의 대축척 시트로 구성된 항해용 아틀라스를 제작할 것을 제안했다. 이 시트들을 같은 축척으로 만들어 조립하면 메르카토르 도법에 근사하게 된다.

2. 3. 수학적 발전

메르카투스는 직선을 그어 등각 항로를 구할 수 있는 지도를 만들고자 했다.^[27] 그러나 메르카투스 시대에는 아직 적분법이 알려져 있지 않았고, 적도에서 각 위도까지의 지도상 거리를 나타내는 정적분

:

u = \int_0^\varphi\sec\theta{\rm d}\theta = \ln\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) = \tanh^{-1} \sin\varphi = \operatorname{gd}^{-1}\varphi

을 급수로 근사적으로 계산하는 데 그쳤으며, 작도에 필요한 수학적 근거를 명확히 밝히지 않았기 때문에 메르카투스 도법은 보급되지 않았다.

해도를 비롯한 세계 지도에 사용되기 시작한 것은 1599년에 영국의 에드워드 라이트가 수치 계산법(오늘날의 리만 합에 의한 방법)을 이용하여 위선 거리를 유도하고 작도에 필요한 수표를 작성한 이후부터이다. 이 정적분을 구하는 문제는 17세기 중기에 지도학을 목적으로 하는 수학적 관심사로서 거론되었지만(Integral of the secant function^영어 문제^[28]), 해당 적분은 아이작 배로에 의해 처음으로 닫힌 식(Closed-form expression^영어)으로 구해졌다고 알려져 있으며(연대 불명), 1668년에 제임스 그레고리에 의해서도 구해졌다. 오늘날에는 이 위선 거리

u

의 식은 상술한 람베르트 함수(역 구델만 함수)

\operatorname{gd}^{-1}\varphi

에 해당한다고 해석된다.

2. 4. 확산과 비판

메르카토르 도법은 지도상의 육지 면적 왜곡으로 인해 비판을 받았다. 조지 켈러웨이(George Kellaway)와 어빙 피셔(Irving Fisher) 등은 이 투영법이 일반적인 세계 지도에 부적합하다고 평가했다.^[11] 특히 적도 부근 국가들이 유럽과 북미 국가들에 비해 지나치게 작게 표시되어, 이들 국가를 덜 중요하게 여기도록 만든다는 비판도 있었다.^[11] 메르카토르 자신은 이러한 문제를 인식하여 등적도법인 사인곡선 투영법을 사용하여 상대적인 면적을 나타내기도 했다.

이러한 비판에도 불구하고, 메르카토르 투영법은 19세기 후반과 20세기 초에 세계 지도에 가장 흔하게 사용되었다.^[12]^[13]^[14] 그러나 1940년대부터 많은 지도첩에서 메르카토르 투영법 대신 다른 원통도법이나 등적 투영법을 사용하기 시작했다. 다만, 적도 부근 지역에서는 왜곡이 적어 여전히 자주 사용되며, 시간대 지도에도 활용된다.

아르노 페터스(Arno Peters)는 1972년 메르카토르 투영법의 문제점을 해결하기 위해 갈-페터스 투영법을 제안하며 논쟁을 일으켰다. 그는 자신의 투영법이 독창적인 것이라고 주장했지만, 실제로는 원통 등적 투영법의 특정 매개변수화였다. 1989년 북미의 7개 지리학 단체는 메르카토르 투영법과 갈-페터스 투영법을 포함한 일반적인 세계 지도에 원통 투영법 사용을 반대하는 결의안을 채택했다.^[15]

메르카토르는 등각 항로를 직선으로 표현할 수 있는 지도를 만들고자 했다.^[27] 하지만 당시에는 적분법이 알려지지 않아, 위선 거리를 급수로 근사 계산하여 명확한 수학적 근거를 제시하지 못했다. 1599년 영국의 에드워드 라이트가 수치 해석을 통해 위선 거리를 유도하고 수표를 작성한 이후 해도 제작 등에 사용되기 시작했다. 위선 거리를 구하는 문제는 17세기 중기에 지도학의 중요한 문제로 떠올랐으며( 문제^[28]), 아이작 배로와 제임스 그레고리가 이를 해결했다.

2. 5. 현대의 사용

메르카토르는 직선을 그어 등각 항로를 구할 수 있는 지도를 만들고자 했다.^[27] 그러나 당시에는 적분법이 알려지지 않아, 적도에서 각 위도까지의 지도상 거리를 나타내는 정적분을 급수로 근사 계산하여 작도에 필요한 수학적 근거를 명확히 밝히지 못했다. 이 때문에 메르카토르 도법은 널리 보급되지 않았다.

1599년 영국의 에드워드 라이트가 수치 계산법(오늘날의 리만 합)을 이용하여 위선 거리를 유도하고 작도에 필요한 수표를 작성한 이후부터 해도와 세계 지도에 사용되기 시작했다. 이 정적분을 구하는 문제는 17세기 중기에 지도학을 위한 수학적 관심사로 거론되었으며( 문제^[28]), 아이작 배로가 처음으로 닫힌 식으로 구했다고 알려져 있다(연대 불명). 1668년에는 제임스 그레고리도 같은 결과를 얻었다. 오늘날 이 위선 거리의 식은 람베르트 함수(역 구델만 함수)에 해당한다고 해석된다.

3. 특징

메르카토르 도법은 원통을 구에 꼭 맞게 감싼 형태로 시각화할 수 있으며, 등각성을 유지하여 구면 표면을 원통으로 펼친 후 평면에 펼쳐 지도를 만든다.^[8] 이 과정에서 축척은 접촉 원(일반적으로 적도)을 따라 정확하게 유지되지만, 접촉원에서 멀어질수록 비선형적으로 증가한다.^[8] 표준 평행선을 설정하여 특정 영역의 축척을 조정할 수 있지만, 이는 구와 할선 원통에 대한 투영으로 오해될 수 있다.^[8]

정규 양상의 메르카토르 도법에서 위도선과 경도선은 직선으로 나타나며 서로 수직으로 교차한다.^[8] 지구상의 위도선은 극에 가까워질수록 작아지지만, 모든 원통형 지도 투영에서 길이가 균일하도록 동서 방향으로 늘어난다.^[8] 메르카토르 도법은 이러한 동서 방향 늘어짐을 남북 방향 늘어짐과 균형을 이루도록 하여, 모든 위치에서 축척이 국지적으로 균일하고 각도가 보존된다. ^[8]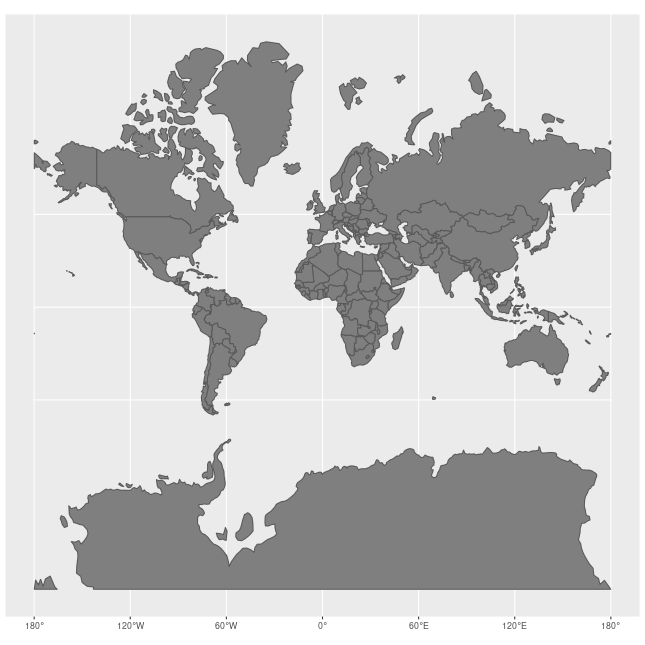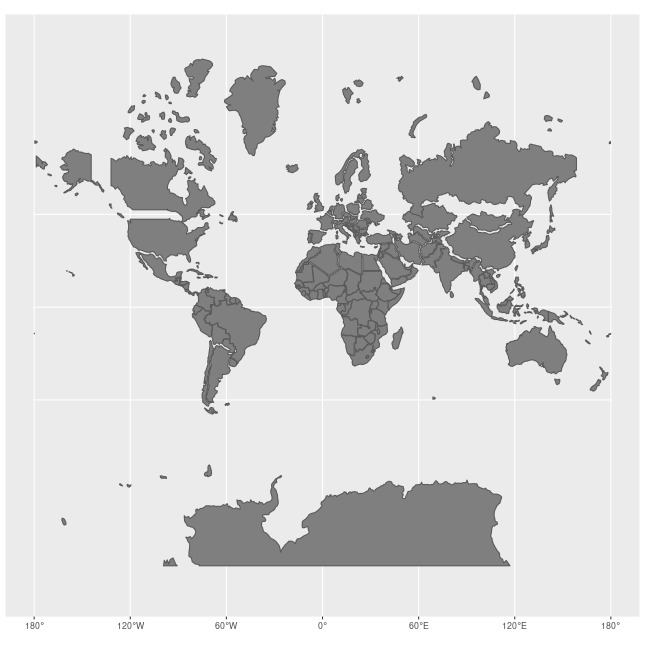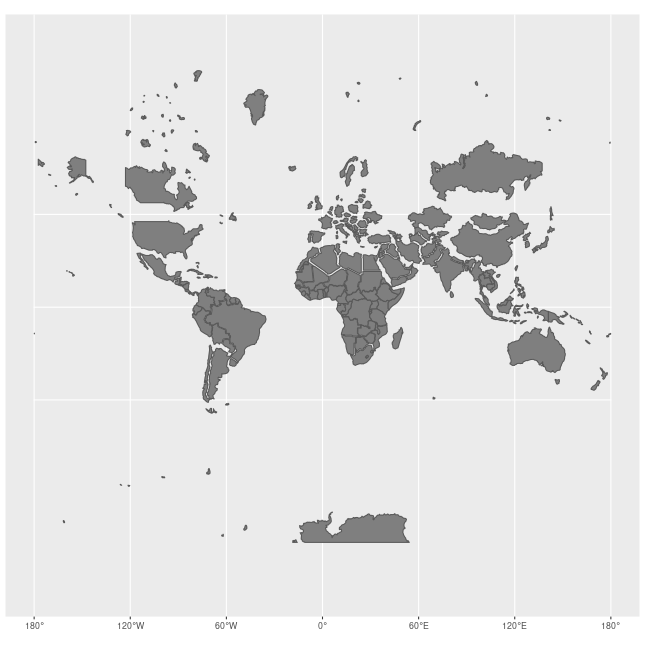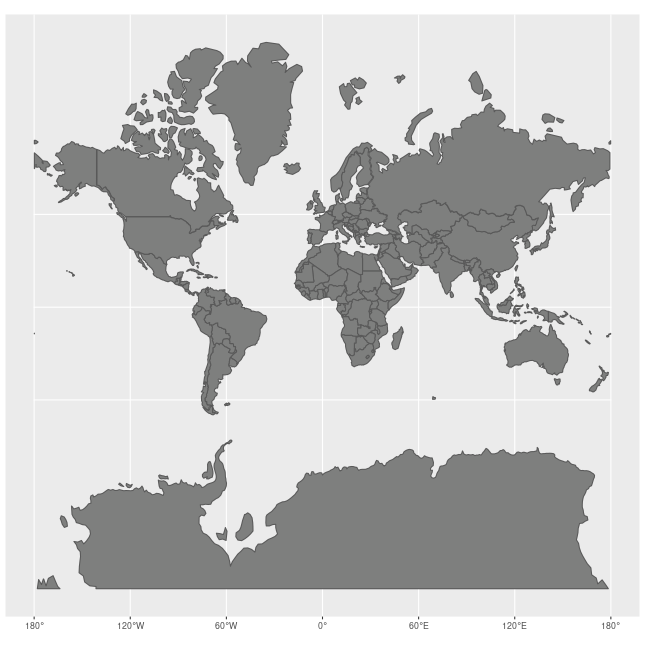

축척 비교: 정규, 사투, 가로 메르카토르 도법의 접선 및 할선 형태, 표준 평행선은 빨간색

왜곡된 크기와 실제 크기의 비율. 지도가 정치적 경계선을 따라 여러 번 중단됨에 유의

360° 원통도법: 정적도법, 밀러 도법, 메르카토르 도법 및 진정한 원통도법.

빨간 원(티소의 지시 타원)은 지구상의 같은 크기의 원을 메르카토르 도법으로 투영한 것이다. 어떤 원도 작으면 왜곡 없이 원이 되지만, 크기는 위도에 따라 다르다

메르카토르 도법은 등각항로(일정 방위)를 지도의 직선으로 표현하여 해상 항해에 적합하다.^[8] 나침반 장미나 각도기로 진로와 방위를 측정하고, 평행자를 사용하여 지도상의 위치를 쉽게 전달할 수 있다.^[8]

그러나 선형 축척은 위도에 따라 증가하여 적도에서 멀리 떨어진 지역의 크기를 왜곡하고, 특히 극지방에서는 무한대로 커져 사용할 수 없다.^[8] 예를 들어, 그린란드는 아프리카와 비슷한 크기로 보이지만 실제로는 아프리카가 14배 더 크다.^[10] 알래스카는 브라질과 비슷하게 보이지만 브라질이 거의 5배 더 크다. 마다가스카르는 그레이트브리튼과 비슷해 보이지만 마다가스카르가 두 배 이상 크다.

메르카토르 도법은 출발지와 목적지 사이의 직선을 그어 경선과 이루는 각도를 재고, 나침반을 보면서 항상 그 각도로 나아가면 목적지에 도착하는 항정선(등각항로)개념을 사용한다. 이는 경선이 평행직선이며, 정각도법이기 때문이다.

메르카토르 도법의 가장 큰 특징은 각도가 정확하다는 것이지만, 위도에 따라 축척이 변하고 고위도 지방은 크게 확대된다. 따라서 넓은 범위에서 각도, 거리, 면적비는 정확하지 않다. 극에서는 가로와 세로 방향 모두 무한대로 확대되어 표현할 수 없다. 밀러 도법은 이러한 왜곡을 줄이기 위해 경선 방향의 늘어남을 압축했지만, 정각성을 잃었다.

최근 인터넷에서 시임리스한 세계 지도를 표현하는 방법으로 사용되고 있으며, 북쪽이 항상 위이고 정각도법이므로 충분히 확대하면 왜곡이 문제가 되지 않는다. 그러나 축척은 위도에 따라 변하므로 비교를 위한 눈금을 변경해야 한다.^[25]

4. 수학적 특성

구를 기준으로 할 때 위도 φ인 지역은 sec(φ)배 확대해야 정각성을 유지하게 된다. 따라서 반지름 R, 중앙 경선을 λ₀으로 둘 때 경도 λ, 위도 φ인 지점은 메르카토르 도법에서 아래와 같은 위치로 옮겨진다.^[22]^[23]

:

\begin{align}x &= R( \lambda - \lambda_0), \qquad \\y &= R\log \left[\tan \left(\frac{\pi}{4} + \frac{\phi}{2} \right) \right].\end{align}

함수 y(φ)는 R = 1인 경우 φ와 함께 그려지는데, 극점에서 무한대로 발산한다. 선형 y축 값은 인쇄된 지도에 일반적으로 표시되지 않고, 대신 일부 지도는 오른쪽에 비선형 위도 값 눈금을 표시한다. 대부분의 지도는 선택된 자오선과 평행선의 격자만 표시한다.

y(φ)에 대한 여러 가지 다른 표현식은 다음과 같으며, 모두 기본적인 변환을 통해 유도된 것이다.^[23]

:

\begin{align}y & = &  \frac {R}{2} \ln \left[ \frac {1 + \sin\varphi}{1 - \sin\varphi} \right]& = &  {R} \ln \left[ \frac {1 + \sin\varphi}{\cos\varphi} \right]& =    R\ln \left(\sec\varphi + \tan\varphi\right) \\[2ex]& = &  R\tanh^{-1}\left(\sin\varphi\right)& = &  R\sinh^{-1}\left(\tan\varphi\right)& =    R\operatorname{sgn}(\varphi)\cosh^{-1}\left(\sec\varphi\right)=    R\operatorname{gd}^{-1}(\varphi) .\end{align}

이에 대응하는 역변환은 다음과 같다.

:

\varphi = \sin^{-1}\left(\tanh\frac{y}{R}\right)= \tan^{-1}\left(\sinh\frac{y}{R}\right)= \operatorname{sgn}(y)\sec^{-1}\left(\cosh\frac{y}{R}\right)= \operatorname{gd}\frac{y}{R}.

각도를 도(degree) 단위로 표현하면 다음과 같다.

:

x = \frac{\pi R(\lambda^\circ-\lambda^\circ_0)}{180}, \qquad\quady = R\ln \left[\tan \left(45 + \frac{\varphi^\circ}{2} \right) \right].

위 공식은 지구 반지름 R을 기준으로 작성되었으며, 지도 너비 W = 2πR을 직접 사용하는 것이 편리한 경우가 많다. 예를 들어, 기본 변환 방정식은 다음과 같이 된다.

:

x = \frac{W}{2\pi}\left( \lambda - \lambda_0\right), \qquad\quady = \frac{W}{2\pi}\ln \left[\tan \left(\frac{\pi}{4} + \frac{\varphi}{2} \right) \right].

지도의 중앙 경도가

\lambda_0

일 때, 반지름을 1로 하는 단위구면에서 지리좌표

\lambda,\,\varphi

의 점이 투영되는 메르카토르 도법 지도상의 점

x,\,y

는 다음과 같다.

:

\begin{align}x & = \lambda - \lambda_0 \\y & = \ln\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) \\& = \tanh^{-1} \sin\varphi \\& = \operatorname{gd}^{-1}\varphi \\\end{align}

구델만 함수의 역함수

\operatorname{gd}^{-1}\varphi

는 람베르트 함수라고도 불린다.

회전타원체 모델에서,

y

좌표를 축소할 필요가 있으며, 장반축을 1, 제1이심률을

e

로 하면,

:

\begin{align}y = \tanh^{-1} \sin\varphi - e \tanh^{-1}(e\sin\varphi)\end{align}

가 된다. 이 값을 새로운 위도로 간주할 수 있으며, 그 경우 이 값은 “등장위도”라고 불린다.

구글 지도에서는

y

좌표의 투영식에서

e=0

으로 두고 있으므로 정확한 정각투영이 되지 않는다.^[26]

4. 1. 공식

구를 기준으로 할 때 위도 φ인 지역은 sec(φ)배 확대해야 정각성을 유지하게 된다. 따라서 반지름 R, 중앙 경선을 λ₀으로 둘 때 경도 λ, 위도 φ인 지점은 메르카토르 도법에서 아래와 같은 위치로 옮겨진다.^[22]^[23]

:

\begin{align}x &= R( \lambda - \lambda_0), \qquad \\y &= R\log \left[\tan \left(\frac{\pi}{4} + \frac{\phi}{2} \right) \right].\end{align}

함수 y(φ)는 R = 1인 경우 φ와 함께 그려지는데, 극점에서 무한대로 발산한다. 선형 y축 값은 인쇄된 지도에 일반적으로 표시되지 않고, 대신 일부 지도는 오른쪽에 비선형 위도 값 눈금을 표시한다. 대부분의 지도는 선택된 자오선과 평행선의 격자만 표시한다.

y(φ)에 대한 여러 가지 다른 표현식은 다음과 같으며, 모두 기본적인 변환을 통해 유도된 것이다.^[23]

:

\begin{align}y & = &  \frac {R}{2} \ln \left[ \frac {1 + \sin\varphi}{1 - \sin\varphi} \right]& = &  {R} \ln \left[ \frac {1 + \sin\varphi}{\cos\varphi} \right]& =    R\ln \left(\sec\varphi + \tan\varphi\right) \\[2ex]& = &  R\tanh^{-1}\left(\sin\varphi\right)& = &  R\sinh^{-1}\left(\tan\varphi\right)& =    R\operatorname{sgn}(\varphi)\cosh^{-1}\left(\sec\varphi\right)=    R\operatorname{gd}^{-1}(\varphi) .\end{align}

이에 대응하는 역변환은 다음과 같다.

:

\varphi = \sin^{-1}\left(\tanh\frac{y}{R}\right)= \tan^{-1}\left(\sinh\frac{y}{R}\right)= \operatorname{sgn}(y)\sec^{-1}\left(\cosh\frac{y}{R}\right)= \operatorname{gd}\frac{y}{R}.

각도를 도(degree) 단위로 표현하면 다음과 같다.

:

x = \frac{\pi R(\lambda^\circ-\lambda^\circ_0)}{180}, \qquad\quady = R\ln \left[\tan \left(45 + \frac{\varphi^\circ}{2} \right) \right].

위 공식은 지구 반지름 R을 기준으로 작성되었으며, 지도 너비 W = 2πR을 직접 사용하는 것이 편리한 경우가 많다. 예를 들어, 기본 변환 방정식은 다음과 같이 된다.

:

x = \frac{W}{2\pi}\left( \lambda - \lambda_0\right), \qquad\quady = \frac{W}{2\pi}\ln \left[\tan \left(\frac{\pi}{4} + \frac{\varphi}{2} \right) \right].

지도의 중앙 경도가

\lambda_0

일 때, 반지름을 1로 하는 단위구면에서 지리좌표

\lambda,\,\varphi

의 점이 투영되는 메르카토르 도법 지도상의 점

x,\,y

는 다음과 같다.

:

\begin{align}x & = \lambda - \lambda_0 \\y & = \ln\tan\left(\frac{\pi}{4} + \frac{\varphi}{2}\right) \\& = \tanh^{-1} \sin\varphi \\& = \operatorname{gd}^{-1}\varphi \\\end{align}

구델만 함수의 역함수

\operatorname{gd}^{-1}\varphi

는 람베르트 함수라고도 불린다.

회전타원체 모델에서,

y

좌표를 축소할 필요가 있으며, 장반축을 1, 제1이심률을

e

로 하면,

:

\begin{align}y = \tanh^{-1} \sin\varphi - e \tanh^{-1}(e\sin\varphi)\end{align}

가 된다. 이 값을 새로운 위도로 간주할 수 있으며, 그 경우 이 값은 “등장위도”라고 불린다.

구글 지도에서는

y

좌표의 투영식에서

e=0

으로 두고 있으므로 정확한 정각투영이 되지 않는다.^[26]

4. 2. 역변환

메르카토르 도법의 역변환 방정식은 다음과 같다.^[22]

:

\lambda = \lambda_0 + \frac{x}{R}, \qquad\varphi = 2\tan^{-1}\left[\exp\left(\frac{y}{R}\right)\right] - \frac{\pi}{2} \,.

여기서 λ는 경도, φ는 위도, R은 지구 반지름, λ₀는 기준 경도, x와 y는 각각 가로축과 세로축 좌표이다.

두 번째 방정식의 우변은 구데르만 함수를 정의한다. 즉, φ = gd(y/R)이다. 따라서 직접 방정식은 y = R·gd⁻¹(φ)로 쓸 수 있다.^[22]

4. 3. 절사

메르카토르 도법은 대개 남북위 85° 가량에서 절사하여 사용하는데, 이는 양 극으로 갈수록 지도상의 거리가 무한대로 발산하여 유한한 공간 안에 모두 담을 수 없기 때문이다. 종횡비가 1:1이 되게 하는 값이 약 85°이다.

원통도법에서 가로 길이는 지구 둘레와 같은 2πR이다. 종횡비가 1:1이 되려면 y = -πR부터 y = πR까지 절단하면 되므로, 역변환 식에 y = πR을 대입하면 φ = arcsin(tanh(π)) ≈ 1.484422가 된다. 이를 육십분법으로 환산하면 약 85° 3' 4''가 된다.

메르카토르 도법에서 세로축 y는 극점에서 무한대가 되므로, 지도는 90°보다 작은 위도에서 잘라내야 한다. 메르카토르의 원본 지도는 북위 80°와 남위 66°에서 잘려 있으며, 그 결과 유럽 국가들이 지도 중앙으로 이동되었다. 많은 웹 기반 매핑은 종횡비가 1인 메르카토르 도법의 확대/축소 가능한 버전을 사용한다. 이 경우 도달할 수 있는 최대 위도는 다음과 같이 계산할 수 있다.

:

\varphi = \tan^{-1}\left[\sinh\left(\frac{y}{R}\right)\right]= \tan^{-1}\left[\sinh\pi\right]= \tan^{-1}\left[11.5487\right]= 85.05113^\circ.

4. 4. 축척

메르카토르 투영은 등각 투영이다. 그 결과로 "척도계수의 등방성"이 나타나는데, 이는 점 척도계수가 방향과 무관하다는 것을 의미하며, 작은 모양이 투영에 의해 보존된다는 것을 뜻한다. 수직 척도계수 ''h''는 수평 척도계수 ''k''와 같으며, ''k'' = sec ''φ''이므로 ''h''도 같다.

위도에 따른 척도계수의 변화는 다음과 같다.

위도 30°에서 척도계수는 ''k'' = sec 30° = 1.15
위도 45°에서 척도계수는 ''k'' = sec 45° = 1.41
위도 60°에서 척도계수는 ''k'' = sec 60° = 2
위도 80°에서 척도계수는 ''k'' = sec 80° = 5.76
위도 85°에서 척도계수는 ''k'' = sec 85° = 11.5

면적 척도계수는 평행선과 자오선 척도의 곱으로 ''hk'' = sec²''φ''이다. 그린란드의 경우, 중간 위도를 73°로 하면 ''hk'' = 11.7이다. 오스트레일리아는 중간 위도를 25°로 하면 ''hk'' = 1.2이고, 영국은 중간 위도를 55°로 하면 ''hk'' = 3.04이다.

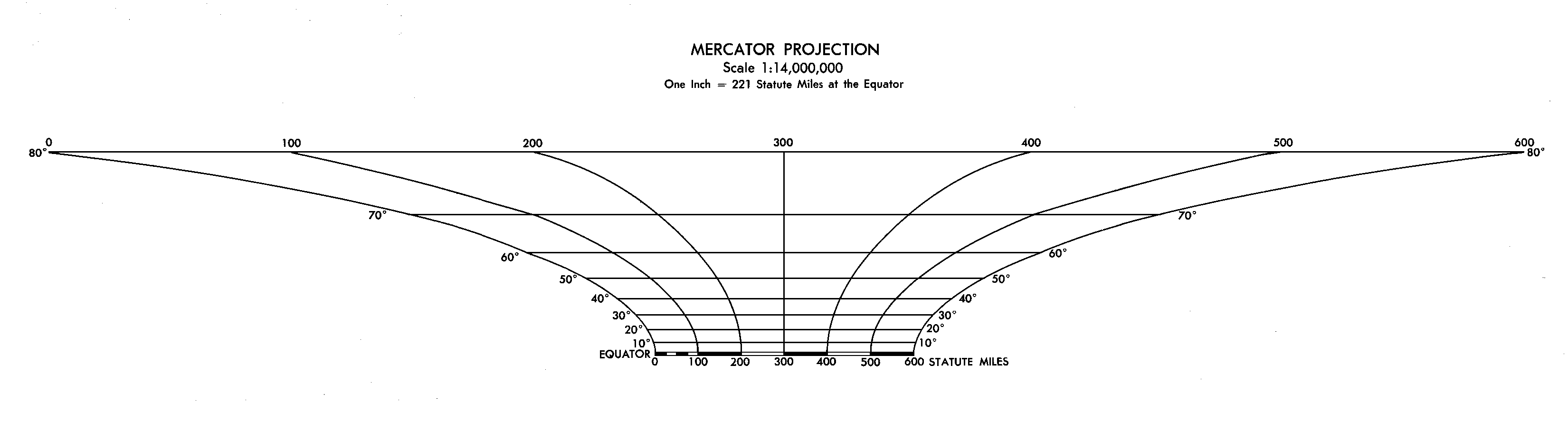
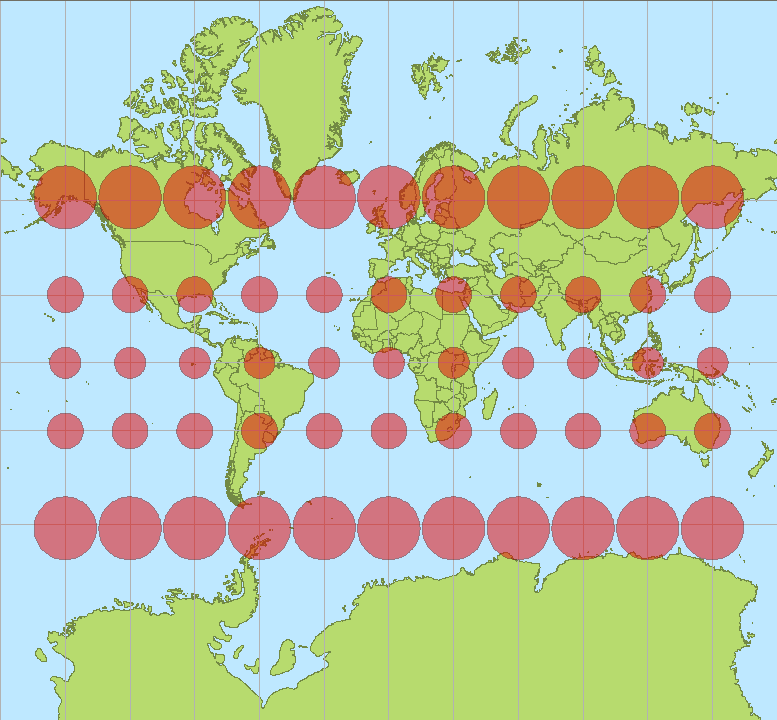
니콜라 티소는 지도 투영의 한 점에서 ''h''와 ''k''로 지정된 척도계수가 그 점에 타원을 정의한다는 것을 알아냈다. 원통 투영의 경우, 타원의 축은 자오선과 평행선에 정렬된다. 메르카토르 투영의 경우, ''h'' = ''k''이므로 타원은 그 위도의 척도계수 값에 비례하는 반지름을 가진 원으로 축퇴된다. 이 원들은 메르카토르의 척도 변화를 나타내는 크기가 극단적으로 다양하게 투영된 지도에 표현된다.

세계 지도 수준의 광역 지도의 경우 적도 상의 축척을 그 지도의 축척으로 표시하는 경우가 많지만, 축척의 변화가 너무 크기 때문에 위도별 축척을 표기하는 경우도 많다.

해도처럼 비교적 제한된 범위를 그리는 경우에는 “1/1,000,000(북위 35도)”와 같이 위도를 지정하여 축척을 표시한다. 더 좁은 범위의 경우에는 지도의 중앙 등 도면 중의 정해진 지점의 축척을 표시한다.(충분히 좁은 경우에는 축척의 변화를 무시할 수 있다). 적도를 축척의 기준으로 하는 경우를 접원통형(tangent type), 적도 이외의 위도를 축척의 기준으로 하는 경우를 할원통형(secant type)이라고 부르는 경우가 있다.

짧은 거리의 간이적인 측정 방법으로는, 지도상에서 길이를 측정하고, 그 길이를 같은 위도 부근에서 경선 방향으로 하여, 위도 차가 몇 도에 해당하는지 확인하고, 1도당 자오선 호장을 약 111km(1분당 1해리)로 환산한다.

가로 메르카토르 도법이나 사축 메르카토르 도법처럼 위도만 또는 경도만으로 간단하게 축척 변화를 표현할 수 없는 경우, 표기 축척에 대해 기준선의 축척을 얼마나 작게 할지를 축척 계수로 지정한다. 다만 이러한 도법은 비교적 큰 축척으로 사용되므로, 정밀한 측정을 하지 않는다면 의식할 필요는 없다.

4. 5. 타원체 모델

지구가 지구타원체(회전타원체)로 모델링될 때, 메르카토르 투영은 각도를 보존하는 사상으로 남아 있으려면 수정되어야 한다.^[24] 변환 방정식과 축척 계수는 다음과 같다.

x = R ( λ - λ₀ ),

y = R ln [tan (π/4 + φ/2) ((1 - esinφ)/(1 + esinφ))^e/2] = R(sinh^-1(tanφ) - etanh^-1(esinφ)),

k = secφ√(1 - e²sin²φ).

축척 계수는 적도에서 1이며, 원통이 적도에서 타원체에 접하기 때문에 반드시 그래야 한다. 타원체 보정 축척 계수는 위도에 따라 증가하지만, ''e''²보다 크지 않으며, 1% 미만의 보정이다. (모든 기준 타원체에 대해 ''e''²의 값은 약 0.006이다.) 이는 적도 근처를 제외하고는 축척 부정확성보다 훨씬 작다. 적도 근처 지역의 정확한 메르카토르 투영만 타원체 보정이 필요하다.

등각 위도가 포함되어 있기 때문에 역변환은 반복적으로 계산된다.

5. 활용

인쇄된 해도는 거의 모두 항해에 유리한 고유한 특성 때문에 메르카토르 도법을 기반으로 한다. 또한 인터넷에서 호스팅되는 도로 지도 서비스에서도 주문형으로 계산되는 지역 지도에 유리한 고유한 특성 때문에 일반적으로 사용된다.^[16] 메르카토르 도법은 1960년대 판구조론의 수학적 발전에도 중요한 역할을 했다.^[17]

리스본(포르투갈)과 아바나(쿠바) 사이의 등각 항로(파란색)와 대권(빨간색) 비교. 위: 정사투영. 아래: 메르카토르 도법.

== 해상 항해 ==

메르카토르 도법은 일정한 방위의 항로를 직선으로 나타내는 고유한 특성 때문에 해상 항해에 사용하도록 설계되었다. 이러한 항로는 등각항로(또는 럼브 라인 또는 록소드롬이라고도 함)로 알려져 있으며, 선박이 일정한 나침반 방향으로 항해할 수 있기 때문에 해상 항해에서 선호된다. 이는 다른 항로를 항해할 때 필요한 어렵고 오류가 발생하기 쉬운 항로 수정을 줄여준다.

짧은 거리(지구 반지름에 비해)의 경우, 등각항로와 대권 항로 간의 차이는 무시할 수 있다. 더 먼 거리의 경우에도 일정한 방위의 단순성 때문에 매력적이다. 메르카토르가 관찰한 바와 같이, 이러한 항로에서는 최단 경로로 도착하지 않지만, 반드시 도착한다. 등각항로를 항해한다는 것은 선원들이 출발할 때 위치, 도착할 때 위치를 알고 메르카토르 도법으로 이 두 좌표를 정확하게 나타내는 지도만 있으면 일정한 항로를 유지하기만 하면 된다는 것을 의미했다.

== 웹 메르카토르 도법 ==

많은 주요 온라인 지도 서비스(빙 맵, 구글 지도, 맵박스, 맵퀘스트, 오픈스트리트맵, 야후! 지도 등)에서 지도 이미지에 메르카토르 투영법의 변형인 웹 메르카토르 또는 구글 웹 메르카토르를 사용한다.^[18] 전 세계 수준(소규모)에서는 눈에 띄는 축척 변화가 있지만, 이 투영법은 상대적으로 왜곡이 거의 없는 변형 투영법의 준각거리 보존성으로 인해 지역(대규모) 지도까지 원활하게 확대할 수 있는 대화형 세계 지도로 적합하다.

주요 온라인 지도 서비스의 타일 시스템은 최저 배율에서 세계 대부분을 단일 정사각형 이미지로 표시하며, 위도 ''φ''_max = ±85.05113°에서 잘라내어 극지방을 제외한다. 이 범위를 벗어난 위도 값은 ''φ'' = ±90°에서 발산하지 않는 다른 관계를 사용하여 매핑된다.

== 횡축 및 사축 메르카토르 도법 ==

횡단 메르카토르 도법은 원통의 축을 지구의 축에 수직이 되도록 기울인 것이다. 따라서 접선 표준선은 자오선 및 그 반대편 자오선과 일치하게 되어 해당 자오선을 따라 일정한 축척계수를 가지며, 주로 남북 방향으로 넓게 펼쳐진 지역을 매핑하는 데 유용하다.^[19] 타원체 형태에서 세계 대부분의 국가 격자 시스템과 UTM 좌표계가 횡단 메르카토르 도법을 사용한다.

프랑스 파리의 개선문에서 2.38m 남쪽에 축(화면 오른쪽 밖)을 둔 사경 메르카토르 투영. 로그 발산으로 인해 직사각형 기념물이 타원형으로 보이며, 원형 교차로의 12개 방사형 도로가 평행하게 나타난다.

사경 메르카토르 투영은 원통 축을 지구 축에서 사용자가 선택한 각도로 기울인다. 따라서 접선 또는 할선 접촉선은 지구의 위도선에 대해 기울어진 원이 된다.^[20] 국가 격자 시스템과 같은 사경 투영의 실용적인 용도는 원통 축의 표면 투영을 따라 축척 변화를 낮게 유지하기 위해 사경 메르카토르의 타원체 개발을 사용하는 것이다.

일반적으로 "메르카토르 도법"이라고 하면 적도를 기준선으로 하여 남북으로 멀어질수록 확대되는 도법을 가리키지만, 다른 대원도 기준선으로 할 수 있다. 자오선을 기준선으로 한 것을 횡메르카토르도법, 그 이외의 대원을 기준선으로 한 것을 사축 메르카토르 도법이라고 한다. 지구를 회전타원체로 고려한 횡메르카토르도법은 특히 가우스-크뤼거 도법이라고도 불린다. 이들은 일반적인 메르카토르 도법(원통도법)의 "경선과 위선이 직교하는 직선인" 성질이 사라지기 때문에, 소축척의 세계지도에는 거의 사용되지 않는다. 그러나 다른 정각도법인 평사도법이나 람베르트 정각원추도법과 비교하면, 기준선이 직선이 되고, 그 기준선과 평행한 직선상에서 축척이 같다는 장점이 있다. 따라서 지형도 등 중축척~대축척 지도의 도법으로서, 대상 지역 근처에 기준선을 설정하고, 기준선 근방의 매우 좁은 범위에 한정하여 사용되는 경우가 많다(유니버설 횡메르카토르 도법 참조).

5. 1. 해상 항해

메르카토르 도법은 일정한 방위의 항로를 직선으로 나타내는 고유한 특성 때문에 해상 항해에 사용하도록 설계되었다. 이러한 항로는 등각항로(또는 럼브 라인 또는 록소드롬이라고도 함)로 알려져 있으며, 선박이 일정한 나침반 방향으로 항해할 수 있기 때문에 해상 항해에서 선호된다. 이는 다른 항로를 항해할 때 필요한 어렵고 오류가 발생하기 쉬운 항로 수정을 줄여준다.

짧은 거리(지구 반지름에 비해)의 경우, 등각항로와 대권 항로 간의 차이는 무시할 수 있다. 더 먼 거리의 경우에도 일정한 방위의 단순성 때문에 매력적이다. 메르카토르가 관찰한 바와 같이, 이러한 항로에서는 최단 경로로 도착하지 않지만, 반드시 도착한다. 등각항로를 항해한다는 것은 선원들이 출발할 때 위치, 도착할 때 위치를 알고 메르카토르 도법으로 이 두 좌표를 정확하게 나타내는 지도만 있으면 일정한 항로를 유지하기만 하면 된다는 것을 의미했다.

5. 2. 웹 메르카토르 도법

많은 주요 온라인 지도 서비스(빙 맵, 구글 지도, 맵박스, 맵퀘스트, 오픈스트리트맵, 야후! 지도 등)에서 지도 이미지에 메르카토르 투영법의 변형인 웹 메르카토르 또는 구글 웹 메르카토르를 사용한다.^[18] 전 세계 수준(소규모)에서는 눈에 띄는 축척 변화가 있지만, 이 투영법은 상대적으로 왜곡이 거의 없는 변형 투영법의 준각거리 보존성으로 인해 지역(대규모) 지도까지 원활하게 확대할 수 있는 대화형 세계 지도로 적합하다.

주요 온라인 지도 서비스의 타일 시스템은 최저 배율에서 세계 대부분을 단일 정사각형 이미지로 표시하며, 위도 ''φ''_max = ±85.05113°에서 잘라내어 극지방을 제외한다. 이 범위를 벗어난 위도 값은 ''φ'' = ±90°에서 발산하지 않는 다른 관계를 사용하여 매핑된다.

5. 3. 횡축 및 사축 메르카토르 도법

횡단 메르카토르 도법은 원통의 축을 지구의 축에 수직이 되도록 기울인 것이다. 따라서 접선 표준선은 자오선 및 그 반대편 자오선과 일치하게 되어 해당 자오선을 따라 일정한 축척계수를 가지며, 주로 남북 방향으로 넓게 펼쳐진 지역을 매핑하는 데 유용하다.^[19] 타원체 형태에서 세계 대부분의 국가 격자 시스템과 UTM 좌표계가 횡단 메르카토르 도법을 사용한다.

사경 메르카토르 투영은 원통 축을 지구 축에서 사용자가 선택한 각도로 기울인다. 따라서 접선 또는 할선 접촉선은 지구의 위도선에 대해 기울어진 원이 된다.^[20] 국가 격자 시스템과 같은 사경 투영의 실용적인 용도는 원통 축의 표면 투영을 따라 축척 변화를 낮게 유지하기 위해 사경 메르카토르의 타원체 개발을 사용하는 것이다.

일반적으로 "메르카토르 도법"이라고 하면 적도를 기준선으로 하여 남북으로 멀어질수록 확대되는 도법을 가리키지만, 다른 대원도 기준선으로 할 수 있다. 자오선을 기준선으로 한 것을 횡메르카토르도법, 그 이외의 대원을 기준선으로 한 것을 사축 메르카토르 도법이라고 한다. 지구를 회전타원체로 고려한 횡메르카토르도법은 특히 가우스-크뤼거 도법이라고도 불린다. 이들은 일반적인 메르카토르 도법(원통도법)의 "경선과 위선이 직교하는 직선인" 성질이 사라지기 때문에, 소축척의 세계지도에는 거의 사용되지 않는다. 그러나 다른 정각도법인 평사도법이나 람베르트 정각원추도법과 비교하면, 기준선이 직선이 되고, 그 기준선과 평행한 직선상에서 축척이 같다는 장점이 있다. 따라서 지형도 등 중축척~대축척 지도의 도법으로서, 대상 지역 근처에 기준선을 설정하고, 기준선 근방의 매우 좁은 범위에 한정하여 사용되는 경우가 많다(유니버설 횡메르카토르 도법 참조).

6. 비판

모든 지도 투영법은 지구 표면의 실제 배치를 형태나 크기 면에서 왜곡한다. 메르카토르 도법은 적도에서 멀리 떨어진 지역의 면적을 과장하며, 극에 가까워질수록 왜곡이 커진다.^[10] 예를 들어 그린란드는 아프리카와 같은 크기로 보이지만, 실제로는 아프리카가 그린란드보다 14배 더 크다. 그린란드의 실제 면적은 콩고 민주 공화국과 비슷하다. 알래스카는 오스트레일리아와 비슷한 크기로 보이지만, 실제로는 오스트레일리아가 4.5배 더 크다. 마다가스카르와 그레이트브리튼은 거의 같은 크기로 보이지만, 마다가스카르가 두 배 이상 크다.^[10]

이러한 육지 면적의 심한 왜곡 때문에 조지 켈러웨이(George Kellaway)와 어빙 피셔(Irving Fisher) 등은 이 투영법이 일반적인 세계 지도에 적합하지 않다고 비판했다. 적도 부근 국가들이 유럽과 북미 국가들에 비해 지나치게 작게 표시되어, 사람들이 이들 국가를 덜 중요하게 여기도록 만들었다는 추측도 있다.^[11] 메르카토르 자신은 상대적인 면적을 나타내기 위해 등적도법인 사인곡선 투영법을 사용했다.

1940년대부터 많은 지도첩에서 적도에서 멀리 떨어진 지역이나 세계 지도에 메르카토르 투영법 대신 다른 원통도법이나 등적 투영법을 선호하게 되었다. 그러나 메르카토르 투영법은 왜곡이 최소화되는 적도 부근 지역의 지도에는 여전히 흔하게 사용된다.

아르노 페터스(Arno Peters)는 1972년부터 메르카토르 투영법의 문제점을 해결하기 위해 현재 갈-페터스 투영법이라고 불리는 투영법을 제안하며 논쟁을 불러일으켰다. 그는 자신의 독창적인 작업이라고 주장했지만, 이는 원통 등적 투영법의 특정 매개변수화였다. 1989년 북미의 7개 지리학 단체는 세계 지도에 원통 투영법을 사용하는 것을 반대하는 결의안을 채택했다.^[15]

참조

_[1] 서적 Science and Civilization in China Cambridge University Press
_[2] 학술지 Projection Methods in Chinese, Korean and Japanese Star Maps
_[3] 학술지 The Chart that Made Navigation History
_[4] 학술지 The Premedieval Origin of Portolan Charts: New Geodetic Evidence
_[5] 학술지 The Premedieval Origin of Portolan Charts: New Geodetic Evidence
_[6] 서적 Mercator: the man who mapped the planet Weidenfeld & Nicolson
_[7] 학술지 Globes, Rhumb Tables, and the Pre-History of the Mercator Projection https://www.tandfonl[...] 2014-07-03
_[8] 학술지 A problem in 'Basic Cartography'
_[9] 학술지 An application of geography to mathematics: history of the integral of the secant https://www.jstor.or[...] 2022-08-18
_[10] 웹사이트 This animated map shows the true size of each country https://www.nature.c[...] 2023-06-20
_[11] 웹사이트 Mercator Projection vs. Peters Projection, part 1 http://geography.abo[...] Matt T. Rosenberg, about.com
_[12] 서적 Map Projections Methuen & Co. LTD
_[13] 서적 Common Map Projections W.H. Smith & Sons
_[14] 서적 The Round Earth on Flat Paper The National Geographic Society
_[15] 학술지
_[16] 웹사이트 Why Mercator for the Web? Isn’t the Mercator bad? https://www.mapthema[...] 2024-11-12
_[17] 서적 Plate Tectonics and Geomagnetic Reversals W.H. Freeman
_[18] 학술지 Implications of Web Mercator and Its Use in Online Mapping http://dx.doi.org/10[...] 2014-06-01
_[19] 웹사이트 Mercator: Extreme https://mrgris.com/p[...]
_[20] 웹사이트 Mercator Projection https://mathworld.wo[...]
_[21] 문서 Snyder. Working Manual, page 20.
_[22] 웹사이트 NIST. See Sections 4.26#ii and 4.23#viii https://dlmf.nist.go[...]
_[23] 서적
_[24] 서적
_[25] 웹사이트 Googleマップの投影法インターネット時代におけるメルカトル図法の再評価 http://user.numazu-c[...] 2016-09-28
_[26] 문서 spherical Mercator Projectionとも呼ばれる。
_[27] 질문응답
_[28] 문서 Weierstrass substitution

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com