맨위로가기

분자 궤도

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

분자 궤도는 원자 궤도의 상호 작용으로 형성되며, 분자 내 전자의 거동을 설명하는 데 사용되는 개념이다. 분자 궤도 이론은 원자 궤도의 선형 결합(LCAO)을 통해 분자 궤도를 계산하며, 분자 궤도는 결합성, 반결합성, 비결합성 궤도로 분류된다. 분자 궤도는 분자 궤도 다이어그램을 통해 시각화되며, 분자 궤도의 에너지 준위와 전자의 배치를 나타낸다. 분자 궤도 이론은 분자의 결합 차수, HOMO-LUMO 갭, 그리고 화학 반응의 예측과 해석에 활용된다.

2. 분자 오비탈의 형성

분자 궤도(MO)는 전자가 발견될 가능성이 있는 분자 내 영역을 나타낸다. 분자 궤도는 분자를 구성하는 원자들의 원자 궤도들이 상호작용하여 형성된다. 이러한 상호작용은 원자 궤도들의 대칭성이 서로 맞을 때 가능하며, 군론을 통해 결정된다.[4] 원자 궤도 상호 작용의 효율은 두 원자 궤도 간의 겹침(overlap)에 의해 결정되는데, 이는 원자 궤도의 에너지가 서로 비슷할 때 커진다. 최종적으로, 분자 궤도의 수는 결합에 참여하는 원자 궤도의 수와 같다.

분자 궤도는 분자의 전자 배치(하나의 전자 또는 전자쌍의 공간 분포 및 에너지)를 설명해준다. 보통 원자 궤도 함수의 선형 결합으로 표현되는데, 이는 분자 내 결합을 이해하는 데 유용한 간단한 모델을 제공한다. 계산 화학의 현대적인 방법들은 대부분 계의 분자 궤도를 계산하는 것으로 시작한다. 분자 궤도는 원자핵과 다른 전자들의 평균적인 분포에 의해 생성된 전기장 내에서 하나의 전자가 어떻게 움직이는지를 나타낸다. 만약 두 전자가 같은 궤도를 점유한다면, 파울리 배타 원리에 따라 이들은 서로 반대 스핀을 가져야 한다. 그러나 분자 전자 파동 함수에 대한 매우 정확한 묘사는 궤도를 갖지 않는다. (배치간 상호작용 참조)

2. 1. 원자 궤도 함수 선형 결합 (LCAO)

분자 궤도는 원자 궤도의 결합으로 얻어지며, 분자 내에서 하나의 전자 또는 한 쌍의 전자가 발견될 수 있는 영역을 나타낸다. 흔히 분자 궤도는 원자 궤도 함수 선형 결합(LCAO-MO method)으로 표현되는데, 이는 매우 정성적인 방법이지만 분자 내 결합 모델을 이해하는 데 유용하다.

정성적으로 유용한 분자 구조 논의를 위해, 분자 궤도는 '원자 궤도 함수 선형 결합'(LCAO) 또는 '보른-오펜하이머 근사법'을 통해 얻을 수 있다. LCAO는 분자 궤도를 계산하는 방법으로, 원자 궤도가 기초 함수를 이루기 때문에 분자 궤도를 원자 궤도의 무한 합으로 표현할 수 있다. 이는 임의의 함수를 테일러 전개하는 것과 같은 원리이다. LCAO 자체는 근사법이 아니며 수학적으로 정당하다.[46]

분자 궤도를 LCAO로 전개한 뒤 적절한 주요 항(주로 2개)을 제외하고 모두 제거하는 방식으로 근사한다.

:

\psi_i = \sum_r c_{ri} \psi_i = c_{1i}\psi_i+c_{2i}\psi_i+c_{3i}\psi_i+...



위 식에서 c_{ri}는 각 원자 궤도가 분자 궤도에 얼마나 기여했는가를 나타내는 기여도로, 하트리-폭 근사법을 통해 결정된다.

1929년 존 레너드-존스 경이 H와 He의 조합으로 이중분자를 만들고, 이 결합을 표현하기 위해 LCAO를 발표하였는데, 라이너스 폴링의 경우 H2분자를 계산하면서 이보다 앞서서 이 방법을 사용하였다.[47]

하지만 컴퓨터 화학의 발달 이후 LCAO는 최적화된 파동함수로 여겨지지 않게 되었다. 대신 현대적인 방법으로 얻은 결과를 예측하고 합리화하는데 유용한 정성적인 분석의 수단으로 여겨진다.

원자 궤도 함수의 선형 결합(LCAO)은 분자를 구성하는 원자 간의 결합 시 형성되는 분자 궤도를 추정하는 데 사용될 수 있다. 간단한 이원자 분자의 경우, 얻어진 파동 함수는 다음과 같은 방정식으로 수학적으로 표현된다.

:\Psi = c_a \psi_a + c_b \psi_b

:\Psi^* = c_a \psi_a - c_b \psi_b

여기서 \Psi와 \Psi^*는 각각 결합성 및 반결합성 분자 궤도에 대한 분자 파동 함수이고, \psi_a와 \psi_b는 각각 원자 a와 b의 원자 파동 함수이며, c_a와 c_b는 조정 가능한 계수이다. 이 계수는 개별 원자 궤도의 에너지와 대칭에 따라 양수 또는 음수가 될 수 있다. 두 원자가 가까워질수록 원자 궤도가 겹쳐 전자 밀도가 높은 영역을 생성하며, 그 결과 두 원자 사이에 분자 궤도가 형성된다.

2. 2. 보른-오펜하이머 근사

분자 궤도는 정성적으로 유용한 분자 구조를 논의하기 위해 '원자 궤도 함수 선형 결합'(LCAO) 또는 '보른-오펜하이머 근사'를 통해 얻을 수 있다. 비록 정성적인 방법이지만, 분자 내 간단한 결합 모델을 이해하는 데 매우 유용하다.[44]

보른-오펜하이머 근사는 전자의 운동과 핵의 운동을 분리할 수 있다는 가설이다. 즉, 분자의 파동함수를 전자의 파동함수와 핵의 파동함수로 분리할 수 있다는 뜻이다. 핵의 질량이 전자의 질량보다 훨씬 무겁기 때문에(약 1833배) 핵의 위치는 정지해 있다고 가정한다. 이를 식으로 표현하면 다음과 같다.

:

\psi_{molecule} (\vec r_{i},\vec R_{j}) = \psi_{electrons}(\vec r_{i}, \vec R_{j}) \times \psi_{nuclei}(\vec R_{j})



이 근사를 설명하기 위해 가장 간단한 분자인 H_2 ^{+}를 예로 들 수 있다. 두 핵 사이의 거리를 R_{AB}라 하고, 전자와 핵 사이의 거리를 각각 r_a, r_b라 할 때, 이 분자의 위치 에너지는 다음과 같다.

:

V(R_{AB}) = \frac{e^2}{4 \pi \epsilon _{0} R_{AB}} - \frac{e^2}{4 \pi \epsilon _{0} r_{A}} - \frac{e^2}{4 \pi \epsilon _{0} r_{B}}



위치 에너지 값을 바꿔가며 그래프를 그려보면, 반발력이 최소가 되는 지점에서 두 원자가 결합하게 된다. 이때의 값을 분자 핵간 거리라고 하며, 이는 보른-오펜하이머 근사를 통해 두 원자가 결합하여 분자를 만들 때 핵 사이의 거리가 일정하기 때문에 얻을 수 있는 결과이다.

3. 분자 오비탈의 종류

분자 오비탈은 원자 오비탈의 결합으로 얻어지며, 분자 내에서 전자가 발견될 수 있는 영역을 나타낸다. 분자 오비탈은 분자 내 전자 배치에 대한 정보를 제공하며, 주로 원자 오비탈의 선형 결합(LCAO-MO)으로 표현된다.

분자 궤도는 일반적으로 분자 전체에 비편재화되어 있으며, 분자가 대칭 요소를 갖는 경우 대칭 또는 반대칭성을 갖는다. 예를 들어 평면 분자에서 분자 궤도는 분자 평면에 대한 반사에 대해 대칭(σ)이거나 반대칭(π)이다.

분자 오비탈은 (\sigma_{u1s}^*)^1과 같은 형태로 나타낼 수 있다. 여기서 각 기호의 의미는 다음과 같다.


  • σ와 π: 핵간 축 주위의 각운동량 성분을 나타낸다.
  • 아래 첨자 g와 u: 분자 중심에 대한 대칭성을 나타낸다. (g: geradede, 짝수), (u: ungeradede, 홀수)
  • *: 반결합 오비탈을 나타낸다.
  • 아래 첨자 (g, u 옆): MO에 참여한 원자 오비탈(AO)의 종류를 나타낸다.
  • 위 첨자 (괄호 바깥): MO에 있는 전자 수를 나타낸다.

3. 1. 결합성, 반결합성, 비결합성 분자 오비탈

원자 궤도가 상호 작용할 때, 생성되는 분자 궤도는 결합성, 반결합성, 비결합성의 세 가지 유형이 될 수 있다.

  • 결합성 분자 궤도(Bonding MO):
  • 원자 궤도 간의 결합 상호 작용은 건설적인 (동위상) 상호 작용이다.
  • 결합성 분자 궤도는 이를 생성하는 원자 궤도보다 에너지가 낮다.
  • 반결합성 분자 궤도(Antibonding MO):
  • 원자 궤도 사이의 반결합 상호 작용은 파괴적인 (역위상) 상호 작용으로, 상호 작용하는 두 원자 사이의 반결합 궤도의 파동 함수가 0인 마디면을 갖는다.
  • 반결합성 분자 궤도는 이를 생성하는 원자 궤도보다 에너지가 높다.
  • 비결합성 궤도(Nonbonding MO):
  • 비결합성 분자 궤도는 호환되는 대칭성이 부족하여 원자 궤도 사이의 상호 작용이 없는 결과이다.
  • 비결합성 분자 궤도는 분자 내 한 원자의 원자 궤도와 동일한 에너지를 갖는다.

3. 2. 분자 오비탈의 대칭성

분자가 대칭 요소를 갖는다면, 비축퇴 분자 궤도는 이러한 대칭 중 어느 하나에 대해 대칭이거나 반대칭이다. 즉, 분자 궤도 ψ에 대칭 연산 S (반사, 회전 또는 반전)를 적용하면 분자 궤도가 변경되지 않거나 부호가 역전된다. : Sψ = ± ψ. 평면 분자에서, 분자 궤도는 분자 평면에서 반사와 관련하여 대칭 (σ) 또는 반 대칭 (π) 중 하나이다. 축퇴된 궤도 에너지를 가진 분자들도 고려한다면, 분자 궤도가 분자 대칭 그룹의 환원 불가능한 표현에 대한 기초를 형성한다는 보다 일반적인 진술이있다.[44] 분자 오비탈의 대칭성은 비편재화가 분자 궤도 이론의 고유한 특징이며, 결합을 편재화된 전자쌍으로 보는 원자가 결합 이론과 근본적으로 다르다.

분자 오비탈은 (\sigma_{u1s}^*)^1 형태로 나타낼 수 있고 각 분자 오비탈의 이름은 다음과 같이 정해진다.[45]

  • \sigma와 \pi는 핵간 축 주위의 전자에 대한 각운동량 성분을 나타낸다. 핵간 축에 수직인 평면에서 봤을 때 축 주위에 전자 밀도가 어떻게 분포되어 있는지를 말해준다. \sigma와 \pi가 나타내는 각운동량의 값은 다음과 같다.
  • * \sigma : 각운동량 성분 = 0
  • * \pi : 각운동량 성분 = \pm \frac {h} {2\pi}
  • 아래 첨자 g,u는 관찰점을 분자 중심에 대하여 뒤집을 때, 파동함수의 특이성이 어떻게 변화하는지를 설명한다. 분자의 중심을 기준으로 대칭이면 g(geradede : 짝수), 비대칭이면 u(ungeradede : 홀수)로 표기한다. 원점을 분자 중심에 놓은 데카르트 좌표에서 (x,y,z)와 (-x,-y,-z)의 점의 파동함수를 비교하면 된다. 파동함수의 부호가 동일하면 g, 다르면 u로 표기한다.
  • *는 반결합 오비탈을 표시한다. 결합 MO의 경우는 공란, 반결합 MO (anti-bonding MO)의 경우에 * 표시를 한다. 반결합 오비탈은 핵 사이에 훨씬 적은 전자 밀도를 가지며, 밀도는 핵간의 마디에서 0이 된다.
  • g 또는 u 바로 옆에 아래첨자로 표기된 문자는 MO에 참여한 AO(atomic orbital)의 종류를 의미한다.
  • 괄호 바깥에 위첨자로 표기된 숫자는 MO에 있는 전자수를 의미한다.


원자 궤도 사이의 상호 작용 유형은 분자 궤도 대칭 라벨 σ(시그마), π(파이), δ(델타), φ(파이), γ(감마) 등으로 더욱 세분화될 수 있다. 이는 각각 원자 궤도 s, p, d, f, g에 해당하는 그리스 문자이다. 관련된 원자 사이의 핵간 축을 포함하는 마디 평면의 수는 σ 분자 궤도의 경우 0개, π의 경우 1개, δ의 경우 2개, φ의 경우 3개, γ의 경우 4개이다.

σ 대칭성을 가진 분자 궤도는 두 개의 원자 s-궤도함수 또는 두 개의 원자 pz-궤도함수의 상호 작용으로 발생한다. 분자 궤도는 두 핵 중심을 연결하는 축, 즉 핵간 축에 대해 대칭이면 σ-대칭성을 갖는다. 핵간 축을 중심으로 분자 궤도를 회전시켜도 위상 변화가 일어나지 않는다. σ* 궤도 함수, 즉 시그마 반결합 궤도 함수 역시 핵간 축을 중심으로 회전할 때 동일한 위상을 유지한다. σ* 궤도 함수는 핵 사이에 있고 핵간 축에 수직인 마디면을 갖는다.[14]

π 대칭을 갖는 분자 궤도는 두 개의 원자 px 오비탈 또는 py 오비탈의 상호작용의 결과로 나타난다. 분자 궤도가 핵간 축에 대한 회전에 대해 비대칭적이면 π 대칭을 갖는다. 핵간 축에 대해 분자 궤도를 회전시키면 위상 변화가 발생한다. 실제 오비탈을 고려할 경우, 핵간 축을 포함하는 하나의 마디면이 존재한다.

π* 오비탈, 즉 파이 반결합 오비탈 역시 핵간 축을 중심으로 회전할 때 위상 변화를 일으킨다. π* 오비탈은 또한 핵 사이에 두 번째 마디면을 갖는다.

δ 대칭을 갖는 분자 궤도는 두 개의 원자 dxy 또는 dx2-y2 오비탈의 상호 작용으로 생성된다. 이러한 분자 궤도는 저에너지 d 원자 궤도를 포함하므로, 전이 금속 착물에서 관찰된다. δ 결합성 오비탈은 핵간 축을 포함하는 두 개의 마디면을 가지며, δ* 반결합성 오비탈은 핵 사이에 세 번째 마디면을 갖는다.

이론 화학자들은 f 원자 궤도의 겹침에 해당하는 파이 결합과 같은 고차 결합이 가능하다고 추측해 왔다. 파이 결합을 포함하는 것으로 추정되는 분자의 알려진 예는 없다.

대칭 중심(대칭 중심 분자)을 갖는 분자의 경우, 분자 궤도 함수에 적용할 수 있는 추가적인 대칭 라벨이 있다.

대칭 중심 분자에는 다음이 포함된다.

  • 동핵 이원자 분자, X₂
  • 팔면체, EX₆
  • 정사각형 평면, EX₄.


비대칭 중심 분자에는 다음이 포함된다.

  • 이핵 이원자 분자, XY
  • 사면체, EX₄.


분자 내의 대칭 중심을 통한 반전이 분자 궤도 함수에 동일한 위상을 생성하는 경우, 해당 분자 궤도 함수는 게레데(g) 대칭을 갖는다고 한다.

분자 내의 대칭 중심을 통한 반전이 분자 궤도 함수의 위상 변화를 생성하는 경우, 해당 분자 궤도 함수는 운게레데(u) 대칭을 갖는다고 한다.

σ-대칭을 갖는 결합 분자 궤도 함수의 경우, 궤도 함수는 σg이다; 반면 σ-대칭을 갖는 반결합 분자 궤도 함수의 경우 궤도 함수는 σu이다.

π-대칭을 갖는 결합 분자 궤도 함수의 경우, 궤도 함수는 πu인데, 대칭 중심을 통한 반전이 부호 변화를 생성하기 때문이다(두 p 원자 궤도 함수는 서로 위상이 같지만 두 로브는 반대 부호를 가짐). 반면 π-대칭을 갖는 반결합 분자 궤도 함수의 경우, 궤도 함수는 πg인데, 대칭 중심을 통한 반전이 부호 변화를 생성하지 않기 때문이다.[1]

4. 분자 오비탈 다이어그램

분자 궤도 이론에서 분자 내 결합 상호작용을 시각적으로 나타내기 위해 분자 궤도 다이어그램이 사용된다. 이 다이어그램에서 분자 궤도는 가로선으로 표시되며, 선이 높을수록 궤도의 에너지가 높다는 것을 의미한다. 축퇴된 궤도는 간격을 두고 같은 높이에 배치된다. 파울리 배타 원리 및 훈트 규칙(각 궤도당 반대 스핀을 가진 전자 2개만 허용, 짝을 이루기 전에 가능한 한 많은 비대칭 전자를 한 에너지 수준에 배치)에 따라 전자를 분자 궤도에 하나씩 채워 나간다.

분자 궤도 다이어그램을 구성하는 일반적인 절차는 다음과 같다.


  • 궤도 기저 집합은 결합 또는 반결합일 수 있는 분자 궤도 상호 작용에 사용할 수 있는 원자 궤도를 포함한다.
  • 분자 궤도의 수는 선형 확장 또는 기저 집합에 포함된 원자 궤도의 수와 같다.
  • 분자가 어느 정도의 대칭성을 가지고 있다면, 축퇴된 원자 궤도(동일한 원자 에너지)는 표현의 대칭군에 속하는 선형 결합('''대칭 적응 원자 궤도(SO)''')으로 그룹화되므로, 이 그룹을 설명하는 파동 함수는 '''대칭 적응 선형 결합''' ('''SALC''')으로 알려져 있다.
  • 하나의 그룹 표현에 속하는 분자 궤도의 수는 이 표현에 속하는 대칭 적응 원자 궤도의 수와 같다.
  • 특정 표현 내에서 대칭 적응 원자 궤도는 원자 에너지 준위가 가까울수록 더 많이 혼합된다.[4]


더 복잡한 분자의 경우, 파동 역학적 접근 방식은 결합에 대한 질적 이해에서는 효용성을 잃는다(양적 접근 방식에서는 여전히 필요하다).[18]

5. 분자 오비탈과 결합

분자 오비탈(MO)은 전자가 발견될 가능성이 있는 분자 내 영역을 나타내며, 원자 궤도의 결합으로 얻어진다. 분자 오비탈은 분자의 전자 배치, 즉 전자(또는 전자쌍)의 공간 분포와 에너지에 대한 정보를 제공한다. 주로 원자 궤도의 선형 결합(LCAO-MO) 방법으로 표현되며, 이는 분자 내 결합을 이해하는 데 유용하다.

분자 궤도는 일반적으로 분자 전체에 비편재화되어 있으며, 분자가 대칭 요소를 가지면 분자 궤도는 대칭 또는 반대칭이 된다. 예를 들어 평면 분자에서 분자 궤도는 분자 평면에 대해 대칭(시그마 결합)이거나 반대칭(파이 결합)이다.

프리드리히 훈트와 로버트 멀리컨이 1927년과 1928년에 분자 궤도 개념을 처음 도입했으며,[25][26][27][28][29][30][31][32][33][34] 존 레너드-존스는 1929년에 원자 궤도 함수의 선형 결합(LCAO) 근사를 도입하여 플루오린과 산소 분자의 전자 구조를 설명했다.[35]

원자 궤도 함수의 선형 결합(LCAO)은 분자 궤도를 추정하는 데 사용된다. 간단한 이원자 분자에서 파동 함수는 다음과 같이 표현된다.

:\Psi = c_a \psi_a + c_b \psi_b (결합성 분자 궤도)

:\Psi^* = c_a \psi_a - c_b \psi_b (반결합성 분자 궤도)

여기서 \Psi와 \Psi^*는 각각 결합성 및 반결합성 분자 파동 함수, \psi_a와 \psi_b는 원자 a와 b의 원자 파동 함수, c_a와 c_b는 조정 계수이다.

원자 궤도가 상호 작용할 때, 결합성, 반결합성, 비결합성 분자 궤도가 생성될 수 있다.


  • 결합성 MO: 원자 궤도 간의 상호적인(동위상) 상호작용으로, 혼합된 원자 궤도보다 에너지가 낮다.
  • 반결합성 MO: 원자 궤도 간의 상쇄적인(엇갈린 위상) 상호작용으로, 혼합된 원자 궤도보다 에너지가 높다.
  • 비결합성 MO: 원자 궤도 간 상호작용이 없어, 에너지가 변하지 않는다.


이온 결합의 경우, 분자 궤도 이론을 사용하여 극성 결합으로 설명할 수 있다. 결합 궤도는 음이온의 원자 궤도와 에너지 및 특성이 매우 유사하며, 전자가 음이온으로 완전히 이동함을 의미한다.[20]

5. 1. 결합 차수

분자의 결합 차수(또는 결합 수)는 결합성 및 반결합성 분자 궤도에 있는 전자의 수를 결합하여 결정할 수 있다. 결합성 궤도에 있는 전자 쌍은 결합을 생성하는 반면, 반결합성 궤도에 있는 전자 쌍은 결합을 무효화한다. 예를 들어, 결합성 궤도에 8개의 전자와 반결합성 궤도에 2개의 전자를 가진 N2는 결합 차수가 3으로 삼중 결합을 구성한다.[1]

결합 강도는 결합 차수에 비례하며, 더 많은 결합은 더 안정적인 결합을 생성하고, 결합 길이는 결합 차수에 반비례하며, 더 강한 결합은 더 짧다.

분자가 양의 결합 차수를 가져야 한다는 요구 사항에는 드문 예외가 있다. Be2는 분자 궤도 분석에 따르면 결합 차수가 0이지만, 매우 불안정한 Be2 분자가 245pm의 결합 길이와 10kJ/mol의 결합 에너지를 갖는다는 실험적 증거가 있다.[21]

분자의 결합 차수(또는 결합 수)는 결합성 및 반결합성 분자 궤도 내의 전자의 수를 다음과 같이 조합하여 결정할 수 있다.

결합 차수 = 0.5 * [(결합성 궤도 내의 전자 수) - (반결합성 궤도 내의 전자 수)]

예를 들어, 결합성 궤도에 8개의 전자와 반결합성 궤도에 2개의 전자를 가진 N2의 결합 차수는 3이며, 삼중 결합을 구성한다. 결합 길이는 결합 차수에 반비례한다.

Be2는 분자 궤도 함수(MO)에 따르면 결합 차수가 0이 되지만, 결합 길이 245pm, 결합 에너지 10kJ/mol의 매우 불안정한 Be2가 존재한다는 실험적 증거가 있다는 점에 유의해야 한다[37]。

5. 2. HOMO와 LUMO

가장 높은 점유 분자 궤도(Highest Occupied Molecular Orbital, HOMO)와 가장 낮은 비점유 분자 궤도(Lowest Unoccupied Molecular Orbital, LUMO)는 각각 HOMO와 LUMO로 불린다. HOMO와 LUMO의 에너지 차이를 HOMO-LUMO 갭이라고 하며, 이 값은 문헌에서 종종 혼란의 대상이 되므로 주의해야 한다. HOMO-LUMO 갭은 일반적으로 기본 갭(이온화 전위와 전자 친화도의 차이)과 광학 갭 사이에 위치한다. 또한, HOMO-LUMO 갭은 벌크 물질의 띠 간격 또는 수송 갭과 관련될 수 있으며, 이는 일반적으로 기본 갭보다 훨씬 작다.[4]

HOMO와 LUMO의 에너지 차이는 띠틈이라고도 불리며, 분자의 여기성을 나타내는 지표로 사용된다. 에너지 차이가 작을수록 분자는 더 쉽게 여기된다.

6. 분자 오비탈의 예시

H2+ 분자 궤도 도표


분자 오비탈 이론을 통해 H2+의 에너지를 구할 수 있다. 슈뢰딩거 방정식에서 파동방정식의 해는 다음과 같이 표시될 수 있다.

:\Psi =c _{A} \psi _{A} +c _{B} \psi _{B}

H2+의 대칭성에 의해 c _{A}^2=c _{B}^2이다. 계산상의 편의를 위해 c _{A}^2=c _{B}^2=c _{0}^2 라고 하고, S _{AB} = \int _{} ^{} {\psi _{A} ^{*} \psi _{B}} d \tau 를 중첩 적분이라고 정의하면, 파동함수의 정의에 의해 아래와 같은 식이 성립한다.

: \int |\Psi_{0}|^2\, d\tau = 1= c _{0} ^{2} ( \int | \psi _{A} | ^{2} d \tau + \int | \psi _{B} | ^{2} d \tau + \int \psi _{A} ^{*} \psi _{B} d \tau + \int \psi _{A} \psi _{B} ^{*} d \tau)

:=c _{0} ^{2}(1+1+S_{AB}+S_{AB}^{*} = 2c _{0} ^{2}(1+S_{AB})

따라서,

: c_{0}=\left[ 2\left( 1+S_{AB}\right) \right] ^{-\dfrac {1}{2}}

이 때 슈뢰딩거 방정식에서 좌변을 헤밀토니안, 우변을 에너지 항으로 놓는다면 H2+의 에너지는 다음과 같다.

: E _{0} (R)= \int \psi _{0} ^{*} H \psi _{0} d \tau = \frac

{\int \psi _{A} ^{*} H \psi _{A} d \tau + \int \psi _{A} ^{*} H \psi _{B} d \tau

+ \int \psi _{B} ^{*} H \psi _{A} d \tau + \int \psi _{B} ^{*} H \psi _{B} d \tau } {2(1+S _{AB})}

=\frac {H _{AA} +H _{AB} +H _{BA} +H _{BB}} {2(1+S _{AB})}

=\frac {H _{AA} +H _{AB}} {1+S _{AB}}

여기서 최종항에 있는 항은 다음과 같이 나타낼 수 있다.

: H _{AA} = \int {\psi _{A} ^{*}( \frac {p ^{2}} {2m} - \frac {e ^{2}} {4 \pi \epsilon _{0} r _{A}} ) \psi _{A}} d \tau +\frac {e ^{2}} {4 \pi \epsilon _{0} R} \int {\psi _{A} ^{*}} \psi _{A} d \tau - \int{\frac {e ^{2}} {4 \pi \epsilon _{0} r _{B}} \psi _{A} ^{*} \psi _{A} d \tau } =E _{H} (1s)+ \frac {e ^{2}} {4 \pi \epsilon _{0} R} +J



:H _{AB} = \int {\psi _{A} ^{*}( \frac {p ^{2}} {2m} - \frac {e ^{2}} {4 \pi \epsilon _{0} r _{B}} ) \psi _{B}} d \tau +\frac {e ^{2}} {4 \pi \epsilon _{0} R} \int {\psi _{A} ^{*}} \psi _{B} d \tau - \int{\frac {e ^{2}} {4 \pi \epsilon _{0} r _{A}} \psi _{A} ^{*} \psi _{B} d \tau }=\int\psi_{A}^{*}E_{H}(1s)\psi_{B}d\tau+\frac {e ^{2}} {4 \pi \epsilon _{0} R}S_{AB}+K=S_{AB}[E_{H}(1s)+\frac {e ^{2}} {4 \pi \epsilon _{0} R}]+K

또한 이 식에서 J와 K는 다음과 같다.

: J=-\int\frac {e ^{2}} {4 \pi \epsilon _{0} r_{B}}\psi_{A}^{*}\psi_{A}d\tau

: K=-\int\frac {e ^{2}} {4 \pi \epsilon _{0} r_{A}}\psi_{A}^{*}\psi_{B}d\tau

바닥 상태의 오비탈은 \Psi_{0}=\frac {\psi_{A}(1s)+\psi_{B}(1s)}{c_{0}}, 들뜬 상태의 오비탈은 \Psi_{1}=\frac {\psi_{A}(1s)-\psi_{B}(1s)}{c_{0}}로 나타낼 수 있다. 이에 따른 바닥 상태와 들뜬 상태의 에너지 값은 각각 아래와 같다.

:E_{0}( R) =E_{H}\left( 1s\right) +\dfrac {e^{2}}{4\pi \varepsilon _{0}R}+\dfrac {J+K}{1+s_{AB}}

:E_{1}(R)=E_{H}(1s)+\frac{e^{2}}{4\pi\epsilon_{0}R}+\frac{J-K}{1-S_{AB}}

이와 같은 방식으로 다양한 상태의 H2+의 에너지를 구할 수 있다. \Psi =c _{A} \psi _{A} +c _{B} \psi _{B}에서 정확한 파동 함수를 구하기 위해 c_{A}와 c_{B}를 구하면 다음과 같다.

:\begin{pmatrix} \alpha-E & \beta-ES \\ \beta-ES & \alpha-E \end{pmatrix}{n \choose k}=0

위 행렬식을 통해 아래와 같이 나타낼 수 있다.

:c_A \left ( \alpha-E \right) + c_B \left ( \beta-ES \right )=0

:c_A \left ( \beta-ES \right) + c_B \left ( \alpha-E \right )=0

위 두 식을 연립하여 E를 표현하면 다음과 같다.

:E_+ = \frac {\alpha+\beta} {1+S}, E_- = \frac {\alpha-\beta} {1-S}

따라서 E_+ 인 경우 c_A=c_B이며, E_-인 경우 c_A=-c_B가 된다.

\int \psi^2 d\tau = 1 이므로,

: c \approx \frac {1} {\sqrt 2}, (S \approx 0)

: \psi_+ = \frac {1} {\sqrt 2} ( \phi_{AA} + \phi_{AB} ), \psi_- = \frac {1} {\sqrt 2} ( \phi_{AA} - \phi_{AB} )

6. 1. 동핵 이원자 분자

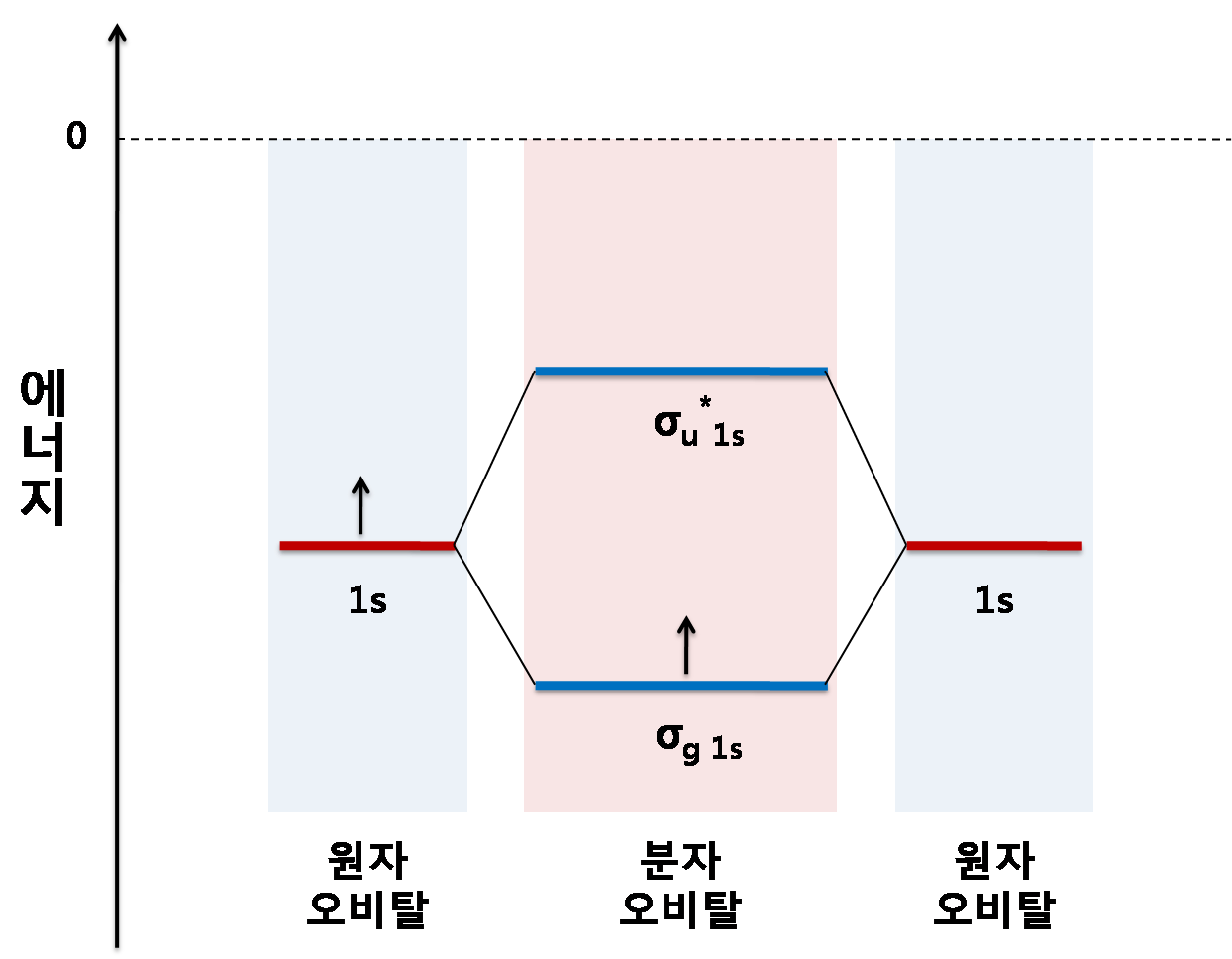
동핵 이원자 분자 궤도 함수(MO)는 기저 집합의 각 원자 궤도 함수에서 동일한 기여를 포함한다. 이는 H2, He2, Li2의 동핵 이원자 MO 다이어그램에 나타나 있으며, 모두 대칭 궤도 함수를 포함한다.[1]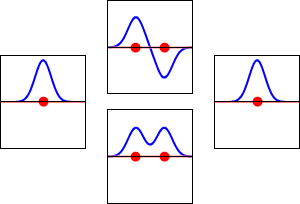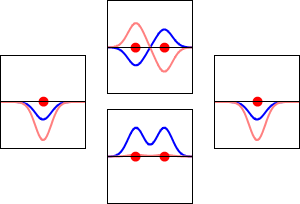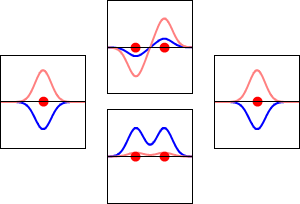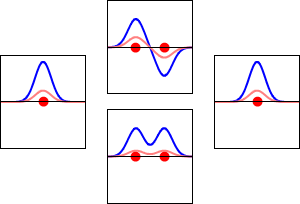

고립된 수소 원자(왼쪽과 오른쪽)의 원자 궤도 파동함수와 H2 분자의 해당 결합성(아래) 및 반결합성(위) 분자 궤도. 파동함수의 실수 부분은 파란색 곡선이고, 허수 부분은 빨간색 곡선이다. 빨간색 점은 핵의 위치를 표시한다. 전자 파동함수는 슈뢰딩거 파동 방정식에 따라 진동하며, 궤도는 그 정상파이다. 정상파 주파수는 궤도의 운동 에너지에 비례한다.


H'과 H"로 표시된 두 개의 원자를 가진 수소 분자 H2(분자 궤도 다이어그램 참조)의 전자를 고려하면, 가장 낮은 에너지의 원자 궤도, 1s' 및 1s"는 분자의 대칭에 따라 변환되지 않는다. 그러나 다음 대칭 적응 원자 궤도가 있다.

1s' – 1s"반대칭 조합: 반사에 의해 부호가 바뀌고 다른 연산에 의해 변경되지 않음
1s' + 1s"대칭 조합: 모든 대칭 연산에 의해 변경되지 않음



대칭 조합(결합성 궤도)은 기본 궤도보다 에너지가 낮고, 반대칭 조합(반결합성 궤도)은 더 높다. H2 분자는 두 개의 전자를 가지고 있기 때문에 둘 다 결합성 궤도로 들어갈 수 있으며, 이는 시스템을 두 개의 자유 수소 원자보다 에너지가 낮게(따라서 더 안정하게) 만든다. 이것을 공유 결합이라고 한다. 결합 차수는 결합성 전자의 수에서 반결합성 전자의 수를 뺀 값을 2로 나눈 값과 같다. 이 예에서는 결합성 궤도에 2개의 전자가 있고 반결합성 궤도에는 전자가 없으므로 결합 차수는 1이고 두 수소 원자 사이에는 단일 결합이 존재한다.

반면에, He'과 He"로 표기된 원자를 가진 가상의 He2 분자를 생각해 보자. H2와 마찬가지로, 가장 낮은 에너지의 원자 궤도는 1s'와 1s"이며, 분자의 대칭성에 따라 변환되지 않지만, 대칭 적응 원자 궤도는 변환된다. H2와 달리 He2는 중성 바닥 상태에서 네 개의 전자를 가지고 있다. 두 개의 전자는 낮은 에너지의 결합 궤도 σg(1s)를 채우고, 나머지 두 개는 더 높은 에너지의 반결합 궤도 σu*(1s)를 채운다. 따라서 분자 주위의 결과적인 전자 밀도는 두 원자 사이의 결합 형성을 지원하지 않으며, 원자를 함께 유지하는 안정적인 결합이 없으면 분자는 존재하지 않을 것으로 예상된다. 결합 차수는 0이며 결합은 존재하지 않는다.

Li2는 두 개의 Li 원자의 1s 및 2s 원자 궤도(기저 세트)의 중첩으로 형성된다. 각 Li 원자는 결합 상호 작용에 세 개의 전자를 제공하며, 여섯 개의 전자는 가장 낮은 에너지의 세 개의 분자 궤도(MO), σg(1s), σu*(1s), σg(2s)를 채운다. 결합 차수에 대한 방정식을 사용하면 Li2의 결합 차수가 1, 즉 단일 결합임을 알 수 있다.[22]

일반적으로 완전한 에너지 껍질을 가진 He와 같은 원자는 다른 원자와 거의 결합하지 않는다. 단명하는 반 데르 발스 복합체를 제외하고는 알려진 비활성 기체 화합물은 거의 없다.

6. 2. 이핵 이원자 분자

이핵 이원자 분자의 분자 궤도는 서로 다른 원자 궤도 기여를 포함한다. 이핵 이원자 분자에서 결합 또는 반결합 궤도를 생성하기 위한 궤도 상호 작용은 대칭성과 궤도 에너지의 유사성에 의해 결정되는 원자 궤도 간에 충분한 중첩이 있는 경우 발생한다.[23]

플루오린화 수소(HF)에서 H 1s와 F 2s 오비탈 사이의 중첩은 대칭에 의해 허용되지만, 두 원자 오비탈 간의 에너지 차이로 인해 분자 오비탈을 생성하기 위한 상호 작용이 방해받는다. H 1s와 F 2pz 오비탈 사이의 중첩 또한 대칭에 의해 허용되며, 이 두 원자 오비탈은 작은 에너지 차이를 갖는다. 따라서, 이들은 상호 작용하여 σ와 σ* 분자 궤도를 생성하고, 결합 차수가 1인 분자를 형성한다. HF는 비중심 대칭 분자이므로, 대칭 라벨 g와 u는 분자 궤도에 적용되지 않는다.[23]

7. 정량적 접근

분자 에너지 준위에 대한 정량적인 값을 얻으려면 배치간 상호작용 (CI) 확장이 full CI 극한으로 빠르게 수렴하는 분자 궤도가 필요하다. 이러한 함수를 얻기 위한 가장 일반적인 방법은 분자 궤도를 포크 연산자의 고유 함수로 표현하는 하트리-포크 방법이다. 이 방법은 일반적으로 원자핵을 중심으로 한 가우스 함수의 선형 결합으로 분자 궤도를 표현함으로써 이 문제를 푼다. (원자 궤도 함수의 선형 결합 및 기저 집합 (화학) 참조). 이러한 선형 결합의 계수를 구하는 문제는 로턴 방정식으로 알려진 일반 고유값 문제이며, 즉 하트리-포크 방정식의 특정 표현이다. MO의 양자 화학 계산을 수행할 수 있는 많은 프로그램이 있다 (예: Spartan, HyperChem).[4]

간단한 설명에서는 실험적 분자 궤도 에너지를 원자가 궤도에 대한 자외선 광전자 분광법과 내각 궤도에 대한 X선 광전자 분광법으로 얻을 수 있다고 종종 제시된다. 그러나, 이들 실험은 이온화 에너지 (분자와 1개의 전자를 제거하여 얻는 이온 중 하나 사이의 에너지 차이)를 측정하기 때문에 부정확하다. 이온화 에너지는 쿱만스 정리에 의해 궤도 에너지와 근사적으로 관련된다. 이 두 값이 잘 일치하는 분자가 있는가 하면, 매우 좋지 않은 경우도 있다.

8. 물리적 의미

분자 궤도는 해당 궤도를 점유하는 하나의 전자가 발견될 수 있는 분자 내 영역을 나타낸다. 분자 궤도는 원자 궤도의 결합으로 얻어진다. 분자 궤도는 분자 내 하나 또는 한 쌍의 전자의 에너지나 공간적인 분배, 즉 분자의 전자 배치에 대한 정보를 줄 수 있다. 흔히 분자 궤도는 원자 오비탈의 선형 결합(LCAO-MO method)으로 나타내는데, 이는 지극히 정성적인 방법이지만 상당히 유용하다. LCAO는 분자 궤도 이론을 통해 이해되는 분자 내 간단한 결합 모델을 제공하는데 매우 유용하다. 계산화학의 최신 기법들은 계의 분자 오비탈을 계산하는 것으로부터 시작한다. 분자 오비탈은 핵에 의해 형성된 전기장 내 한 원자의 거동과 다른 전자들의 평균적인 분포를 기술한다. 당연하게도 이는 근사이고, 분자의 전자에 대한 파동 함수의 가장 정확한 설명은 궤도를 갖지 않는다는 것이다.

분자 궤도는 일반적으로 분자 전체에 비편재화되어 표현된다. 또한, 분자가 대칭 요소를 갖는다면, 그것의 비축퇴 분자 궤도는 이들 대칭 중 어느 하나에 대해 대칭이거나 반대칭이다. 즉, 분자 궤도 ψ에 대칭 연산 S (예를 들어, 반사, 회전 또는 반전)를 적용하면 분자 궤도가 변경되지 않거나 부호가 역전된다.: Sψ = ± ψ. 예를 들어, 평면 분자에서, 분자 궤도는 분자 평면에서 반사와 관련하여 대칭 (σ) 또는 반대칭 (π) 중 하나이다. 축퇴된 궤도 에너지를 가진 분자들도 고려한다면, 분자 궤도가 분자 대칭군의 기약 표현에 대한 기초를 형성한다는 보다 일반적인 진술이 성립한다.[4] 분자 오비탈의 대칭성은 비편재화가 분자 궤도 이론의 고유한 특징이며, 결합을 편재화된 전자쌍으로 보는 원자가 결합 이론과 근본적으로 다르고 상호 보완적임을 의미한다.

만약 분자 궤도가 정규화되어 있다면, 그 절댓값의 제곱에 미소 체적 d\boldsymbol{r}을 곱한 값은:



\phi_i^{*}(\boldsymbol{r})\phi_i(\boldsymbol{r})\,d\boldsymbol{r}

=|\phi_i(\boldsymbol{r})|^2\,d\boldsymbol{r}



은 그 미소 체적 d\boldsymbol{r} 내에서 전자를 발견할 확률을 나타낸다.

9. 응용

분자 궤도(MO)는 전자가 발견될 가능성이 높은 분자 내 영역을 나타낸다. 분자 궤도는 원자 내 전자의 위치를 예측하는 원자 궤도의 결합을 통해 얻어진다. 분자 궤도는 분자의 전자 배치(1개의 전자, 또는 전자 쌍의 공간적 분포 및 에너지)를 상세하게 설명할 수 있다. 일반적으로, 특히 정성적 또는 매우 근사적인 이용에서는 MO는 원자 궤도 함수의 선형 결합으로 표시된다. 이것들은 분자 내 결합에 대한 간단한 모델을 제공하는 데 매우 유용하다. 계산 화학에서 대부분의 현대적인 방법은 계의 MO를 계산하는 것에서 시작한다. 분자 궤도는 원자핵과 다른 전자의 평균 분포에 의해 생성된 전장 내의 1개의 전자의 거동을 설명한다. 2개의 전자가 동일한 궤도를 점유하는 경우, 파울리 배타 원리는 그들이 반대 스핀을 가질 것을 요구한다. 이는 필연적으로 근사이며, 분자의 전자 파동 함수의 정밀한 묘사는 궤도를 갖지 않는다(배치간 상호작용 참조).

화학 반응의 이론적 예측과 그 해석에는 프론티어 궤도 이론이 사용된다.

참조

[1] 서적 orbital https://www.merriam-[...] Merriam-Webster 2021-04-18
[2] 서적 Chemistry : the central science Prentice Hall
[3] 논문 Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations 1932-07
[4] 서적 Chemical applications of group theory https://archive.org/[...] Wiley 1990
[5] 서적 Orbital Interactions in Chemistry Wiley
[6] 논문 Zur Deutung einiger Erscheinungen in den Molekelspektren Springer Science and Business Media LLC
[7] 논문 Zur Deutung der Molekelspektren
[8] 논문 Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities American Physical Society (APS) 1927-05-01
[9] 논문 The assignment of quantum numbers for electrons in molecules. Extracts from Phys. Rev. 32, 186-222 (1928), plus currently written annotations Wiley
[10] 간행물 Friedrich Hund and Chemistry
[11] 간행물 Robert S. Mulliken's Nobel Lecture http://nobelprize.or[...]
[12] 논문 The electronic structure of some diatomic molecules https://www.chemteam[...] 1929
[13] 서적 Inorganic Chemistry https://books.google[...] Pearson Education
[14] 서적 Inorganic Chemistry Pearson Prentice Hall
[15] 서적 Atkins’ Physical Chemistry Oxford University Press
[16] 서적 An Introduction to Molecular Orbitals Oxford University Press
[17] 서적 Principles of Chemistry Norton & Company
[18] 서적 Inorganic chemistry W.H. Freeman 2006
[19] 서적 IUPAC Compendium of Chemical Terminology
[20] 웹사이트 5.3.3: Ionic Compounds and Molecular Orbitals https://chem.librete[...] 2020-08-06
[21] 논문 Electronic structure and bonding of Be2
[22] 논문 Chemical Bonding. VonM. J. Winter. 90 S., ISBN 0-19-855694-2. – Organometallics 1. Complexes with Transition Metal-Carbon σ-Bonds. VonM. Bochmann. 91 S., ISBN 0-19-855751-5. – Organometallics 2. Complexes with Transition Metal-Carbon π-Bonds. VonM. Bochmann. 89 S., ISBN 0-19-855813-9. – Bifunctional Compounds. VonR. S. Ward. 90 S., ISBN 0-19-855808-2. – Alle aus der Reihe: Oxford Chemistry Primers, Oxford University Press, Oxford, 1994, Broschur, je 4.99 £ https://onlinelibrar[...] 1995-02-21
[23] 서적 Inorganic Chemistry Pearson Prentice Hall
[24] 논문 Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations 1932-07
[25] 논문 Zur Deutung einiger Erscheinungen in den Molekelspektren [On the interpretation of some phenomena in molecular spectra]
[26] 논문 Zur Deutung der Molekelspektren. I
[27] 논문 Zur Deutung der Molekelspektren. II
[28] 논문 Zur Deutung der Molekelspektren. III. Bemerkungen über das Schwingungs- und Rotationsspektrum bei Molekeln mit mehr als zwei Kernen
[29] 논문 Zur Deutung der Molekelspektren. IV
[30] 논문 Zur Deutung der Molekelspektren V. Die angeregten Elektronenterme von Molekeln mit zwei gleichen Kernen (H2, He2, Li2, N2+, N2 ...)
[31] 논문 Electronic States and Band Spectrum Structure in Diatomic Molecules. IV. Hund's Theory; Second Positive Nitrogen and Swan Bands; Alternating Intensities
[32] 논문 The assignment of quantum numbers for electrons in molecules. I
[33] 논문 Friedrich Hund and Chemistry
[34] 논문 Spectroscopy, Molecular Orbitals, and Chemical Bonding http://www.nobelpriz[...]
[35] 논문 The electronic structure of some diatomic molecules
[36] 서적 Inorganic Chemistry Pearson Prentice Hall
[37] 서적 Inorganic Chemistry Pearson Prentice Hall
[38] 서적 Atkins’ Physical Chemistry Oxford University Press
[39] 서적 An Introduction to Molecular Orbitals Oxford University Press
[40] 서적 Principles of Chemistry Norton & Company
[41] 논문 Quantum chemical calculations show that the uranium molecule U2 has a quintuple bond http://archive-ouver[...]
[42] 서적 Inorganic Chemistry Pearson Prentice Hall
[43] 저널 Electronic Structures of Polyatomic Molecules and Valence. II. General Considerations https://archive.org/[...] 1932-07
[44] 서적 Chemical applications of group theory https://www.worldcat[...] Wiley 1990
[45] 서적 옥스토비의 일반화학 제 6판
[46] 서적 Inorganic Chemistry: Principles of Structure and Reactivity
[47] 간행물 Robert S. Mulliken's Nobel Lecture


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com