십칠각형

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
- 2.1. 정십칠각형의 작도 가능성 발견
- 2.2. 작도 방법의 발전
3. 정십칠각형의 성질
- 3.1. 기하학적 성질
- 3.2. 대칭성
4. 정십칠각형의 작도
5. 삼각함수 값
6. 관련 다각형
- 6.1. 십칠각성 (Heptadecagram)
- 6.2. 피트리 다각형 (Petrie polygon)
참조

1. 개요

십칠각형은 17개의 변과 꼭짓점을 가진 다각형으로, 정십칠각형은 모든 변의 길이가 같고 내각의 크기가 같은 다각형이다. 1796년 카를 프리드리히 가우스는 자와 컴퍼스만을 사용하여 정십칠각형을 작도할 수 있음을 증명하여, 2000년 이상 정다각형 작도에 있어 진전을 이루었다. 정십칠각형은 이면각 대칭(Dih17)을 가지며, 내각의 합은 2700도, 한 내각의 크기는 약 158.82도이다. 정십칠각형의 작도 방법은 여러 가지가 있으며, 칼라일 원을 이용한 작도법, 요하네스 엘칭거의 64단계 작도법 등이 있다. 또한 십칠각성이라는 별 다각형 형태도 존재한다.

더 읽어볼만한 페이지

카를 프리드리히 가우스 - 가우스 법칙
가우스 법칙은 전기장과 전하 분포의 관계를 나타내는 전자기학의 기본 법칙으로, 폐곡면을 통과하는 전기장의 플럭스는 그 곡면 내부의 알짜 전하량에 비례하며, 맥스웰 방정식의 일부로 고전 전자기학의 기초를 이룬다.
카를 프리드리히 가우스 - 가우스 곡률
가우스 곡률은 3차원 유클리드 공간에 놓인 곡면의 두 주곡률의 곱으로, 곡면의 형태를 나타내는 지표이며 곡면 자체의 길이 측정만으로 결정되는 내재적인 값이다.
작도가능한 다각형 - 정삼각형
정삼각형은 세 변의 길이가 같고 모든 내각이 60°인 삼각형으로, 이등변삼각형의 특수한 형태이며 내심, 외심, 무게중심이 일치하는 특징을 가진다.
작도가능한 다각형 - 오각형
다섯 변으로 이루어진 다각형인 오각형은 변의 길이와 각의 크기가 모두 같은 정오각형을 포함하며, 정오각형은 컴퍼스와 자로 작도할 수 있고 자연에서도 발견된다.
유클리드 평면기하학 - 피타고라스 정리
피타고라스 정리는 직각삼각형에서 직각변의 제곱의 합이 빗변의 제곱과 같다는 정리로, a² + b² = c²으로 표현되며, 한 변의 길이를 계산하는 데 사용되고, 여러 지역에서 알려졌으나 피타고라스 학파에 의해 체계화되었다고 전해진다.
유클리드 평면기하학 - 스튜어트 정리
스튜어트 정리는 삼각형의 변과 체바 선분 사이의 관계를 나타내는 기하학 정리이며, 아폴로니우스 정리를 포함하고 코사인 법칙을 이용하여 증명한다.

십칠각형
개요
칠십각형
종류	정다각형
변의 수	17
꼭짓점의 수	17
슈플리 기호	'{17}'
각도
내각의 크기	158.82352941도
중심각의 크기	21.17647058도
작도
작도 가능 여부	자와 컴퍼스로 작도 가능
성질
넓이	'a² cot ≈ 22.73549192 a²}} (a는 변의 길이)'
내부 각의 합	2700도

2. 역사

1796년, 19세의 카를 프리드리히 가우스는 눈금 없는 자와 컴퍼스만으로 정십칠각형을 작도할 수 있다는 것을 증명했다.^[1] 이는 정다각형 작도 문제에서 약 2000년 만의 중대한 진전이었다.^[1] 가우스는 정다각형의 작도가 가능하려면 공통 각의 삼각 함수를 산술 연산과 제곱근 추출을 사용하여 표현할 수 있어야 하고, 정다각형 변의 수( $N$ )의 홀수 소인수가 서로 다른 페르마 소수( $F_n = 2^{2^n} + 1$ 형태)여야 한다는 사실을 이용했다.

가우스는 저서 《산술 탐구》에서^[2] $2\pi/17$ 의 코사인 값을 아래와 같이 제곱근으로 표현했다.^[3]

: $\begin{align}\cos\frac{2\pi}{17} = & \frac{1}{16}\left(\sqrt{17}-1+\sqrt{34-2\sqrt{17}}\right)\\& + \frac{1}{8}\left(\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}} \right).\\\end{align}$

2. 1. 정십칠각형의 작도 가능성 발견

1796년, 19세의 카를 프리드리히 가우스는 정십칠각형이 눈금 없는 자와 컴퍼스를 사용하여 작도 가능하다는 것을 증명했다.^[1] 이는 정다각형 작도 문제에 있어 2000년 만의 중대한 진전이었다.^[1] 가우스의 증명은 정다각형의 작도가 가능하려면 공통 각의 삼각 함수를 산술 연산과 제곱근 추출을 사용하여 표현할 수 있어야 하고, 정다각형 변의 수(

N

)의 홀수 소인수가 서로 다른 페르마 소수(

F_n = 2^{2^n} + 1

형태)여야 한다는 두 가지 사실에 기반한다.

가우스는 자신의 저서 《산술 탐구》(Disquisitiones Arithmeticae)^[2]에서

2\pi/17

의 코사인 값을 제곱근으로 표현하면 다음과 같다고 제시했다.^[3]

:

\begin{align}\cos\frac{2\pi}{17} = & \frac{1}{16}\left(\sqrt{17}-1+\sqrt{34-2\sqrt{17}}\right)\\& + \frac{1}{8}\left(\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}} \right).\\\end{align}

2. 2. 작도 방법의 발전

1796년, 19세의 카를 프리드리히 가우스는 정십칠각형이 눈금 없는 자와 컴퍼스만으로 작도 가능하다는 것을 증명했다.^[1] 이는 2000년 이상 정다각형 작도에 있어서 최초의 진전이었다.^[1] 가우스의 증명은 정다각형의 변의 수가 서로 다른 페르마 소수의 곱과 2의 거듭제곱의 곱으로 표현될 수 있을 때 작도가 가능하다는 사실에 기반한다. 정십칠각형의 경우, 17이 페르마 소수이므로 작도가 가능하다. 가우스는 자신의 저서 《산술 탐구》에서^[2] 정십칠각형의 작도 가능성을

2\pi/17

의 코사인 값을 제곱근을 사용하여 표현함으로써 보였다.^[3]

정삼각형, 오각형, 십오각형과 같이 변의 수가 2의 거듭제곱인 정다각형의 작도는 유클리드에 의해 알려졌지만, 3과 5 이외의 페르마 소수를 기반으로 하는 정다각형(정십칠각형, 정257각형, 정65537각형 등)의 작도는 고대에는 알려지지 않았다.

이후 정십칠각형의 구체적인 작도 방법들이 제시되었다. 1893년 허버트 윌리엄 리치먼드는 칼라일 원을 이용한 정십칠각형 작도법을 발표했다.^[6]

요하네스 엘칭거^영어는 1800년경에 64단계로 이루어진 작도법을 발견했다.^[12]

center

3. 정십칠각형의 성질

정십칠각형의 중심각과 외각은 약 21.18°이며, 내각은 약 158.82°이다.

3. 1. 기하학적 성질

정십칠각형의 중심각과 외각은 약 21.18°이며, 내각은 약 158.82°이다. 또한, 한 변의 길이가

a

인 정십칠각형의 면적은

{17a^2\over4}\cot{\pi\over{17}}\approx22.7354919a^2

이다.

3. 2. 대칭성

정십칠각형의 대칭. 꼭짓점은 대칭 위치에 따라 색상이 지정되어 있으며, 파란색 거울 선은 꼭짓점과 모서리를 통과하여 그려져 있다. 회전 차수는 중앙에 표시되어 있다.

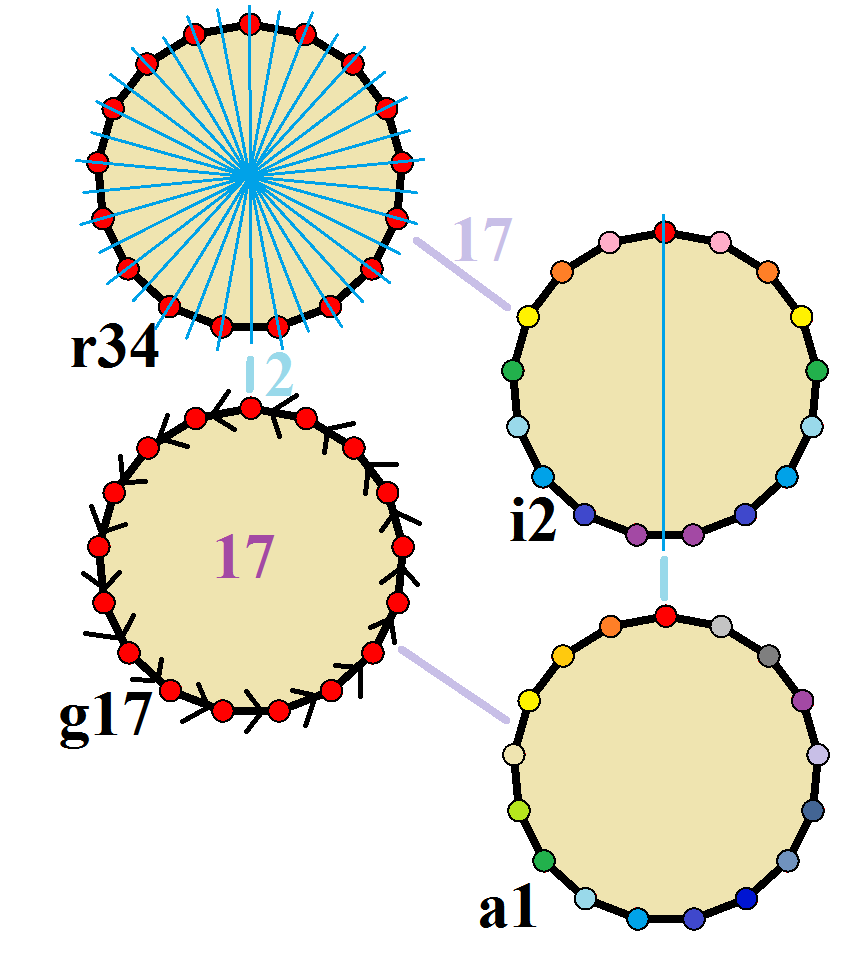
정십칠각형은 Dih₁₇ 대칭이며, 차수는 34이다. 17은 소수이므로 이면각 대칭을 갖는 하위 그룹은 Dih₁이고, 순환군 대칭은 Z₁₇ 및 Z₁이다.

이 4개의 대칭은 십칠각형에서 4개의 다른 대칭으로 볼 수 있다. 존 콘웨이는 이를 문자와 그룹 차수로 표시한다.^[7] 정규 형태의 전체 대칭은 '''r34'''이고, 대칭이 없는 것은 '''a1'''로 표시된다. 이면각 대칭은 꼭짓점을 통과하는지(대각선에 대한 '''d''') 또는 모서리를 통과하는지(수직에 대한 '''p''')에 따라 나뉘며, 반사선이 모서리와 꼭짓점 모두를 통과할 때는 '''i'''로 표시된다. 중앙 열의 순환 대칭은 중심 회전 차수에 따라 '''g'''로 표시된다.

각 하위 그룹 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. '''g17''' 하위 그룹만이 자유도가 없지만 방향성 모서리로 볼 수 있다.

4. 정십칠각형의 작도

C. F. 가우스의 ''Intelligenzblatt der allgemeinen Literatur-Zeitung'' 게재물

17은 페르마 소수이므로 정십칠각형은 작도 가능한 다각형이다. 즉, 눈금 없는 자와 컴퍼스를 사용하여 작도할 수 있다. 이는 1796년 19세의 카를 프리드리히 가우스(Carl Friedrich Gauss)가 증명했으며,^[1] 2000년 이상 정다각형 작도에 있어서 최초의 진전이었다.^[1]

가우스의 증명은 정다각형의 변의 수

N

의 홀수 소인수가 서로 다른 페르마 소수, 즉

F_n = 2^{2^n} + 1

의 형태를 갖는 경우에 작도가 가능하다는 사실에 기반한다. 정십칠각형을 작도하는 것은

2\pi/17

의 코사인을 제곱근으로 표현하는 것을 포함한다. 가우스의 저서 ''산술 탐구(Disquisitiones Arithmeticae)''^[2]는 이를 (현대 표기법으로) 다음과 같이 제시한다.^[3]

:

\begin{align}\cos\frac{2\pi}{17} = & \frac{1}{16}\left(\sqrt{17}-1+\sqrt{34-2\sqrt{17}}\right)\\& + \frac{1}{8}\left(\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}} \right).\\\end{align}

정삼각형, 정오각형, 정십오각형처럼 변의 수가 ''2''^''h''배인 다각형에 대한 작도는 유클리드에 의해 주어졌지만, 3과 5 이외의 페르마 소수에 기초한 작도는 고대에는 알려지지 않았다. 알려진 유일한 페르마 소수는 ''F_n'' for ''n'' = 0, 1, 2, 3, 4 (3, 5, 17, 257, 65537)이다.

정십칠각형의 구체적인 작도는 1893년 허버트 윌리엄 리치먼드(Herbert William Richmond)에 의해 제시되었다.

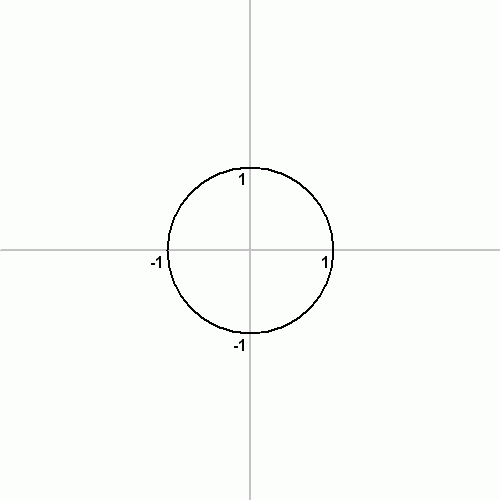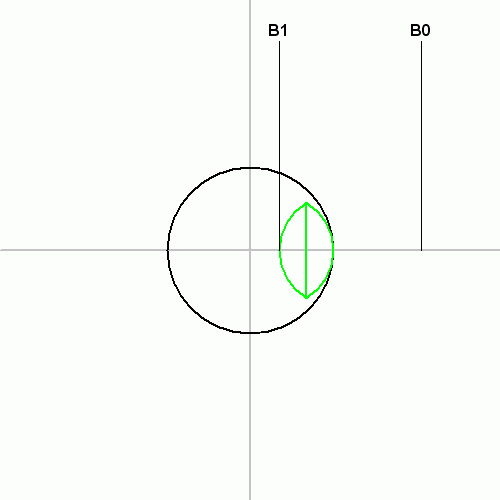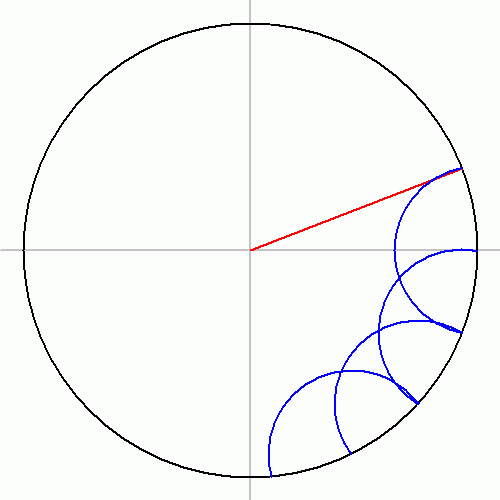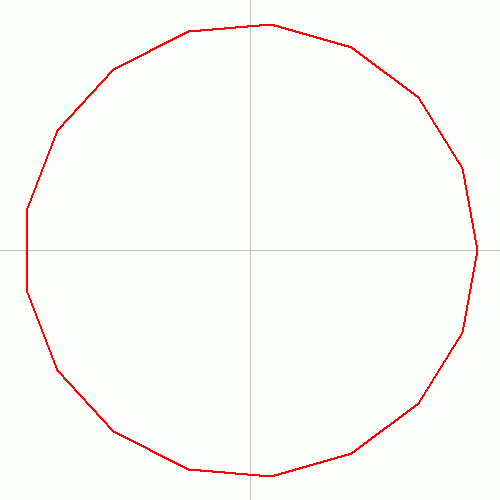
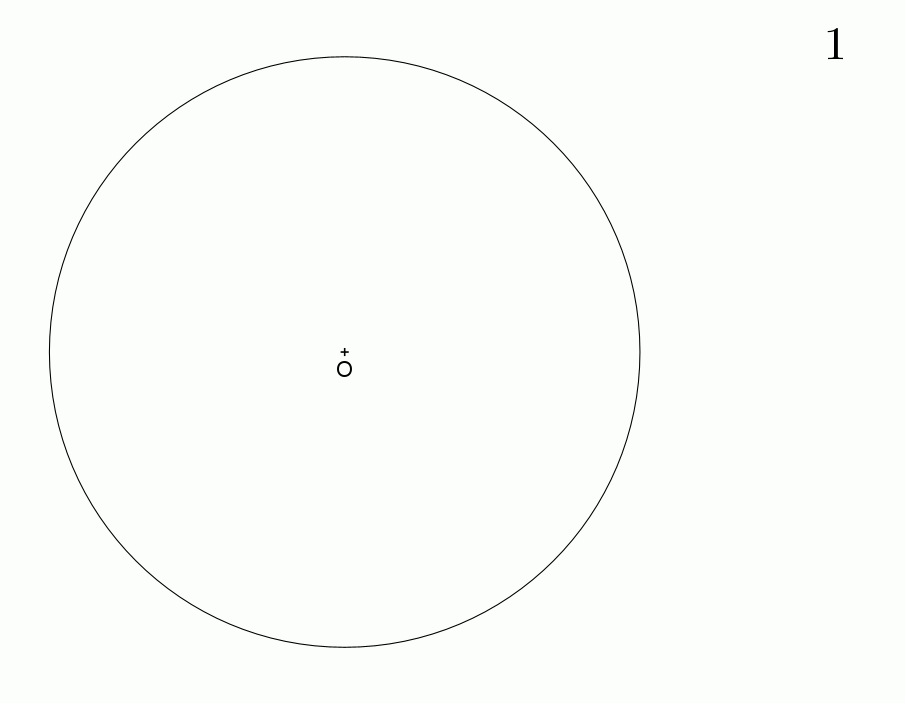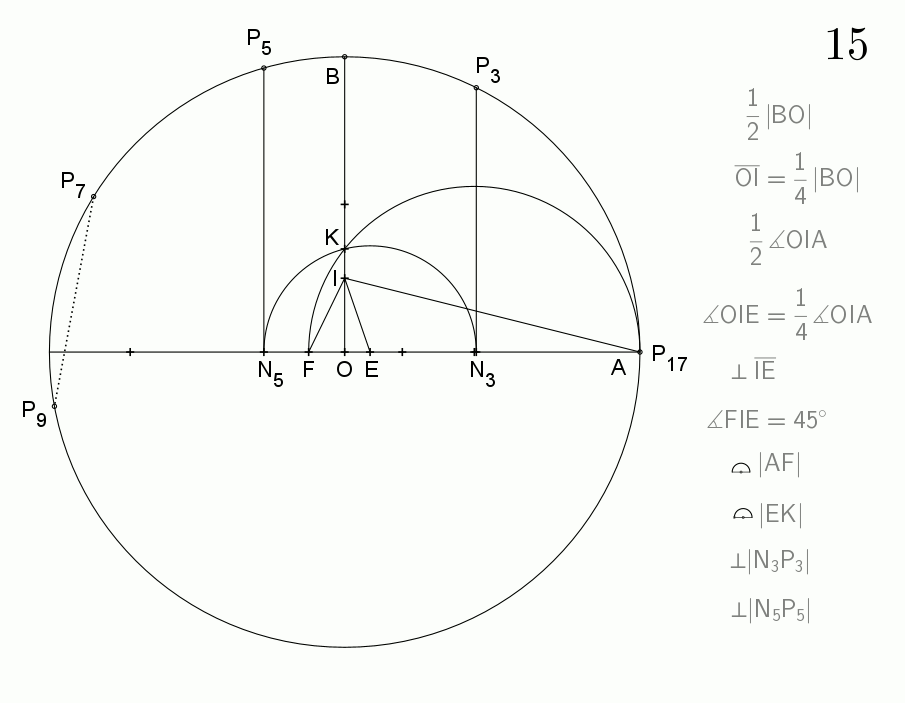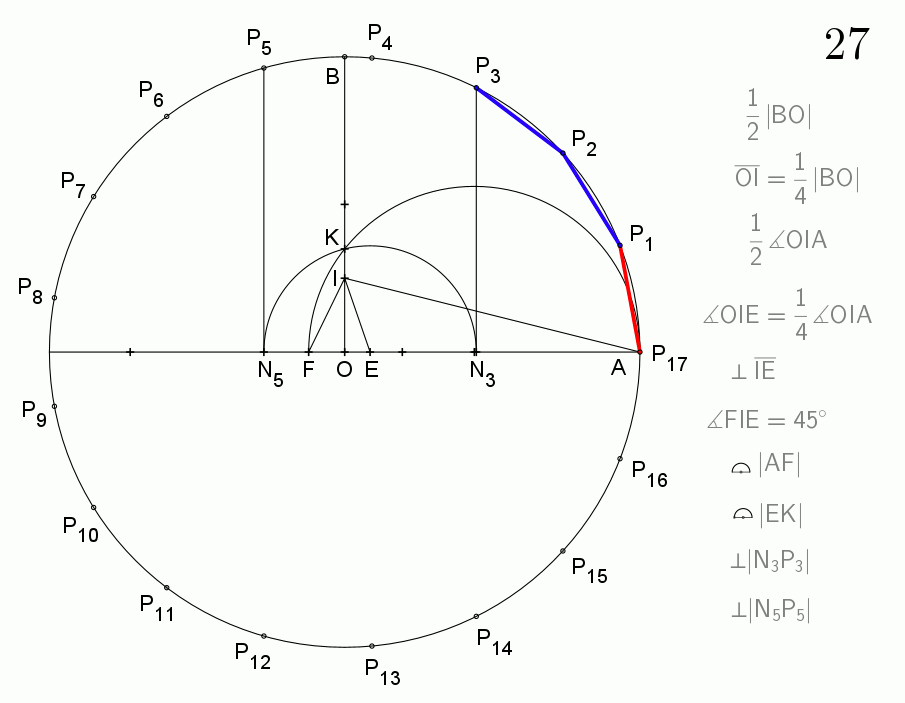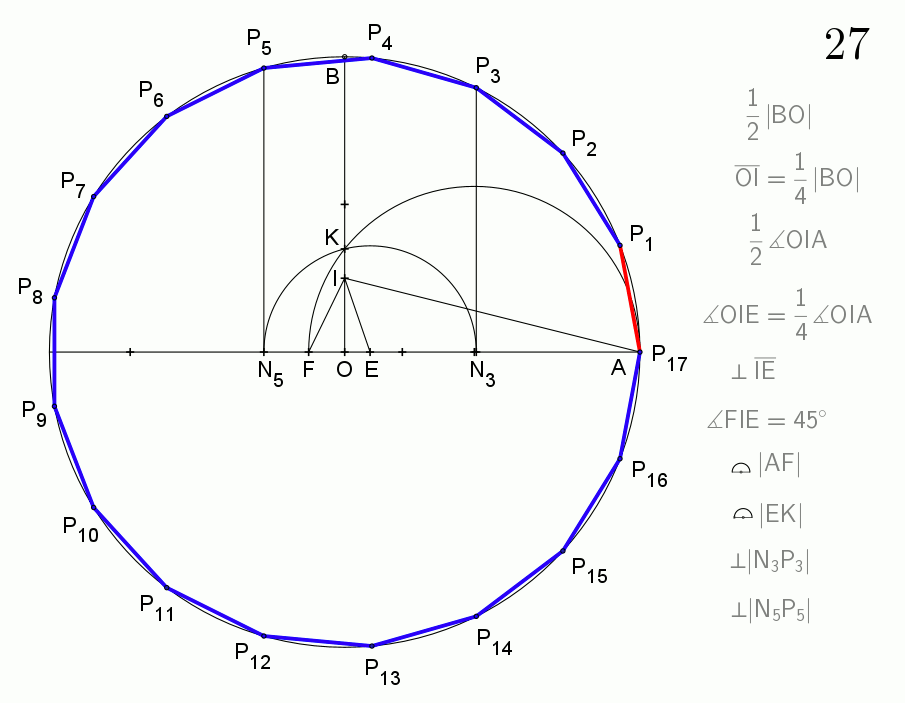
4. 1. 칼라일 원을 이용한 작도

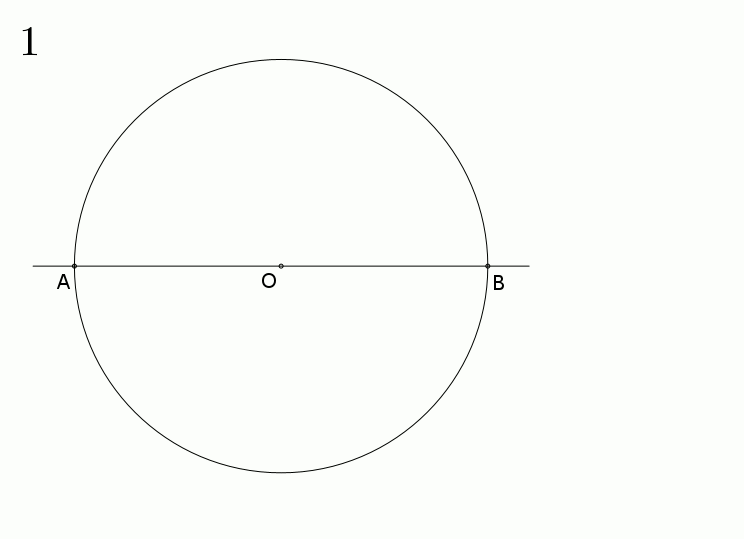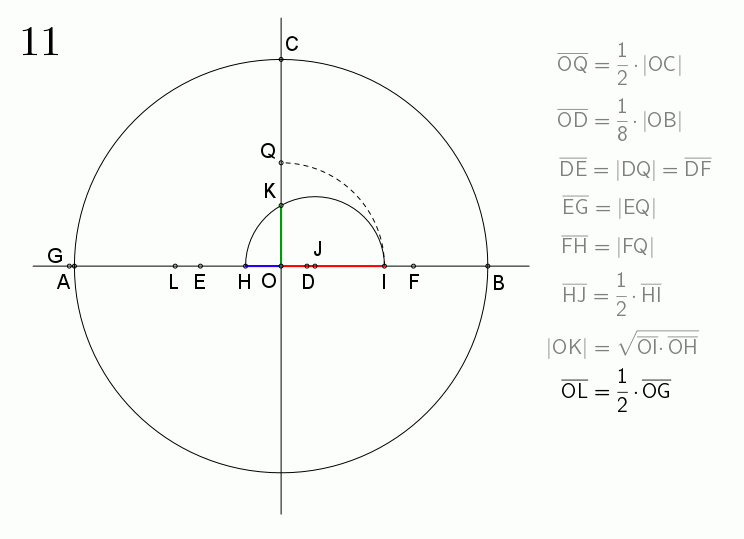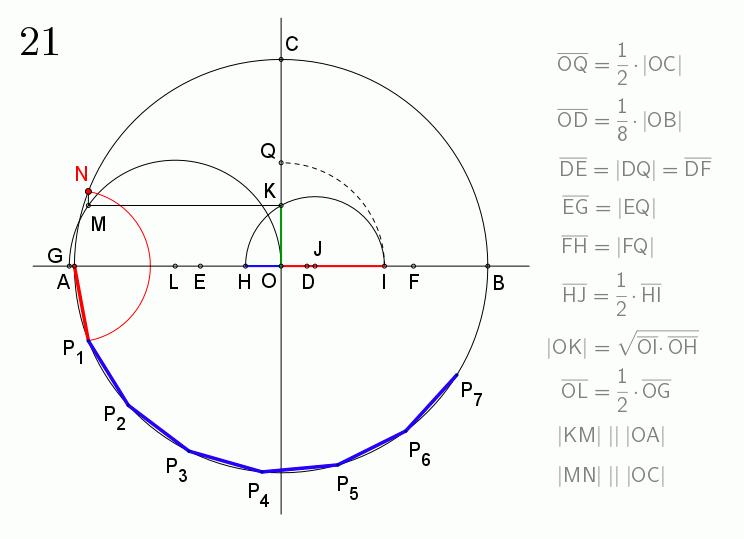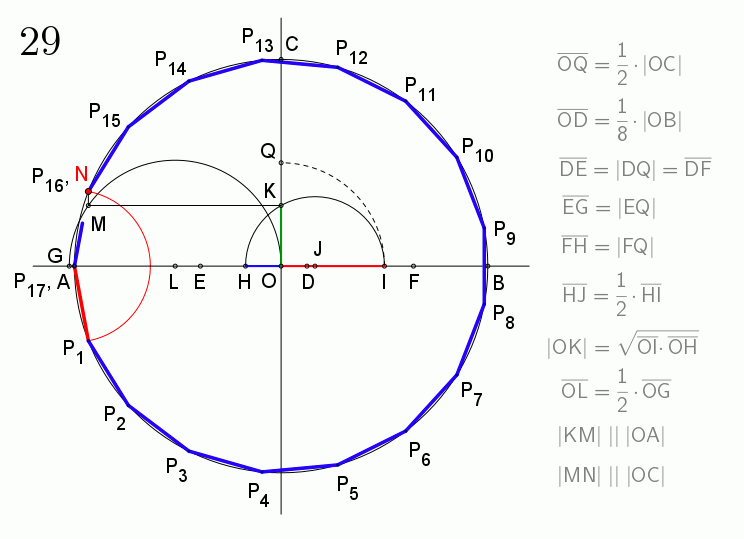
허버트 윌리엄 리치먼드는 칼라일 원을 이용하여 정십칠각형을 작도하는 방법을 제시했다.^[6] 그 방법은 다음과 같다.

1. 원의 서로 수직인 두 반지름 OA, OB를 그린다.

2. OI를 OB의 4분의 1 크기로 만든다.

3. 각 OIE를 각 OIA의 4분의 1이 되도록 만든다.

4. OA의 연장선에서 각 EIF가 45°가 되도록 점 F를 찾는다.

5. AF를 지름으로 하는 원을 그려 OB와 점 K에서 만나도록 한다.

6. 중심이 E이고 반지름이 EK인 원을 그려 OA와 N₃, N₅에서 만나도록 한다.

7. N₃P₃, N₅P₅를 수선으로 원에 그리면, 호 AP₃, AP₅는 각각 원주의 17분의 3과 17분의 5가 된다.

N₃은 AF에 대한 탈레스의 정리의 중심점과 매우 가깝다.

H. W. 리치먼드의 작도를 변형한 방법은 다음과 같다.

원 k₂는 이등분선 w₃ 대신 점 H를 결정한다.
점 G'(m에서 점 G를 반사)를 중심으로 하는 원 k₄는 접선 작도를 위해 M에 더 가깝지 않은 점 N을 만든다.
일부 명칭이 변경되었다.

4. 2. 요하네스 엘칭거의 작도

요하네스 엘칭거^영어에 의해 1800년경에 발견된 정17각형의 구체적인 작도 방법은 다음과 같다.^[12] 총 64단계로 구성되어 있으며, 눈금 없는 자와 컴퍼스만을 사용하여 정십칠각형을 그릴 수 있다.

다음은 작도의 절차를 설명한다(괄호 안은 애니메이션에서의 단계 번호).

1. 를 중심으로 하는 원주 위에 점 , 가 있고, 와 는 직교하는 것으로 한다(1-5).

2. 선분 위에 점 를 = 가 되도록 한다(6-10).

3. 선분 위에 점 를 = 가 되도록 한다(11-18).

4. 의 연장선 위에 점 를 = 45°}}가 되도록 한다(19-24).

5. 를 지름으로 하는 원과 의 교점을 로 한다(25-28).

6. 를 반지름으로 하는 원과 선분 의 교점을 로 한다(29).

7. 를 지나, 에 직교하는 직선과 원 의 교점을 로 한다(30-33).

8. 점 는 점 에서 세어 정십칠각형의 3번째 꼭짓점이므로, 컴퍼스의 폭을 로 하여 모든 꼭짓점을 얻을 수 있다(34-47).

9. 마지막으로 꼭짓점을 모두 연결하면 정십칠각형을 얻는다(48-64).

4. 3. 기타 작도법

T. P. 스토웰은 1877년 ''The Analyst''에 원의 지름과 수직인 반지름을 그리고, 반지름의 절반 및 8분의 1 지점을 찾아 여러 보조선과 원을 그리는 복잡한 작도법을 게재했다. 이 과정을 통해 최종적으로 원주를 17등분하는 점을 찾는다.^[5]

T. P. 스토웰의 작도 (1818년). OK는 OH와 OQ의 기하 평균이다.

T. P. 스토웰의 작도 (1818년) 애니메이션. OK는 OH와 OQ의 기하 평균이다.

H. W. 리치먼드는 1893년에 더 간단한 작도법을 제시했다.^[6] 원의 수직인 두 반지름을 그리고, 한 반지름의 4분의 1 지점을 찾아 각을 4등분하는 보조선을 긋는다. 이후 여러 보조 원을 그려 원주를 17등분하는 점을 찾는다. 이 방법에서 N₃은 AF에 대한 탈레스의 정리의 중심점과 매우 가깝다.

H. W. 리치먼드의 작도법을 변형한 방법도 존재한다. 이 방법은 원 k₂가 점 H를 결정하고, 점 G' 주변의 원 k₄가 점 N을 생성하는 등 약간의 차이가 있다.

5. 삼각함수 값

정십칠각형의 작도 가능성은 삼각함수 값을 제곱근으로 표현할 수 있다는 것과 같다. 카를 프리드리히 가우스는 그의 저서 ''산술 탐구''에서^[2] (현대 표기법으로) 다음과 같이 $\cos\frac{2\pi}{17}$ 의 값을 제시했다.^[3]

: $\begin{align}\cos\frac{2\pi}{17} = & \frac{1}{16}\left(\sqrt{17}-1+\sqrt{34-2\sqrt{17}}\right)\\& + \frac{1}{8}\left(\sqrt{17+3\sqrt{17}-\sqrt{34-2\sqrt{17}}-2\sqrt{34+2\sqrt{17}}} \right).\\\end{align}$

다른 각도에 대한 삼각함수 값도 복잡한 제곱근 식으로 표현할 수 있다. 예를 들어 m=1인 경우,

: $\cos\frac{\pi}{17} = \frac{\sqrt{34-\sqrt{68}}-\sqrt{17}+1 + 2\sqrt{\sqrt{34-\sqrt{68}}+\sqrt{17}-1} \sqrt{\sqrt{17+\sqrt{272}}}}{16}$

1사분면에서의 Cos와 Sin (m π / 17) 값은 다음과 같다. (다른 사분면은 계산 가능)

1사분면에서의 Cos와 Sin (m π / 17)
m	16 cos (m π / 17)	8 sin (m π / 17)
1	$+1-\sqrt{17}+\sqrt{34-\sqrt{68}} + \sqrt{68+\sqrt{2448}+\sqrt{2720+\sqrt{6284288}}}$	$\sqrt{34 - \sqrt{68} - \sqrt{136-\sqrt{1088}} - \sqrt{272+\sqrt{39168}-\sqrt{43520+\sqrt{1608777728}}}}$
2	$-1+\sqrt{17}+\sqrt{34-\sqrt{68}} + \sqrt{68+\sqrt{2448}-\sqrt{2720+\sqrt{6284288}}}$	$\sqrt{34 - \sqrt{68} + \sqrt{136-\sqrt{1088}} - \sqrt{272+\sqrt{39168}+\sqrt{43520+\sqrt{1608777728}}}}$
3	$+1+\sqrt{17}+\sqrt{34+\sqrt{68}} + \sqrt{68-\sqrt{2448}-\sqrt{2720-\sqrt{6284288}}}$	$\sqrt{34 + \sqrt{68} - \sqrt{136+\sqrt{1088}} - \sqrt{272-\sqrt{39168}+\sqrt{43520-\sqrt{1608777728}}}}$
4	$-1+\sqrt{17}-\sqrt{34-\sqrt{68}} + \sqrt{68+\sqrt{2448}+\sqrt{2720+\sqrt{6284288}}}$	$\sqrt{34 - \sqrt{68} - \sqrt{136-\sqrt{1088}} + \sqrt{272+\sqrt{39168}-\sqrt{43520+\sqrt{1608777728}}}}$
5	$+1+\sqrt{17}+\sqrt{34+\sqrt{68}} - \sqrt{68-\sqrt{2448}-\sqrt{2720-\sqrt{6284288}}}$	$\sqrt{34 + \sqrt{68} - \sqrt{136+\sqrt{1088}} + \sqrt{272-\sqrt{39168}+\sqrt{43520-\sqrt{1608777728}}}}$
6	$-1-\sqrt{17}+\sqrt{34+\sqrt{68}} + \sqrt{68-\sqrt{2448}+\sqrt{2720-\sqrt{6284288}}}$	$\sqrt{34 + \sqrt{68} + \sqrt{136+\sqrt{1088}} - \sqrt{272-\sqrt{39168}-\sqrt{43520-\sqrt{1608777728}}}}$
7	$+1+\sqrt{17}-\sqrt{34+\sqrt{68}} + \sqrt{68-\sqrt{2448}+\sqrt{2720-\sqrt{6284288}}}$	$\sqrt{34 + \sqrt{68} + \sqrt{136+\sqrt{1088}} + \sqrt{272-\sqrt{39168}-\sqrt{43520-\sqrt{1608777728}}}}$
8	$-1+\sqrt{17}+\sqrt{34-\sqrt{68}} - \sqrt{68+\sqrt{2448}-\sqrt{2720+\sqrt{6284288}}}$	$\sqrt{34 - \sqrt{68} + \sqrt{136-\sqrt{1088}} + \sqrt{272+\sqrt{39168}+\sqrt{43520+\sqrt{1608777728}}}}$

6. 관련 다각형

십칠각형과 관련된 다각형으로 십칠각성이 있다. 십칠각성은 17개의 변을 가진 별 다각형이다. 정십칠각형은 16차원 정다면체인 16-단체의 피트리 다각형이기도 하다.

6. 1. 십칠각성 (Heptadecagram)

십칠각성은 17개의 변을 가진 별 다각형이다. 슐래플리 기호로 표현되는 7가지 정규 형태가 있다: {17/2}, {17/3}, {17/4}, {17/5}, {17/6}, {17/7}, {17/8}. 17은 소수이므로, 이들 모두 정규 별이며 복합 도형은 아니다.

그림	내각
{17/2}	≈137.647°
{17/3}	≈116.471°
{17/4}	≈95.2941°
{17/5}	≈74.1176°
{17/6}	≈52.9412°
{17/7}	≈31.7647°
{17/8}	≈10.5882°

6. 2. 피트리 다각형 (Petrie polygon)

정십칠각형은 16차원 정다면체인 16-단체의 피트리 다각형이며, 비스듬한 직교 투영으로 투영된다.

16-단체 (16D)

참조

_[1] 서적 Abstract Algebra and Famous Impossibilities https://books.google[...] Springer 1991
_[2] 서적 Disquisitiones Arithmeticae https://edoc.hu-berl[...] eod books2ebooks
_[3] 간행물 The central angle of the regular 17-gon https://www.cambridg[...] 1983-12
_[4] 간행물 Carlyle Circles and the Lemoine Simplicity of Polygon Constructions https://web.archive.[...] 1991-02
_[5] 간행물 Answer to Mr. Heal's Query; T. P. Stowell of Rochester, N. Y. https://books.google[...] 1877
_[6] 간행물 A Construction for a regular polygon of seventeen side http://gdz.sub.uni-g[...]
_[7] 서적 The Symmetries of Things 2008
_[8] 서적 高木 1995
_[9] 서적 高木 1996
_[10] 서적 高木 1995
_[11] 서적 高木 1996
_[12] 서적 ハーディ＆ライト 2001

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com