앙상블 (물리학)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사
3. 주요 앙상블
4. 앙상블 평균
5. 앙상블의 표현
- 5.1. 고전 역학
- 5.2. 양자 역학
6. 에르고드 가설
7. 리우빌 정리
8. 통계역학의 응용
참조

1. 개요

앙상블은 물리학에서 사용되는 개념으로, 여러 개의 가상적인 시스템 집합을 의미하며, 각 시스템은 동일한 거시적 조건을 갖지만 미시적 상태는 다를 수 있다. 앙상블 개념은 19세기 후반 볼츠만과 기브스에 의해 도입되었으며, 통계역학의 주요 개념으로 자리 잡았다. 주요 앙상블로는 에너지, 부피, 입자 수가 고정된 미시 정준 앙상블, 온도와 입자 수가 고정된 정준 앙상블, 온도와 화학 포텐셜이 고정된 그랜드 정준 앙상블 등이 있다. 앙상블 평균은 시스템의 물리량을 앙상블 내 모든 미시 상태에 대해 가중 평균한 값이며, 에르고드 가설은 시간 평균과 앙상블 평균이 같다는 가설이다. 앙상블 개념은 최대 엔트로피 원리, 이징 모형, 마르코프 랜덤 필드 등 다양한 분야에 응용된다.

2. 역사

루트비히 볼츠만은 기체 분자 운동론을 통해 이상 기체를 다수의 분자 집합체로 보고, 분자들의 충돌과 확률적 운동을 통해 기체의 성질을 설명하려 했다. 그러나 당시에는 분자의 존재가 명확히 증명되지 않아 비판을 받았다.

1878년 조시아 윌러드 기브스는 통계 앙상블 개념을 도입하여, 역학계 전체의 상태가 확률적으로 나타난다고 보았다.^[13] 이는 분자의 존재를 가정하지 않고도 통계역학을 설명할 수 있는 기반을 마련했으며, 현재 통계역학의 주류 이론으로 자리 잡았다.

3. 주요 앙상블

앙상블은 거시적 제약 조건에 따라 여러 종류로 나뉜다. 대표적인 앙상블은 다음과 같다.

미소 정준 앙상블: 전체 에너지가 일정한 계의 앙상블이다.
정준 앙상블: 온도가 일정한 계의 앙상블이다.
대정준 앙상블: 온도와 화학 퍼텐셜이 일정한 계의 앙상블이다.
등온-등압 앙상블: 온도와 압력이 일정한 앙상블이다.

조시아 윌러드 기브스는 서로 다른 거시적 제약 조건들이 특정한 통계적 특성을 가진 서로 다른 유형의 앙상블로 이어진다고 언급했다.^[5]

루트비히 볼츠만 등의 기체 분자 운동론에서는 이상 기체를 다수의 분자 집합체로 보고, 분자 충돌로 인한 개별 분자의 역학적 상태가 확률적으로 나타나는 것으로 간주했다(분자적 혼돈). 그러나 당시 분자 존재가 확증되지 않아 비판받았다. 반면, 1878년 조시아 윌러드 기브스가 도입한 통계 앙상블은 역학계 전체의 역학적 상태가 확률적으로 나타나는 것으로 간주한다.^[13] 이 관점에서는 분자 존재를 가정할 필요가 없으며, 오늘날 통계 역학의 주류가 되었다.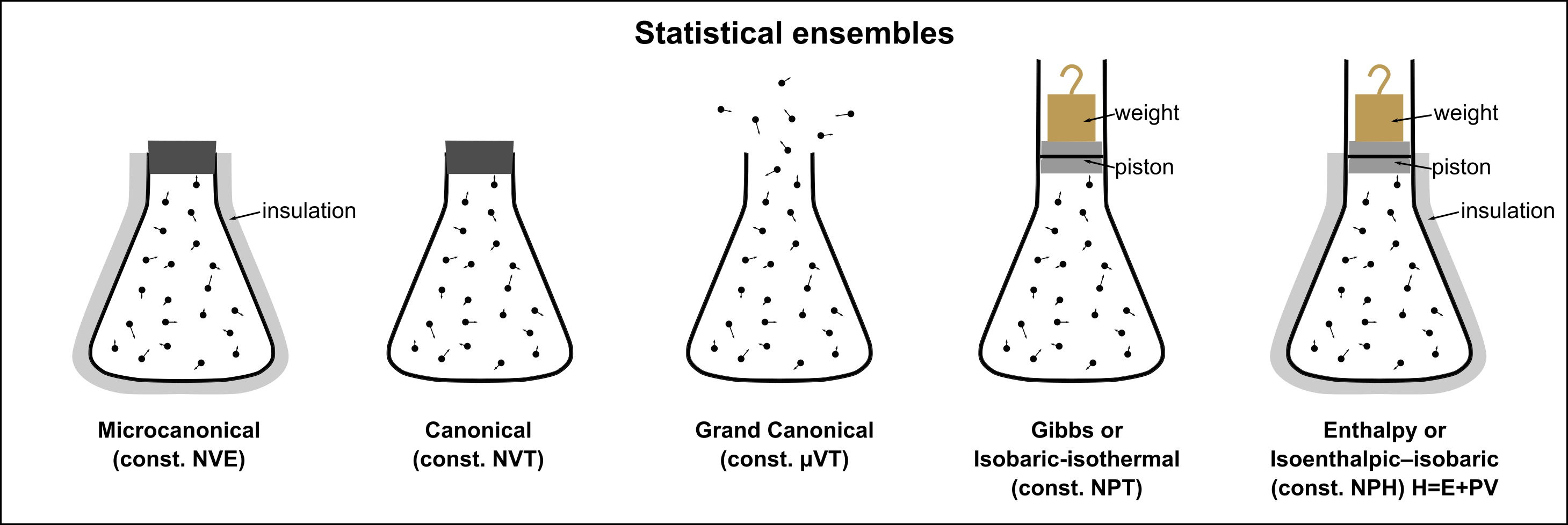

다섯 개의 통계적 앙상블을 시각적으로 표현 (왼쪽에서 오른쪽으로): 미시 정준 앙상블, 정준 앙상블, 그랜드 정준 앙상블, 등압-등온 앙상블, 등엔탈피-등압 앙상블

3. 1. 미소 정준 앙상블 (Microcanonical Ensemble, NVE 앙상블)

미시 정준 앙상블(microcanonical ensemble, NVE 앙상블)은 에너지(''E''), 부피(''V''), 입자 수(''N'')가 모두 일정한 고립계를 나타낸다. 계가 가질 수 있는 모든 미시적 상태는 동일한 확률로 나타나는데(등확률의 원리), 이를 수식으로 표현하면 다음과 같다.^[15]

:

여기서 는 미시적 상태 가 나타날 확률, 는 계가 취할 수 있는 미시적 상태의 총 개수이다.

볼츠만에 따르면, 엔트로피 ''S''는 다음과 같이 가능한 미시 상태의 수 ''W''와 관련된다.^[16] (볼츠만 원리)

:

3. 2. 정준 앙상블 (Canonical Ensemble, NVT 앙상블)

정준 앙상블(canonical ensemble, NVT 앙상블)은 주변 환경(일반적으로 열원)과 에너지를 교환할 수 있지만 부피(''V'')와 입자 수(''N'')는 모두 일정한 닫힌계를 나타낸다.^[14] 거대한 열욕과 에너지 교환이 가능한 계의 앙상블로, 열욕의 열용량은 충분히 크고, 계의 온도는 일정하다고 가정할 수 있다. 이는 폐쇄계에 해당한다.

이 앙상블에서 미시적 상태 ω가 나타날 확률 p(ω)는

:

p(\omega) = \frac{1}{Z} e^{-\beta E(\omega)}

로 주어진다.^[17] 여기서, β는 역온도, E(ω)는 미시적 상태 ω의 에너지이다. Z는

:

Z =\sum_{\omega}  e^{-\beta E(\omega)}

로 정의되는 분배 함수^[18]라고 불리는 양이다. Z는 헬름홀츠 자유 에너지 F와

:

F=-\frac{1}{\beta}\ln Z

의 관계에 있다.^[19]

정준 앙상블은 에너지가 정확히 알려져 있지 않지만 입자 수는 고정된 통계적 앙상블이다. 에너지 대신에 온도가 지정된다. 정준 앙상블은 약한 열적 접촉 상태이거나 열욕조와 약한 열적 접촉을 했던 닫힌 시스템을 설명하는 데 적합하다. 통계적 평형 상태가 되려면 시스템이 완전히 닫혀 있어야 하며 (환경과 입자를 교환할 수 없음) 동일한 온도를 가진 앙상블로 설명되는 다른 시스템과 약한 열적 접촉을 할 수 있다.^[2]

3. 3. 대정준 앙상블 (Grand Canonical Ensemble, μVT 앙상블)

대정준 앙상블(Grand Canonical Ensemble, μVT 앙상블)은 열린계를 나타내는 앙상블로, 온도(T), 부피(V), 화학 퍼텐셜(μ)이 고정되어 있다. 계는 열 저장고 및 입자 저장고와 에너지 및 입자 교환을 통해 열역학적 평형을 이룬다.^[2] 각 미시 상태의 확률은 에너지와 입자 수에 의존하는 인자에 비례한다. 그랜드 포텐셜(J)은 대분배 함수(Ξ)와 관련된 공식 (

J=-\frac{1}{\beta}\ln \Xi

)으로 주어진다.^[21]

대정준 앙상블에서 미시적 상태 ω가 나타날 확률 는

:

p(\omega) = \frac{1}{\Xi} e^{-\beta \left(E(\omega)- \mu N(\omega)\right)}

:로 주어진다.^[20] 여기서, β는 역온도, μ는 화학 퍼텐셜, , 는 미시적 상태 ω의 에너지와 입자 수이다. Ξ는

:

\Xi = \sum_\omega e^{-\beta \left( E(\omega)-\mu N(\omega)\right) }

:로 정의되는 대분배 함수이다.^[20]

3. 4. 등온-등압 앙상블 (Isothermal-Isobaric Ensemble, NPT 앙상블)

온도, 압력, 입자 수(N)가 일정한 앙상블이다.

4. 앙상블 평균

앙상블 평균은 시스템의 물리량(관측량)을 앙상블 내의 모든 미시 상태에 대해 가중 평균한 값이다. 선택된 통계적 앙상블에 따라 앙상블 평균의 수학적 표현은 달라진다. 그러나 주어진 물리량에 대해 얻어진 평균은 열역학적 극한에서 선택된 앙상블에 의존하지 않는다.

열적 평형 상태에 있는 고전적 시스템의 경우, ''앙상블 평균''은 시스템의 위상 공간에 대한 적분 형태로 나타난다.

: $\bar{A} = \frac{\int{Ae^{-\beta H(q_1, q_2, \dots, q_M, p_1, p_2, \dots, p_N)} \,d\tau}}}{\int{e^{-\beta H(q_1, q_2, \dots, q_M, p_1, p_2, \dots, p_N)} \,d\tau}}}$

여기서

$\bar{A}$ 는 시스템 속성 ''A''의 앙상블 평균이다.
$\beta$ 는 $\frac{1}{kT}$ 이며, 열역학적 베타라고 알려져 있다.
''H''는 좌표 집합 $q_i$ 와 짝을 이루는 일반화된 운동량 $p_i$ 의 관점에서 고전적 시스템의 해밀턴이다.
$d\tau$ 는 관심 있는 고전적 위상 공간의 부피 요소이다.

이 식의 분모는 분배 함수라고 하며 문자 ''Z''로 표시된다.

양자 계가 환경과 열적 평형 상태에 있는 경우, 양자 통계 역학에서 가중 평균은 연속 적분이 아닌 양자 에너지 상태의 합 형태로 나타난다.

:

\bar{A} = \frac{\sum_i A_ie^{-\beta E_i}}{\sum_i e^{-\beta E_i}}.

5. 앙상블의 표현

통계적 앙상블은 고려 중인 역학의 유형(양자 또는 고전)에 따라 다른 수학적 표현을 갖는다. 고전적인 경우 앙상블은 미시 상태에 대한 확률 분포이며, 폰 노이만에 의한 양자 역학에서는 각 가환 관측 가능량의 완전 집합의 결과에 확률 분포를 할당하는 방법이다. 고전 역학에서 앙상블은 위상 공간에서 확률 분포로 작성되며, 미시 상태는 위상 공간을 동일한 크기의 단위로 분할한 결과이지만, 이러한 단위의 크기는 다소 임의로 선택할 수 있다.

5. 1. 고전 역학

앙상블은 위상 공간에서의 확률 밀도 함수로 표현된다.^[2] 여기서 각 미시 상태는 위상 공간에서 특정 부피를 갖는 영역으로 나타내진다.^[8] 고전 역학에서 앙상블은 시스템의 위상 공간에 정의된 확률 밀도 함수로 표현된다. 개별 시스템은 해밀턴 방정식에 따라 움직이지만, 앙상블의 밀도 함수는 리우빌 방정식에 따라 시간에 따라 변화한다.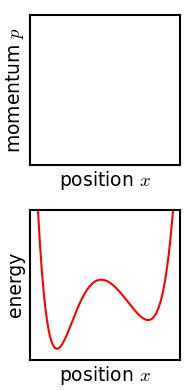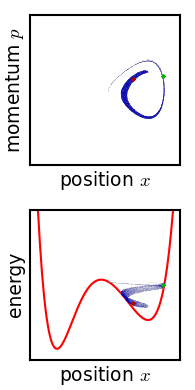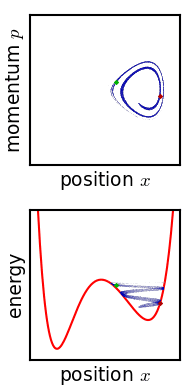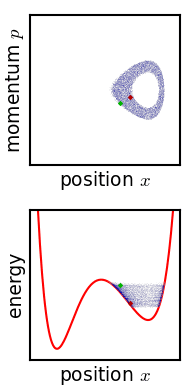

고전역학 시스템의 위상 공간에서의 앙상블 진화(위). 각 시스템은 1차원 포텐셜 우물 (빨간 곡선, 아래 그림) 내의 하나의 질량 입자로 구성. 처음에는 조밀했던 앙상블이 시간이 지남에 따라 소용돌이침.

정의된 부분의 수가 있는 역학 시스템에서 위상 공간은 n개의 일반화 좌표 (q1, ... qn)와 n개의 관련 정준 운동량 (p1, ... pn)을 가진다.

만약 앙상블 내 시스템 간에 시스템의 부분 수가 다르게 허용되는 경우 (예: 입자 수가 무작위 변수인 대앙상블), 확장된 위상 공간에 대한 확률 분포는 추가 변수 N1 (첫 번째 종류의 입자), N2 (두 번째 종류의 입자) 등을 포함하며, Ns (마지막 종류의 입자, s는 서로 다른 종류의 입자가 몇 개인지)까지 고려한다. 그러면 앙상블은 결합 확률 밀도 함수 ρ(N1, ... Ns, p1, ... pn, q1, ... qn)으로 표현된다. 여기서 좌표의 수 n은 입자 수에 따라 달라진다.

모든 역학적 양 X는 시스템 위상의 함수로 쓸 수 있으며, 이러한 양의 기댓값은 ρ로 가중된 이 양의 전체 위상 공간에 대한 적분으로 주어진다.

:

\langle X \rangle = \sum_{N_1 = 0}^{\infty} \ldots \sum_{N_s = 0}^{\infty} \int \ldots \int \rho X \, dp_1 \ldots dq_n.

확률 정규화 조건은 다음을 만족해야 한다.

:

\sum_{N_1 = 0}^{\infty} \ldots \sum_{N_s = 0}^{\infty} \int \ldots \int \rho \, dp_1 \ldots dq_n = 1.

위상 공간은 모든 작은 영역 내에 무한히 많은 수의 별개의 물리적 상태를 포함하는 연속적인 공간이다. 따라서 위상 공간의 확률 ''밀도''를 미시 상태에 대한 확률 ''분포''와 연결하려면, 위상 공간을 시스템의 서로 다른 상태를 나타내는 블록으로 나누어야 한다. 고전역학에서 미시 상태는 특정 부피를 갖는 정준 좌표의 위상 공간 내의 확장된 영역이다.^[8]

위상 공간의 확률 밀도 함수 ρ는 미시 상태에 대한 확률 분포 P와 다음과 같은 관계를 가진다.

:

\rho = \frac{1}{h^n C} P,

여기서

h는 energy×time 단위를 갖는 상수로서, 미시 상태의 범위를 설정하고 ρ에 올바른 차원을 제공한다.^[9]
C는 과잉 계산 보정 계수로, 일반적으로 입자 수 및 유사한 문제에 따라 달라진다.

h는 임의로 선택할 수 있지만, h의 값은 엔트로피 및 화학적 포텐셜과 같은 양의 오프셋에 영향을 미치므로 서로 다른 시스템을 비교할 때 h의 값을 일관성 있게 유지하는 것이 중요하다.

하지만 위상 공간은 여러 위치에 동일한 물리적 상태의 중복을 포함하는 경우가 많다. 이는 물리적 상태가 수학적 좌표로 표현되는 방식 때문이다. 예를 들어 동일한 입자 가스에서 두 입자가 교환되면 위상 공간의 결과 지점은 달라지지만, 시스템의 동일한 물리적 상태에 해당한다. 따라서 통계 역학에서는 위상 공간에서 적분할 때 실제 물리적 상태를 과도하게 계산하지 않는 것이 중요하다. 과잉 계산은 혼합 역설과 같은 문제를 야기할 수 있다.^[2]

과잉 계산을 보정하는 간단한 방법은 전체 위상 공간에 대해 적분하되, 각 위상의 가중치를 줄여 과도한 계산을 정확하게 보상하는 것이다. 이는 인자 C를 통해 수행되며, 이 값은 위상 공간에서 물리적 상태를 표현할 수 있는 횟수를 나타내는 정수이다. C는 연속적인 정준 좌표에 따라 달라지지 않으므로,^[11] 과잉 계산은 전체 범위의 정준 좌표를 적분한 다음 결과를 과잉 계산 인수로 나누어 보정할 수 있다. 단, C는 입자 수와 같은 이산 변수에 따라 크게 달라지므로, 입자 수에 대해 합산하기 전에 적용해야 한다.

예를 들어, 다양한 종류의 입자를 포함하는 유체 시스템에서 동일한 종류의 두 입자가 구별 불가능하고 교환 가능한 경우, 상태가 입자의 개별 위치와 운동량으로 기록되면 동일한 입자의 교환과 관련된 과도한 계산은 다음을 사용하여 수정된다.^[2]

:

C = N_1! N_2! \ldots N_s!.

이는 "볼츠만 보정"으로 알려져 있다.

5. 2. 양자 역학

앙상블은 주로 density matrix|밀도 행렬^영어로 표시되는^[1] 밀도 행렬로 표현된다.^[1] 밀도 행렬은 양자 불확정성(계의 상태를 완전히 알고 있는 경우에도 존재함)과 고전적 불확정성(지식 부족으로 인한)을 통합된 방식으로 포함할 수 있는 매우 일반적인 도구이다.^[1] 양자역학에서 임의의 물리적 관측량 X는 연산자

\hat X

로 작성할 수 있다.^[1] 통계적 앙상블

\rho

에 대한 이 연산자의 기대값은 다음 대각합으로 주어진다.^[1]

:

\langle X \rangle = \operatorname{Tr}(\hat X \rho).

이것은 평균(연산자

\hat X

), 분산 (연산자

\hat X^2

사용), 공분산 (연산자

\hat X \hat Y

사용) 등을 계산하는 데 사용할 수 있다.^[1] 밀도 행렬은 항상 대각합이 1이어야 한다:^[1]

\operatorname{Tr}{\hat\rho} = 1

(이것은 본질적으로 확률이 1이 되어야 한다는 조건이다).^[1]

일반적으로 앙상블은 폰 노이만 방정식에 따라 시간에 따라 진화한다.^[1]

평형 앙상블(시간에 따라 진화하지 않는 앙상블,

d\hat\rho / dt = 0

)은 보존 변수의 함수로만 작성할 수 있다.^[1] 예를 들어, 미시 정준 앙상블과 정준 앙상블은 총 에너지 연산자

\hat H

(해밀토니안)에 의해 측정되는 총 에너지의 엄격한 함수이다.^[1] 거시 정준 앙상블은 추가적으로 총 입자 수 연산자

\hat N

에 의해 측정되는 입자 수의 함수이다.^[1] 이러한 평형 앙상블은 각 보존 변수를 동시에 대각화하는 상태의 직교 기저에서 대각 행렬이다.^[1] 브라-켓 표기법에서 밀도 행렬은 다음과 같다.^[1]

:

\hat\rho = \sum_i P_i |\psi_i\rangle \langle\psi_i|,

여기서

|\psi_i\rangle

, i로 인덱싱되며, 완전하고 직교 기저의 요소이다.^[1] (다른 기저에서는 밀도 행렬이 반드시 대각선은 아니다.)^[1]

6. 에르고드 가설

에르고드 가설은 충분히 긴 시간 동안, 시스템이 가능한 모든 미시 상태를 거친다는 가설이다. 이 가설이 성립하면 시간 평균과 앙상블 평균이 같아진다.

만약 시간이 지남에 따라 계가 가능한 모든 미시 상태, 즉 모든 위상 공간 좌표를 한 번씩이라도 지나가게 된다면, $=$ 를 만족한다. 이러한 조건을 '''에르고드 가설'''(ergodic hypothesis)이라 부른다. 오랜 시간이 지나 정상 상태 혹은 준평형 상태에 도달하는 역학적 계에 대해 위 가설이 성립한다.

7. 리우빌 정리

밀도함수의 시간변화율은 다음 식과 같이 기술될 수 있다.

: $\frac{d\rho}{dt}=\frac{\partial\rho}{\partial t}+\{\rho,H\}=0$

이를 조제프 리우빌의 이름을 따 '''리우빌 정리'''(Liouville's theorem^영어)라 한다.^[1] 여기서 $\{\rho,H\}$ 는 푸아송 괄호이다.^[1]

밀도 함수가 시간과 직접적인 관련이 없다고 가정하면 밀도 함수의 시간 편미분 계수는 0이 되므로, 다음 식을 만족할 경우 밀도 함수의 시간 변화율이 0이 되어 밀도 함수는 시간에 대해 불변하는 값이 된다.^[1]

: $\{\rho,H\}=0$

따라서 위 식을 만족하면 평형 상태에서 계의 특성을 기술하는 통계역학적 기술이 가능하다.^[1] 위 식을 만족하는 두 가지 경우는 첫째로

: $\rho({q_i},{p_i})=Const.$

일 때와, 두 번째로 밀도 함수가 해밀토니언의 함수

: $\rho({q_i},{p_i})=\rho(H({q_i},{p_i}))$

일 때로 나뉘며, 전자의 경우를 만족하는 앙상블을 작은 바른틀 앙상블, 후자의 경우를 만족하는 앙상블을 바른틀 앙상블이라 한다.^[1]

8. 통계역학의 응용

물리학에서 사용되는 통계적 앙상블 공식은 정준 앙상블 또는 깁스 측정이 일련의 제약 조건 하에서 시스템의 엔트로피를 최대화하는 데 기여한다는 것이 인식되면서 다른 분야에서도 널리 채택되었다. 이것이 바로 최대 엔트로피 원리이다. 이 원리는 현재 언어학, 로봇 공학 등과 같은 문제에 광범위하게 적용되고 있다.

또한, 물리학의 통계적 앙상블은 종종 지역성 원리에 기반을 두고 있는데, 이는 모든 상호작용이 인접한 원자 또는 근처 분자 사이에서만 발생한다는 것이다. 따라서, 격자 모형의 일종인 이징 모형은 스핀 간의 가장 가까운 이웃 상호작용을 통해 강자성체를 모델링한다. 지역성 원리의 통계적 공식은 이제 광범위한 의미에서 마르코프 성질의 한 형태로 간주된다. 가장 가까운 이웃은 마르코프 블랭킷이다. 따라서 가장 가까운 이웃 상호작용이 있는 통계적 앙상블의 일반적인 개념은 마르코프 랜덤 필드로 이어지며, 이는 홉필드 네트워크 등 다양한 분야에 적용된다.

참조

_[1] 간행물 Oxford Dictionary of Physics
_[2] 서적 Elementary Principles in Statistical Mechanics Charles Scribner's Sons
_[3] 서적 Thermal Physics, Second Edition W.H. Freeman and Company
_[4] 서적 Statistical Physics Pergamon Press
_[5] 서적 The Collected Works, Vol. 2. Longmans.
_[6] 논문 Simulation of chemical reaction equilibria by the reaction ensemble Monte Carlo method: a review Informa UK Limited
_[7] 논문 "Ensemble inequivalence in single-molecule experiments" https://journals.aps[...] 2009-05-18
_[8] 문서 Liouville's theorem
_[9] 문서 Planck constant
_[10] 문서 Charts on SO(3)
_[11] 문서 Measure
_[12] 웹사이트 Statistical mechanics of classical systems http://physics.gmu.e[...] 2023-11-03
_[13] 문서 久保『熱学・統計力学』
_[14] 문서 北孝文『演習しよう熱・統計力学』
_[15] 문서 田崎『統計力学Ⅰ』
_[16] 문서 田崎『統計力学Ⅱ』
_[17] 문서 田崎『統計力学Ⅰ』
_[18] 문서 田崎『統計力学Ⅰ』
_[19] 문서 田崎『統計力学Ⅰ』
_[20] 문서 田崎『統計力学Ⅱ』
_[21] 문서 田崎『統計力学Ⅱ』

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com