오일러 수 (조합론)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

오일러 수(Eulerian number)는 조합론에서 다루어지는 수로, 순열의 성질과 관련된 여러 가지 정의와 성질을 갖는다. 오일러 수는 일반적으로 $\left\langle{n\atop m}\right\rangle$ 으로 표기하며, 이는 집합 {1, 2, ..., n}의 순열에서 'i' > 'i+1'인 'i'가 정확히 'm'개 있는 순열들의 개수를 의미한다. 오일러 다항식은 오일러 수를 계수로 하는 다항식으로, 지수 생성 함수를 통해 정의되기도 한다. 오일러 수는 명시적인 공식을 통해 계산할 수 있으며, 재귀 관계를 이용하여 더 큰 값에 대해서도 계산이 가능하다. 오일러 수는 오일러 삼각형 또는 오일러의 삼각형이라 불리는 삼각 배열 형태로 나타낼 수 있으며, 파스칼의 삼각형과 유사한 특징을 공유한다. 또한, 오일러 수는 합 공식, Worpitzky 항등식, 교대 합 공식 등 다양한 항등식을 만족하며, 수열의 거듭제곱의 생성 함수와도 관련이 있다. 2차 오일러 수는 멀티셋의 순열에서 상승의 개수를 계산하며, 2차 오일러 다항식과 재귀 관계를 통해 정의된다.

2. 정의

'''오일러 수'''(Eulerian number)는 다음 식으로 정의된다.

: $\left\langle{n\atop m}\right\rangle=\sum_{k=0}^m(-1)^k \binom{n+1}{k} (m+1-k)^n$

$A(n,m)$ 또는 $E(n,m)$ 으로 표기하기도 한다. 오일러 수는 순열을 이용하거나, 오일러 다항식을 이용하여 정의할 수 있다.

2. 1. 순열을 이용한 정의

오일러 수

\textstyle\left\langle{n\atop m}\right\rangle

는

\{1,2,\ldots,n\}

집합의 순열

a_1,a_2,\dots,a_n

가운데,

a_i>a_{i+1}

인

i

가 정확히

m

개 있는 순열의 개수이다. 즉, 순열을 기본적으로 증가하는 것으로 간주할 때, "역행"이

m

번 일어나는

n

원소 순열의 개수이다.

2. 2. 다항식을 이용한 정의

'''오일러 다항식'''

A_n(x)

은 오일러 수를 계수로 하는 다항식이다.^[1]

:

A_n(x)=\sum_{m=0}^n\left\langle{n\atop m}\right\rangle x^m

오일러 다항식

A_n(t)

의 지수 생성 함수는 다음과 같다.

:

\sum_{n=0}^{\infty} A_{n}(t) \,\frac{x^n}{n!} = \frac{t-1}{t - e^{(t-1)\,x}}.

오일러 수

A(n,k)

는 오일러 다항식의 계수로 정의할 수 있다.

:

A_{n}(t) = \sum_{k=0}^n A(n,k)\,t^k.

A(n,k)

에 대한 명시적 공식은 다음과 같다.

:

:

A(n,k)=\sum_{i=0}^{k}(-1)^i \binom{n+1}{i} (k+1-i)^n.

3. 역사

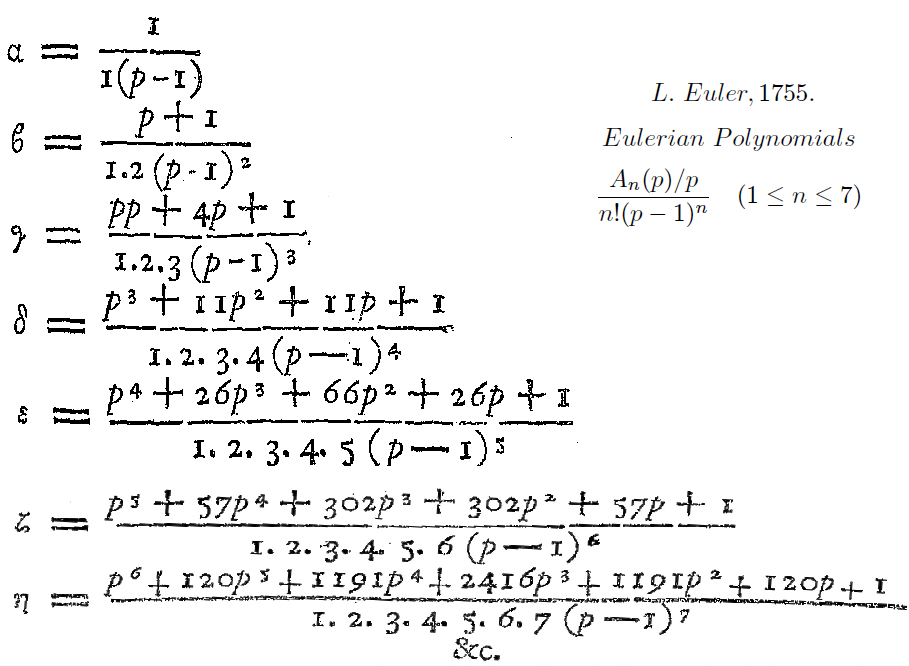
오일러 수와 오일러 다항식은 1755년 레온하르트 오일러의 저서 《미분학의 기초 및 유한 해석과 급수에 대한 응용》(Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum^la)^[5]에서 처음 등장한다. 이 책에 나오는 다항식

\alpha_1(x)

,

\alpha_2(x)

등은 오늘날의 오일러 다항식과는 약간 다르지만, 기본적으로 같은 대상이다.

4. 성질

낮은 차수의 오일러 수는 다음과 같다. 이러한 표를 '''오일러 삼각형'''이라고 하며, 파스칼 삼각형과 여러 유사한 성질을 가진다. ''n''번째 행의 수들의 합은 $n!$ 이다.^[1]

n \ m	0	1	2	3	4	5	6	7	8
1	1
2	1	1
3	1	4	1
4	1	11	11	1
5	1	26	66	26	1
6	1	57	302	302	57	1
7	1	120	1191	2416	1191	120	1
8	1	247	4293	15619	15619	4293	247	1
9	1	502	14608	88234	156190	88234	14608	502	1

$0 \le n \le 9$ 에 대한 $A(n, k)$ 의 값은 위 표와 같다.

4. 1. 기본 성질

고정된 ''n''에 대해 상승이 0개인 순열은 (n, n-1, n-2, …, 1) 하나뿐이다. 실제로 모든 $n$ 에 대해 ${\tbinom n 0}=1$ 이므로, $A(n, 0) = 1$ 이다. 이는 숫자들의 빈 집합( $n=0$ )을 형식적으로 포함한다. 따라서 $A_0(t)=A_1(t)=1$ 이다.
$k=1$ 일 때, 명시적 공식은 $A(n,1)=2^n-(n+1)$ 이며, 이는 $n$ 에 대한 수열로 0, 0, 1, 4, 11, 26, 57, …로 나타난다.
''k''개의 상승을 가진 순열을 완전히 뒤집으면 ''n-k-1''개의 상승을 가진 다른 순열이 만들어진다. 따라서 $A(n, k) = A(n, n-k-1)$ 이다. 그러므로 ''n-1''개의 상승을 가진 순열도 (1, 2, …, n) 하나뿐이며, $A(n, n-1)$ 또한 1이다.
과도한 상한은 $A(n, k) \le (k+1)^n\cdot(n+2)^k$ 이다. 방금 논의한 경계 사이에서, 값은 1을 초과한다.
$k\ge n > 0$ 일 때, 값은 형식적으로 0이다. 이는 $k$ 에 대한 많은 합이 상한 지수를 $n-1$ 까지만 쓸 수 있음을 의미한다. 또한 다항식 $A_{n}(t)$ 가 $n>0$ 에 대해 실제로 차수 $n-1$ 임을 의미한다.

삼각 배열의 숫자 표는 '''오일러 삼각형''' 또는 '''오일러의 삼각형'''이라고 하며, 파스칼의 삼각형과 몇 가지 공통적인 특징을 공유한다.

0 \le n \le 9

에 대한

A(n, k)

의 값은 다음과 같다.

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	1
3	1	4	1
4	1	11	11	1
5	1	26	66	26	1
6	1	57	302	302	57	1
7	1	120	1191	2416	1191	120	1
8	1	247	4293	15619	15619	4293	247	1
9	1	502	14608	88234	156190	88234	14608	502	1

4. 2. 오일러 삼각형

파스칼 삼각형과 여러 유사한 성질을 가지는 '''오일러 삼각형'''은 다음과 같다.^[1]

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	1
3	1	4	1
4	1	11	11	1
5	1	26	66	26	1
6	1	57	302	302	57	1
7	1	120	1191	2416	1191	120	1
8	1	247	4293	15619	15619	4293	247	1
9	1	502	14608	88234	156190	88234	14608	502	1

오일러 삼각형의 ''n''번째 행의 수들의 합은 $n!$ 이다.^[1]

고정된 '' $n$ ''에 대해 상승이 0개인 순열은 (n, n-1, n-2, ..., 1) 하나뿐이다. ''k''개의 상승을 가진 순열을 뒤집으면 ''n-k-1''개의 상승을 가진 순열이 생성되므로, $A(n, k) = A(n, n-k-1)$ 이다. 따라서 ''n-1''개의 상승을 가진 순열도 (1, 2, ..., n) 하나뿐이다. $k=1$ 에 대한 명시적 공식은 $A(n,1)=2^n-(n+1)$ 이며, 이는 ''n''에 대한 수열로 0, 0, 1, 4, 11, 26, 57, ... 로 나타낸다.^[1]

5. 계산

오일러 수 $A(n,k)$ 는 재귀 공식을 이용하여 계산할 수 있다. 이 공식은 조합론적 정의에서 비롯된다. 작은 값의 ''n''과 ''k''에 대해서는 손으로 계산할 수 있으며, 더 큰 값의 $n$ 에 대해서는 재귀 공식을 이용한다.

5. 1. 재귀적 공식

A(n,k)=(n-k)A(n-1,k-1) + (k+1)A(n-1,k)

의 재귀 공식을 사용하여 더 큰

n

에 대한

A(n,k)

를 계산할 수 있다. 이 공식은 조합론적 정의에서 비롯된다.

작은

n

과

k

값에 대해

A(n,k)

의 값을 손으로 계산할 수 있다.

n	k	순열	A(n, k)
1	0	(1)	A(1,0) = 1
2	0	(2, 1)	A(2,0) = 1
2	1	(1, 2)	A(2,1) = 1
3	0	(3, 2, 1)	A(3,0) = 1
	1	(1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2)	A(3,1) = 4
	2	(1, 2, 3)	A(3,2) = 1

재귀 공식을 적용하면, $A(4,1)=(4-1)A(3,0) + (1+1)A(3,1)=3 \cdot 1 + 2 \cdot 4 = 11$ 을 얻을 수 있다.

오일러 다항식은 다음 재귀식으로 계산할 수 있다.

: $A_{0}(t) = 1,$

: $A_{n}(t) = A_{n-1}'(t)\cdot t(1-t) + A_{n-1}(t)\cdot (1+(n-1)t),\text{ for } n > 1.$

두 번째 공식은 귀납적 형태로 표현될 수 있다.

: $A_{n}(t) = \sum_{k=0}^{n-1} \binom{n}{k} A_{k}(t)\cdot (t-1)^{n-1-k}, \text{ for } n > 1.$

5. 2. 오일러 다항식의 재귀식

:

A(n,k)=(n-k)\,A(n-1,k-1) + (k+1)\,A(n-1,k)

이 공식은 조합론적 정의에서 비롯될 수 있으며, 따라서 이론의 자연스러운 출발점을 제공한다.

작은 값의 ''n''과 ''k''에 대해,

A(n,k)

의 값은 손으로 계산할 수 있다. 예를 들어 아래 표와 같다.

n	k	순열	A(n, k)
1	0	(1)	A(1,0) = 1
2	0	(2, 1)	A(2,0) = 1
2	1	(1, 2)	A(2,1) = 1
3	0	(3, 2, 1)	A(3,0) = 1
	1	(1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2)	A(3,1) = 4
	2	(1, 2, 3)	A(3,2) = 1

재귀 공식을 한 예에 적용하면 다음을 얻을 수 있다.

: $A(4,1)=(4-1)\,A(3,0) + (1+1)\,A(3,1)=3 \cdot 1 + 2 \cdot 4 = 11.$

마찬가지로, 오일러 다항식은 다음 재귀식으로 계산할 수 있다.

: $A_{0}(t) = 1,$

: $A_{n}(t) = A_{n-1}'(t)\cdot t\,(1-t) + A_{n-1}(t)\cdot (1+(n-1)\,t),\text{ for } n > 1.$

두 번째 공식은 귀납적 형태로 표현될 수 있다.

: $A_{n}(t) = \sum_{k=0}^{n-1} \binom{n}{k} A_{k}(t)\cdot (t-1)^{n-1-k}, \text{ for } n > 1.$

6. 항등식

오일러 수는 여러 항등식에서 나타난다.

유한 집합의 분할 성질에 의해, 오일러 수의 합은 계승이 된다.^[2]
보르피츠키(Worpitzky) 항등식은^[3] xⁿ을 이항 계수와 오일러 수의 선형 결합으로 표현한다.

6. 1. 합 공식

유한 집합을 유한 개의 더 작은 집합으로 분할하는 모든 속성에 대해, 더 작은 집합들의 기수의 합은 더 큰 집합의 기수와 같다. 오일러 수는

n

개의 원소의 순열을 분할하므로, 그 합은 계승

n!

과 같다. 즉, 다음과 같다.

:

\sum_{k=0}^{n-1} A(n,k) = n!, \text{ for }n > 0.

그리고

A(0,0)=0!

이다. 빈 합 규칙과의 충돌을 피하기 위해,

n>0

에 대한 정리를 서술한다.

훨씬 더 일반적으로, 구간

(0, n)

에서 적분 가능한 고정 함수

f\colon \mathbb{R} \rightarrow \mathbb{C}

에 대해 다음이 성립한다.^[2]

:

\sum_{k=0}^{n-1} A(n, k)\, f(k) = n!\int_0^1 \cdots \int_0^1 f\left(\left\lfloor x_1 + \cdots + x_n\right\rfloor\right) {\mathrm d}x_1 \cdots {\mathrm d}x_n

'''보르피츠키 항등식'''^[3]은

x^n

을 이항 계수와 함께 오일러 수의 선형 결합으로 표현한다.

:

\sum_{k=0}^{n-1}A(n,k)\binom{x+k}{n}=x^n.

이로부터 다음이 유도된다.

:

\sum_{k=1}^{m}k^n=\sum_{k=0}^{n-1} A(n,k) \binom{m+k+1}{n+1}.

6. 2. Worpitzky 항등식

유한 집합을 유한 개의 더 작은 집합으로 분할하는 모든 속성에 대해, 더 작은 집합들의 기수의 합은 더 큰 집합의 기수와 같다. 오일러 수는

n

개의 원소의 순열을 분할하므로, 그 합은 계승

n!

과 같다. 즉, 다음이 성립한다.

:

\sum_{k=0}^{n-1} A(n,k) = n!, \text{ for }n > 0.

그리고

A(0,0)=0!

이다. 빈 합 규칙과의 충돌을 피하기 위해,

n>0

에 대한 정리만 나타내는 것이 편리하다.

훨씬 더 일반적으로, 구간

(0, n)

에서 적분 가능한 고정 함수

f\colon \mathbb{R} \rightarrow \mathbb{C}

에 대해 다음이 성립한다.^[2]

:

\sum_{k=0}^{n-1} A(n, k)\, f(k) = n!\int_0^1 \cdots \int_0^1 f\left(\left\lfloor x_1 + \cdots + x_n\right\rfloor\right) {\mathrm d}x_1 \cdots {\mathrm d}x_n

'''보르피츠키 항등식'''^[3]은

x^n

을 이항 계수와 함께 오일러 수의 선형 결합으로 표현한다.

:

\sum_{k=0}^{n-1}A(n,k)\binom{x+k}{n}=x^n.

보르피츠키 항등식으로부터 다음이 유도된다.

:

\sum_{k=1}^{m}k^n=\sum_{k=0}^{n-1} A(n,k) \binom{m+k+1}{n+1}.

6. 3. 교대 합 공식

유한 집합을 유한 개의 더 작은 집합으로 분할하는 모든 속성에 대해, 더 작은 집합들의 기수의 합은 더 큰 집합의 기수와 같다. 오일러 수는

n

개의 원소의 순열을 분할하므로, 그 합은 계승

n!

과 같다. 즉,

:

\sum_{k=0}^{n-1} A(n,k) = n!, \text{ for }n > 0.

그리고

A(0,0)=0!

이다. 빈 합 규칙과의 충돌을 피하기 위해,

n>0

에 대한 정리를 서술한다.

훨씬 더 일반적으로, 구간

(0, n)

에서 적분 가능한 고정 함수

f\colon \mathbb{R} \rightarrow \mathbb{C}

에 대해^[2]

:

\sum_{k=0}^{n-1} A(n, k)\, f(k) = n!\int_0^1 \cdots \int_0^1 f\left(\left\lfloor x_1 + \cdots + x_n\right\rfloor\right) {\mathrm d}x_1 \cdots {\mathrm d}x_n

'''보르피츠키 항등식'''^[3]은

x^n

을 이항 계수와 함께 오일러 수의 선형 결합으로 표현한다.

:

\sum_{k=0}^{n-1}A(n,k)\binom{x+k}{n}=x^n.

이로부터 다음이 따른다.

:

\sum_{k=1}^{m}k^n=\sum_{k=0}^{n-1} A(n,k) \binom{m+k+1}{n+1}.

고정된 ''

n

''에 대한 오일러 수의 교대합은 베르누이 수

B_{n+1}

과 관련이 있다.

:

\sum_{k=0}^{n-1}(-1)^k A(n,k) = 2^{n+1}(2^{n+1}-1) \frac{B_{n+1}}{n+1}, \text{  for  }n > 0.

또한,

:

\sum_{k=0}^{n-1}(-1)^k \frac{A(n,k)}{\binom{n-1}{k}}=0, \text{  for  }n > 1

그리고

:

\sum_{k=0}^{n-1}(-1)^k \frac{A(n,k)}{\binom{n}{k}}=(n+1)B_{n}, \text{  for  } n > 1

6. 4. 다항식 관련 공식

유한 집합을 유한 개의 더 작은 집합으로 분할하는 모든 속성에 대해, 더 작은 집합들의 기수의 합은 더 큰 집합의 기수와 같습니다. 오일러 수는

n

개의 원소의 순열을 분할하므로, 그 합은 계승

n!

과 같습니다. 즉,

:

\sum_{k=0}^{n-1} A(n,k) = n!, \text{ for }n > 0.

그리고

A(0,0)=0!

입니다. 빈 합 규칙과의 충돌을 피하기 위해,

n>0

에 대한 정리를 서술합니다.

구간

(0, n)

에서 적분 가능한 고정 함수

f\colon \mathbb{R} \rightarrow \mathbb{C}

에 대해,^[2]

:

\sum_{k=0}^{n-1} A(n, k)\, f(k) = n!\int_0^1 \cdots \int_0^1 f\left(\left\lfloor x_1 + \cdots + x_n\right\rfloor\right) {\mathrm d}x_1 \cdots {\mathrm d}x_n

'''보르피츠키 항등식'''^[3]은

x^n

을 이항 계수와 함께 오일러 수의 선형 결합으로 표현합니다.

:

\sum_{k=0}^{n-1}A(n,k)\binom{x+k}{n}=x^n.

이로부터 다음이 유도됩니다.

:

\sum_{k=1}^{m}k^n=\sum_{k=0}^{n-1} A(n,k) \binom{m+k+1}{n+1}.

오일러 다항식의 대칭성은 다음을 의미합니다.

:

A_n(t) = t^{n-1} A_n(t^{-1})

오일러 수는 수열의 ''n''^th 거듭제곱의 생성 함수에 포함됩니다.

:

\sum_{i=1}^\infty i^n x^i = \frac{1}{(1-x)^{n+1}}\sum_{k=0}^n A(n,k)\,x^{k+1} = \frac{x}{(1-x)^{n+1}}A_n(x)

오일러 다항식에 대한 명시적인 표현은 다음과 같습니다.^[4]

A_n(t) = \sum_{k=0}^n \left\{ {n \atop k} \right\} k! (t-1)^{n-k}

여기서

\left\{ {n \atop k} \right\}

는 제2종 스털링 수입니다.

7. 2차 오일러 수

2차 오일러 수는 멀티셋 {1, 1, 2, 2, ..., n, n}의 순열 중, 'k'의 두 번의 출현 사이에 나타나는 모든 숫자가 'k'보다 큰 속성을 가진 순열에서, 정확히 ''m''개의 상승을 갖는 순열의 수를 나타낸다. 2차 오일러 수와 관련된 내용은 다음 세 가지 방식으로 인덱싱되어 제공된다.

Riordan과 Comtet를 따름
Graham, Knuth 및 Patashnik을 따름
Gessel과 Stanley의 정의를 확장

7. 1. 정의

멀티셋 {1, 1, 2, 2, \ldots, n, n}의 순열에서, ''k''의 두 번의 출현 사이에 나타나는 모든 숫자가 ''k''보다 큰 속성을 가진 순열은 이중 계승 수 (2''n''-1)!!로 계산된다.

2차 오일러 수

\scriptstyle \left\langle \! \left\langle {n \atop m} \right\rangle \! \right\rangle

는 정확히 ''m''개의 상승을 갖는 모든 그러한 순열의 수를 계산한다. 예를 들어, ''n'' = 3인 경우 그러한 순열은 15개이며, 상승이 없는 순열 1개, 상승이 1개인 순열 8개, 상승이 2개인 순열 6개가 있다.

: 332211,

: 221133, 221331, 223311, 233211, 113322, 133221, 331122, 331221,

: 112233, 122133, 112332, 123321, 133122, 122331.

2차 오일러 수는 다음 재귀 관계를 만족하며, 이는 위 정의에서 직접 파생된다.

:

\left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle = (2n-k-1) \left\langle \!\! \left\langle {n-1 \atop k-1} \right\rangle \!\! \right\rangle + (k+1) \left\langle \!\! \left\langle {n-1 \atop k} \right\rangle \!\! \right\rangle,

아이버슨 괄호 표기법으로 표현된 ''n'' = 0에 대한 초기 조건은 다음과 같다.

:

\left\langle \!\! \left\langle {0 \atop k} \right\rangle \!\! \right\rangle = [k=0].

이에 따라, 2차 오일러 다항식은 ''P''_''n''으로 표시된다(이에 대한 표준 표기법은 없다).

:

P_n(x) := \sum_{k=0}^n  \left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle x^k

위의 재귀 관계는 수열 ''P''_''n''(''x'')에 대한 재귀 관계로 변환된다.

:

P_{n+1}(x) = (2nx+1) P_n(x) - x(x-1) P_n^\prime(x)

초기 조건은

P_0(x) = 1

이다. 후자의 재귀 관계는 적분 인수를 사용하여 약간 더 간결한 형태로 작성할 수 있다.

:

(x-1)^{-2n-2} P_{n+1}(x) = \left( x\,(1-x)^{-2n-1} P_n(x) \right)^\prime

따라서 유리 함수

:

u_n(x) := (x-1)^{-2n} P_{n}(x)

는 단순한 자율 재귀를 만족한다.

:

u_{n+1} = \left( \frac{x}{1-x} u_n \right)^\prime, \quad u_0=1

여기에서 2차 오일러 다항식은

P_n(x) = (1-x)^{2n} u_n(x)

로, 2차 오일러 수는 해당 계수로 얻는다.

다음 표는 처음 몇 개의 2차 오일러 수를 표시한다.

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	2
3	1	8	6
4	1	22	58	24
5	1	52	328	444	120
6	1	114	1452	4400	3708	720
7	1	240	5610	32120	58140	33984	5040
8	1	494	19950	195800	644020	785304	341136	40320
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880

''n''번째 행의 합, 즉 $P_n(1)$ 의 값은 $(2n-1)!!$ 이다.

2차 오일러 수의 인덱싱은 세 가지 방식으로 제공된다.

Riordan과 Comtet를 따름
Graham, Knuth 및 Patashnik을 따름
, Gessel과 Stanley의 정의를 확장

7. 2. 재귀 관계

멀티셋

\{1, 1, 2, 2, \ldots, n, n\}

의 순열에서 ''k''의 두 번의 출현 사이에 나타나는 모든 숫자가 ''k''보다 큰 속성을 가진 순열은 이중 계승 수

(2n-1)!!

로 계산된다. 2차 오일러 수

\scriptstyle \left\langle \! \left\langle {n \atop m} \right\rangle \! \right\rangle

는 정확히 ''m''개의 상승을 갖는 모든 그러한 순열의 수를 나타낸다. 예를 들어 ''n'' = 3인 경우, 그러한 순열은 15개이며, 상승이 없는 순열 1개, 상승이 1개인 순열 8개, 상승이 2개인 순열 6개가 있다.

: 332211,

: 221133, 221331, 223311, 233211, 113322, 133221, 331122, 331221,

: 112233, 122133, 112332, 123321, 133122, 122331.

2차 오일러 수는 다음 재귀 관계를 만족하며, 이는 위 정의에서 직접 유도된다.

:

\left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle = (2n-k-1) \left\langle \!\! \left\langle {n-1 \atop k-1} \right\rangle \!\! \right\rangle + (k+1) \left\langle \!\! \left\langle {n-1 \atop k} \right\rangle \!\! \right\rangle,

아이버슨 괄호 표기법으로 표현된 ''n'' = 0에 대한 초기 조건은 다음과 같다.

:

\left\langle \!\! \left\langle {0 \atop k} \right\rangle \!\! \right\rangle = [k=0].

이에 따라, 2차 오일러 다항식은 ''P''_''n''으로 표시된다(이에 대한 표준 표기법은 없다).

:

P_n(x) := \sum_{k=0}^n  \left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle x^k

위의 재귀 관계는 수열 ''P''_''n''(''x'')에 대한 다음 재귀 관계로 변환된다.

:

P_{n+1}(x) = (2nx+1) P_n(x) - x(x-1) P_n^\prime(x)

초기 조건은

P_0(x) = 1

이다. 후자의 재귀 관계는 적분 인수를 사용하여 다음과 같이 더 간결한 형태로 작성할 수 있다.

:

(x-1)^{-2n-2} P_{n+1}(x) = \left( x\,(1-x)^{-2n-1} P_n(x) \right)^\prime

따라서 유리 함수

:

u_n(x) := (x-1)^{-2n} P_{n}(x)

는 다음의 자율 재귀를 만족한다.

:

u_{n+1} = \left( \frac{x}{1-x} u_n \right)^\prime, \quad u_0=1

여기에서 2차 오일러 다항식은

P_n(x) = (1-x)^{2n} u_n(x)

로, 2차 오일러 수는 해당 계수로 얻어진다.

다음 표는 처음 몇 개의 2차 오일러 수를 나타낸다.

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	2
3	1	8	6
4	1	22	58	24
5	1	52	328	444	120
6	1	114	1452	4400	3708	720
7	1	240	5610	32120	58140	33984	5040
8	1	494	19950	195800	644020	785304	341136	40320
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880

''n''번째 행의 합, 즉 $P_n(1)$ 의 값은 $(2n-1)!!$ 이다.

2차 오일러 수의 인덱싱은 세 가지 방식으로 제공된다.

7. 3. 2차 오일러 다항식

멀티셋 \{1, 1, 2, 2, \ldots, n, n\}의 순열에서, ''k''의 두 번의 출현 사이에 나타나는 모든 숫자가 ''k''보다 큰 속성을 가진 순열은 이중 계승 수 (2n-1)!!로 계산된다.

2차 오일러 수

\scriptstyle \left\langle \! \left\langle {n \atop m} \right\rangle \! \right\rangle

는 정확히 ''m''개의 상승을 갖는 모든 그러한 순열의 수를 나타낸다. 예를 들어 ''n'' = 3인 경우, 그러한 순열은 15개이며, 상승이 없는 순열 1개, 상승이 1개인 순열 8개, 상승이 2개인 순열 6개가 있다.

: 332211,

: 221133, 221331, 223311, 233211, 113322, 133221, 331122, 331221,

: 112233, 122133, 112332, 123321, 133122, 122331.

2차 오일러 수는 다음 재귀 관계를 만족하며, 이는 위 정의에서 직접 유도된다.

:

\left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle = (2n-k-1) \left\langle \!\! \left\langle {n-1 \atop k-1} \right\rangle \!\! \right\rangle + (k+1) \left\langle \!\! \left\langle {n-1 \atop k} \right\rangle \!\! \right\rangle,

아이버슨 괄호 표기법으로 표현된 ''n'' = 0에 대한 초기 조건은 다음과 같다.

:

\left\langle \!\! \left\langle {0 \atop k} \right\rangle \!\! \right\rangle = [k=0].

이에 따라, 2차 오일러 다항식 ''P''_''n''(표준 표기법은 없음)은 다음과 같이 정의된다.

:

P_n(x) := \sum_{k=0}^n  \left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle x^k

위의 재귀 관계는 수열 ''P''_''n''(''x'')에 대한 재귀 관계로 변환된다.

:

P_{n+1}(x) = (2nx+1) P_n(x) - x(x-1) P_n^\prime(x)

초기 조건은

P_0(x) = 1

이다. 후자의 재귀 관계는 적분 인수를 사용하여 더 간결하게 표현할 수 있다.

:

(x-1)^{-2n-2} P_{n+1}(x) = \left( x\,(1-x)^{-2n-1} P_n(x) \right)^\prime

따라서 유리 함수

:

u_n(x) := (x-1)^{-2n} P_{n}(x)

는 단순한 자율 재귀를 만족한다.

:

u_{n+1} = \left( \frac{x}{1-x} u_n \right)^\prime, \quad u_0=1

여기에서 2차 오일러 다항식은

P_n(x) = (1-x)^{2n} u_n(x)

로, 2차 오일러 수는 해당 계수로 얻어진다.

다음 표는 처음 몇 개의 2차 오일러 수를 나타낸다.

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	2
3	1	8	6
4	1	22	58	24
5	1	52	328	444	120
6	1	114	1452	4400	3708	720
7	1	240	5610	32120	58140	33984	5040
8	1	494	19950	195800	644020	785304	341136	40320
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880

''n''번째 행의 합, 즉 $P_n(1)$ 의 값은 $(2n-1)!!$ 이다.

2차 오일러 수의 인덱싱은 세 가지 방식으로 제공된다.

Riordan과 Comtet를 따름
Graham, Knuth 및 Patashnik을 따름
Gessel과 Stanley의 정의를 확장

7. 4. 표

n ＼ k	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	2
3	1	8	6
4	1	22	58	24
5	1	52	328	444	120
6	1	114	1452	4400	3708	720
7	1	240	5610	32120	58140	33984	5040
8	1	494	19950	195800	644020	785304	341136	40320
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880

''n''번째 행의 합, 즉 $P_n(1)$ 의 값은 이중 계승 $(2n-1)!!$ 이다.

7. 5. 인덱싱

멀티셋

\{1, 1, 2, 2, \ldots, n, n\}

의 순열 중, ''k''의 두 번의 출현 사이에 나타나는 모든 숫자가 ''k''보다 큰 속성을 가진 순열은 이중 계승 수

(2n-1)!!

로 계산된다. 2차 오일러 수

\scriptstyle \left\langle \! \left\langle {n \atop m} \right\rangle \! \right\rangle

는 정확히 ''m''개의 상승을 갖는 모든 그러한 순열의 수를 계산한다. 예를 들어 ''n'' = 3인 경우, 그러한 순열은 15개이며, 상승이 없는 순열 1개, 상승이 1개인 순열 8개, 상승이 2개인 순열 6개가 있다.

: 332211,

: 221133, 221331, 223311, 233211, 113322, 133221, 331122, 331221,

: 112233, 122133, 112332, 123321, 133122, 122331.

2차 오일러 수는 다음 재귀 관계를 만족하며, 이는 위 정의에서 직접 파생된다.

:

\left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle = (2n-k-1) \left\langle \!\! \left\langle {n-1 \atop k-1} \right\rangle \!\! \right\rangle + (k+1) \left\langle \!\! \left\langle {n-1 \atop k} \right\rangle \!\! \right\rangle,

아이버슨 괄호 표기법으로 표현된 ''n'' = 0에 대한 초기 조건:

:

\left\langle \!\! \left\langle {0 \atop k} \right\rangle \!\! \right\rangle = [k=0].

이에 따라, 2차 오일러 다항식은 ''P''_''n''으로 표시된다(이에 대한 표준 표기법은 없다).

:

P_n(x) := \sum_{k=0}^n  \left\langle \!\! \left\langle {n \atop k} \right\rangle \!\! \right\rangle x^k

위의 재귀 관계는 수열 ''P''_''n''(''x'')에 대한 재귀 관계로 변환된다.

:

P_{n+1}(x) = (2nx+1) P_n(x) - x(x-1) P_n^\prime(x)

초기 조건

P_0(x) = 1.

이다. 후자의 재귀 관계는 적분 인수를 사용하여 약간 더 간결한 형태로 작성할 수 있다.

:

(x-1)^{-2n-2} P_{n+1}(x) = \left( x\,(1-x)^{-2n-1} P_n(x) \right)^\prime

따라서 유리 함수

:

u_n(x) := (x-1)^{-2n} P_{n}(x)

는 단순한 자율 재귀를 만족한다.

:

u_{n+1} = \left( \frac{x}{1-x} u_n \right)^\prime, \quad u_0=1

여기에서 2차 오일러 다항식은

P_n(x) = (1-x)^{2n} u_n(x)

로, 2차 오일러 수는 해당 계수로 얻는다.

다음 표는 처음 몇 개의 2차 오일러 수를 표시한다.

	0	1	2	3	4	5	6	7	8
0	1
1	1
2	1	2
3	1	8	6
4	1	22	58	24
5	1	52	328	444	120
6	1	114	1452	4400	3708	720
7	1	240	5610	32120	58140	33984	5040
8	1	494	19950	195800	644020	785304	341136	40320
9	1	1004	67260	1062500	5765500	12440064	11026296	3733920	362880

''n''번째 행의 합, 즉 $P_n(1)$ 의 값은 $(2n-1)!!$ 이다.

2차 오일러 수의 인덱싱은 세 가지 방식으로 제공된다.

Riordan과 Comtet를 따름
Graham, Knuth 및 Patashnik을 따름
, Gessel과 Stanley의 정의를 확장

참조

_[1] 서적 1974
_[2] 서적 Concrete Mathematics
_[3] 학술 논문 Studien über die Bernoullischen und Eulerschen Zahlen https://eudml.org/do[...] 1883
_[4] 학술 논문 Explicit formulas and recurrence relations for higher order Eulerian polynomials 2017-08-01
_[5] 서적 1755

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com