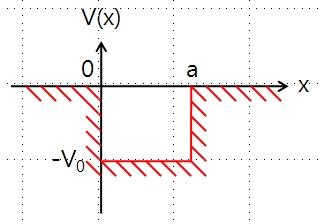
유한 퍼텐셜 우물

3. 유도

시간에 무관한 슈뢰딩거 방정식을 풀면 입자가 유한 퍼텐셜 우물 속에 있을 때의 현상을 살펴볼 수 있다. 1차원적인 경우, 즉 ''x'' 축에 대한 시간에 무관한 슈뢰딩거 방정식은 다음과 같다.^[1]

:$$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\}\{d\; x^2\}\; +\; V(x)\; \backslash psi\; =\; E\; \backslash psi$$

여기서

• $\backslash hbar$는 환원 플랑크 상수이고,
• $m$는 입자의 질량이며,
• $V(x)$는 각 지점 ''x''에서의 퍼텐셜 에너지이고,
• $\backslash psi$는 파동 함수이며,
• $E$는 에너지이다.

\psi_3, & \text{if }x>L/2\text{ (우물 밖 영역)}

\end{cases}

상자 내부 영역에서, ''V''(''x'') = 0이고, 위 식은 다음과 같이 간단해진다.

:$$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\_2\}\{d\; x^2\}\; =\; E\; \backslash psi\_2,$$

이는 시간 독립 자유 슈뢰딩거 방정식과 ''유사''하며, 따라서

:$$E\; =\; \backslash frac\{k^2\; \backslash hbar^2\}\{2m\}\; .$$

다음과 같이 정의하면

:$$k\; =\; \backslash frac\{\backslash sqrt\{2mE\}\}\{\backslash hbar\},$$

방정식은 다음과 같이 된다.

:$$\backslash frac\{d^2\; \backslash psi\_2\}\{d\; x^2\}\; =\; -k^2\; \backslash psi\_2\; .$$

일반적인 해는 다음과 같다.

:$$\backslash psi\_2\; =\; A\; \backslash sin(kx)\; +\; B\; \backslash cos(kx)\backslash ,\; .$$

여기서 ''A''와 ''B''는 임의의 복소수가 될 수 있고, ''k''는 임의의 실수일 수 있다.

상자 외부 영역의 경우, 퍼텐셜이 일정하므로 $V(x)\; =\; V\_0$이고, 위 식은 다음과 같이 된다.

:$$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\_1\}\{d\; x^2\}\; =\; (\; E\; -\; V\_0)\; \backslash psi\_1$$

$E$가 $V\_0$보다 작은지(, 입자가 속박 상태) 또는 큰지($E\; >\; V\_0$, 입자가 비속박 상태)에 따라 두 가지 가능한 해 집합이 있다.

인 속박 상태를 분석해보면, $$\backslash alpha\; =\; \backslash frac\{\backslash sqrt\{2m(V\_0\; -\; E)\}\}\{\backslash hbar\}$$를 사용하면,

:$$\backslash frac\{d^2\; \backslash psi\_1\}\{d\; x^2\}\; =\; \backslash alpha^2\; \backslash psi\_1$$

여기서 일반 해는 지수 함수이다.

:$$\backslash psi\_1\; =\; Fe^\{-\; \backslash alpha\; x\}+\; Ge^\{\; \backslash alpha\; x\}$$

마찬가지로 상자 외부의 다른 영역에 대해:

:$$\backslash psi\_3\; =\; He^\{-\; \backslash alpha\; x\}+\; Ie^\{\; \backslash alpha\; x\}$$

이제 이 문제에 대한 특정 해를 찾기 위해, 적절한 경계 조건을 찾아야 한다. 슈뢰딩거 방정식의 해는 연속적이고 연속적으로 미분 가능해야 한다.^[2]

유한 퍼텐셜 우물은 대칭이므로 대칭성을 활용하여 필요한 계산을 줄일 수 있다. $x$가 $-\backslash infty$로 갈 때 $F$ 항, $x$가 $+\backslash infty$로 갈 때 $I$ 항이 무한대로 가므로, 파동 함수가 제곱 적분 가능하게 하려면 $F\; =\; I\; =\; 0$으로 설정해야 한다.

:$$\backslash psi\_1\; =\; Ge^\{\; \backslash alpha\; x\}$$ 그리고 $$\backslash psi\_3\; =\; He^\{-\; \backslash alpha\; x\}$$

전체 $\backslash psi$ 함수는 연속적이고 미분 가능해야 하므로, 함수 값과 그 도함수는 분할점에서 일치해야 한다.

$\backslash psi\_1(-L/2)\; =\; \backslash psi\_2(-L/2)$		$\backslash psi\_2(L/2)\; =\; \backslash psi\_3(L/2)$
\left.\frac{d\psi_1}{dx}\right>_{x=-L/2} = \left.\frac{d\psi_2}{dx}\right|_{x=-L/2}		\left.\frac{d\psi_2}{dx}\right>_{x=L/2} = \left.\frac{d\psi_3}{dx}\right|_{x=L/2}

이러한 방정식에는 두 가지 종류의 해가 있는데, 대칭적인 경우 $A\; =\; 0$이고 $G\; =\; H$이며, 반대칭적인 경우에는 $B\; =\; 0$이고 $G=-H$이다. 대칭적인 경우

:$$He^\{-\; \backslash alpha\; L/2\}\; =\; B\; \backslash cos(k\; L/2)$$

:$$-\; \backslash alpha\; He^\{-\; \backslash alpha\; L/2\}\; =\; -\; k\; B\; \backslash sin(k\; L/2)$$

따라서 비율을 계산하면

:$$\backslash alpha=k\; \backslash tan(k\; L/2)\; .$$

마찬가지로 반대칭적인 경우에는

:$$\backslash alpha=-k\; \backslash cot(k\; L/2)\; .$$

$\backslash alpha$와 $k$ 둘 다 에너지에 의존한다. 연속성 조건은 임의의 에너지 값에 대해 ''충족될 수 없다''. 이는 무한 퍼텐셜 우물의 결과이기 때문이다. 따라서 이러한 두 방정식 중 하나 또는 둘 다의 해인 특정 에너지 값만 허용된다. 즉, $V\_0$ 미만의 시스템의 에너지 준위는 이산적이며, 해당 고유 함수는 ''결합 상태''임을 알 수 있다. (반대로, $V\_0$ 위의 에너지 준위는 연속적이다.^[3])

에너지 방정식은 해석적으로 풀 수 없지만, 대칭적인 경우 우물이 매우 얕더라도 항상 최소한 하나의 결합 상태가 존재한다.^[4]

무차원 변수 $u=\backslash alpha\; L/2$ 및 $v=k\; L/2$를 도입하고, $\backslash alpha$와 $k$의 정의로부터 $u^2\; =\; u\_0^2-v^2$라는 것을 알 수 있다. 여기서 $u\_0^2=m\; L^2\; V\_0/2\; \backslash hbar^2$이고, 기본 방정식은 다음과 같다.

:$$\backslash sqrt\{u\_0^2-v^2\}\; =\; \backslash begin\{cases\}$$

v \tan v, & \text{(대칭적인 경우) } \\

• v \cot v, & \text{(반대칭적인 경우) }

\end{cases}

$u\_0^2=20$인 경우, 파란색 반원이 보라색 또는 회색 곡선($v\; \backslash tan\; v$ 및 $-v\; \backslash cot\; v$)과 교차하는 곳에 해가 존재한다. 각 보라색 또는 회색 곡선은 가능한 해 $v\_j$를 나타내며, 범위는 이다. 따라서 전체 해의 수 $N$(파란색 원과 교차하는 보라색/회색 곡선의 수)는 파란색 원의 반경 $u\_0$를 각 해의 범위 $\backslash pi/2$로 나누고 바닥 또는 천장 함수를 사용하여 결정된다.^[6]

:$$N\; =\; \backslash left\backslash lfloor\backslash frac\{2u\_0\}\{\backslash pi\}\backslash right\backslash rfloor+1=\backslash left\backslash lceil\backslash frac\{2u\_0\}\{\backslash pi\}\backslash right\backslash rceil$$

$v\_1\; =1.28,\; v\_2=2.54$ 및 $v\_3=3.73$이며, 해당 에너지는 다음과 같다.

:$$E\_n=\{2\backslash hbar^2\; v\_n^2\backslash over\; m\; L^2\}\; .$$

원한다면 방정식에서 상수 $A,\; B,\; G,\; H$의 값을 찾을 수 있다(정규화 조건도 부과해야 한다).

특별한 경우로, 퍼텐셜의 높이가 커지면($V\_0\backslash to\backslash infty$) 근이 값 $v\_n=n\backslash pi/2$에 점점 더 가까워지며, 무한 사각 우물의 경우를 복구한다.

다른 경우는 매우 좁고 깊은 우물($V\_0\backslash to\backslash infty$이고 $L\backslash to\; 0$이며 $V\_0\; L$이 고정)의 경우이다. $u\_0\backslash propto\; \backslash sqrt\{V\_0\}\; L$이므로 0으로 경향, 결합 상태는 하나만 존재한다. 대략적인 해는 $v^2\; =\; u\_0^2\; -\; u\_0^4$이고, 에너지는 $E=-m\; L^2\; V\_0^2/2\backslash hbar^2$로 경향한다. 이는 강도 $V\_0\; L$의 델타 함수 퍼텐셜의 결합 상태의 에너지와 같다.

3. 1. 속박 상태 (E < V₀)

슈뢰딩거 방정식의 해는 연속적이고 미분 가능해야 한다.^[2] 이러한 조건을 만족하는 에너지 준위는 불연속적(양자화)이다. 인 속박 상태에 대해 자세히 알아보자.

먼저 파동 함수를 다음과 같이 설정한다.

:$\backslash psi\; =$

\begin{cases}

\psi_1, & \mbox{if }x<0\mbox{ (우물 밖)} \\

\psi_2, & \mbox{if }0
\psi_3 & \mbox{if }x>a\mbox{ (우물 밖)}

\end{cases}



각 영역에서 슈뢰딩거 방정식을 풀면 다음과 같다.

:$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\_1\}\{d\; x^2\}\; =\; E\; \backslash psi\_1$

:$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\_2\}\{d\; x^2\}\; -V\_0\; \backslash psi\_2\; =\; E\; \backslash psi\_2$

:$-\backslash frac\{\backslash hbar^2\}\{2\; m\}\; \backslash frac\{d^2\; \backslash psi\_3\}\{d\; x^2\}\; =\; E\; \backslash psi\_3$

여기서 $k=\backslash frac\{\backslash sqrt\{2m(E+V\_0)\}\}\{\backslash hbar\}$, $q=\backslash frac\{\backslash sqrt\{-2mE\}\}\{\backslash hbar\}$라고 놓으면 각 영역의 해는 다음과 같다.

:$$

\begin{align}

\psi_1(x)&=e^{qx}\\

\psi_2(x)&=Ae^{ikx}+ Be^{-ikx}\\

\psi_3(x)&=Ce^{-qx}

\end{align}



$x=0$과 $x=a$에서 $\backslash scriptstyle\; \backslash psi\backslash quad$ 와 $\backslash scriptstyle\; \backslash frac\{d\; \backslash psi\}\{dx\}\backslash quad$ 가 연속이라는 경계 조건을 적용하면 다음과 같은 방정식을 얻는다.

:$$

\begin{align}

1&=A+B\\

q&=ik(A-B)\\

Ae^{ika}+Be^{-ika}&=Ce^{-qa}\\

ik(Ae^{ika}-Be^{-ika})&=-qCe^{-qa}

\end{align}



이 연립방정식을 풀면 계수 $A,\; B,\; C$를 구할 수 있다.

:$$

\begin{align}

A&=\frac{1}{2}\left(1-i\frac{q}{k}\right)=B^*\\

B&=\frac{1}{2}\left(1+i\frac{q}{k}\right)\\

C&=\frac{1}{2}e^{qa}\left(\frac{k}{q}+\frac{q}{k}\right)\sin{ka}

\end{align}



경계 조건을 정리하면 다음 식을 얻는다.

:$ka=(n-1)\backslash pi+2\backslash cos^\{-1\}\{\backslash sqrt\{1+\backslash frac\{E\}\{V\_0\}\}\}\backslash \; (n=1,2,3,4,...)$

이 식과 $k=\backslash frac\{\backslash sqrt\{2m(E+V\_0)\}\}\{\backslash hbar\}$을 그래프로 나타내면 속박 상태를 확인할 수 있다. 그래프의 교점으로부터 속박 상태의 에너지를 구할 수 있다.

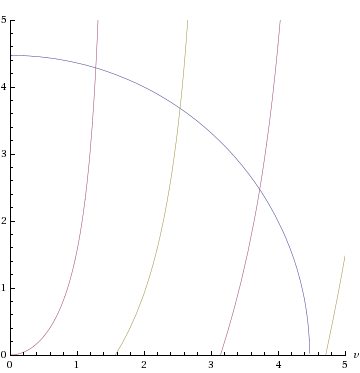
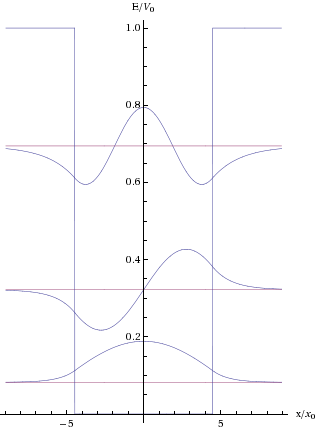
결론적으로, 에너지 준위는 불연속적이며, 이는 양자화된 값을 갖는다는 것을 의미한다.^[3] 우물이 매우 얕거나 좁더라도 최소한 하나의 결합 상태가 항상 존재한다.^[4]

3. 2. 비속박 상태 (E > V₀)

Schrödinger equation|슈뢰딩거 방정식^영어을 에너지 에 대해 풀면, 를 사용하여,

:$\backslash frac\{d^2\; \backslash psi\_1\}\{d\; x^2\}\; =\; -k\text{'}^2\; \backslash psi\_1$

를 얻는다. 그러면 해는 우물 내부의 경우와 동일한 형태를 갖는다.

:$\backslash psi\_1\; =\; C\; \backslash sin(k\text{'}\; x)\; +\; D\; \backslash cos(k\text{'}\; x)$

따라서 우물 내부와 외부 모두에서 진동한다. 해는 절대 제곱 적분 가능하지 않으므로, 항상 정규화할 수 없는 상태이다. 그러나 이것이 양자 입자가 보다 큰 에너지를 갖는 것이 불가능하다는 것을 의미하지는 않으며, 단순히 시스템이 위에 연속 스펙트럼을 갖는다는 것을 의미한다. 즉, 정규화할 수 없는 상태는 여전히 비유계 연산자의 일반화된 고유 함수로 스펙트럼의 연속 부분에 기여한다.^[1]

4. 비대칭 유한 퍼텐셜 우물

다음과 같은 퍼텐셜을 갖는 1차원 비대칭 퍼텐셜 우물을 생각해 보자.^[8]

:$$V(x)\; =\; \backslash begin\{cases\}$$

V_1, & \text{if }-\infty
0, & \text{if }0
V_2 & \text{if }a
\end{cases}

여기서 $V\_2\; >\; V\_1$이다.

:$$\backslash psi(x)\; =\; \backslash begin\{cases\}$$

c_1 e^{k_1 x}, & \text{for }x<0, \text{where } k_1 = \sqrt{(2m/\hbar^2)(V_1-E)} \\

c\sin(kx+\delta), & \text{for }0
c_2 e^{-k_2 x}, & \text{for }x>a, \text{where } k_2 = \sqrt{(2m/\hbar^2)(V_2-E)}

\end{cases}

그리고

:$$\backslash sin\backslash delta\; =\; \backslash frac\{k\backslash hbar\}\{\backslash sqrt\{2mV\_1\}\}.$$

에너지 준위 $E=k^2\backslash hbar^2/(2m)$는 $k$가 다음 초월 방정식의 근으로 풀리면 결정된다.

:$$ka\; =\; n\backslash pi\; -\; \backslash sin^\{-1\}\backslash left(\backslash frac\{k\backslash hbar\}\{\backslash sqrt\{2mV\_1\}\}\backslash right)\; -\; \backslash sin^\{-1\}\backslash left(\backslash frac\{k\backslash hbar\}\{\backslash sqrt\{2mV\_2\}\}\backslash right)$$

여기서 $n=1,2,3,\backslash dots$이다. 위의 방정식의 근이 항상 존재하는 것은 아니다. 예를 들어, 주어진 $V\_1$과 $V\_2$의 값에 대해 이산 에너지 준위가 존재하지 않도록 $a$의 값을 항상 작게 만들 수 있다. 대칭 우물의 결과는 $V\_1\; =\; V\_2\; =\; V\_o$로 설정하여 위의 방정식으로부터 얻어진다.

5. 구형 유한 퍼텐셜 우물

다음과 같은 구형 퍼텐셜 우물을 고려해 볼 수 있다.

:$$U(r)\; =\; \backslash begin\{cases\}$$

• U_0, & \text{if }r

5. 1. 속박 상태의 존재 조건

6. 구형 대칭 고리형 우물

위의 결과는 1차원적인 경우처럼 구형 공동에서 두 개의 속박 상태가 존재한다는 것을 보여준다. 왜냐하면 구 좌표계는 모든 방향에서 반경을 동일하게 만들기 때문이다.

구 대칭 퍼텐셜의 바닥 상태 (''n'' = 1)는 항상 궤도 각운동량 0 (ℓ = n−1)을 가지며, 축소된 파동 함수 $\backslash chi(r)\; \backslash equiv\; r\backslash psi\; (r)$는 다음 방정식을 만족한다.

:$$-\backslash frac\; \{\backslash hbar\; ^2\}\{2m\}\; \backslash frac\; \{d^2\; \backslash chi\}\{dr^2\}\; +\; U(r)\; \backslash chi(r)\; =\; E\backslash chi(r)$$

여기서 $\backslash psi\; (r)$는 파동 함수의 방사 부분이다. (''n'' = 1)일 때 각 부분은 상수 (''ℓ'' = 0)임을 주목하라.

이것은 경계 조건을 제외하면 1차원 방정식과 동일하다. 이전과 마찬가지로,

:$$\backslash chi\; (r)\; =\; \backslash begin\{cases\}$$

c_1 \sin({k_1 r}), & \text{for } r < a, \text{ where } k_1 = \sqrt {2m / \hbar^2 (U_{1}-E)} \\[1ex]

c \sin({kr + \delta}), & \text{for } a < r < b, \text{ where } k = \sqrt {2mE / \hbar ^2} \\[1ex]

c_2 e^{-k_2 r}, & \text{for } r > b, \text{ where } k_2 = \sqrt {2m / \hbar ^2 (U_2-E)}

\end{cases}





:$$E\; =\; \backslash frac\{k^2\; \backslash hbar\; ^2\}\{2m\}$$

는 $\{\backslash displaystyle\; k\}$가 다음 초월 방정식의 근으로 풀리면 결정된다.

:$$k(b-a)\; =\; n\backslash pi$$

여기서 $\{\backslash displaystyle\; n=1,2,3,\backslash dots\; \}$

위 방정식의 근의 존재는 항상 보장된다. 결과는 항상 구 대칭성을 가진다. 파동이 구 내부에서 어떠한 퍼텐셜도 찾지 못하는 조건 $\backslash chi(a)\; =\; \backslash chi(0)=\; 0$을 충족한다.

ℓ ≠0일 때는 다른 미분 방정식이 놓이므로 위의 제목과 같이 다음과 같다.

: $\backslash frac\; \{d^2\; \backslash chi\}\{dr^2\}\; +\; \backslash begin\{Bmatrix\}\; k^2-\backslash frac\{l(l+1)\}\{r^2\}\; \backslash end\{Bmatrix\}\; \backslash chi(r)\; =\; 0$

해는 몇 가지 변수와 함수의 변경을 통해 베셀과 같은 미분 방정식을 얻을 수 있으며, 그 해는 다음과 같다.

:$\backslash frac\; \{\backslash chi\; (r)\}\{r\}\; =\; \backslash begin\{cases\}$

A j_l({k_1 r}), & \text{for } r < a, \text{ where } k_1 = \sqrt {2m / \hbar^2 (U_{1}-E)} \\[1ex]

A j_l({kr})+B y_l({kr}), & \text{for } a < r < b, \text{ where } k = \sqrt {2mE / \hbar ^2} \\[1ex]

C h_l^{(1)}({k_2r}), & \text{for } r > b, \text{ where } k_2 = \sqrt {2m / \hbar ^2 (U_2-E)}

\end{cases}



여기서 $j\_l\; \{(kr)\}$, $y\_l\; (\{kr\})$ 및 $h\_l^\{(1)\}(\{kr\})$는 각각 베셀, 뉴만 및 헹켈 구 함수이며, 표준 베셀 함수의 함수로 다시 작성할 수 있다.



:$$E\; =\; \backslash frac\{k^2\; \backslash hbar\; ^2\}\{2m\}$$



는 $\{\backslash displaystyle\; k\}$가 다음 초월 방정식의 근으로 풀리면 결정된다.

:$$k(b-a)\; =\; \backslash frac\; \{4n\backslash pi\}\{2\backslash ell+1\}$$

여기서 $\{\backslash displaystyle\; n=1,2,3,\backslash dots\; \}$

또한 이 두 개의 초월 방정식은 $\{\backslash displaystyle\; k\}$ 해이다.

:$$kb\; =\; \backslash frac\; \{n\backslash pi\}\{2\backslash ell+1\}\backslash begin\{Bmatrix\}3-2\backslash sin^2\; \backslash left(\backslash pi\backslash frac\{\backslash ell+1\}\{2\}\backslash right)\backslash end\{Bmatrix\}$$ 그리고,

:$$ka\; =\; \backslash frac\; \{n\backslash pi\}\{2\backslash ell+1\}\backslash begin\{Bmatrix\}3-2\backslash sin^2\; \backslash left(\backslash pi\backslash frac\{\backslash ell+1\}\{2\}\backslash right)\backslash end\{Bmatrix\}$$

위 방정식의 근의 존재는 항상 보장된다. 결과는 항상 구 대칭성을 가진다.

7. 응용

양자점(Quantum Dot), 양자 우물(Quantum well), 초격자(Superlattice)와 같은 구조를 갖는 계는 유한 퍼텐셜 우물의 관점에서 물리적인 현상을 설명할 수 있다.^[1]

참조

_[1] 서적
_[2] 서적
_[3] 서적
_[4] 서적
_[5] 논문 A simpler graphical solution and an approximate formula for energy eigenvalues in finite square quantum wells 2020
_[6] 서적 Topics in Quantum Mechanics https://books.google[...] Springer Science+Business Media
_[7] 간행물 A chart for the energy levels of the square quantum well 2016
_[8] 서적 Quantum mechanics: non-relativistic theory Elsevier 2013
_[9] 서적 Quantum Mechanics, Selected Topics World Scientific 1998