이항 힙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

이항 힙은 이항 트리의 집합으로 구성된 자료구조로, 최소 힙 속성을 만족하며 각 차수마다 최대 하나의 이항 트리를 가질 수 있다. 이항 힙은 힙의 병합, 삽입, 최소값 찾기, 최소값 삭제, 키 값 감소, 삭제 등의 연산을 지원하며, 각 연산은 O(log n)의 시간 복잡도를 가진다. 이항 힙은 우선순위 큐 및 이산 사건 시뮬레이션 등 다양한 분야에서 활용되며, 이진 힙, 피보나치 힙 등 다른 힙 자료 구조와 비교하여 장단점을 갖는다.

더 읽어볼만한 페이지

힙 - 힙 (자료 구조)
힙은 이진 트리 기반의 자료구조로, 부모 노드의 키 값이 자식 노드보다 크거나 작도록 구성되며, 최대 힙과 최소 힙이 존재하고, 배열로 구현되어 삽입, 삭제 연산의 시간 복잡도는 O(log n)이며, 다양한 분야에 활용된다.
힙 - 이진 힙
이진 힙은 완전 이진 트리 기반 자료 구조로 우선순위 큐 구현에 사용되며, 힙 속성을 유지하기 위해 삽입/제거 시 상향 또는 하향 힙 연산을 수행하고 배열로 효율적인 구현이 가능하다.

이항 힙

2. 이항 트리

이항 힙은 '''이항 트리'''의 집합으로 구성된다. 이항 트리는 다음과 같이 재귀적으로 정의된다.^[1]

이름은 모양에서 비롯되었다. 차수 $k$ 의 이항 트리는 깊이 $d$ 에 $\tbinom k d$ 개의 노드를 갖는다. 이는 이항 계수이다.

2. 1. 이항 트리의 정의

차수가 0인 이항 트리는 하나의 노드이다.
차수가 k인 이항 트리는 루트 노드를 가지며, 루트 노드의 자식은 각각 차수가 k-1, k-2, ..., 2, 1, 0인 이항 트리이다.

Order가 0부터 3인 이항 트리: 각 트리는 루트 노드와 하위 트리(subtree)로 구성되는데, 이때 하위 트리는 자신보다 order가 낮은 모든 이항 트리가 하위 트리가 된다. 그림에서 강조하여 표현된 것이 하위 트리들이다. 예를 들어, order가 3인 이항 트리는 order가 2, 1, 0 인 이항 트리(각각 파란색, 녹색, 붉은색으로 표시함)와 연결되어 있다.

Order가 k인 이항 트리는 2^k개의 노드를 가졌으며, 트리의 높이는 k이다.

이러한 특이한 구조 때문에, order가 k인 이항 트리는 order가 k-1인 두 개의 트리를 가지고 쉽게 구성할 수 있다. 즉, 하나의 트리(order가 k-1인 트리)의 루트 노드의 가장 왼쪽에, 나머지 하나의 트리(order가 k-1인 또다른 트리)를 자식 노드로 붙이면 간단히 만들어진다. 이러한 특성은 이항 힙 merge 연산의 중심 개념이 되는데, 다른 일반 힙에 비해 이항 힙이 가진 주요한 장점이라 하겠다.

2. 2. 이항 트리의 특징

차수가 k인 이항 트리는 2^k개의 노드를 가지며, 트리의 높이는 k이다.^[1] 이러한 구조 덕분에, 차수가 k인 이항 트리는 차수가 k-1인 두 개의 트리를 이용하여 쉽게 구성할 수 있다. 즉, 하나의 트리 (차수가 k-1인 트리)의 루트 노드의 가장 왼쪽에, 나머지 하나의 트리 (order가 k-1인 또 다른 트리)를 자식 노드로 붙이면 간단히 만들어진다.^[1]^[3] 이러한 특성은 이항 힙의 병합(merge) 연산의 핵심 개념이며, 다른 일반 힙에 비해 이항 힙이 가진 주요한 장점이다.

이름은 모양에서 비롯되었다. order가 n인 이항 트리는 깊이(depth) d에서 (n¦d)의 노드를 가진다. (이항 계수 참조)

3. 이항 힙의 구조

이항 힙은 다음 두 가지 속성을 만족하는 이항 트리의 집합이다.^[1]

힙을 구성하는 각 이항 트리는 최소 힙 속성을 따른다. 즉, 노드의 키는 자신의 부모 노드의 키 값보다 크거나 같다.
0 차수를 포함하여 각 차수별로 1개 또는 0개의 이항 트리가 있을 수 있다.

첫 번째 특성은 각 이항 트리의 루트가 트리에서 가장 작은 키를 포함할 것을 보장하며, 이는 전체 힙에 적용된다. 두 번째 특성은 n개의 노드를 가지는 이항 힙은 많아야 log n + 1개의 이항 트리로 구성된다는 것을 의미한다.

3. 1. 최소 힙 속성

이항 힙을 구성하는 각 이항 트리는 '''최소 힙 속성'''을 만족한다. 즉, 노드의 키 값은 자신의 부모 노드의 키 값보다 크거나 같다.^[1] 이 속성은 각 이항 트리의 루트가 해당 트리에서 가장 작은 키 값을 갖도록 보장하며, 이는 전체 힙에도 적용된다.

3. 2. 차수 제약 조건

이항 힙은 각 차수에 대해 최대 하나의 이항 트리만 가질 수 있다는 제약 조건을 갖는다. 즉, 동일한 차수의 이항 트리가 두 개 이상 존재할 수 없다.^[1]

이러한 특성으로 인해,

n

개의 노드를 가진 이항 힙은 최대

1+\log_2 n

개의 이항 트리로 구성된다. 여기서

\log_2

는 이진 로그이다. 각 이항 트리는 숫자

n

의 이진법 표현에서 0이 아닌 각 비트에 대응된다. 예를 들어, 십진수 13은 이진수로 1101(

2^3 + 2^2 + 2^0

)이므로, 13개의 노드를 가진 이항 힙은 3, 2, 0 차수의 세 개의 이항 트리로 구성된다.^[1]^[3]

3. 3. 노드 개수와 이항 트리의 관계

n^영어개의 노드를 가지는 이항 힙은 최대 log n + 1^영어개의 이항 트리로 구성된다. 각 이항 트리는 n^영어의 이진수 표현에서 1에 해당한다. 예를 들어, 13(이진수: 1101)개의 노드를 가진 이항 힙은 차수가 각각 3, 2, 0인 세 개의 이항 트리로 구성된다.^[1]^[3]

4. 이항 힙의 연산

이항 힙은 여러 개의 이항 트리로 구성된 자료 구조이며, 각 이항 트리는 최소 힙 속성을 만족한다. 이항 힙의 연산은 이러한 특성을 이용하여 효율적으로 수행된다.

이항 힙의 주요 연산에는 다음이 있다.

병합 (Merge): 두 개의 이항 힙을 하나로 합친다.
삽입 (Insert): 새로운 요소를 힙에 추가한다.
최소값 찾기 (Find Minimum): 힙에서 가장 작은 값을 가진 요소를 찾는다.
최소값 삭제 (Delete Minimum): 힙에서 가장 작은 값을 가진 요소를 삭제한다.
키 값 감소 (Decrease Key): 특정 요소의 키 값을 감소시킨다.
삭제 (Delete): 힙에서 특정 요소를 삭제한다.

4. 1. 병합 (Merge)

두 개의 이항 힙을 병합하는 연산은 이항 힙에서 가장 중요하며, 다른 연산들에서도 자주 사용된다. 이 연산은 동일한 차수의 두 이항 트리를 병합하는 과정을 기반으로 한다.

두 이항 트리의 루트 노드 중 키 값이 작은 것을 새로운 루트 노드로 선택하고, 키 값이 큰 루트 노드를 가진 트리를 작은 키 값을 가진 트리의 자식 트리로 연결한다. 이렇게 하면 두 개의 이항 트리가 하나의 더 큰 차수의 이항 트리로 병합된다.

두 이항 힙을 병합하기 위해서는, 두 힙의 루트 리스트를 병합 정렬과 유사하게 작은 차수부터 큰 차수 순서로 함께 살펴본다. 만약 두 힙 중 하나의 힙에만 특정 차수의 트리가 있다면, 그 트리는 그대로 결과 힙으로 이동한다. 만약 두 힙 모두에 특정 차수의 트리가 있다면, 두 트리를 위에서 설명한 방식으로 병합하여 차수가 하나 더 큰 트리로 만든다. 이 때, 새로 만들어진 트리가 다른 트리와 다시 병합되어야 할 수도 있다.

이 과정에서 어떤 차수의 트리를 최대 세 개까지 검사하게 된다. (원래 두 힙에서 각각 하나씩, 그리고 두 개의 작은 트리가 병합되어 만들어진 트리 하나).

4. 1. 1. 병합 연산의 시간 복잡도

각 이항 트리의 차수는 최대 log₂ ''n''^영어이므로, 병합 연산의 실행 시간은 O(log ''n'')^영어이다.^[1]^[3]

4. 2. 삽입 (Insert)

새로운 요소를 힙에 삽입하는 연산은, 삽입하려는 요소를 포함한 힙을 새로 생성한 후, 이 힙을 기존의 힙과 병합함으로써 간단히 수행할 수 있다. 병합 연산 때문에 O(log n)만큼의 시간이 소요된다. 그러나, 일련의 삽입 연산을 연속적으로 n번 수행하는 경우 삽입은 O(1)의 분할상환 시간을 가진다(O(1)이라 함은 상수만큼의 시간이 걸린다는 의미).^[1]^[3]

스큐 이항 힙은 트리의 크기가 이진수 체계가 아닌 스큐 이진수 체계를 기반으로 하는 포레스트를 사용하여 최악의 경우 상수 시간 삽입 시간을 달성한다.^[4]

4. 3. 최소값 찾기 (Find Minimum)

이항 힙에서 최소값을 찾으려면, 이항 트리의 루트들 중에서 최소값을 찾으면 된다. 힙 안에는 최대 O|오^영어(log ''n'')개의 트리가 존재하므로, 최소값 찾기 연산은 O|오^영어(log ''n'') 시간 안에 수행할 수 있다.^[1]

최소값 요소를 포함하는 이항 트리를 가리키는 포인터를 사용하면, 이 연산 시간을 O|오^영어(1)로 줄일 수 있다. 이 포인터는 최소값 찾기 외의 다른 연산을 수행할 때 반드시 업데이트해야 한다. 업데이트는 각 연산의 실행 시간에 O|오^영어(log ''n'') 시간을 더하지만, 전체 시간 복잡도를 증가시키지는 않는다.

4. 4. 최소값 삭제 (Delete Minimum)

힙에서 최소값을 가지는 구성요소를 삭제하려면, 먼저 해당 구성요소를 찾고, 이 구성요소가 들어 있는 이항 트리에서 이 구성요소를 삭제한 후, 이것의 하위 트리 리스트를 구한다. 그리고 나서 이 하위 트리 리스트를 이항 힙으로 변환하는데, 이것은 가장 작은 것부터 가장 큰 것 순으로 순서를 재배치하여 수행한다. 그러고 나서 이 힙을 기존의 힙에 병합한다.^[1] 이 트리는 많아야 log n^영어개의 자식을 가지기 때문에, 새로운 힙을 생성하는데 걸리는 시간은 O(log n^영어)이다. 또한 힙을 병합하는데 O(log n^영어)의 시간이 걸리므로, 최소값 삭제 연산 전체에 걸리는 시간은 O(log n^영어)이다.^[1]

아래는 최소값 삭제 연산의 의사 코드이다.

:min = heap.trees().first()

:'''for each''' current '''in''' heap.trees()

::'''if''' current.root < min.root '''then''' min = current

:'''for each''' tree '''in''' min.subTrees()

::tmp.addTree(tree)

:heap.removeTree(min)

:merge(heap, tmp)

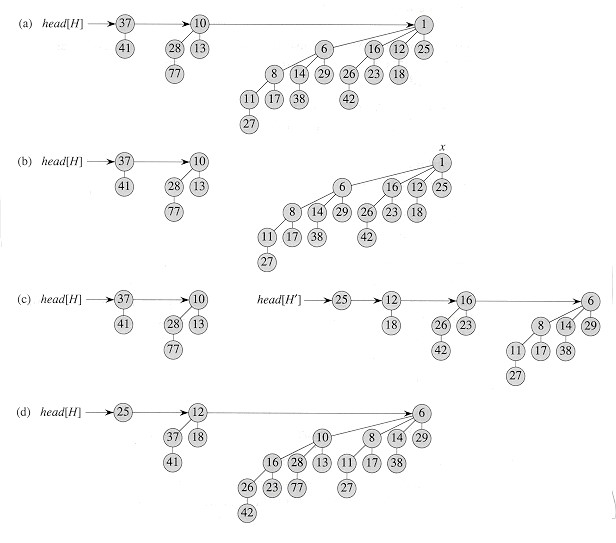
힙에서 최소값 요소를 삭제하려면, 먼저 삭제할 요소를 검색하고, 이항 트리에서 해당 요소를 삭제한 후, 해당 요소를 삭제한 이항 트리의 부분 트리 목록을 얻는다. 이때, 분리된 이항 힙 내에 있는 부분 트리의 목록을 크기 순으로 정렬한다. 그런 다음 해당 힙과 원래의 힙을 병합한다.^[1]

4. 5. 키 값 감소 (Decrease Key)

어떤 요소의 키 값을 감소시킨 후, 그 키 값이 부모의 키 값보다 작아지면 최소 힙 속성이 위반된다. 이런 경우, 해당 원소를 부모와 교환하고, 필요하다면 조부모와도 교환하는 과정을 최소 힙 속성이 유지될 때까지 반복한다. 각 이항 트리의 높이는 최대 log|로그^영어 n이므로, 이 작업은 O(log|로그^영어 n) 시간이 걸린다.^[1] 하지만 이 연산은 트리의 각 노드에서 부모 노드로의 포인터를 포함하는 트리 표현이 필요하며, 이는 다른 연산들의 구현을 다소 복잡하게 만든다.^[3]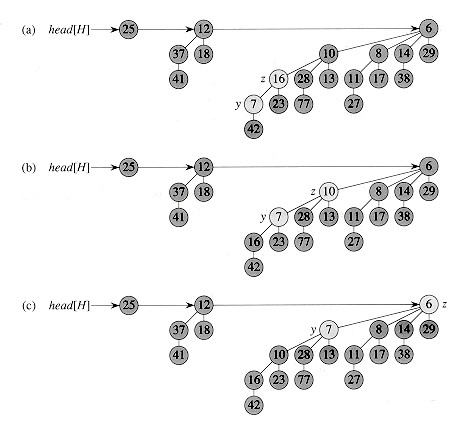

(a)의 y에 해당하는 값을 7로 감소시키면, 부모 키 16보다 작으므로 (b)와 같이 7과 16의 노드가 교환된다. 이 값은 다시 부모 키 10보다 작으므로 (c)와 같이 노드가 한 번 더 교환되어 최종적으로 (c)와 같은 결과가 된다.

4. 6. 삭제 (Delete)

힙에서 특정 요소를 삭제하는 연산은, 해당 요소의 키 값을 음의 무한대로 감소시킨 후,^[1] 최소값 삭제 연산을 수행하는 방식으로 수행된다.

5. 시간 복잡도 요약

다음은 다양한 힙 자료 구조의 시간 복잡도^[5]를 나타낸 표이다. 여기서 ''O''(''f'')" 및 "''Θ''(''f'')"의 의미는 점근 표기법을 참조하며, 연산 이름은 최소 힙을 가정한다.

연산	find-min	delete-min	감소-키	삽입	병합	make-heap
이항^[5]^[9]	Θ(1)	Θ(log n)	Θ(log n)	Θ(1)	Θ(log n)	Θ(n)

''n''개의 요소를 가진 이항 힙에 대해, 다음 모든 연산의 계산량은 ''O''(log n)이다.

힙에 새로운 요소를 삽입
최소 키를 가진 요소 검색
힙에서 최소 키를 가진 요소 삭제
지정된 요소의 키 값 감소
힙에서 특정 요소 삭제
두 개의 임의의 힙을 하나의 힙으로 병합

최소 키를 가진 요소 검색은 최소 키에 대한 포인터를 추가하고 이용함으로써 ''O''(1)로 실행할 수 있다.

6. 응용

우선순위 큐 및 이산 사건 시뮬레이션 등에 응용된다.

7. 파생

피보나치 힙이나 소프트 힙과 같은 다른 유사한 힙 자료 구조를 구축하는 데 이항 힙이 사용된다.

참조

_[1] 서적 Introduction to Algorithms
_[2] 논문 A data structure for manipulating priority queues 1978-04-01
_[3] 논문 Implementation and analysis of binomial queue algorithms
_[4] 간행물 Optimal purely functional priority queues 1996-11
_[5] 서적 Introduction to Algorithms
_[6] 논문 Average Case Analysis of Heap Building by Repeated Insertion http://www.stats.ox.[...] 2016-01-28
_[7] 논문 Self-Adjusting Heaps https://www.cs.cmu.e[...] 1986-02
_[8] 서적 Data Structures and Network Algorithms
_[9] 웹사이트 Binomial Heap {{!}} Brilliant Math & Science Wiki https://brilliant.or[...] 2019-09-30
_[10] 간행물 Optimal purely functional priority queues 1996-11
_[11] 서적 Purely Functional Data Structures
_[12] 간행물 Theory of 2–3 Heaps https://ir.canterbur[...]
_[13] 간행물 Proc. 7th Scandinavian Workshop on Algorithm Theory http://john2.poly.ed[...] Springer-Verlag
_[14] 논문 On the Efficiency of Pairing Heaps and Related Data Structures http://www.uqac.ca/a[...] 1999-07
_[15] 간행물 Towards a Final Analysis of Pairing Heaps http://web.eecs.umic[...]
_[16] 논문 Rank-pairing heaps http://sidsen.org/pa[...] 2011-11
_[17] 논문 Fibonacci heaps and their uses in improved network optimization algorithms http://bioinfo.ict.a[...] 1987-07
_[18] 간행물 Strict Fibonacci heaps http://www.cs.au.dk/[...]
_[19] 간행물 Proc. 7th Annual ACM-SIAM Symposium on Discrete Algorithms
_[20] 서적 Data Structures and Algorithms in Java

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com