지오이드
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
지오이드는 지구의 중력장을 나타내는 가상적인 표면으로, 지구의 평균 해수면과 거의 일치하며, 측지학에서 기준면으로 사용된다. 지구 내부의 밀도 차이, 지질학적 구성, 지각의 굴곡 등으로 인해 지오이드의 형태는 불규칙하며, 기준 타원체와의 높이 차이를 지오이드 높이(요동)라고 한다. 지오이드 높이는 GPS 등의 측량에서 사용되며, 표고와 타원체 고도 간의 관계를 통해 계산된다. 지오이드의 형태는 시간적으로 변화하며, 위성 임무를 통해 연구되고 있으며, 구면조화 함수를 사용하여 표현된다.
더 읽어볼만한 페이지
- 측지학 - 위도
위도는 지구 표면의 남북 위치를 각도로 나타내며, 지구를 회전 타원체로 가정했을 때 법선과 적도면이 이루는 각으로 측정하여 적도를 0°로 북극과 남극까지 나타내고, 기후와 지리적 특징 등에 영향을 미치는 다양한 종류가 존재한다. - 측지학 - 측지계
측지계는 지구의 형태와 위치를 수학적으로 모델링하여 위도, 경도, 고도 등을 정의하고 측량, 지도 제작, GPS 등에 활용되는 기준 좌표계이다. - 중력 - 중력 가속도
중력 가속도는 물체가 중력에 의해 가속되는 정도를 나타내는 값으로, 자유 낙하하는 물체의 가속도와 같으며, 지구의 경우 자전에 의한 원심력으로 인해 적도에서 가장 작고 극에서 가장 크게 나타난다. - 중력 - 만유인력의 법칙
만유인력의 법칙은 모든 질량을 가진 물체들이 서로를 끌어당기는 힘에 대한 법칙으로, 뉴턴은 질량에 비례하고 거리의 제곱에 반비례한다는 것을 제시했으며, 케플러의 행성 운동 법칙을 설명하고 뉴턴 역학의 기초가 되었으나, 일반 상대성 이론이 등장하면서 저중력 한계로 여겨진다.
| 지오이드 | |
|---|---|
| 지도 정보 | |
| 개요 | |
| 종류 | 등포텐셜면 |
| 설명 | 지구 중력장에서 평균 해수면과 일치하는 등포텐셜면 |
| 추가 설명 | 지오이드는 바람과 조수를 제외하고 해수면이 유지되는 모양을 뜻함 |
| 정의 및 특징 | |
| 정의 | 중력 포텐셜이 일정한 등포텐셜면 |
| 중요 특징 | 지구의 모양과 중력장을 나타내는 중요한 기준면 수직선 방향과 직교 |
| 다른 설명 | 지구 타원체와는 다른 모양을 가짐 |
| 참고 | 지오이드 높이는 지구 타원체를 기준으로 한 높이를 말함 |
| 응용 | |
| 사용 분야 | 측지학 지도 제작 지구과학 |
| 측지학 | 지오이드를 기준으로 높이를 측정 |
| 지도 제작 | 지도 투영에 기준면으로 사용 |
| 지구과학 | 지구 중력장 연구에 활용 |
| 기타 | |
| 참고 | 지오이드는 지구 타원체와 달리 평평하지 않고 불규칙함 지구 내부 질량 분포에 따라 모양이 변함 |
| 관련 개념 | 지구 타원체 수직선 중력 지오포텐셜 |
| 외부 링크 | NGA: Office of Geomatics (미국 국가 지리 정보국) |
2. 형태
지오이드 면은 굴곡이 심해 측지측량에는 직접 활용할 수 없지만, 준거타원체와 거의 동일한 모양을 가진다.[38] 지구 표면은 에베레스트 산(약 +8,800m)과 마리아나 해구(약 -11,000m)처럼 큰 기복을 보이지만, 지오이드의 타원체로부터의 편차는 +85m(아이슬란드)에서 -106m(인도 남부) 정도로 총 200m 미만이다.[4]
만약 해양이 일정한 밀도를 가지고 조류, 해류 또는 날씨의 영향을 받지 않는다면, 그 표면은 지오이드와 유사할 것이다. 지오이드와 평균 해수면 사이의 영구적인 편차를 해양 표면 지형이라고 한다. 만약 대륙 육지가 일련의 터널이나 운하로 얽혀 있다면, 그 운하의 해수면 또한 지오이드와 거의 일치할 것이다. 측지학자들은 수준측량을 통해 대륙 지점의 지오이드 상의 높이를 구할 수 있다.
등퍼텐셜면인 지오이드는 정의상 중력이 모든 곳에서 수직인 면이며, 일시적인 조석 변동은 제외된다. 배를 타고 여행할 때 지오이드의 요동을 알아채지 못하는 이유는, 조석을 무시하면 국부적인 수직선(추의 연직선)은 항상 지오이드에 수직이고 국부적인 지평선은 지오이드에 접선이기 때문이다. 마찬가지로, 수준기는 항상 지오이드와 평행하다.
지오이드는 지구의 평균 해수면에 일치하는 등지오포텐셜면으로, 지구 중력 이외의 영향을 제거했을 경우 전 지구를 덮는 가상적인 해면에 일치한다. 이 평균 해수면은 육지까지 연장되는데, 운하나 터널을 파서 그 장소까지 해수를 인도했다고 가정한다.[32]
따라서, 지오이드란, 지오포텐셜에 의해 형성되는 일종의 “지구의 모양”을 표현하고 있다.
지구의 지오이드는 지구타원체라고 불리는 회전타원체로 그 모양을 근사할 수 있지만, 정확하게는 세세하고 복잡하게 왜곡된 “배”와 같은 모양을 하고 있으며, 지구타원체 모델 GRS80의 타원체면을 기준으로 최대 약 85m의 돌출과 약 105m의 오목함을 가진다. 이 지오이드면의 상대적 높이(차이)를 “지오이드 높이”라고 부른다.
2. 1. 지오이드의 요동
'''지오이드의 요동'''(undulation of the geoid)은 주어진 기준 타원체에 대한 지오이드의 상대적인 높이를 말한다. 국가마다 다른 평균 해수면을 기준점으로 채택하고 있기 때문에 요동은 표준화되지 않았지만, 가장 일반적으로는 EGM96 지오이드를 가리킨다.[5]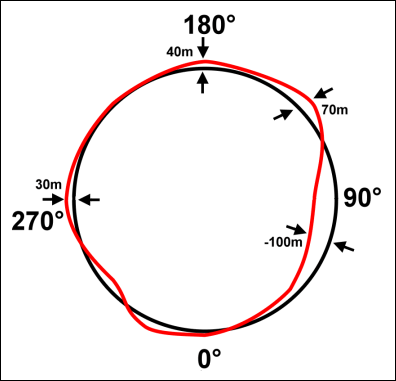
3. 지오포텐셜 기준값
지오이드면은 지구의 평균 해수면과 잘 일치하도록 정규 중력 퍼텐셜 기준값()을 정함으로써 결정된다. 지오포텐셜의 공간 분포에 더하여 지오이드면 상의 점에서는 이다.[32] 국제적으로 GRS80 모델에 의한 값은 이고, 국제지구자전 및 지구기준계측사업(IERS)에서는 를 사용하고 있다.
측량용으로 정하는 지오이드는 의 값을 정하는 것이 아니라, 기준 지점의 평균 해수면을 기반으로 결정하는 경우가 많다.
일본에서는 “일본의 지오이드 2011(GSIGEO2011)”이 측량용으로 정해져 있으며, 도쿄만 평균 해면이 기준이다.
4. 지오이드 면과 평균 해수면
평균해면은 지오포텐셜뿐만 아니라 꾸준한 해류 및 해수온 등의 영향을 받으므로 지오이드면과 최대 2m 정도의 차이가 있다.[32] 이러한 차이를 해양 표면 지형이라고 한다.
5. 지오이드 면과 표고
지오이드는 지구 형상의 기준이 되는 면으로, 항상 연직선(중력이 작용하는 방향)에 수직이다. 지오이드 상의 점에서 지구타원체에 수직인 선분을 지구타원체 표면까지 연장했을 때 그 선분의 길이를 '''지오이드 높이'''라고 한다. 지오이드 상의 점에서 지오이드 면에 수직인 선분을 지표까지 연장했을 때 그 길이를 '''표고'''라고 한다.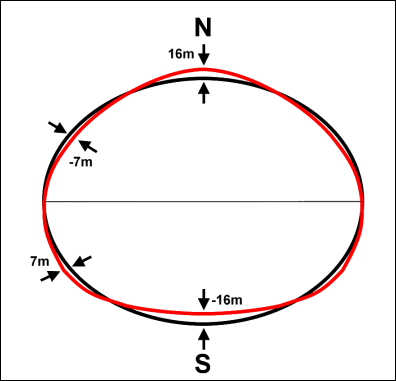
GPS 시스템 및 유사한 GNSS에서 얻어지는 '''타원체 높이'''(''h'')와 정고(평균 해수면)(''H'')를 기준으로 한 높이인 표고의 관계는 다음과 같다.
실제로 많은 휴대용 GPS 수신기는 미리 계산된 ''지오이드 지도''(즉, 검색표)에서 ''N''을 보간한다.[5]
따라서, 지오이드 높이 (''N'') * 표고 (''H'') ≈ 타원체고(''h'') - 지오이드고(''N'') 의 관계를 가진다.[34]
예를 들어, 일본수준원점(위도 35도 40분 37.9899초, 경도 139도 44분 52.2492초)의 지오이드 높이는 36.7071m이며, 그 표고는 24.3900m이므로, 타원체 높이는 61.0971m (36.7071m + 24.3900m)이다.
또한, 이등삼각점 "후지산"(위도 35도 21분 38.2608초, 경도 138도 43분 38.5153초)의 지오이드 높이는 42.5075m이며, 그 표고는 3775.51m이므로[35], 타원체 높이는 3818.02m (42.5075m + 3775.51m)이다.
6. 지오이드 면의 요철
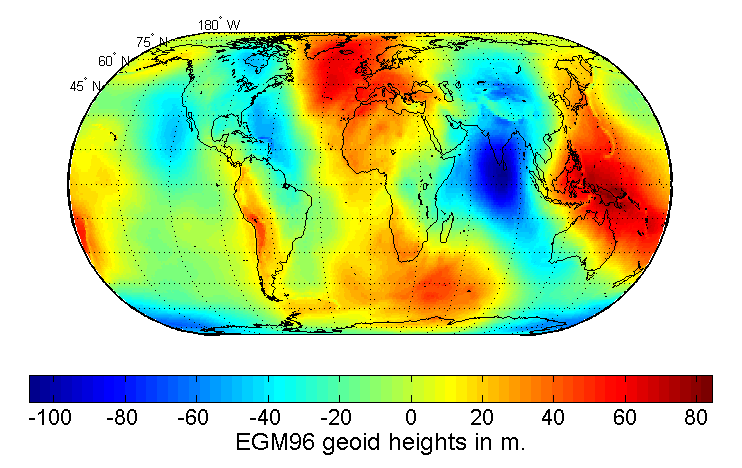
지오이드의 요철은 주변 지형과 지하 암석의 밀도에 영향을 받는다. 산맥이 있거나 평지라도 지하에 밀도가 높은 암석이 있으면 그 주변에서 지오포텐셜이 낮아져 지오이드는 지구타원체 표면보다 돌출한다.
한국의 경우, 중부 지방에서 동북 지방까지의 산간부에서 지오이드가 솟아 있으며, 그 높이는 +40m에서 +50m 정도이다. 서울 근교에서는 +30m 정도이다.[36]
7. 중력 이상과의 관계
지구의 중력장은 균일하지 않다. 편구체가 이상적인 지구로 사용되지만, 행성 전체의 밀도가 다르기 때문에 중력의 세기는 모든 곳에서 동일하지 않다. 이는 마그마 분포, 지질학적 구성의 밀도와 무게 차이, 지각의 산맥, 심해 해구, 빙하로 인한 지각 압축 등 때문이다. 지오이드 수준은 물이 있을 위치와 일치한다. 일반적으로 지구 물질이 국지적으로 더 밀도가 높고, 더 큰 중력을 작용하며, 주변 지역에서 더 많은 물을 끌어당길 때 지오이드가 상승한다.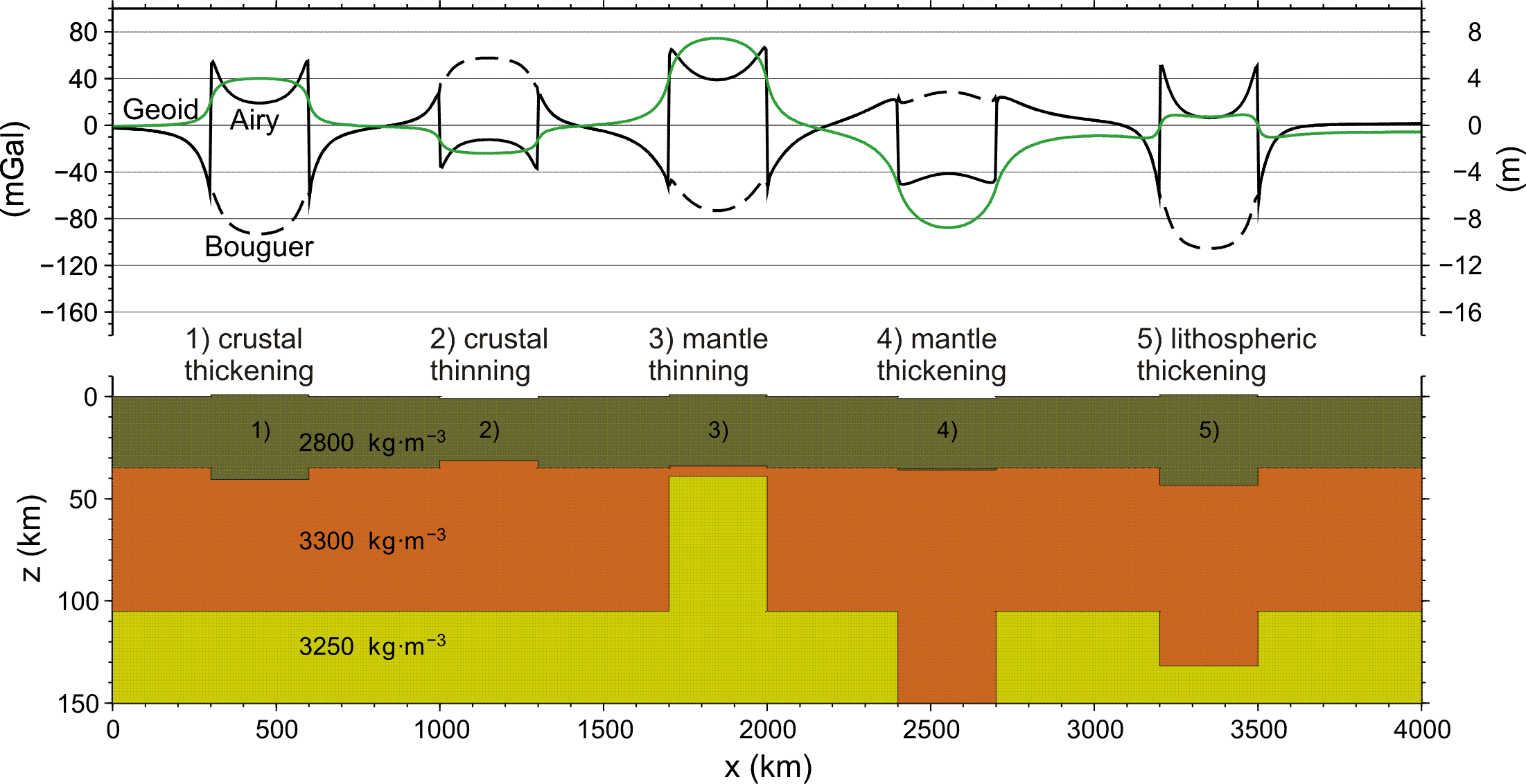
지오이드 표면 높이의 변화는 지구 내부의 이상적인 밀도 분포와 관련이 있다. 지오이드 측정은 행성의 내부 구조를 이해하는 데 도움이 된다. 합성 계산에 따르면 두꺼워진 지각(예: 조산대에서 대륙 충돌에 의해 생성됨)의 지오이드 신호는 양의 값을 가지며, 두꺼워짐이 전체 암석권에 영향을 미치는 경우 예상되는 것과 반대이다. 맨틀 대류 또한 시간에 따라 지오이드의 모양을 변화시킨다.[15]
지오이드 표면은 양의 중력 이상 또는 음의 섭동 퍼텐셜(질량 과잉)이 있는 곳에서는 기준 타원체보다 높고, 음의 중력 이상 또는 양의 섭동 퍼텐셜(질량 부족)이 있는 곳에서는 기준 타원체보다 낮다.[16]
이러한 관계는 중력 퍼텐셜이 음의 값을 가지며 물체로부터의 거리에 반비례하도록 정의된다는 것을 상기하면 이해할 수 있다. 따라서 질량 과잉은 중력 가속도를 강화하지만 중력 퍼텐셜은 감소시킨다. 결과적으로 지오이드를 정의하는 등퍼텐셜 표면은 질량 과잉으로부터 멀어지는 방향으로 이동한다. 마찬가지로 질량 부족은 중력을 약화시키지만 주어진 거리에서 지오포텐셜을 증가시켜 지오이드가 질량 부족으로 이동하게 한다.
배경 매질에 국지적인 포함물이 존재하면 중력 가속도 벡터가 각각 더 무거운 또는 더 가벼운 물체를 향하거나 멀어지는 방향으로 약간 회전하여 등퍼텐셜 표면에 돌출부 또는 오목부를 생성한다.[17]
8. 시간적 변화
최근 GOCE 및 GRACE와 같은 위성 임무를 통해 시간에 따라 변하는 지오이드 신호 연구가 가능해졌다. GOCE 위성 데이터를 기반으로 한 최초의 결과물은 2010년 6월 유럽우주국을 통해 온라인으로 공개되었다.[20][21] ESA는 전례 없는 정확도와 공간 해상도로 지구 중력을 측정하기 위한 임무로 2009년 3월 위성을 발사했다. 2011년 3월 31일, 독일 뮌헨 공과대학교에서 개최된 제4회 국제 GOCE 사용자 워크숍에서 새로운 지오이드 모델이 공개되었다.[22] GRACE 데이터로 계산된 시간에 따라 변하는 지오이드를 사용한 연구는 전 지구 수문 순환,[23] 빙상의 질량 균형,[24] 그리고 빙하기 이후 융기에 대한 정보를 제공했다.[25] 빙하기 이후 융기 측정을 통해 시간에 따라 변하는 GRACE 데이터를 사용하여 지구 맨틀의 점성을 추론할 수 있다.[26]
9. 구면조화 함수 표현
구면조화 함수는 지오이드의 형태를 근사하는 데 자주 사용된다. 현재 가장 정확한 구면조화 함수 계수 집합은 EGM2020(Earth Gravitational Model 2020)이다. EGM2020은 국립 지구공간 정보국이 주도하는 국제 공동 프로젝트에서 결정되었다.[27]
EGM2020 모델에서 지구 중력 퍼텐셜(\(V\))을 나타내는 비회전 부분의 퍼텐셜 함수에 대한 수학적 설명은 다음과 같다.[27]
\(V=\frac{GM}{r}\left(1+{\sum_{n=2}^{n_\text{max}}}\left(\frac{a}{r}\right)^n{\sum_{m=0}^n}
\overline{P}_{nm}(\sin\phi)\left[\overline{C}_{nm}\cos m\lambda+\overline{S}_{nm}\sin m\lambda\right]\right)\)
여기서 \(\phi\) 와 \(\lambda\)는 각각 지구 중심(구면) 위도와 경도이고, \(\overline{P}_{nm}\)는 차수 \(n\)와 위수 \(m\)의 완전 정규화된 연관 르장드르 다항식이며, \(\overline{C}_{nm}\)와 \(\overline{S}_{nm}\)는 측정된 데이터를 기반으로 하는 모델의 수치 계수이다.
위의 방정식은 지오이드 자체가 아니라 지구 중력 퍼텐셜 \(V\)를 지구 중심으로부터의 거리\(r\)의 위치 \(\phi,\;\lambda,\;r,\)에서 설명하며, 지오이드는 이 퍼텐셜의 등퍼텐셜면 중 하나이다.[27]
가장 일반적으로 사용되는 EGM96은 360차와 위수까지의 완전한 계수 집합(\(n_\text{max} = 360\))을 포함하고 있으며, 전 세계 지오이드의 세부 사항을 최대 55km(또는 해상도의 정의에 따라 110km)까지 설명한다.
EGM96 이후에 더 높은 해상도의 모델이 개발되었다. EGM96의 저자 중 많은 수가 새로운 위성 중력 데이터(예: 중력 복원 및 기후 실험)가 통합된 EGM2008을 발표했으며, 최대 2160차와 위수를 지원한다.
9. 1. GPS/GNSS와의 관계
GPS 시스템이나 GNSS는 타원체 고도를 제공하지만, 지도나 일반적인 사용에서는 평균 해수면 위의 높이(정고)를 사용한다.[5] 타원체고(''h'')와 정고(''H'') 사이의 편차(''N'')는 다음과 같이 계산할 수 있다.:
GPS 수신기는 세계측지계(WGS) 타원체 위의 지오이드 높이(예: EGM96 지오이드)를 이용하여 WGS 타원체 위의 높이를 EGM96 지오이드 위의 높이로 보정할 수 있다.
참조
[1]
웹사이트
WGS 84, N=M=180 Earth Gravitational Model
http://earth-info.ng[...]
National Geospatial-Intelligence Agency
2016-12-17
[2]
서적
Bestimmung des Breitenunterschiedes zwischen den Sternwarten von Göttingen und Altona durch Beobachtungen am Ramsdenschen Zenithsector
https://books.google[...]
Vandenhoeck und Ruprecht
2021-07-06
[3]
서적
Geodesy: The Concepts
Elsevier
[4]
웹사이트
Earth's Gravity Definition
http://www2.csr.utex[...]
Center for Space Research (University of Texas at Austin) / Texas Space Grant Consortium
2018-01-22
[5]
웹사이트
GPS Orthometric Height
http://www.edu-obser[...]
2016-06-15
[6]
서적
Encyclopedia of Geodesy
Springer International Publishing
[7]
서적
Encyclopedia of Solid Earth Geophysics
[8]
서적
Encyclopedia of Solid Earth Geophysics
[9]
웹사이트
UNB Precise Geoid Determination Package
http://www2.unb.ca/g[...]
2007-10-02
[10]
학술지
The Canadian geoid-Stokesian approach
[11]
학술지
Compilation of a precise regional geoid
http://gge.unb.ca/Pe[...]
[12]
보고서
Compilation of a Precise Regional Geoid
http://gge.unb.ca/Pe[...]
Department of Geodesy and Geomatics Engineering, University of New Brunswick
2016-12-22
[13]
서적
Relativistic celestial mechanics of the solar system
https://archive.org/[...]
Wiley-VCH
[14]
학술지
Spatial uncertainty of a geoid undulation model in Guayaquil, Ecuador
[15]
학술지
Geoid anomalies in a dynamic Earth
[16]
서적
The Solid Earth; An Introduction to Global Geophysics
Cambridge University Press
[17]
서적
Fundamentals of Geophysics
https://books.google[...]
Cambridge University Press
2022-05-02
[18]
웹사이트
The missing mass -- what is causing a geoid low in the Indian Ocean?
https://blogs.agu.or[...]
2022-05-02
[19]
학술지
North Atlantic geoid high, volcanism and glaciations
[20]
웹사이트
ESA makes first GOCE dataset available
http://www.esa.int/S[...]
European Space Agency
2016-12-22
[21]
웹사이트
GOCE giving new insights into Earth's gravity
http://www.esa.int/S[...]
European Space Agency
2016-12-22
[22]
웹사이트
Earth's gravity revealed in unprecedented detail
http://www.esa.int/e[...]
European Space Agency
2016-12-22
[23]
학술지
GRACE observations of changes in continental water storage
[24]
학술지
Interannual variations of the mass balance of the Antarctica and Greenland ice sheets from GRACE
[25]
학술지
Use of GRACE determined secular gravity rates for glacial isostatic adjustment studies in North-America
[26]
학술지
Inference of mantle viscosity from GRACE and relative sea level data
[27]
서적
IGeS Bulletin No. 8
International Geoid Service
2016-12-16
[28]
논문
Gravitational potential expansion to degree 2160
[29]
웹사이트
Earth Gravitational Model 2008 (EGM2008)
http://earth-info.ng[...]
National Geospatial-Intelligence Agency
2008-09-09
[30]
학술지
Earth Gravitational Model 2020
https://ui.adsabs.ha[...]
[31]
서적
萩原(1982)
[32]
웹사이트
日本での位置の基準となる測地系
https://www.gsi.go.j[...]
国土地理院
[33]
웹사이트
ジオイドとは
http://vldb.gsi.go.j[...]
国土地理院
[34]
웹사이트
ジオイド測量、ジオイドとは、図-2 楕円体・ジオイド・標高の関係
https://www.gsi.go.j[...]
[35]
웹사이트
基準点成果等閲覧サービス
https://sokuseikagis[...]
国土地理院
2014-03-13
[36]
웹사이트
ジオイドモデル、「日本のジオイド2011」(Ver. 2.1)
https://www.gsi.go.j[...]
国土地理院
[37]
논문
Geoid anomalies in a dynamic mantle
1984
[38]
서적
토목기사 과년도 시리즈 - 측량학
성안당
2015
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com