케플러의 행성운동법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사적 배경
- 2.1. 코페르니쿠스와의 비교
- 2.2. 케플러 법칙에 대한 비판과 수용
3. 케플러의 법칙
4. 수학적 설명
- 4.1. 뉴턴 역학과의 관계
5. 현대적 의의 및 활용
- 5.1. 한국 천문학에의 기여
참조

1. 개요

케플러의 행성 운동 법칙은 요하네스 케플러가 티코 브라헤의 관측 자료를 분석하여 1609년과 1619년에 발표한 세 가지 법칙으로, 행성의 운동을 설명한다. 제1법칙은 행성이 태양을 한 초점으로 하는 타원 궤도를 따라 움직인다는 것이고, 제2법칙은 행성과 태양을 잇는 선분이 같은 시간 동안 같은 면적을 쓸고 지나간다는 면적 속도 일정의 법칙이며, 제3법칙은 행성 공전 주기의 제곱이 궤도 장반경의 세제곱에 비례한다는 조화의 법칙이다. 이 법칙들은 지동설을 지지하고 천동설을 대체하는 데 기여했으며, 뉴턴의 만유인력 법칙의 토대가 되었다.

더 읽어볼만한 페이지

1609년 과학 - 신천문학
신천문학은 요하네스 케플러가 1609년에 출판한 천문학 서적으로, 티코 브라헤의 관측 자료를 바탕으로 행성이 태양을 중심으로 타원 궤도를 그린다는 케플러의 행성 운동 법칙 중 처음 두 가지를 제시하며 천문학 연구에 큰 영향을 미쳤다.
1619년 과학 - 세계의 조화
요하네스 케플러가 1619년에 발표한 "세계의 조화"는 천체의 운동, 음악, 기하학 간의 조화로운 관계를 탐구하며 행성 운동 제3법칙을 제시하고 다면체 연구를 포함하는 책이다.
요하네스 케플러 - 케플러 초신성
케플러 초신성은 1604년에 관측된 밝은 초신성으로, 여러 문명에서 기록되었으며, Ia형 초신성으로 추정되고 천문학 연구의 대상이 되었다.
요하네스 케플러 - 1134 케플러
1134 케플러는 태양을 약 4년 5개월 주기로 공전하는 S형 소행성으로, 행성 운동 법칙으로 유명한 천문학자 요하네스 케플러의 300주기 사망 기념으로 명명되었으며 지름은 약 3~8km로 추정된다.

케플러의 행성운동법칙
케플러 행성 운동 법칙
케플러 법칙
법칙 내용
제1 법칙 (타원 궤도의 법칙)	행성은 태양을 한 초점으로 하는 타원 궤도를 따라 공전한다.
제2 법칙 (면적 속도 일정의 법칙)	행성이 동일한 시간 간격 동안 휩쓸고 지나가는 면적은 항상 같다.
제3 법칙 (조화의 법칙)	행성 공전 주기의 제곱은 궤도 긴반지름의 세제곱에 비례한다.
설명
제1 법칙 (타원 궤도의 법칙)	궤도는 초점 F1과 F2를 가지는 타원이며, 행성 1은 F1을, 행성 2는 F1과 F3을 초점으로 한다.
제2 법칙 (면적 속도 일정의 법칙)	행성 1의 궤도에서 같은 시간 동안 휩쓸고 지나가는 면적 A1과 A2는 같다.
제3 법칙 (조화의 법칙)	행성 1의 공전 시간과 행성 2의 공전 시간의 비율은 (a1/a2)^(3/2)이다.
관련 항목
관련 주제	궤도 역학 천체 역학 항공우주공학
로마자 표기
케플러 법칙	Kepeulleo Beopchik

2. 역사적 배경

요하네스 케플러의 법칙은 16세기 니콜라우스 코페르니쿠스의 지동설에서 시작된 천문학 혁명의 연장선상에 있었다. 코페르니쿠스는 행성이 태양 주위를 원 궤도로 공전한다고 주장했지만, 관측 결과와 정확히 일치하지 않았다. 케플러는 스승인 티코 브라헤의 방대한 관측 자료를 분석하여 행성 운동에 대한 새로운 법칙을 발견했다.^[11] ^[12]^[13]^[14]^[15] 특히, 화성의 궤도를 정밀하게 분석하는 과정에서 행성 궤도가 원이 아닌 타원임을 알아냈다.

케플러는 1609년에 자신의 첫 번째와 두 번째 법칙을 발표했고,^[11] ^[12]^[13]^[14]^[15] 1619년에 세 번째 법칙을 발표했다.^[16]^[13] 케플러의 법칙은 당시 지배적이었던 아리스토텔레스의 우주관, 즉 천체는 완전한 원운동을 한다는 생각에 정면으로 도전하는 혁명적인 것이었다. 케플러의 법칙은 천동설에 대한 지동설의 우위를 결정적인 것으로 만드는데 기여했다.

에도 시대 일본의 천문학자 마다 고우리츠는 제3법칙과 유사한 법칙을 독자적으로 발견하여 『오성거지지기법(五星距地之奇法)』에 기록을 남기고 있다.^[41]

2. 1. 코페르니쿠스와의 비교

니콜라우스 코페르니쿠스는 행성이 주전원을 그리며 원 궤도로 등속 운동한다고 주장했지만, 요하네스 케플러는 행성이 타원 궤도로 운동하며 속도가 일정하지 않다고 밝혔다.^[1]^[2]^[15] 코페르니쿠스는 태양이 궤도의 중심에 있다고 보았지만, 케플러는 태양이 타원 궤도의 초점 중 하나에 위치한다고 보았다.^[3]^[4] 케플러는 행성의 면속도(역사적으로 각운동량 개념과 밀접하게 관련됨)가 일정하다는 법칙을 발견하여, 행성이 태양에 가까워질수록 속도가 빨라진다는 것을 설명했다.

이심률 때문에 지구 궤도에서 춘분부터 추분까지의 시간(약 186일)은 추분부터 춘분까지의 시간(약 179일)과 같지 않다.

케플러는 티코 브라헤의 천문 관측 자료를 분석하여 1609년에 행성 운동에 관한 그의 첫 번째와 두 번째 법칙을 발표했고,^[11] ^[12]^[13]^[14]^[15] 세 번째 법칙은 1619년에 발표되었다.^[16]^[13] 케플러는 코페르니쿠스 모델을 믿었고, 이는 원형 궤도를 요구했지만, 브라헤의 매우 정밀한 관측 결과를 화성의 궤도에 대한 원형 적합과 조화시킬 수 없었다. 화성은 수성을 제외하고 모든 행성 중에서 이심률이 가장 높았기 때문이다.^[17]

케플러의 법칙은 천동설에 대한 지동설의 우위를 결정적인 것으로 만들었다. 코페르니쿠스에 의해 지동설이 제창된 이후에도, 지동설에 기반한 행성 운동 모델은 종래의 천동설 모델과 비교하여 실용적으로 반드시 우수한 것은 아니었다. 그러나 케플러 법칙의 등장으로 지동설 모델은 천동설 모델보다 훨씬 정확하게 행성의 운동을 기술할 수 있게 되었다.

2. 2. 케플러 법칙에 대한 비판과 수용

케플러 법칙이 현재와 같이 공식화되기까지는 거의 2세기가 걸렸다. 볼테르의 1738년 저서 《뉴턴 철학의 요소들》(Eléments de la philosophie de Newton)은 "법칙"이라는 용어를 사용한 최초의 출판물이었다.^[5]^[6] 《천문학자 전기 백과사전》(Biographical Encyclopedia of Astronomers)의 케플러 항목(620쪽)에서는 이러한 발견에 대한 과학 법칙이라는 용어가 적어도 조제프 르 랑드 시대부터 사용되었음을 밝히고 있다.^[7] 로버트 스몰은 《케플러의 천문학적 발견에 대한 설명》(An account of the astronomical discoveries of Kepler, 1814)에서 세 번째 법칙을 추가하여 세 가지 법칙의 집합을 구성했다.^[8] 스몰은 또한 역사적 사실과는 달리 이것들이 귀납적 추론에 기반한 경험 법칙이라고 주장했다.^[6]^[9]

"케플러의 제2법칙"은 다소 잘못된 명칭이다. 케플러는 질적으로 관련된 두 가지 버전, 즉 "거리 법칙"과 "면적 법칙"을 가지고 있었다. "면적 법칙"이 세 가지 법칙 중 제2법칙이 되었지만, 케플러 자신은 그렇게 특별히 여기지 않았다.^[10]

3. 케플러의 법칙

케플러의 법칙은 다음과 같이 세 가지로 요약된다.

제1법칙 (타원 궤도의 법칙): 행성은 태양을 한 초점으로 하는 타원 궤도를 따라 운동한다.
제2법칙 (면적 속도 일정의 법칙): 행성과 태양을 연결하는 선분은 같은 시간 동안 같은 면적을 쓸고 지나간다.
케플러의 제2법칙
제3법칙 (조화의 법칙): 행성의 공전 주기의 제곱은 궤도의 긴반지름의 세제곱에 비례한다.

요하네스 케플러는 티코 브라헤의 관측 자료를 바탕으로 이 법칙들을 발견했다. 케플러의 법칙은 행성 운동을 정확하게 기술하며, 아이작 뉴턴의 만유인력의 법칙으로 설명할 수 있다.

제2법칙에서 면적속도는 수학적으로 다음과 같이 정의된다.

:

\dot{S} = {1 \over 2} r^2 \dot{\theta}

이는 행성 운동의 운동 상수를 의미하며, 행성의 공전 속도를 사용하여 다음과 같이 표현할 수도 있다.

:

\mathbf{r} \times \mathbf{v} = \textrm{const}

이 값은 행성의 각운동량에 비례하므로, 제2법칙은 만유인력의 법칙과 관계없이 각운동량 보존 법칙으로부터 유도할 수 있다.

제3법칙은 태양계에서 행성의 질량이 태양에 비해 매우 작으므로(

M>>m

), 다음과 같이 근사할 수 있다.

:

T^2 \simeq {4\pi^2 \over G M} a^3

따라서 태양을 중심으로 하는 태양계 안의 모든 행성에 대해서는

T^2 a^{-3}

의 값이 모두 같다. 케플러의 제3법칙은 비리얼 정리의 특수한 경우이다.

3. 1. 제1법칙: 타원 궤도의 법칙

요하네스 케플러가 발견한 케플러의 행성운동법칙 중 제1법칙은 '''궤도의 법칙'''이라고도 불린다.^[3] 행성의 공전 궤도는 타원 모양이며, 태양은 타원의 두 초점 중 하나에 위치한다.^[4]

니콜라우스 코페르니쿠스는 행성이 태양 주위를 공전한다고 주장했지만, 행성 궤도를 정확하게 정의하지 못했다. 요하네스 케플러는 코페르니쿠스의 모형을 개선하여 행성 궤도를 다음과 같이 정확하게 정의하였다.^[1]^[2]^[15]

행성 궤도는 주전원에 주전원을 더한 원이 아니라, 타원이다.
태양은 중심에 있지 않고 타원 궤도의 초점에 있다.
행성의 궤도에서 선속도나 각속도는 일정하지 않지만, 면속도(역사적으로 각운동량 개념과 밀접하게 관련됨)는 일정하다.

수학적으로 타원은 다음 공식으로 나타낼 수 있다.

:

r = \frac{p}{1 + \varepsilon\, \cos\theta},

여기서

p

는 반직선, ''ε''는 타원의 이심률, ''r''은 태양에서 행성까지의 거리, ''θ''는 태양에서 본 행성의 근일점으로부터의 현재 위치까지의 각도이다. 따라서 (''r'', ''θ'')는 극좌표이다.

타원의 경우 0 < ''ε'' < 1이다. ''ε'' = 0인 극한 경우, 궤도는 중심에 태양이 있는 원이다(즉, 이심률이 0인 경우).

''θ'' = 0°, 근일점에서 거리는 최소이다.

:

r_\min = \frac{p}{1 + \varepsilon}

''θ'' = 90° 및 ''θ'' = 270°에서 거리는

p

와 같다.

''θ'' = 180°, 원일점에서 거리는 최대이다(정의에 따라 원일점은 항상 근일점에 180°를 더한 값이다).

:

r_\max = \frac{p}{1 - \varepsilon}

장반축 ''a''는 ''r''_min과 ''r''_max의 산술 평균이다.

:

\begin{align}a &= \frac{r_\max + r_\min}{2} \\[3pt]a &= \frac{p}{1 - \varepsilon^2}\end{align}

단반축 ''b''는 ''r''_min과 ''r''_max의 기하 평균이다.

:

\begin{align}b &= \sqrt{r_\max r_\min} \\[3pt]b &= \frac{p}{\sqrt{1 - \varepsilon^2}}\end{align}

반직선 ''p''는 ''r''_min과 ''r''_max의 조화 평균이다.

:

\begin{align}p &= \left(\frac{r_\max^{-1} + r_\min^{-1}}{2}\right)^{-1} \\pa &= r_\max r_\min = b^2\,\end{align}

이심률 ''ε''는 ''r''_min과 ''r''_max의 변동 계수이다.

:

\varepsilon = \frac{r_\max - r_\min}{r_\max + r_\min}.

타원의 넓이는

:

A = \pi a b\,.

원인 특수한 경우는 ''ε'' = 0이며, ''r'' = ''p'' = ''r''_min = ''r''_max = ''a'' = ''b'' 및 ''A'' = ''πr''²를 만든다.

케플러는 티코 브라헤의 관측 기록을 바탕으로^[36] 태양에 대한 화성의 운동을 추정하여^[37] 다음과 같이 공식화했다.

;제1법칙 (타원 궤도의 법칙)

:행성은 태양을 한 초점으로 하는 타원 궤도 위를 움직인다.^[38]

:태양의 위치를 원점으로 하고, 태양과 행성의 거리 , 진근점각 를 매개변수로 하는 극좌표계에서 행성의 궤도는 다음 식으로 주어진다.

::

r=\frac{p}{1+\varepsilon\, \cos\theta}.

:여기서, 는 반직경(semi-latus rectum), 는 타원의 이심률이다. 단, 이며, 일 때는 태양 중심의 원궤도를 나타낸다.

제1법칙은 행성의 궤도가 원이 아니라 타원이며, 태양의 위치는 타원의 중심이 아니라 초점 중 하나라는 것을 설명한다(다른 한 초점에는 아무것도 없다). 또한 행성의 궤도가 태양을 포함하는 단일 평면상에 있다는 것을 암시적으로 의미한다. 후대의 뉴턴 역학에서는 중력이 작용하는 2체 문제의 해로서, 구속 운동이라면 타원 운동이 된다는 것이 증명된다.

당시 행성의 운동은 원이라고 믿어졌지만, 그것에 따르지 않는 화성의 데이터를 티코 브라헤가 어려워서 케플러에게 맡겼다는 이야기가 있다.

3. 2. 제2법칙: 면적 속도 일정의 법칙

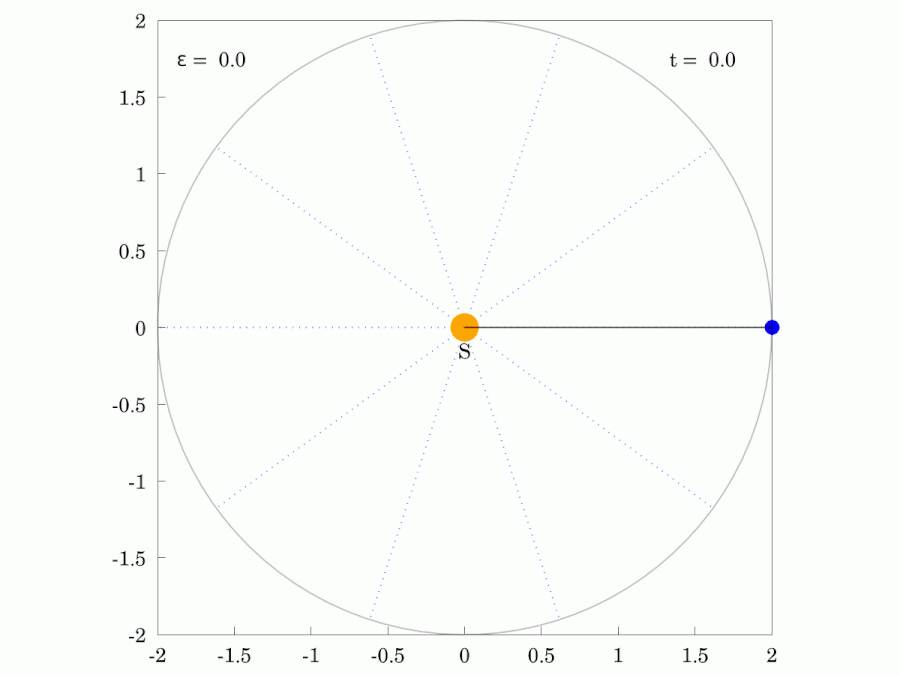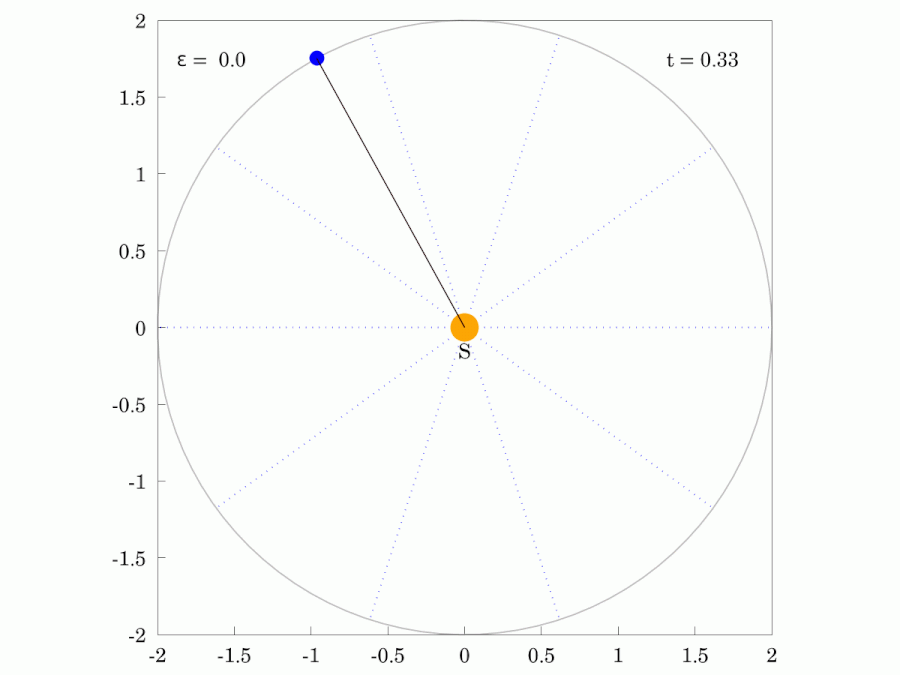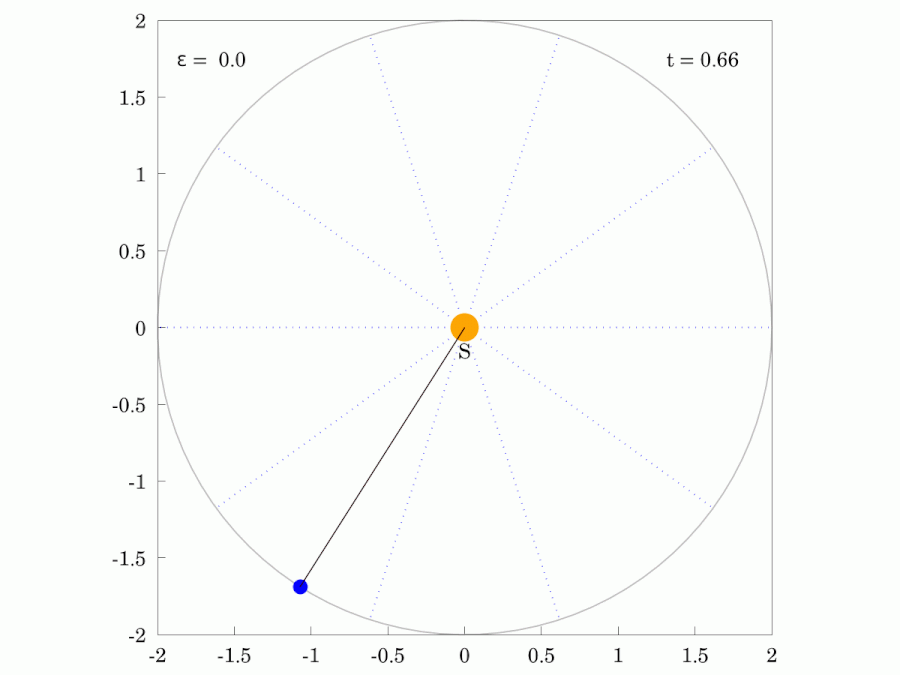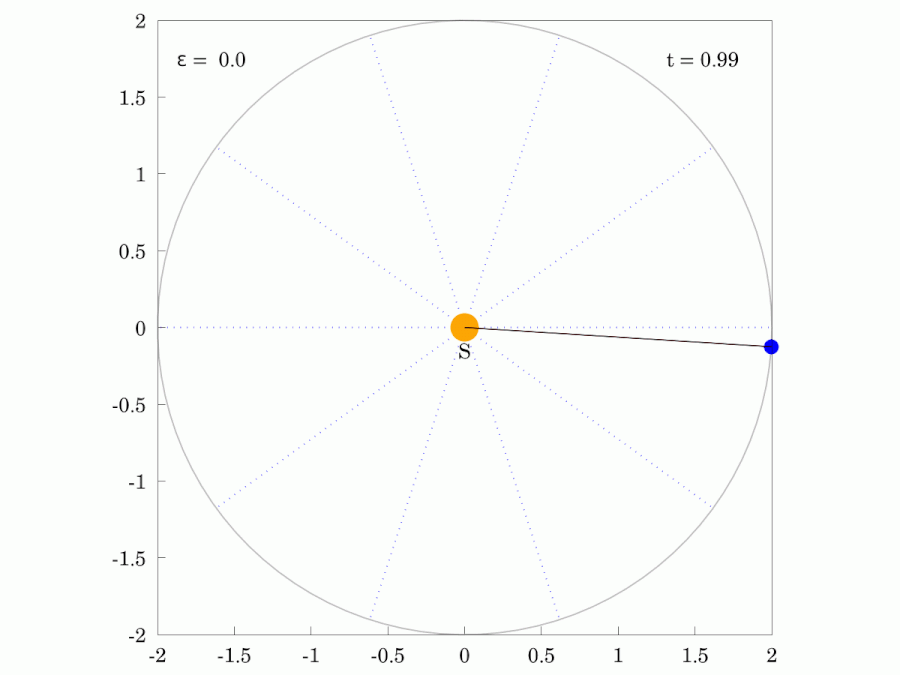
케플러의 제2법칙은 '''케플러 넓이 법칙'''(Kepler's law of areas^영어)이라고도 불린다. 이 법칙은 행성과 태양을 연결하는 가상의 선분이 같은 시간 동안 쓸고 지나가는 면적이 항상 같다는 것을 의미한다.^[1]^[2]^[15]

이는 행성이 태양에 가까워질수록 속도가 빨라지고, 멀어질수록 느려진다는 것을 뜻한다. 이 법칙은 각운동량 보존 법칙과 관련이 있다.^[24]

면적속도는 수학적으로 다음과 같이 정의된다.

:

\dot{S} = {1 \over 2} r^2 \dot{\theta}

케플러의 제2법칙은 행성 운동의 운동 상수임을 의미한다. 혹은, 행성의 공전 속도를 사용하여

:

\mathbf{r} \times \mathbf{v} = \textrm{const}

가 일정하다고 말하기도 한다. 위 값은 행성의 각운동량에 비례하므로, 이 법칙은 만유인력의 법칙과 관계없이 각운동량 보존 법칙으로부터 유도할 수 있다.

요하네스 케플러는 티코 브라헤의 천문 관측 자료를 분석하여 1609년에 이 법칙을 발표했다.^[11] ^[12]^[13]^[14]^[15]

제2법칙은 태양에 가까울수록 행성은 속도가 증가하고, 태양에서 멀어질수록 행성은 속도가 감소한다는 것을 의미한다. 이것은 행성이 궤도상을 이동할 때의 면적 속도가 일정하다는 것을 의미하며, “면적 속도 일정의 법칙”이라고도 불린다. 면적 속도는 행성의 위치 벡터와 속도 벡터의 외적과 같으며, 뉴턴 역학의 각운동량 보존 법칙에 해당한다.

극히 짧은 시간

dt

동안 행성은 밑변이

r

이고 높이가

r \, d\theta

인 작은 삼각형을 그리며, 면적은

dA = \frac{1}{2} \cdot r \cdot r \, d\theta

가 된다. 따라서 일정한 면적속도는

\frac{dA}{dt} = \frac{r^2}{2} \frac{d\theta}{dt}.

가 된다.

타원 궤도로 둘러싸인 면적은

\pi ab

이다. 따라서 주기

T

는 다음을 만족한다.

:

T \cdot \frac{r^2}{2} \frac{d\theta}{dt} = \pi ab

그리고 태양 주위를 도는 행성의 평균 운동

:

n = \frac{2\pi}{T}

는 다음을 만족한다.

:

r^2\,d\theta = abn\,dt.

따라서,

\frac{dA}{dt} = \frac{a b n}{2} = \frac{\pi a b}{T}.

케플러는 다음과 같은 가정을 통해 이 법칙에 도달했다.

# 행성은 태양으로부터 나오는 힘에 의해 태양 주위를 움직인다. (이는 물체가 운동을 유지하려면 밀어야 한다는 잘못된 아리스토텔레스적 물리학에 근거한다.)

# 태양으로부터 나오는 추진력은 태양으로부터의 거리에 반비례한다. (케플러는 중력이 3차원으로 퍼져나가는 것은 낭비라고 생각하여 이렇게 추론했다. 행성들은 평면에 존재하기 때문이다. 따라서 [정확한] 역제곱 법칙이 아닌 역제곱 법칙을 사용했다.)

# 케플러는 힘이 속도에 비례한다고 믿었기 때문에, 1번과 2번 문장에서 속도는 태양으로부터의 거리에 반비례한다는 결론을 얻었다. (이는 아리스토텔레스적 물리학의 잘못된 원리이다.)

# 속도가 시간에 반비례하기 때문에, 태양으로부터의 거리는 궤도의 작은 부분을 지나는 데 걸리는 시간에 비례한다. (이는 타원 궤도에서 대략적으로 참이다.)

# 휩쓸린 면적은 전체 시간에 비례한다. (이는 대략적으로 참이다.)

# 행성의 궤도는 원형이다 (케플러는 제1법칙보다 제2법칙을 먼저 발견했는데, 이는 이와 모순된다).

그럼에도 불구하고, 제2법칙의 결과는 정확하게 참이다. 이것은 각운동량 보존과 논리적으로 동등하며, 방사상 대칭적인 힘을 받는 모든 물체에 대해 참이다.^[26] 이를 통해 올바른 증명을 보일 수 있다. 두 벡터의 외적은 그 벡터들을 변으로 갖는 평행사변형의 면적을 주기 때문에, 짧은 시간 동안 휩쓸린 삼각형 면적 dA는 궤도의 어떤 짧은 부분 dx에 대해 r과 dx 벡터의 외적의 절반으로 주어진다.

dA = \frac{1}{2} (\vec{r} \times \vec{dx})= \frac{1}{2} (\vec{r} \times \vec{v} dt)

궤도의 작은 부분 dx와 그것을 지나는 데 걸리는 시간 dt에 대해.

따라서

\frac{dA}{dt} = \frac{1}{2} (\vec{r} \times \vec{v}).

\frac{dA}{dt} = \frac{1}{m} \frac{1}{2} (\vec{r} \times \vec{p}).

최종 표현식이 총 각운동량

(\vec{r} \times \vec{p})

에 비례하기 때문에, 케플러의 면적 속도 일정 법칙은 각운동량을 보존하는 모든 계에 대해 성립한다. 임의의 방사상 힘은 행성의 운동에 토크를 발생시키지 않으므로, 각운동량은 보존될 것이다.

이심률이 다른 행성의 궤도.
낮음	높음


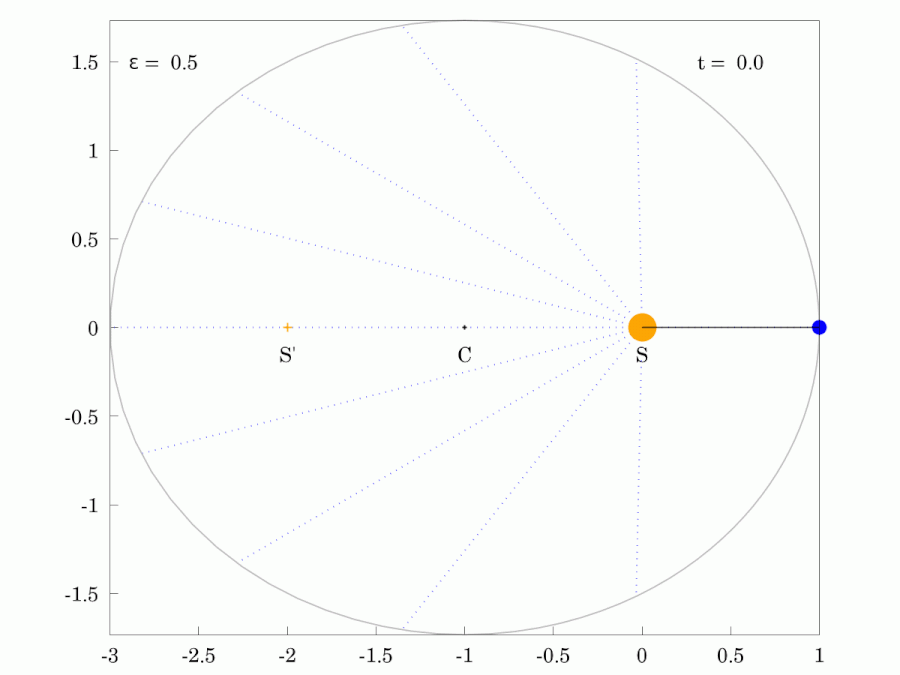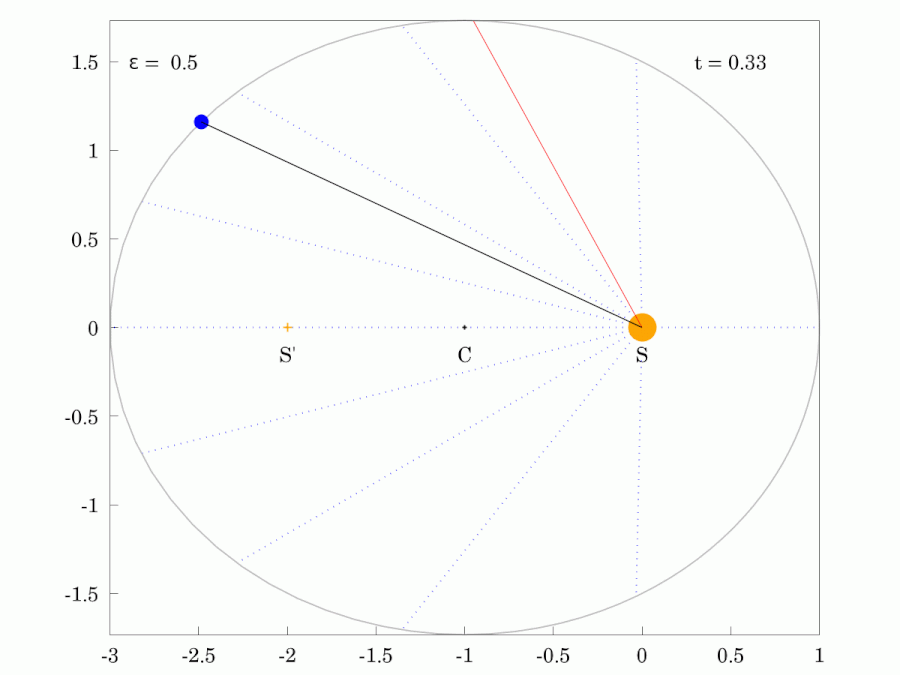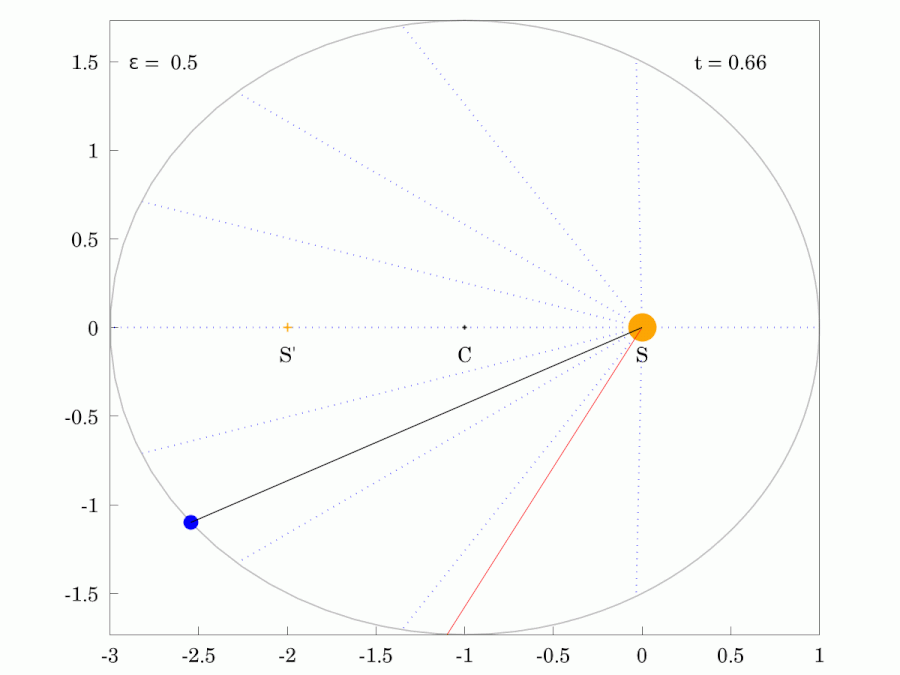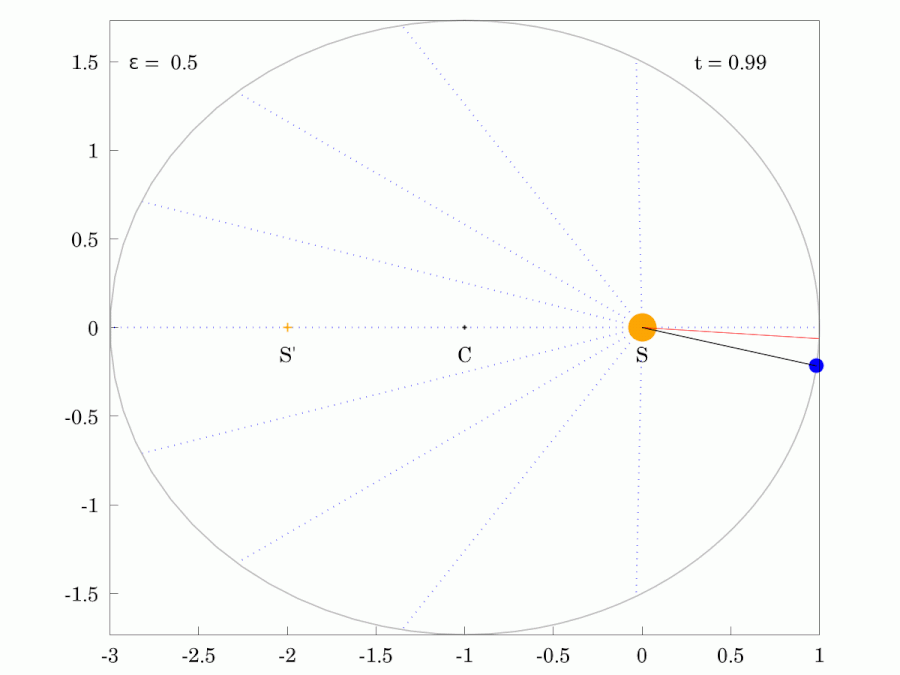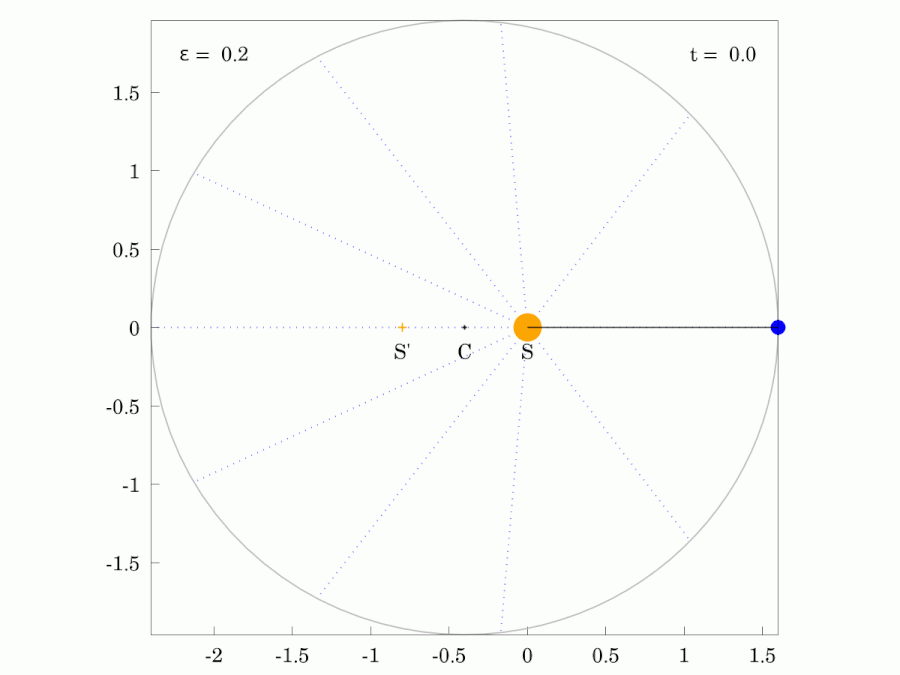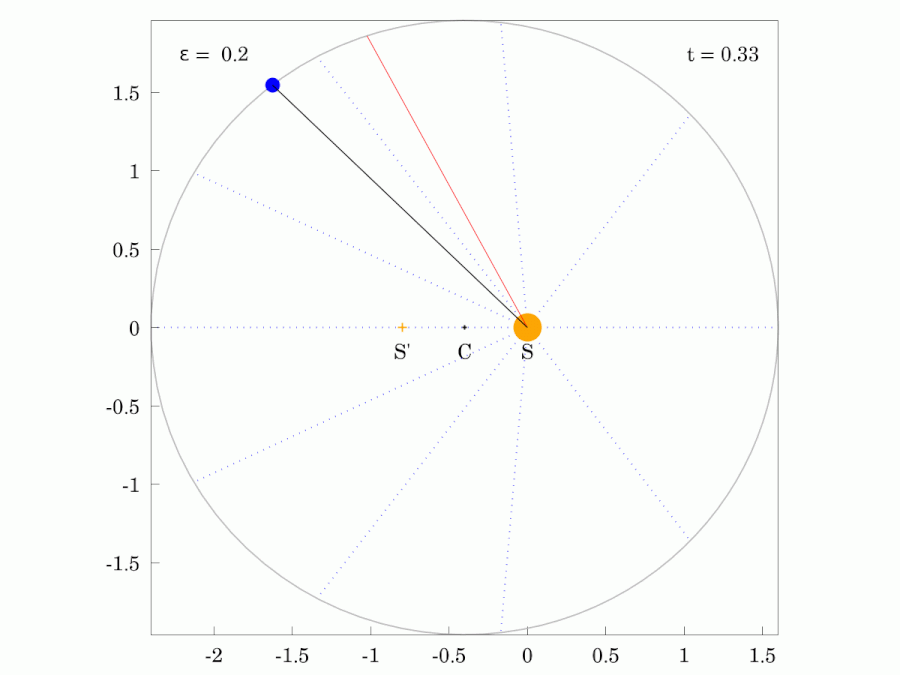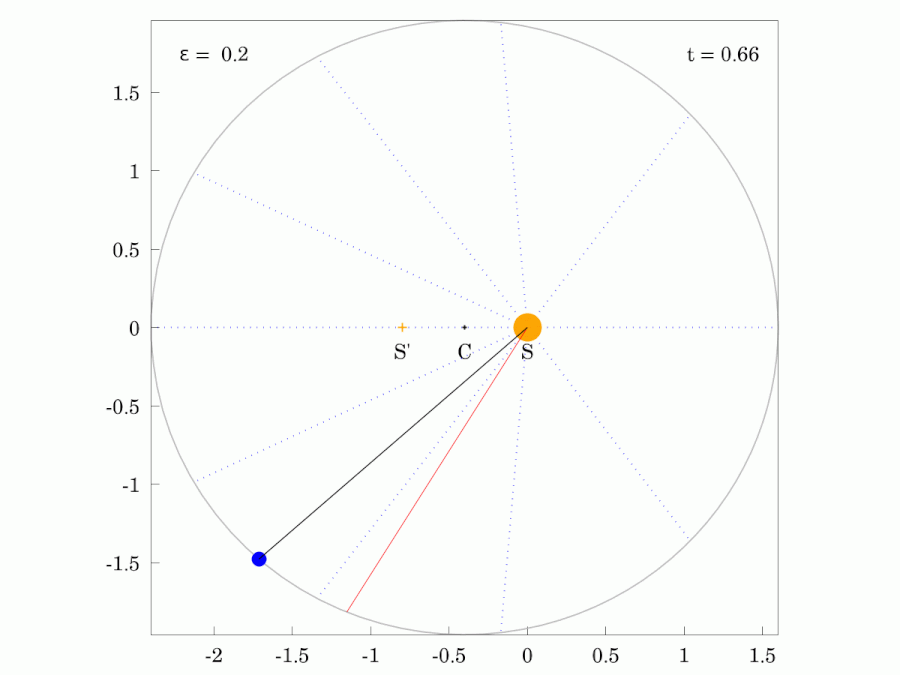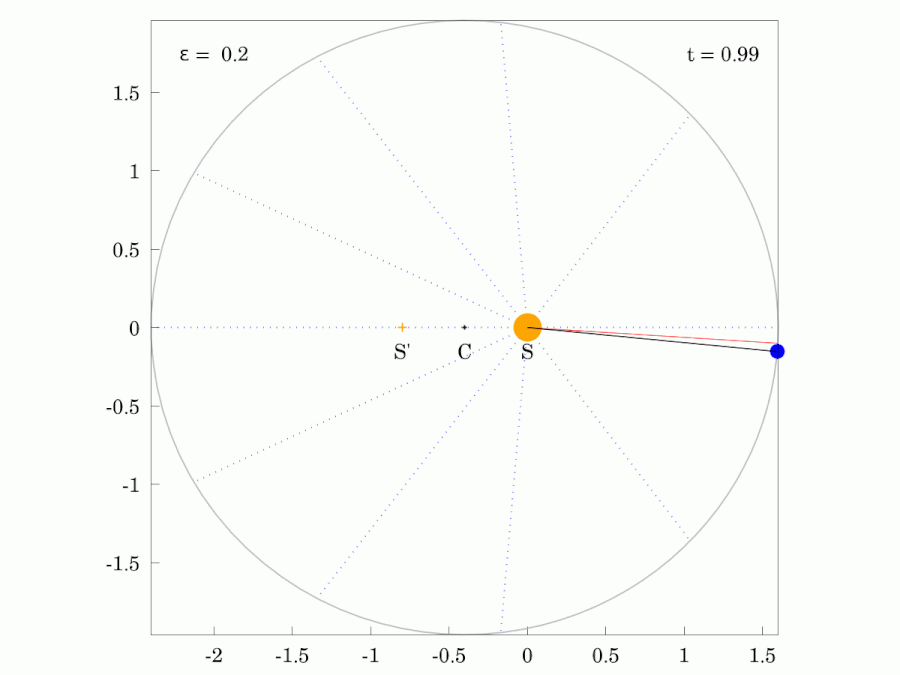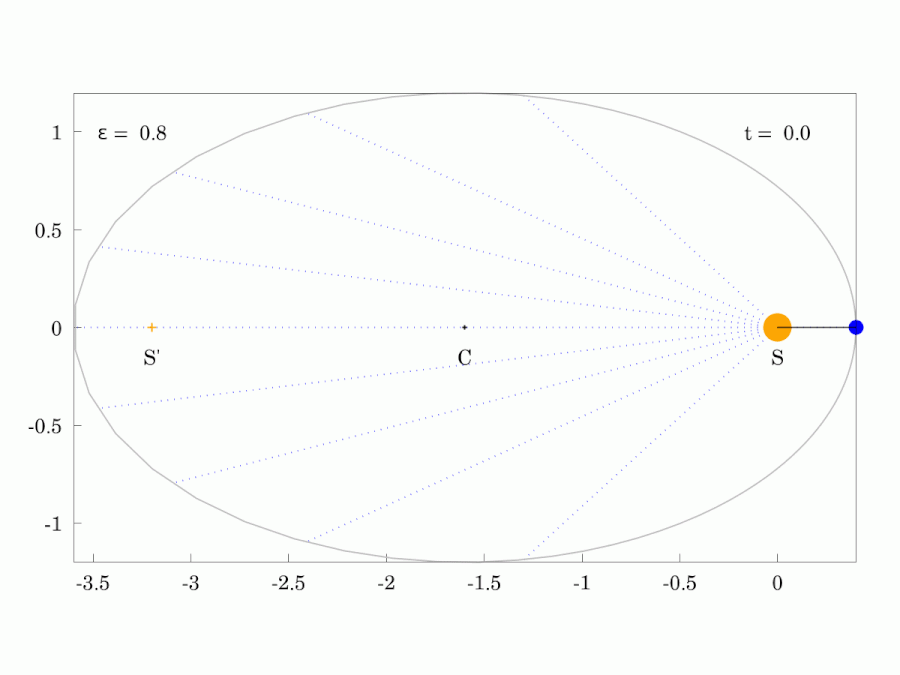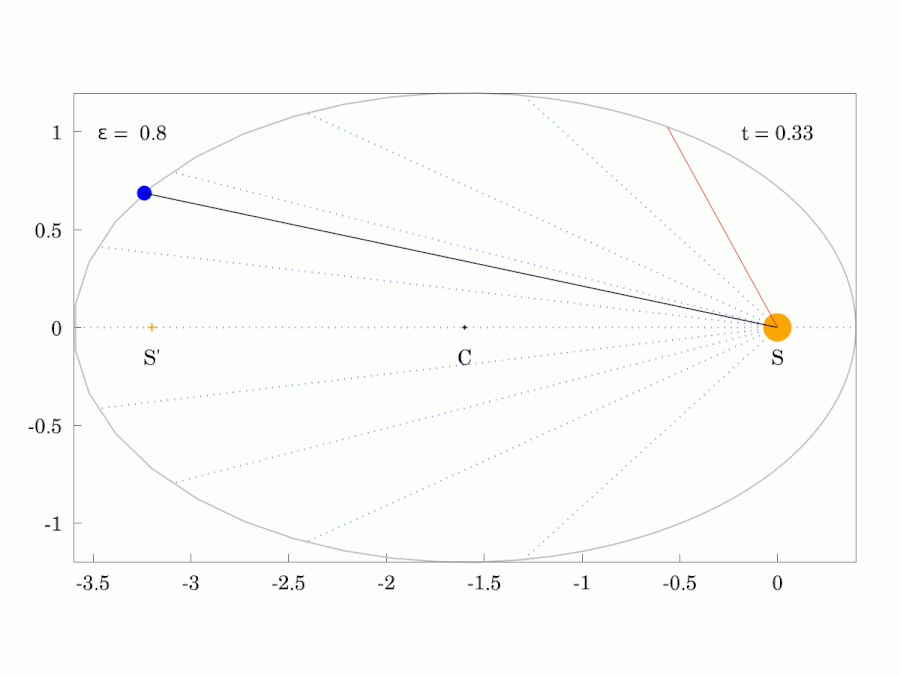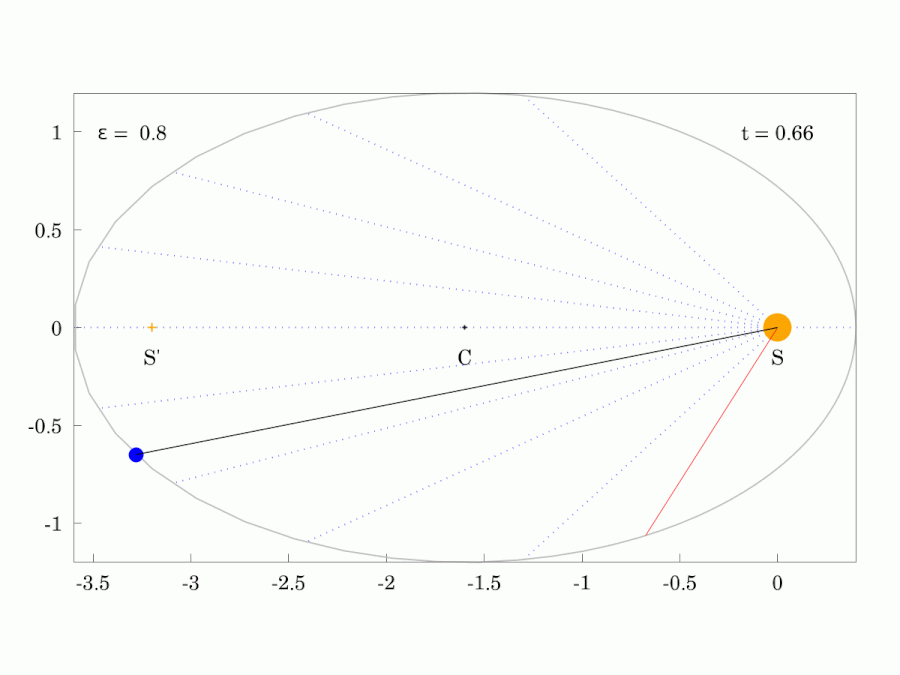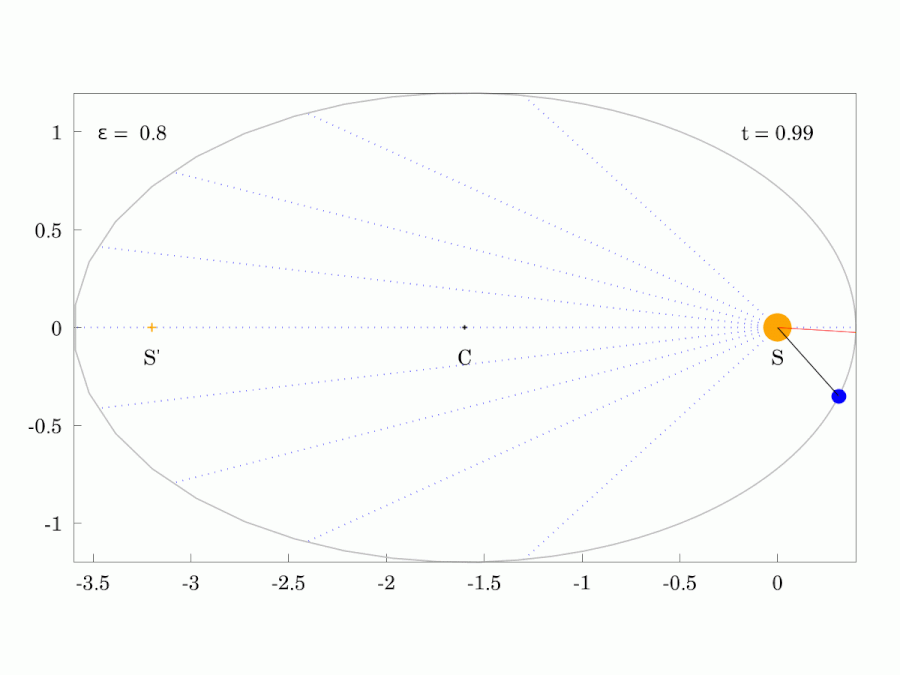붉은색 광선은 행성과 같은 궤도 주기 $T=1$ 로 일정한 각속도로 회전한다.

3. 3. 제3법칙: 조화의 법칙

케플러의 제3법칙은 '''주기의 법칙'''이라고도 불린다. 이 법칙은 행성의 공전 주기의 제곱이 궤도의 긴반지름의 세제곱에 비례한다는 것을 나타낸다. 수식으로 표현하면 다음과 같다.

:

T^2 \propto a^3

여기서,

:

T

는 공전 주기

:

a

는 공전 궤도의 긴반지름

을 의미한다. 태양계에서 행성은 태양에 비해 훨씬 가벼우므로 (

M>>m

), 다음과 같이 근사할 수 있다.

:

T^2 \simeq {4\pi^2 \over G M} a^3

따라서, 태양을 중심으로 하는 태양계 안의 모든 행성에 대해선

T^2 a^{-3}

의 값이 모두 같다.

이 법칙은 비리얼 정리의 특수한 경우이기도 하다.

케플러는 1619년^[3] 이 법칙을 발표했는데, 그는 이 법칙을 통해 "천구의 음악"을 결정하려고 했다.^[27] 그래서 이 법칙은 '조화 법칙'으로도 알려져 있다.^[28]

뉴턴의 만유인력 법칙(1687년 발표)을 사용하면, 원형 궤도의 경우 구심력을 만유인력과 같다고 설정하여 이 관계를 찾을 수 있다.

:

mr\omega^2 = G\frac{mM}{r^2}

각속도 ω를 궤도 주기

{T}

로 표현하고 정리하면 케플러의 제3법칙을 얻을 수 있다.

:

mr\left(\frac{2\pi}{T}\right)^2 = G\frac{mM}{r^2} \implies T^2 = \left(\frac{4\pi^2}{GM} \right)r^3 \implies T^2 \propto r^3

좀 더 자세한 유도는 원 대신 타원 궤도를 사용하고, 질량 중심을 고려하여 수행할 수 있다. 이 경우, 원형 반지름

r

은 타원형 상대 운동의 긴반지름

a

로 바뀌고, 큰 질량

M

은

M + m

으로 바뀐다. 그러나 행성의 질량은 태양보다 훨씬 작기 때문에, 이러한 수정은 종종 무시된다.

케플러가 법칙을 유도하는 데 사용한 데이터와 현대의 추정치는 아래 표와 같다.

케플러 (1618년)가 사용한 데이터^[30]^[31]
행성	태양까지의 평균 거리 (AU)	공전 주기 (일)	$\frac{R^3}{T^2}$ (10^-6 AU³/day²)
수성	0.389	87.77	7.64
금성	0.724	224.70	7.52
지구	1	365.25	7.50
화성	1.524	686.95	7.50
목성	5.20	4332.62	7.49
토성	9.510	10759.2	7.43

현대 데이터
행성	궤도 장반축 (AU)	공전 주기 (일)	$\frac{a^3}{T^2}$ (10^-6 AU³/day²)
수성	0.38710	87.9693	7.496
금성	0.72333	224.7008	7.496
지구	1	365.2564	7.496
화성	1.52366	686.9796	7.495
목성	5.20336	4332.8201	7.504
토성	9.53707	10775.599	7.498
천왕성	19.1913	30687.153	7.506
해왕성	30.0690	60190.03	7.504

4. 수학적 설명

케플러의 법칙은 극좌표계를 이용하여 수학적으로 표현할 수 있다. 행성의 궤도를 태양이 중심에 있는 극좌표계 $(r,\; \theta)$ 를 이용하면 케플러의 행성운동법칙을 간단하게 기술할 수 있다.

$\epsilon \equiv \sqrt{1+\left( {2EL^2 \over m\alpha}\right)}$ : 이심률
$\alpha \equiv GMm$
$L$ : 행성의 각운동량
$M$ : 초점에 위치한 별의 질량
$m$ : 행성의 질량
$E$ : 행성의 역학적 에너지
$G$ : 중력 상수

케플러는 자신의 처음 두 법칙을 이용하여 시간의 함수로서 행성의 위치를 계산했다. 그의 방법은 초월 방정식인 케플러 방정식의 해를 구하는 것을 포함한다. 근일점으로부터의 시간 ''t''의 함수로서 행성의 태양 중심 극좌표 (''r'',''θ'')를 계산하는 절차는 다음과 같다.

# 평균 운동

n = \frac{2\pi}{P}

을 계산한다. 여기서 ''P''는 주기이다.

# 평균 이상

M = nt

를 계산한다. 여기서 ''t''는 근일점 이후의 시간이다.

# 케플러 방정식

M = E - \varepsilon\sin E

를 풀어 이심 이상 ''E''를 계산한다. 여기서

\varepsilon

는 이심률이다.

# 다음 방정식을 풀어 진 이상 ''θ''를 계산한다.

(1 - \varepsilon) \tan^2 \frac{\theta}{2} = (1 + \varepsilon)\tan^2\frac{E}{2}

# 태양 중심 거리 ''r''을 계산한다.

r = a(1 - \varepsilon\cos E)

여기서

a

는 장반축이다.

케플러 문제는 타원 궤도와 다음 네 점을 가정한다.

''s'': 태양 (타원의 한 초점에 위치)
''z'': 근일점
''c'': 타원의 중심
''p'': 행성

그리고

$a = |cz|$ : 중심과 근일점 사이의 거리, 장반축

\varepsilon = \frac

{a}: 이심률

b = a\sqrt{1 - \varepsilon^2}

: 단반축

r = |sp|

: 태양과 행성 사이의 거리

\theta = \angle zsp

: 태양에서 보이는 행성의 방향, 진 이상

문제는 근일점 이후의 시간 ''t''로부터 행성의 극좌표 (''r'',''θ'')를 계산하는 것이다.

이 문제는 단계적으로 해결된다. 케플러는 장축을 지름으로 하는 원을 고려했고,

$x$ : 보조원에 대한 행성의 투영
$y$ : 부채꼴 영역 |''zcy''|와 |''zsx''|가 같은 점
$M = \angle zcy$ : 평균 이상

부채꼴 영역은

|zsp| = \frac{b}{a} \cdot |zsx|

의 관계가 있다.

원형 부채꼴 영역

|zcy| = \frac{a^2 M}2

근일점 이후 쓸린 면적,

|zsp| = \frac{b}{a} \cdot|zsx| = \frac{b}{a} \cdot |zcy| = \frac{b}{a} \cdot \frac{a^2 M}{2} = \frac{abM}{2}

은 케플러의 제2 법칙에 따라 근일점 이후의 시간에 비례한다. 따라서 평균 이상 ''M''은 근일점 이후의 시간 ''t''에 비례한다.

M = nt

여기서 ''n''은 평균 운동이다.

평균 이상 ''M''을 계산하면, 목표는 진 이상 ''θ''를 계산하는 것이다. 하지만 함수 ''θ'' = ''f''(''M'')는 초등함수가 아니다.^[35] 케플러의 해법은 이심 이상 ''E''를 중간 변수로 사용하여, 먼저 케플러 방정식을 풀어 ''M''의 함수로서 ''E''를 계산한 다음, 이심 이상 ''E''로부터 진 이상 ''θ''를 계산하는 것이다.

\begin{align}|zcy| &= |zsx| = |zcx| - |scx| \\|scx| &= \frac

{2} \\\frac{a^2 M}{2} &= \frac{a^2 E}2 - \frac{a\varepsilon \cdot a\sin E}{2}\end{align}

''a''²/2로 나누면 케플러 방정식이 된다.

M = E - \varepsilon\sin E.

이심 이상 ''E''를 계산한 후, 다음 단계는 진 이상 ''θ''를 계산하는 것이다.

그림에서 다음과 같은 관계를 알 수 있다.

|cd| = |cs| + |sd|

따라서

a\cos E = a \varepsilon + r\cos\theta.

a

로 나누고 케플러의 제1법칙

\frac{r}{a} = \frac{1 - \varepsilon^2}{1 + \varepsilon\cos\theta}

을 대입하면

\cos E = \varepsilon + \frac{1 - \varepsilon^2}{1 + \varepsilon\cos\theta} \cos\theta= \frac{\varepsilon (1 + \varepsilon\cos\theta) + \left(1 - \varepsilon^2\right)\cos\theta}{1 + \varepsilon\cos\theta}= \frac{\varepsilon + \cos\theta}{1 + \varepsilon\cos\theta}.

이 결과는 이심 근점 이각 ''E''와 진 근점 이각 θ 사이의 유용한 관계를 보여준다.

삼각 항등식을 이용하여 계산상 더 편리한 형태를 얻을 수 있다.

\tan^2\frac{x}{2} = \frac{1 - \cos x}{1 + \cos x}.

다음을 얻는다.

\begin{align}\tan^2\frac{E}{2}&= \frac{1 - \cos E}{1 + \cos E}= \frac{1 - \frac{\varepsilon + \cos\theta}{1 + \varepsilon\cos\theta}}{1 + \frac{\varepsilon + \cos \theta}{1 + \varepsilon\cos\theta}} \\[8pt]&= \frac{(1 + \varepsilon\cos\theta) - (\varepsilon + \cos\theta)}{(1 + \varepsilon\cos\theta) + (\varepsilon + \cos\theta)}= \frac{1 - \varepsilon}{1 + \varepsilon} \cdot \frac{1 - \cos\theta}{1 + \cos\theta}= \frac{1 - \varepsilon}{1 + \varepsilon} \tan^2\frac{\theta}{2}.\end{align}

1 + ''ε''을 곱하면 다음 결과를 얻는다.

(1 - \varepsilon)\tan^2\frac{\theta}{2} = (1 + \varepsilon)\tan^2\frac{E}{2}

이는 궤도에서 시간과 위치 간의 관계를 연결하는 세 번째 단계이다.

네 번째 단계는 케플러의 제1법칙을 이용하여 진 이상 θ로부터 태양 중심 거리 r을 계산하는 것이다.

r(1 + \varepsilon\cos\theta) = a\left(1 - \varepsilon^2\right)

θ와 E 사이의 위 관계식을 사용하면 거리 r에 대한 최종 방정식은 다음과 같다.

r = a(1 - \varepsilon\cos E).

케플러는 티코 브라헤의 관측 기록을 바탕으로^[36] 태양에 대한 화성의 운동을 추정하여^[37] 다음과 같이 공식화했다.

제1법칙 (타원 궤도의 법칙): 행성은 태양을 한 초점으로 하는 타원 궤도 위를 움직인다.^[38]

제2법칙과 제3법칙은 "뉴턴 역학과의 관계"에서 이미 상세히 다루고 있으므로, 여기서는 간략하게 언급만 한다.

제2법칙 (면적 속도 일정의 법칙): 행성과 태양을 잇는 선분이 단위 시간에 쓸고 지나가는 면적(면적 속도)은 일정하다.
제3법칙 (조화의 법칙): 행성의 공전 주기의 제곱은 궤도 장반경의 세제곱에 비례한다.

먼저 제1법칙과 제2법칙이 발견되어 1609년에 발표되었고,^[39] 나중에 제3법칙이 발견되어 1619년에 발표되었다.^[40]

4. 1. 뉴턴 역학과의 관계

아이작 뉴턴은 자신의 저서 ''자연철학의 수학적 원리''에서 케플러의 법칙을 운동 법칙과 만유인력 법칙으로 설명했다.^[32]^[33] 케플러의 법칙은 뉴턴의 만유인력 법칙의 특수한 경우로 설명될 수 있다. 뉴턴은 행성에 작용하는 힘을 질량과 가속도의 곱으로 정의하고, 모든 천체가 서로를 끌어당긴다는 가정을 통해 케플러의 법칙을 유도했다.

뉴턴의 이론에 따르면, 행성에 작용하는 중력은 다음과 같이 표현된다.

:

\mathbf{F} = m_\text{planet} \mathbf{\ddot{r}} = - m_\text{planet} \alpha r^{-2} \hat{\mathbf{r}}

여기서

m_\text{planet}

는 행성의 질량,

\alpha

는 태양계의 모든 행성에 대해 동일한 값 (

\alpha = G m_\text{Sun}

,

G

는 중력 상수)을 가진다. 즉, 행성에 작용하는 힘은 행성의 질량에 정비례하고 태양으로부터의 거리의 제곱에 반비례한다.

일반적으로 태양계 천체 i의 가속도는 다음과 같이 표현된다.

:

\mathbf{\ddot{r}}_i = G\sum_{j \ne i} m_j r_{ij}^{-2} \hat{\mathbf{r}}_{ij}

여기서

m_j

는 천체 j의 질량,

r_{ij}

는 천체 i와 천체 j 사이의 거리,

\hat{\mathbf{r}}_{ij}

는 천체 i에서 천체 j를 향하는 단위 벡터이다.

태양과 지구, 달과 지구와 같이 두 천체만 고려하는 경우, 위 식은 케플러 운동의 가속도와 같아진다. 즉, 이 근사에서 지구와 달은 케플러 법칙에 따라 운동한다.

세 천체의 경우, 가속도는 삼체 문제로 인해 복잡해지지만, 케플러 근사는 섭동 계산의 기초가 된다.

뉴턴 역학에서 중력이 작용하는 2체 문제를 풀면, 궤도는 타원이 된다. 케플러의 제2법칙은 각운동량 보존 법칙으로 설명되고, 제3법칙 또한 뉴턴 역학에서 유도 가능하다.

케플러의 법칙은 태양과 행성 사이뿐만 아니라, 행성과 위성 사이에도 성립한다. 또한, 제2, 제3법칙은 두 질점의 질량이 비슷하더라도 성립하며, 이를 통해 쌍성계, 이중 행성 등의 질량 합을 구할 수 있다. 궤도 장반축을 , 공전 주기를 , 주성의 질량을 , 동반성의 질량을 , 만유인력 상수를 라고 하면, 이들의 관계는 다음과 같다.

:

\frac{a^3}{P^2}=G\frac{M+m}{4\pi^2}.

5. 현대적 의의 및 활용

케플러의 법칙은 오늘날에도 천문학에서 널리 사용되며, 행성, 위성, 인공위성 등의 궤도를 계산하는 데 필수적이다.^[1] 우주 탐사선의 궤도를 설계하고 예측하는 데에도 케플러의 법칙이 활용된다.^[1] 케플러의 법칙은 천문학뿐만 아니라 물리학, 수학 등 다양한 분야에도 큰 영향을 미쳤다.^[1]

조선의 과학자 이순지는 케플러 법칙 이전에 이미 면적 속도 일정의 법칙과 유사한 개념을 알고 있었고, 홍대용은 의산문답에서 지동설을 주장하는 등 조선 시대에도 케플러의 법칙과 유사한 과학적 발견들이 있었다.

5. 1. 한국 천문학에의 기여

조선 시대의 천문학자 이순지는 케플러의 법칙이 도입되기 이전에 이미 면적 속도 일정의 법칙과 유사한 개념을 인지하고 있었다. 그는 자신의 저서에서 "행성이 태양에 가까울수록 움직임이 빠르다"고 기술하였다. 조선 후기 실학자 홍대용은 그의 저서 "의산문답"에서 지구가 둥글고 자전하며, 태양 주위를 공전한다는 지동설을 주장했다. 이는 케플러의 법칙과 맥락을 같이 하는 선구적인 주장이었다. 현대 한국 천문학은 케플러의 법칙을 바탕으로 우주 탐사, 인공위성 개발 등 다양한 분야에서 활약하고 있다.

참조

_[1] 웹사이트 Kepler's Laws http://hyperphysics.[...] 2022-12-13
_[2] 웹사이트 Orbits and Kepler's Laws https://solarsystem.[...] 2022-12-13
_[3] 웹사이트 Planetary Motion: The History of an Idea That Launched the Scientific Revolution https://earthobserva[...] 2022-12-13
_[4] 웹사이트 Nicolaus Copernicus https://www.history.[...] 2022-12-13
_[5] 서적 Eléments de la philosophie de Newton https://books.google[...] 1738
_[6] 간행물 Kepler's Laws, So-Called https://had.aas.org/[...] 2016-12-27
_[7] 서적 Astronomie https://books.google[...] 1764
_[8] 서적 An account of the astronomical discoveries of Kepler https://archive.org/[...] 1804
_[9] 서적 An account of the astronomical discoveries of Kepler https://archive.org/[...] 1804
_[10] 서적 Kepler's Physical Astronomy https://books.google[...] Princeton University Press 1994
_[11] 서적 Astronomia nova Aitiologitis, seu Physica Coelestis tradita Commentariis de Motibus stellae Martis ex observationibus G.V. Tychnonis 1609
_[12] 서적 Astronomia nova https://archive.org/[...] 1609
_[13] 서적 Physics, the Human Adventure: From Copernicus to Einstein and Beyond https://books.google[...] Rutgers University Press 2001
_[14] 서적 Astronomia nova https://archive.org/[...] 1609
_[15] 간행물 The great Martian catastrophe and how Kepler fixed it https://pubs.aip.org[...] 2011-00-00
_[16] 서적 Harmonices Mundi https://archive.org/[...] American Philosophical Society 1619
_[17] 웹사이트 Data Table for Planets and Dwarf Planets https://www.windows2[...] 2008-10-09
_[18] 서적 Epitome Astronomiae Copernicanae https://books.google[...] 1622
_[19] 서적 Almagestum novum https://books.google[...] 1651
_[20] 서적 Nicolai Mercatoris Hypothesis astronomica nova, et consensus eius cum observationibus Leybourn 1664
_[21] 간행물 Some considerations of Mr. Nic. Mercator, concerning the geometrick and direct method of signior Cassini for finding the apogees, excentricities, and anomalies of the planets; ... https://royalsociety[...] 1670-03-25
_[22] 서적 Encyclopedia of the Scientific Revolution: From Copernicus to Newton https://books.google[...] Routledge 2000
_[23] 서적 The Scientific Revolution in National Context https://archive.org/[...] Cambridge University Press 1992
_[24] 서적 Variations on a Theme by Kepler https://books.google[...] American Mathematical Soc. 2006
_[25] 웹사이트 Kepler's Second Law http://demonstration[...] 2009-12-27
_[26] 서적 Brush and Holton - Physics: the human adventure Princeton University Press 2001
_[27] 서적 The Metaphysical Foundations of Modern Physical Science
_[28] 서적 Physics, the Human Adventure https://books.google[...] Rutgers University Press 2001
_[29] 간행물 Original form of Kepler's Third Law and its misapplication in Propositions XXXII-XXXVII in Newton's Principia (Book I) 2019-00-00
_[30] 서적 Kepler https://archive.org/[...] Dover 1993
_[31] 서적 Kepler https://archive.org/[...] Dover 1993
_[32] 서적 Principia
_[33] 서적 Principia
_[34] 웹사이트 Memorandum № 1: Keplerian Orbit Elements → Cartesian State Vectors https://downloads.re[...] 2018-05-04
_[35] 웹사이트 Equation of Time – Problem in Astronomy http://info.ifpan.ed[...] Acta Physica Polonica A 1995-00-00
_[36] 서적 物理学通論 I 学術図書出版 2004
_[37] 서적 パリティ物理学コース力学丸善 2002
_[38] 서적 数学と理科の法則・定理集アントレックス
_[39] 서적 新天文学 (Astronomia Nova) 工作舎 2013
_[40] 서적 宇宙の調和 (Harmonice Mundi) 工作舎 2009
_[41] 서적 月のえくぼ（クレーター）を見た男麻田剛立くもん出版 2008
_[42] 서적 고등학교 고급물리 지학사 2006

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com