팀소트
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
팀소트는 대부분의 실제 데이터에 존재하는 정렬된 요소를 활용하여 효율적으로 정렬하는 알고리즘이다. 런(runs)이라고 불리는 정렬된 요소들을 스택에 쌓고, 특정 조건을 만족하면 병합하는 방식으로 작동하며, 입력 크기에 따라 최소 런 크기를 결정한다. 팀소트는 2의 거듭제곱과 유사한 크기의 런을 병합할 때 효율적이므로, minrun을 선택하여 이러한 조건을 만족시키도록 설계되었다. 병합 시에는 공간 오버헤드를 줄이기 위해 이진 검색을 활용하며, 갤로핑 모드를 통해 정렬 속도를 향상시키기도 한다. 팀소트는 최악의 경우 O(n log n)의 시간 복잡도를 가지며, 이미 정렬된 데이터에 대해서는 선형 시간 내에 실행되는 적응형 정렬 알고리즘이다. 하지만, 특정 입력에 대해 스택 크기 관련 버그가 발견되어 수정되었으며, 형식 검증을 통해 안정성을 강화했다.
더 읽어볼만한 페이지
- 안정 정렬 - 합병 정렬
합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다. - 안정 정렬 - 삽입 정렬
삽입 정렬은 미정렬 부분의 원소를 정렬된 부분의 올바른 위치에 삽입하여 정렬을 완성하는 간단하고 효율적인 알고리즘이지만, 데이터 세트가 클수록 성능이 저하되어 이를 개선하기 위한 변형 알고리즘이 존재한다. - 비교 정렬 - 합병 정렬
합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다. - 비교 정렬 - 퀵 정렬
퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다. - 정렬 알고리즘 - 합병 정렬
합병 정렬은 분할 정복 알고리즘을 사용하여 리스트를 재귀적으로 분할하고 정렬된 부분 리스트를 병합하는 비교 기반 정렬 알고리즘으로, O(n log n)의 시간 복잡도를 가지며 안정 정렬에 속하고 연결 리스트 정렬 및 외부 정렬에 유용하다. - 정렬 알고리즘 - 퀵 정렬
퀵 정렬은 토니 호어가 개발한 분할 정복 방식의 효율적인 정렬 알고리즘으로, 피벗을 기준으로 리스트를 분할하여 정렬하는 과정을 재귀적으로 반복하며 다양한 최적화 기법과 변형이 존재한다.
| 팀소트 | |
|---|---|
| 개요 | |
| 종류 | 정렬 알고리즘 |
| 자료 구조 | 배열 |
| 시간 복잡도 | 최선: O(n) 평균: O(n log n) 최악: O(n log n) |
| 공간 복잡도 | O(n) |
| 안정 정렬 여부 | 예 |
| 특징 | |
| 기반 알고리즘 | 삽입 정렬 합병 정렬 |
2. 작동 원리
팀소트는 대부분의 실제 데이터에 이미 존재하는 연속적인 정렬된 요소인 "런(runs)"을 활용한다. 이 런은 "자연 런"이라고도 불리며, 팀소트는 이를 통해 효율적인 정렬을 수행한다.
알고리즘은 입력 데이터를 반복하면서 요소를 런으로 수집하고, 동시에 해당 런을 스택에 넣는다. 스택 상단의 런이 병합 조건을 만족하면 병합을 수행한다. 모든 데이터를 탐색한 후에는 모든 런을 한 번에 두 개씩 병합하여 하나의 정렬된 런을 생성한다.
정렬된 런을 병합하는 방식은 고정 크기의 하위 목록을 병합하는 전통적인 병합 정렬 방식보다 전체 목록을 정렬하는 데 필요한 총 비교 횟수를 줄이는 장점이 있다.
각 런은 입력 크기를 기반으로 하는 최소 크기를 가지며, 알고리즘 시작 시 정의된다. 만약 런이 이 최소 런 크기보다 작으면, 삽입 정렬을 사용하여 최소 런 크기에 도달할 때까지 런에 더 많은 요소를 추가한다.
2. 1. 최소 런(Minrun)
팀소트는 대부분의 실제 데이터에 이미 존재하는 연속적인 정렬된 요소인 "런(runs)"을 활용한다. 각 런은 최소 크기(minrun)를 가지며, 이는 입력 데이터의 크기에 기반하여 결정된다. 런의 크기가 minrun보다 작으면 삽입 정렬을 사용하여 런의 크기를 minrun 이상으로 만든다.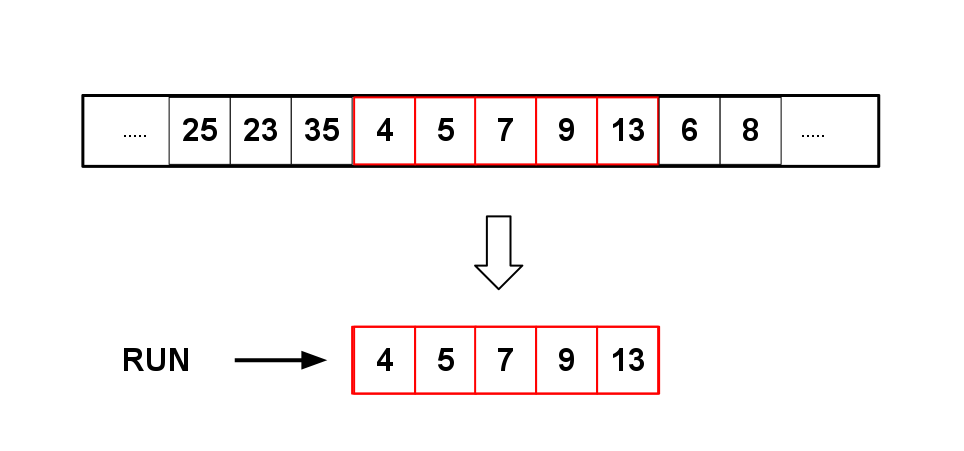
minrun은 32에서 64 사이의 값으로 선택되며, 데이터 크기를 minrun으로 나눈 값이 2의 거듭제곱에 가깝거나 같도록 한다. minrun을 정하는 일반적인 방법은 데이터 크기의 가장 중요한 6비트를 취하고, 나머지 비트 중 하나라도 설정되어 있으면 1을 더한 값을 사용하는 것이다.[13] 이 알고리즘은 64보다 작은 배열을 포함한 모든 배열에 적용되며, 크기가 63 이하인 배열의 경우 minrun을 배열 크기와 같게 설정하여 팀소트는 삽입 정렬로 축소된다.[13]
2. 2. 병합 조건
팀소트는 안정 정렬을 유지하고 균형 잡힌 병합을 수행하기 위해 스택 상단의 세 런 ''X'', ''Y'', ''Z''의 크기가 다음 조건을 만족시키도록 한다.
이 조건을 만족하지 않으면, ''Y''는 ''X'' 또는 ''Z'' 중 더 작은 런과 병합된다.[14] 이러한 불변성은 균형을 위해 병합을 지연시키는 것, 캐시 메모리에서 런의 새로운 발생을 활용하는 것, 그리고 병합 결정을 상대적으로 단순하게 만드는 것 사이에서 타협점을 유지하면서 병합을 대략적으로 균형 있게 유지한다.
2. 3. 병합 공간 오버헤드
팀소트는 병합 정렬의 공간 오버헤드를 줄이기 위해 최적화된 방법을 사용한다. 두 런(run)을 병합할 때, 더 작은 런을 임시 메모리에 복사하고, 이진 탐색을 사용하여 병합될 위치를 찾는다. 이를 통해 불필요한 요소 이동을 줄이고, 추가적인 메모리 사용량을 최소화한다.[13][14]
예를 들어, [1, 2, 3, 6, 10]과 [4, 5, 7, 9, 12, 14, 17] 두 런을 병합하는 경우를 생각해 보자. 두 번째 런의 첫 번째 요소(4)는 첫 번째 런의 네 번째 위치에, 첫 번째 런의 마지막 요소(10)는 두 번째 런의 다섯 번째 위치에 삽입되어야 한다. 따라서 [1, 2, 3]과 [12, 14, 17]은 이미 최종 위치에 있으므로, [6, 10]과 [4, 5, 7, 9]만 병합하면 된다. 이 경우 크기 2의 임시 버퍼만 할당하면 된다.
이처럼 팀소트는 더 작은 런을 임시 메모리로 복사하고, 이진 탐색으로 삽입 위치를 찾아 병합함으로써, 제자리 병합 정렬의 높은 시간 오버헤드를 피하면서도 공간 오버헤드를 줄일 수 있다.
2. 4. 병합 방향
병합은 전통적인 병합 정렬에서처럼 왼쪽에서 오른쪽으로 또는 오른쪽에서 왼쪽으로 양방향으로 수행할 수 있다. 팀소트는 대부분의 실제 데이터에 처음부터 존재하는, 연속된 요소의 ''자연스러운 순서''를 활용하도록 설계되었다. 요소를 수집하면서 데이터를 순서대로 읽어가는 동시에, 그 순서를 스택에 배치한다. 스택 최상위의 순서가 머지 기준에 일치하는 경우, 그 순서들은 병합된다. 이는 모든 데이터가 처리될 때까지 계속된다. 다음으로, 모든 순서가 한 번에 2개씩 병합되어, 정렬된 순서는 하나만 남게 된다. 고정 크기의 하위 목록을 병합하는 대신 정렬된 순서를 병합하는 이점은, 전체 리스트를 정렬하기 위해 필요한 비교의 총 수가 감소한다는 것이다.[1]각 순서에는 입력의 크기에 기초한 최소 크기가 있으며, 알고리즘 시작 시 정의된다. 순서가 이 최소 순서 크기보다 작은 경우, 삽입 정렬을 사용하여, 최소 순서 크기에 도달할 때까지 순서에 요소를 추가한다.[1]
2. 5. 갤로핑 모드 (Galloping Mode)


실행 R1과 R2의 병합 과정에서 연속으로 선택된 요소의 수를 기록한다. 이 숫자가 ''최소 갤럽 임계값''(''min_gallop'')에 도달하면, 팀소트는 해당 실행에서 많은 연속된 요소가 계속 선택될 가능성이 있다고 판단하여 갤로핑 모드로 전환한다. R1이 갤로핑 모드를 시작했다고 가정하면, 알고리즘은 다음 두 단계를 거쳐 R2의 다음 요소 ''x''가 삽입될 R1의 위치를 찾는다.
# R1[2''k−1'' − 1] < x ≤ R1[2''k'' − 1]이 되는 ''k''를 지수 검색(갤럽 검색이라고도 함)을 통해 찾는다. 즉, R1에서 2''k−1'' − 1개의 연속된 요소로 구성된 범위를 찾는다.
# 이 범위에 대해 이진 검색을 수행하여 R1에서 ''x''의 정확한 위치를 찾는다.
갤로핑 모드는 실행에서 요소 간의 간격 패턴에 병합 알고리즘을 적응시키려는 시도이다.
하지만 갤로핑이 항상 효율적인 것은 아니다. 경우에 따라 갤로핑 모드는 간단한 선형 검색보다 더 많은 비교를 필요로 할 수 있다. 개발자들의 벤치마크에 따르면, 갤로핑은 한 실행의 초기 요소가 다른 실행의 처음 7개 요소 중 하나가 아닌 경우에만 유용하다. 이를 위해 초기 임계값을 7로 설정한다.
갤로핑 모드의 단점을 보완하기 위해 다음과 같은 두 가지 방법을 사용한다.
- 갤로핑이 이진 검색 알고리즘보다 덜 효율적인 것으로 밝혀지면 갤로핑 모드를 종료한다.
- 갤로핑의 성공 또는 실패를 기반으로 ''min_gallop'' 값을 조정한다. 선택된 요소가 이전에 요소를 반환했던 배열과 동일한 배열에서 온 경우, ''min_gallop''을 1 감소시켜 갤로핑 모드로 다시 전환하도록 유도한다. 그렇지 않으면 값을 1 증가시켜 갤로핑 모드로의 복귀를 억제한다.
임의의 데이터에서는 ''min_gallop'' 값이 매우 커져서 갤로핑 모드가 다시 발생하지 않는 경우가 많다.[15]
2. 6. 내림차순 런 처리
팀소트는 엄격하게 내림차순으로 정렬된 런을 발견하면 이를 뒤집어서 오름차순 런으로 만든 후 런 스택에 추가한다.[1] 동일한 요소를 가진 런을 제외하면 알고리즘의 안정성이 유지된다.[1] 즉, 동일한 요소는 뒤집히지 않는다.[1]3. 분석
팀소트는 n개의 요소를 가진 배열을 정렬할 때 최악의 경우 번의 비교를 수행한다. 최선의 경우, 즉 입력이 이미 정렬된 경우에는 선형 시간 내에 실행되므로 적응형 정렬 알고리즘이다.[1]
이 알고리즘은 객체 참조 또는 포인터를 정렬하는 데 퀵 정렬보다 우수하다. 이는 데이터에 접근하고 비교를 수행하기 위해 비용이 많이 드는 메모리 간접 참조가 필요하며, 퀵 정렬의 캐시 일관성 이점이 크게 줄어들기 때문이다.[1]
4. 장점 및 활용
팀소트는 n개의 요소를 가진 배열을 정렬할 때 최악의 경우 번의 비교가 필요하다. 입력이 이미 정렬된 최상의 경우에는 선형 시간 안에 실행되는데, 이는 팀소트가 적응형 정렬 알고리즘이기 때문이다.[1]
객체 참조 또는 포인터 정렬의 경우 퀵 정렬보다 유리하다. 이는 데이터에 접근하여 비교를 수행하기 위해 비용이 많이 드는 메모리 간접 참조를 필요로 하며, 퀵 정렬의 캐시 일관성 이점이 크게 감소하기 때문이다.[1]
5. 한계 및 형식 검증
2015년, EU FP7 ENVISAGE 프로젝트의 네덜란드 및 독일 연구진은 팀소트의 표준 구현에서 버그를 발견했다.[16] 이 문제는 같은 해 파이썬, 자바, 안드로이드에서 수정되었다.
구체적으로, 쌓인 런 크기에 대한 불변량은 필요한 스택의 최대 크기에 대한 엄격한 상한을 보장한다. 구현은 264 바이트의 입력을 정렬할 수 있을 만큼 충분한 스택을 미리 할당했고, 추가적인 오버플로 검사는 생략했다.
그러나 이 보장은 세 개의 연속된 런의 ''모든'' 그룹에 불변량이 적용되어야 하지만, 구현은 상위 세 개에 대해서만 이를 확인했다.[16] KeY 도구를 사용하여 자바 소프트웨어의 형식 검증을 수행한 연구자들은 이 검사가 충분하지 않다는 것을 발견했으며, 상위 스택이 병합된 후 스택의 더 깊은 곳에서 불변량이 위반되는 런 길이(및 해당 런 길이를 생성하는 입력)를 찾을 수 있었다.[17]
결과적으로, 특정 입력에 대해 할당된 크기는 병합되지 않은 모든 런을 저장하기에 충분하지 않았다. 자바에서, 이러한 입력에 대해 배열 인덱스 초과 예외가 발생한다. 자바 및 안드로이드 v7에서 이 예외를 발생시키는 가장 작은 입력 크기는 67108864 (226)이다. (이전 안드로이드 버전은 이미 65536 (216) 크기의 특정 입력에 대해 이 예외를 발생시켰다.)
자바 구현은 업데이트된 최악의 경우 분석을 기반으로 미리 할당된 스택의 크기를 늘려 수정되었다. 또한 이 기사에서는 스택의 ''네'' 개의 최상위 런이 위의 두 규칙을 만족하는지 확인하여 형식적 방법을 통해 의도된 불변량을 어떻게 설정하는지 보여주었다. 이 접근 방식은 파이썬[18]에서 Python 3.11 릴리스와 함께 2022년에 Powersort로 전환하기 전까지 사용되었다.
참조
[1]
웹사이트
"[Python-Dev] Sorting"
http://mail.python.o[...]
2002-07-20
[2]
서적
"[DROPS]"
http://drops.dagstuh[...]
2018-09-01
[3]
학회
Patience is a Virtue: Revisiting Merge and Sort on Modern Processors
[4]
서적
Nearly-Optimal Mergesorts: Fast, Practical Sorting Methods That Optimally Adapt to Existing Runs
Schloss Dagstuhl – Leibniz-Zentrum für Informatik
2018
[5]
웹사이트
Python Now Uses Powersort
https://www.i-progra[...]
2024-06-21
[6]
웹사이트
"[#JDK-6804124] (coll) Replace "modified mergesort" in java.util.Arrays.sort with timsort"
https://bugs.openjdk[...]
2014-06-11
[7]
웹사이트
Class: java.util.TimSort
[8]
웹사이트
liboctave/util/oct-sort.cc
http://hg.savannah.g[...]
2013-02-18
[9]
웹사이트
Getting things sorted in V8 · V8
https://v8.dev/blog/[...]
2018-12-21
[10]
웹사이트
Is sort() stable in Swift 5?
https://forums.swift[...]
2019-07-04
[11]
웹사이트
slice - Rust
https://doc.rust-lan[...]
2022-12-08
[12]
서적
Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms
https://dl.acm.org/d[...]
1993-01
[13]
웹사이트
listsort.txt
https://hg.python.or[...]
2022-05-18
[14]
웹사이트
Understanding timsort, Part 1: Adaptive Mergesort
http://www.drmaciver[...]
2010-01-11
[15]
웹사이트
listsort.txt
https://github.com/p[...]
2019-12-05
[16]
서적
Computer Aided Verification
http://envisage-proj[...]
2015-07
[17]
웹사이트
Proving that Android's, Java's and Python's sorting algorithm is broken (and showing how to fix it)
http://envisage-proj[...]
2015-02-24
[18]
문서
Python Issue Tracker – Issue 23515: Bad logic in timsort's merge_collapse
http://bugs.python.o[...]
[19]
웹사이트
"[Python-Dev] Sorting"
http://mail.python.o[...]
2011-02-24
[20]
웹사이트
"[DROPS]"
http://drops.dagstuh[...]
2018-09-01
[21]
학회
Patience is a Virtue: Revisiting Merge and Sort on Modern Processors
[22]
웹사이트
"[#JDK-6804124] (coll) Replace "modified mergesort" in java.util.Arrays.sort with timsort"
https://bugs.openjdk[...]
2014-06-11
[23]
웹사이트
Class: java.util.TimSort
[24]
웹사이트
liboctave/util/oct-sort.cc
http://hg.savannah.g[...]
2013-02-18
[25]
웹사이트
Getting things sorted in V8 · V8
https://v8.dev/blog/[...]
2018-12-21
[26]
웹사이트
Is sort() stable in Swift 5?
https://forums.swift[...]
2019-07-04
[27]
웹사이트
slice - Rust
https://doc.rust-lan[...]
2020-09-17
[28]
서적
Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms
1993-01
[29]
웹사이트
listsort.txt
http://hg.python.org[...]
2017-02-10
[30]
웹사이트
Understanding timsort, Part 1: Adaptive Mergesort
http://www.drmaciver[...]
2010-01-11
[31]
웹사이트
listsort.txt
https://github.com/p[...]
2019-12-05
[32]
학술저널
OpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case
http://envisage-proj[...]
2015-07
[33]
학술저널
OpenJDK's Java.utils.Collection.sort() Is Broken: The Good, the Bad and the Worst Case
http://envisage-proj[...]
2015-07
[34]
웹사이트
Proving that Android’s, Java’s and Python’s sorting algorithm is broken (and showing how to fix it)
http://envisage-proj[...]
2015-02-24
[35]
문서
Python Issue Tracker – Issue 23515: Bad logic in timsort's merge_collapse
http://bugs.python.o[...]
[36]
웹인용
"[Python-Dev] Sorting"
http://mail.python.o[...]
2011-02-24
[37]
서적
"[DROPS]"
http://drops.dagstuh[...]
2018-09-01
[38]
간행물
Patience is a Virtue: Revisiting Merge and Sort on Modern Processors
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com