기댓값 최대화 알고리즘

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

기댓값 최대화 알고리즘(Expectation-Maximization algorithm, EM 알고리즘)은 통계 모델에서 잠재변수가 존재할 때 최대가능도 또는 최대사후확률을 갖는 모수를 추정하는 반복적인 알고리즘이다. 이 알고리즘은 데이터에 결측치가 있거나, 관측되지 않은 추가 데이터 포인트를 가정하여 모델을 더 단순하게 공식화할 수 있을 때 유용하며, 통계 모델의 수식을 직접적으로 풀 수 없을 때 최대가능도를 구하는 데 사용된다. EM 알고리즘은 1977년 아서 뎀스터, 낸 라드, 도널드 루빈에 의해 제시되었으나, 특수한 경우에 대한 연구는 이미 이전부터 진행되어 왔다.

개요
분야	통계학, 기계 학습, 데이터 마이닝
약자	EM 알고리즘
이름	기댓값 최대화 알고리즘
정의	잠재변수에 의존하는 확률 모델에서 최대가능도 또는 최대사후확률 추정값을 찾는 반복 알고리즘
특징	반복적인 방법으로 E-단계(기댓값 계산)와 M-단계(최대화)를 번갈아 수행
영문이름	expectation–maximization algorithm
활용
분야	혼합 가우시안 분포 추정 다중 선형 회귀 문제 해결 클러스터 분석 음성 인식 인자분석
예시	올드페이스풀 간헐천 데이터의 EM 클러스터링
작동 방식
반복	M단계의 추정값을 다음 E단계에서 잠재변수 분포를 결정하는데 사용
E단계	현재 모수 추정값을 사용하여 로그-가능도의 기댓값을 계산
M단계	E단계에서 계산된 기댓값을 최대화하는 모수를 추정
수학적 기초
기초 이론	커널 머신 편향-분산 트레이드오프 계산 학습 이론 경험적 위험 최소화 오컴 학습 PAC 학습 통계적 학습 이론 바프니크-체르보넨키스 이론
관련 알고리즘
분류	결정 트리 학습 앙상블 학습 k-최근접 이웃 알고리즘 선형 회귀 나이브 베이즈 분류기 인공 신경망 로지스틱 회귀 퍼셉트론 관련 벡터 머신 서포트 벡터 머신
신경망	오토인코더 딥러닝 심층 신경망 순환 신경망 장단기 기억 게이트 순환 장치 제한된 볼츠만 머신 자기 조직화 지도 합성곱 신경망
강화 학습	시간차 학습 Q-러닝 SARSA
이상 감지	k-최근접 이웃 알고리즘 국소 이상치 계수
차원 축소	요인 분석 정준 상관 분석 독립 성분 분석 선형 판별 분석 음이 아닌 행렬 분해 주성분 분석 t-분포 확률적 임베딩
클러스터링	BIRCH 계층적 클러스터링 k-평균 클러스터링 DBSCAN OPTICS 알고리즘 평균 이동
구조적 예측	그래프 모델 베이즈 네트워크 조건부 랜덤 필드 은닉 마르코프 모델
학술지 및 컨퍼런스
학술지 및 컨퍼런스	ECML PKDD 신경 정보 처리 시스템 학회 국제 머신 러닝 학회 국제 학습 표현 학회 국제 인공 지능 합동 학회 머신 러닝 (저널) 머신 러닝 연구 저널

2. 역사

EM 알고리즘은 아서 뎀스터, 낸 레어드(Nan Laird), 그리고 도널드 루빈(Donald Rubin)이 1977년에 발표한 논문에서 설명되고 이름이 붙여졌다.^{[en-3]논문 Maximum Likelihood from Incomplete Data via the EM Algorithm} 그들은 이 방법이 이전의 저자들에 의해 "특별한 상황에서 여러 번 제안되었다"고 지적했다. 가장 초기의 사례 중 하나는 세드릭 스미스의 대립 유전자 빈도를 추정하기 위한 유전자 계수 방법이다.^{[en-4]논문 The estimation of gene frequencies in a random-mating population} 또 다른 방법은 1958년 H.O. 하틀리가 제안했고, 1977년 하틀리와 호킹이 제안했는데, 이는 뎀스터-레어드-루빈 논문의 많은 아이디어가 비롯된 곳이다.^{[en-5]논문 Maximum Likelihood estimation from incomplete data 1958} 또 다른 하나는 1977년에 S.K. Ng, Thriyambakam Krishnan, 그리고 G.J. McLachlan이 제안했다.^{[en-6]서적 The EM Algorithm Springer Berlin Heidelberg 2022-10-15} 하틀리의 아이디어는 모든 그룹화된 이산 분포로 확장될 수 있다. 지수족에 대한 EM 방법의 매우 자세한 처리는 페르 마틴-뢰프(Per Martin-Löf) 및 안데르스 마틴-뢰프(Anders Martin-Löf)와의 공동 연구에 따라 롤프 순드베리가 그의 학위 논문과 여러 논문에서 발표했다.^{[en-7]논문 Maximum likelihood theory for incomplete data from an exponential family}^{[en-8]학위논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University 1971}^{[en-9]논문 An iterative method for solution of the likelihood equations for incomplete data from exponential families}^{[en-10]기타}^{[en-11]기타 Statistics from the point of view of statistical mechanics Mathematical Institute, Aarhus University 1966}^{[en-12]기타 Statistiska Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Lecture notes 1969-1970), with the assistance of Rolf Sundberg. Stockholm University 1970} 1977년의 뎀스터-레어드-루빈 논문은 이 방법을 일반화했고 더 광범위한 문제에 대한 수렴 분석을 스케치했다. 뎀스터-레어드-루빈 논문은 EM 방법을 통계 분석의 중요한 도구로 확립했다. Meng과 van Dyk (1997)도 참고하라.

뎀스터-레어드-루빈 알고리즘의 수렴 분석에는 결함이 있었고, 올바른 수렴 분석은 1983년 C. F. 제프 우(C. F. Jeff Wu)에 의해 발표되었다.^{[en-15]논문 On the Convergence Properties of the EM Algorithm 1983-03} 우의 증명은 뎀스터-레어드-루빈이 주장한 대로 EM 방법의 수렴이 지수족 외부에서도 성립함을 입증했다.^{[en-15]논문 On the Convergence Properties of the EM Algorithm 1983-03}

원래 EM 알고리즘에서는 기댓값 평가 시 잠재 변수가 취할 수 있는 모든 값을 열거해야 했기 때문에 효율적으로 다룰 수 있는 분포가 제한되었다. 그러나 이후 마르코프 연쇄 몬테카를로법과 변분 베이즈법이 고안됨에 따라 보다 일반적인 분포에서도 현실적인 시간 내에 계산이 가능해졌다. 기댓값 최대화 알고리즘은 1977년 아서 뎀스터, 낸 라드와 도널드 루빈에 의해 제시되었지만, 특수한 경우에서의 기댓값 최대화 알고리즘은 이미 몇몇 저자들에 의해 연구되고 있었고, 특히 롤프 순드베리는 페르 마틴-뢰프, 앤더스 마틴-뢰트와 함께 지수족에 한정된 기댓값 최대화 알고리즘에 관한 연구를 한 바 있다. 1977년 뎀스터-라드-루빈 논문은 이 방법을 일반화하여 지수족뿐만 아니라 다양한 확률분포에 한해서도 알고리즘이 수렴함을 밝혔다. 왕립통계협회저널에 게재된 이 논문은 그 혁신성으로 인해 롤프 순드베리를 비롯한 여럿에게 극찬을 받았으며, 기댓값 최대화 알고리즘을 통계분석의 중요한 도구로 자리매김하게 하였다.

이후 뎀스터-라드-루빈 논문의 알고리즘 수렴성 분석에 오류가 발견되었고, 1983년 C.F. 제프 우에 의해 옳은 증명이 제시되었다. 제프 우의 증명은 기댓값 최대화 알고리즘이 지수족뿐만 아니라 다른 확률분포에도 성립함을 보였다.

3. 서론

EM 알고리즘은 통계 모델에서 (지역) 최대 가능도 매개변수를 찾을 때 사용되며, 이때 방정식이 직접적으로 풀리지 않는 경우가 많다. 이러한 모델은 알려지지 않은 매개변수와 알려진 데이터 관찰 외에도 잠재 변수를 포함하는 것이 일반적이다. 즉, 데이터에 결측값이 있거나, 관찰되지 않은 추가 데이터 포인트를 가정하여 모델을 단순화할 수 있다. 예를 들어, 혼합 모델은 각 관찰된 데이터 포인트에 해당 데이터 포인트가 속한 혼합 성분을 지정하는 관찰되지 않은 데이터 포인트 또는 잠재 변수가 있다고 가정하여 더 간단하게 설명할 수 있다.

최대 가능도 해를 찾기 위해서는 모든 알 수 없는 값, 즉 매개변수와 잠재 변수에 대해 가능도 함수의 미분을 구하고 결과 방정식을 동시에 풀어야 한다. 그러나 잠재 변수가 있는 통계 모델에서는 이것이 일반적으로 불가능하다. 대신, 매개변수에 대한 해를 구하려면 잠재 변수의 값이 필요하고, 그 반대의 경우도 마찬가지인, 서로 얽힌 방정식 집합이 생성된다. 이러한 방정식들은 한 방정식 집합을 다른 방정식 집합에 대입하면 풀 수 없는 형태로 나타난다.

EM 알고리즘은 이러한 두 방정식 집합을 수치적으로 풀 수 있다는 점에서 시작된다. 두 집합의 미지수 중 하나에 임의의 값을 선택하고, 이를 사용하여 두 번째 집합을 추정한 다음, 이러한 새로운 값을 사용하여 첫 번째 집합의 더 나은 추정값을 찾는다. 이 과정을 결과 값이 모두 고정점으로 수렴할 때까지 반복한다. 이러한 반복적인 접근 방식이 수렴할 것이라는 보장은 없지만, 특정 상황에서는 수렴함을 증명할 수 있다. 또한, 수렴점에서 가능도의 미분이 0에 가까워짐을 보일 수 있으며, 이는 해당 지점이 지역 최대값 또는 안장점임을 의미한다.^{[en-15]논문 On the Convergence Properties of the EM Algorithm 1983-03} 일반적으로, 여러 개의 최대값이 발생할 수 있으며, 전역 최대값이 발견된다는 보장은 없다. 일부 가능도에는 특이점 즉, 무의미한 최대값이 존재한다. 예를 들어, 혼합 모델에서 EM 알고리즘에 의해 발견될 수 있는 "해" 중 하나는 구성 요소 중 하나를 0 분산을 갖도록 설정하고, 해당 구성 요소의 평균 매개변수를 데이터 포인트 중 하나와 같게 설정하는 것이다. 기대값-최대화(EM) 기반 알고리즘의 수렴에는 일반적으로 모든 알 수 없는 매개변수(최적화 변수라고 함)에 대한 가능도 함수의 연속성이 필요하다.^{[en-16]논문 Convergence of Expectation-Maximization Algorithm With Mixed-Integer Optimization 2024-04-24}

관찰된 데이터 집합 $\mathbf{X}$ , 관찰되지 않은 잠재 데이터 또는 결측값 $\mathbf{Z}$ 집합, 그리고 미지의 매개변수 벡터 $\boldsymbol\theta$ 와 함께 가능도 함수 $L(\boldsymbol\theta; \mathbf{X}, \mathbf{Z}) = p(\mathbf{X}, \mathbf{Z}\mid\boldsymbol\theta)$ 를 생성하는 통계 모형이 주어졌을 때, 미지의 매개변수의 최대 가능도 추정 (MLE)은 관측된 데이터의 주변 가능도를 최대화하여 결정된다.

: $L(\boldsymbol\theta; \mathbf{X}) = p(\mathbf{X}\mid\boldsymbol\theta) = \int p(\mathbf{X},\mathbf{Z} \mid \boldsymbol\theta) \, d\mathbf{Z} = \int p(\mathbf{X} \mid \mathbf{Z}, \boldsymbol\theta) p(\mathbf{Z} \mid \boldsymbol\theta) \, d\mathbf{Z}$

그러나 $\mathbf{Z}$ 는 관측되지 않았고 $\mathbf{Z}$ 의 분포는 $\boldsymbol\theta$ 를 얻기 전에는 알 수 없기 때문에 이 양을 다루는 것은 종종 어렵다.

EM이 적용되는 일반적인 모델에서 $\mathbf{Z}$ 는 일련의 그룹 중 하나의 멤버십을 나타내는 잠재 변수로 사용된다.

관찰된 데이터 포인트 $\mathbf{X}$ 는 이산형(유한하거나 셀 수 있는 무한 집합에서 값을 취함)이거나 연속형(셀 수 없는 무한 집합에서 값을 취함)일 수 있다. 각 데이터 포인트에는 관찰 벡터가 연결될 수 있다.

결측값(잠재 변수) $\mathbf{Z}$ 는 고정된 수의 값에서 도출된 이산형이며, 관찰된 단위당 하나의 잠재 변수가 있다.

매개변수는 연속형이며, 모든 데이터 포인트와 연결된 매개변수와 잠재 변수의 특정 값과 연결된 매개변수(즉, 해당 잠재 변수가 해당 값을 갖는 모든 데이터 포인트와 연결됨)의 두 가지 종류가 있다.

그러나 다른 종류의 모델에도 EM을 적용할 수 있다.

매개변수 $\boldsymbol\theta$ 의 값을 알고 있다면, 잠재 변수 $\mathbf{Z}$ 의 값은 $\mathbf{Z}$ 의 모든 가능한 값에 대해 로그-우도를 최대화하거나, 은닉 마르코프 모델의 비터비 알고리즘과 같은 알고리즘을 통해 찾을 수 있다. 반대로, 잠재 변수 $\mathbf{Z}$ 의 값을 알고 있다면 매개변수 $\boldsymbol\theta$ 의 추정값을 비교적 쉽게 찾을 수 있다. 일반적으로 관찰된 데이터 포인트를 연결된 잠재 변수의 값에 따라 그룹화하고, 각 그룹에서 포인트의 값 또는 값의 함수를 평균하여 찾을 수 있다. 이는 $\boldsymbol\theta$ 와 $\mathbf{Z}$ 모두 알 수 없는 경우 반복 알고리즘을 제시한다.

1. 먼저 매개변수 $\boldsymbol\theta$ 를 임의의 값으로 초기화한다.

2. $\boldsymbol\theta$ 가 주어졌을 때 $\mathbf{Z}$ 의 가능한 각 값의 확률을 계산한다.

3. 그런 다음, 계산된 $\mathbf{Z}$ 값을 사용하여 매개변수 $\boldsymbol\theta$ 에 대한 더 나은 추정값을 계산한다.

4. 수렴할 때까지 2단계와 3단계를 반복한다.

이 알고리즘은 비용 함수의 국소 최소값에 단조롭게 접근한다.

두 개의 값 , 를 취하는 확률 분포가 있고, 그 확률 분포의 확률 밀도 함수 $p(x,z|\theta)$ 가 미지의 모수 $\theta\in\mathbb{R}^m$ 에 의해 파라미터화된다고 하자. 여기서 $\mathbb{R}$ 은 실수 전체의 집합을 나타낸다.

그리고 $p(x,z|\theta)$ 에 따라 표본 $(x_1,z_1),\ldots,(x_n,z_n)$ 을 독립적으로 추출했지만, $Z=(z_1,\ldots,z_n)$ 의 값은 관측할 수 없고, $X=(x_1,\ldots,x_n)$ 만 관측할 수 있다고 가정한다. 실제 응용에서는 예를 들어, $\theta=(\theta_1,\theta_2)$ 라는 형태를 취하고, 먼저 관측 불가능한 $z_i\sim p_1(z|\theta_1)$ 이 선택된 후, $z_i$ 에 의존하여 관측 가능한 $x_i\sim p_2(x|\theta_2,z_i)$ 가 선택되는 것과 같은 경우에 EM 알고리즘이 사용되는 경우가 많지만, 반드시 이 경우에 해당하지 않아도 된다.

간단하게 하기 위해 기호를 혼용하여 , 의 동시 확률 분포의 확률 밀도 함수도 $p(X,Z|\theta)$ 라고 쓴다. 이하에서는 가 이산 변수인 경우에 대해 설명하지만, 가 연속 변수인 경우도 총합을 적분으로 바꾸는 것 외에는 마찬가지이다.^{[ja-1]서적 PRML}

이러한 상황에서 모수 를 최우도 추정하는 것이 목표이다. 하지만 를 모르는 경우의 $X=(x_1,\ldots,x_n)$ 에 대한 로그 우도

: $\ell(\theta|X):=\log p(X|\theta)=\log \sum_Zp(X,Z|\theta)$

의 최대값을 직접 계산하는 것은 일반적으로 간단하지 않다.

EM 알고리즘은 반복법에 의해 수열 $\hat{\theta}^{(t)}$ 에서 로그 우도 $\ell(\hat{\theta}^{(t)}|X)$ 가 단조 비감소인 것을 만드는 알고리즘이다. 최우도 추정량을 $\hat{\theta}_{\mathrm{MLE}}$ 라고 하면,

: $\ell(\hat{\theta}_{\mathrm{MLE}}|X)\ge \ell(\hat{\theta}^{(t)}|X)$

이므로, $\ell(\hat{\theta}_{\mathrm{MLE}}|X)$ 가 유한하면 $\ell(\hat{\theta}^{(t)}|X)$ 의 단조성에 의해 $\ell(\hat{\theta}^{(t)}|X)$ 는 반드시 수렴한다.

EM 알고리즘에서 구하고자 하는 것은 $X=(x_1,\ldots,x_n)$ 를 관측했을 때의 로그 우도

: $\ell(\theta|X):=\log p(X|\theta)$

를 최대화하는 모수 $\theta$ 이다. EM 알고리즘의 동작 원리를 설명하기 위해 다음과 같은 범함수를 고려한다.

: $\mathcal{L}(q,\theta):=\sum_Z q(Z) \log {p(X,Z|\theta)\over q(Z)}$ 　　...()

여기서 $q(Z)$ 는 임의의 확률 밀도 함수이다. $p_{X,\theta}(Z):=p(Z|X,\theta)$ 라고 하면, $p(Z|X,\theta) p(X|\theta) = p(X,Z|\theta)$ 로부터, 쿨백-라이블러 발산

: $\mathrm{KL}(q||p_{X,\theta})=-\sum_Z q(Z)\log{p(Z|X,\theta) \over q(Z)}$

를 사용하여

: $\mathcal{L}(q,\theta)=\ell(\theta|X)-\mathrm{KL}(q||p_{X,\theta})$ 　...()

로 쓸 수 있다는 것을 알 수 있다. 쿨백-라이블러 발산이 항상 음수가 아니라는 사실로부터,

: $\ell(\theta|X)\ge\mathcal{L}(q,\theta)$

이므로, $\mathcal{L}(q,\theta)$ 는 $\ell(\theta|X)$ 의 하한이 된다. EM 알고리즘은 이 하한 $\mathcal{L}(q,\theta)$ 를 점진적으로 개선해 나감으로써 $\ell(\theta|X)$ 를 가능한 한 최대화하는 알고리즘이다. 즉, E 단계와 M 단계는 다음과 같이 바꿔 쓸 수 있다^{[ja-1]서적 PRML}:

'''E 단계''': $\hat{q}^{(t)} = \underset{q}{\operatorname{arg\,max}} \mathcal{L}(q,\hat{\theta}^{(t)})$ 를 구한다.
'''M 단계''': $\hat{\theta}^{(t+1)} = \underset{\theta}{\operatorname{arg\,max}}\mathcal{L}(\hat{q}^{(t)},\theta)$ 를 구한다.

이 사실로부터 로그 우도

\ell(\hat{\theta}^{(t)}|X)

의 단조 비감소성이 분명히 따른다.

(단, 반복법의 일반적인 특성으로, 초기값에 따라서는 우도의 최대점이 아닌 극대점에 도달하여 멈출 가능성이 있다.)

기댓값 최대화 알고리즘은 통계 모델의 수식을 정확히 풀 수 없을 때 최대가능도를 구하는 데 사용된다. 이런 통계 모델은 대개 잠재변수와 관측할 수 없는 모수, 관측된 데이터로 구성되어 있고, 몇몇 관측값들이 누락되어 있거나 관측되지 않은 데이터가 존재한다고 가정할 수도 있다. 예를 들면, 혼합 모델에서 매 관측값이 그에 상응하는 잠재변수 혹은 관측되지 않은 값을 가지고 있다고 가정할 수 있다.

최대가능도는 관측되지 않은 모든 변수 각각에 대하여 로그가능도를 미분한 식을 풀어서 구할 수 있다. 하지만 잠재변수를 포함하는 통계 모델의 수식들은 매우 복잡하여 이와 같은 방법으로는 풀 수 없다. 각각의 변수에 관해 미분한 식은 서로 얽혀있어 한 수식의 해를 구하기 위해서는 다른 식의 해를 구해야 하는데, 이 수식의 해 또한 이전 식의 변수를 포함하기 때문이다. 따라서 이 경우 정확한 해를 계산하는 것은 불가능하다.

하지만 기댓값 최대화 알고리즘을 이용하면 이 문제의 해를 수치적으로 계산할 수 있다. 우선 서로 얽혀있는 두 식과 각각의 변수들을 가정해보자. 두 식은 얽혀있기 때문에 한 식의 변수는 다른 식의 변수일 수 있다. 첫 번째 식의 변수값을 임의로 잡은 후 이 변수값으로 두 번째 식의 변수값을 추정한다. 그렇게 구한 변수값으로 다시 첫 번째 식의 변수값을 추정하고 이를 반복한다. 특정한 상황에서 충분히 많은 반복을 거치면 각각의 변수들이 일정한 값으로 수렴한다는 것을 보일 수 있다. 또한, 이 값에서 로그가능도의 미분은 0이 됨을 보일 수 있고, 이는 이 값이 극점이거나 안장점임을 의미한다. 일반적으로 로그가능도는 여러 개의 극점을 가질 수 있으므로 기댓값 최대화 알고리즘이 반드시 최댓값을 구할 수는 없다. 어떤 가능도는 특이점, 즉 무의미한 극점을 갖기도 한다. 예를 들어, 혼합 모델에서 한 성분의 평균 매개변수를 관측된 하나의 데이터로 놓고 분산 변수를 0으로 설정할 때 발생하는 특이점이 기댓값 최대화 알고리즘으로 구해지는 해가 될 수 있다.

4. 방식

EM 알고리즘은 주변 우도(marginal likelihood)의 최대 우도 추정값을 찾기 위해 다음 두 단계를 반복적으로 적용한다.

기댓값 계산 단계 (E 단계): $Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)})$ 를 $\mathbf{X}$ 와 현재 매개변수 추정값 $\boldsymbol\theta^{(t)}$ 가 주어졌을 때, $\mathbf{Z}$ 의 현재 조건부 분포에 대한 $\boldsymbol\theta$ 의 로그 우도 함수의 기댓값으로 정의한다.

:

Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z} \sim p(\cdot | \mathbf{X},\boldsymbol\theta^{(t)})}\left[ \log p (\mathbf{X},\mathbf{Z} | \boldsymbol\theta) \right] \,

최대화 단계 (M 단계): 이 양을 최대화하는 매개변수를 찾는다.

:

\boldsymbol\theta^{(t+1)} = \underset{\boldsymbol\theta}{\operatorname{arg\,max}} \ Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) \,

이를 하나의 방정식으로 표현하면 다음과 같다.

:

\boldsymbol\theta^{(t+1)} = \underset{\boldsymbol\theta}{\operatorname{arg\,max}}\operatorname{E}_{\mathbf{Z} \sim p(\cdot | \mathbf{X},\boldsymbol\theta^{(t)})}\left[ \log p (\mathbf{X},\mathbf{Z} | \boldsymbol\theta) \right] \,

EM 알고리즘은 수열

\hat{\theta}^{(0)},\hat{\theta}^{(1)},\ldots

를 다음과 같이 생성한다.^{[ja-1]서적 PRML}

1. 초기값

\hat{\theta}^{(0)}

를 선택한다.

2.

t=0,1,\ldots

에 대해 다음을 반복한다.

E 스텝: $p(Z|X,\hat{\theta}^{(t)})$ 를 구한다.
M 스텝: $\hat{\theta}^{(t+1)} = \underset{\theta} {\operatorname{arg\,max}} \ Q(\theta|\hat{\theta}^{(t)}) \,$ 를 구한다.

여기서 ''Q''는 대수우도 함수

\log p (X,Z|\theta)

의 ''Z''에 관한 조건부 기댓값이다.

:

Q(\theta|\theta^{(t)}):= \operatorname{E}_{Z|X,\hat{\theta}^{(t)}}\big[ \log p(X,Z|\theta)  \big] =\sum_Z p(Z|X,\hat{\theta}^{(t)}) \log p (X,Z|\theta) \,

실제 응용에서는

\hat{\theta}^{(t)}

의 값이 충분히 작아졌다고 판단되는 조건을 설정하고, 해당 조건을 충족하면 루프를 종료한다. 루프 종료 조건은 파라미터 값이나 대수우도 함수를 사용해서 정한다.^{[ja-1]서적 PRML}

관측 가능한 확률변수

\mathbf{X}

, 관측 불가능한 확률변수

\mathbf{Z}

, 모수

\boldsymbol{\theta}

가 있을 때,

(\mathbf{X}, \mathbf{Z})

에 대한 확률분포는

L (\boldsymbol\theta;\mathbf{X},\mathbf{Z}) = p(\mathbf{X}, \mathbf{Z}|\boldsymbol{\theta})

로 주어진다. 최대가능도를 계산하려는 경우, 최대화하려는 가능도 함수는

L(\boldsymbol{\theta}; \mathbf{X}) = p(\mathbf{X} |\boldsymbol{\theta}) = \sum_{\mathbf{Z}} p(\mathbf{X}, \mathbf{Z}|\boldsymbol{\theta})

로 정의할 수 있다.

이 수식의 계산 비용은 잠재변수

\mathbf{Z}

가 가질 수 있는 값의 수에 비례하며,

\mathbf{Z}

의 차원이 증가할수록 값의 수는 지수적으로 증가하므로 계산이 매우 어렵다.

기댓값 최대화 알고리즘은 다음 두 단계를 반복하여 가능도 함수

L(\boldsymbol{\theta}; \mathbf{X})

의 최대가능도를 구한다.

기댓값 (E) 단계: $\boldsymbol{\theta}^{(t)}$ 가 주어지고 새로운 $\boldsymbol{\theta}$ 를 사용할 때 가능도의 기댓값 $Q$ 를 정의한다. 이때 기댓값을 취하는 확률분포는 $\mathbf{X}$ , $\boldsymbol{\theta}^{(t)}$ 가 주어졌을 때 $\mathbf{Z}$ 의 조건부 분포이다.

:

Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) = \operatorname{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}}\left[ \log L (\boldsymbol\theta;\mathbf{X},\mathbf{Z})  \right] = \sum_{\mathbf{Z}} p(\mathbf{Z}|\mathbf{X}, \boldsymbol{\theta}^{(t)}) \log L(\boldsymbol\theta;\mathbf{X},\mathbf{Z})

최대화 (M) 단계: $Q$ 를 최대화하는 새로운 모수 $\boldsymbol\theta^{(t+1)}$ 를 계산한다.

:

\boldsymbol\theta^{(t+1)} = \underset{\boldsymbol\theta}{\operatorname{arg\,max}} \ Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) \,

기댓값 최대화 알고리즘이 적용되는 모델은 일반적으로 다음 성질을 만족한다.

관측값 $\mathbf{X}$ 는 이산적이거나 연속적이다.
누락값/잠재변수 $\mathbf{Z}$ 는 이산적이며, 각각의 관측값은 하나의 잠재변수를 가진다.
모수는 연속적이며, 관측값과 관련된 모수 또는 잠재변수의 값에 대응하는 모수로 나뉜다.

모수

\boldsymbol{\theta}

가 주어졌을 때, 잠재변수

\mathbf{Z}

에 관한 가능도 함수를 최대화하여

\mathbf{Z}

값을 쉽게 추정할 수 있으며, 반대로 잠재변수

\mathbf{Z}

값이 주어졌을 때, 모수에 관한 가능도 함수를 최대화하여 모수

\boldsymbol{\theta}

값을 추정할 수 있다. 모수와 잠재변수 중 하나의 값을 알면 다른 값을 쉽게 알 수 있다는 것이 기댓값 최대화 알고리즘의 핵심이다. 알고리즘을 요약하면 다음과 같다.

1. 모수

\boldsymbol{\theta}

를 임의의 값으로 설정한다.

2. 주어진 모수 값에 대한 잠재변수

\mathbf{Z}

값을 추정한다.

3. 2단계에서 얻은 잠재변수 값을 이용하여 모수

\boldsymbol{\theta}

값을 다시 추정한다.

4. 모수

\boldsymbol{\theta}

값과 잠재변수

\mathbf{Z}

값이 수렴할 때까지 2, 3단계를 반복한다.

이 알고리즘은 비용함수의 극대점으로 단조 수렴한다.

기댓값 최대화 알고리즘은 극대점을 찾기 때문에, 실제 최대점이 아닐 수 있다. 이를 피하기 위해 여러 개의 임의 초기값에 대해 계산하거나 담금질 기법 등을 사용할 수 있다.

4. 1. 기댓값 (E) 단계

관측된 데이터 집합

\mathbf{X}

, 관측되지 않은 잠재 데이터 또는 결측값

\mathbf{Z}

집합, 그리고 미지의 매개변수 벡터

\boldsymbol\theta

와 함께 가능도 함수

L(\boldsymbol\theta; \mathbf{X}, \mathbf{Z}) = p(\mathbf{X}, \mathbf{Z}\mid\boldsymbol\theta)

를 생성하는 통계 모형이 주어졌을 때, 미지의 매개변수의 최대 가능도 추정 (MLE)은 관측된 데이터의 주변 가능도를 최대화하여 결정된다.

:

L(\boldsymbol\theta; \mathbf{X}) = p(\mathbf{X}\mid\boldsymbol\theta) = \int  p(\mathbf{X},\mathbf{Z} \mid \boldsymbol\theta) \, d\mathbf{Z} = \int  p(\mathbf{X} \mid \mathbf{Z}, \boldsymbol\theta) p(\mathbf{Z} \mid \boldsymbol\theta) \, d\mathbf{Z}

그러나

\mathbf{Z}

는 관측되지 않았고

\mathbf{Z}

의 분포는

\boldsymbol\theta

를 얻기 전에는 알 수 없기 때문에 이 양은 종종 다루기 어렵다. EM 알고리즘에서는 다음의 순서에 의해 수열

\hat{\theta}^{(0)},\hat{\theta}^{(1)},\ldots

를 만든다.^{[ja-1]서적 PRML}

초기값 $\hat{\theta}^{(0)}$ 를 (어떠한 방법으로든) 선택한다.
$t=0,1,\ldots$ 에 대해서 다음을 실행한다

E 스텝:

p(Z|X,\hat{\theta}^{(t)})

를 구한다.
M 스텝:

\hat{\theta}^{(t+1)} = \underset{\theta} {\operatorname{arg\,max}} \ Q(\theta|\hat{\theta}^{(t)}) \,

를 구한다.

여기서 ''Q''는 대수우도 함수

\log p (X,Z|\theta)

의 에 관한 조건부 기댓값

:

Q(\theta|\theta^{(t)}):= \operatorname{E}_{Z|X,\hat{\theta}^{(t)}}\big[ \log p(X,Z|\theta)  \big] =\sum_Z p(Z|X,\hat{\theta}^{(t)}) \log p (X,Z|\theta) \,

이다. 실제 응용에서는,

\hat{\theta}^{(t)}

의 값이 충분히 작아졌다고 판정하는 어떠한 조건을 사전에 정해두고, 그 조건을 충족하면 상술한 루프를 종료한다. 루프를 종료하는 조건은, 파라미터 값이나 대수우도 함수를 사용해서 정해진다.^{[ja-1]서적 PRML}

쿨백-라이블러 발산(Kullback-Leibler divergence)

\mathrm{KL}(q||p_{X,\theta})

가 최솟값 0이 되는 경우는

q=p_{\theta,X}

인 경우뿐이었으므로, ()에 따라

\mathcal{L}(q,\theta)

는

:

q(Z)=p(Z|X,\theta)

가 충족되는 경우에 최댓값을 갖는다. 즉, EM 알고리즘에서의 E단계는

\theta=\hat{\theta}^{(t)}

를 고정한 상태에서

\mathcal{L}(q,\theta)

를 최대화하는

q

인

:

\hat{q}^{(t)} := p_{X,\hat{\theta}^{(t)}} = \underset{q}{\operatorname{arg\,max}}\mathcal{L}(q,\hat{\theta}^{(t)})

를 구하는 단계이다.

4. 2. 최대화 (M) 단계

EM 알고리즘은 다음과 같은 순서로 수열

\hat{\theta}^{(0)},\hat{\theta}^{(1)},\ldots

를 생성한다.^{[ja-1]서적 PRML}

초기값 $\hat{\theta}^{(0)}$ 를 선택한다.
$t=0,1,\ldots$ 에 대해 다음을 반복한다.
E 단계: $p(Z|X,\hat{\theta}^{(t)})$ 를 계산한다.
M 단계: $\hat{\theta}^{(t+1)} = \underset{\theta} {\operatorname{arg\,max}} \ Q(\theta|\hat{\theta}^{(t)}) \,$ 를 계산한다.

여기서 ''Q''는 대수우도 함수

\log p (X,Z|\theta)

의 에 대한 조건부 기댓값이다.

Q(\theta|\theta^{(t)}):= \operatorname{E}_{Z|X,\hat{\theta}^{(t)}}\big[ \log p(X,Z|\theta)  \big] =\sum_Z p(Z|X,\hat{\theta}^{(t)}) \log p (X,Z|\theta) \,

실제 응용에서는

\hat{\theta}^{(t)}

값의 변화가 충분히 작아졌다고 판단되면 루프를 종료한다. 루프 종료 조건은 파라미터 값이나 대수우도 함수를 사용하여 결정한다.^{[ja-1]서적 PRML}

\mathcal{L}(q,\theta)

의 정의식()에

\hat{q}^{(t)}=p_{X,\hat{\theta}^{(t)}}

를 대입하면,

:

\mathcal{L}(\hat{q}^{(t)},\theta)=\sum_Z p(Z|X,\theta^{(t)})\log {p(X,Z|\theta)\over p(Z|X,\theta^{(t)})}=Q(\theta|\theta^{(t)})-H_{X,\theta^{(t)}}(Z)

가 성립한다. 여기서

H_{X,\theta^{(t)}}(Z)=\textstyle \sum_Z p(Z|X,\theta^{(t)}) \log p(Z|X,\theta^{(t)})

는 조건부 엔트로피이며, 위 식의 우변 두 번째 항은 에 의존하지 않으므로,

:

\hat{\theta}^{(t+1)}= \underset{\theta}{\operatorname{arg\,max}} Q(\theta|\hat{\theta}^{(t)})= \underset{\theta}{\operatorname{arg\,max}} \mathcal{L}(p_{X,\hat{\theta}^{(t)}},\theta)

가 성립한다.

5. 성질

EM 반복은 관측된 데이터의 가능도 함수를 증가시키지만, 그 수열이 최대 가능도 추정으로 수렴한다는 보장은 없다. 다봉 분포의 경우, 이는 EM 알고리즘이 시작 값에 따라 관측된 데이터 가능도 함수의 국소 최대값으로 수렴할 수 있음을 의미한다. 국소 최댓값을 벗어나기 위해 무작위 재시작 언덕 오르기(여러 다른 무작위 초기 추정값 $\boldsymbol\theta^{(t)}$ 으로 시작) 또는 모의 담금질 방법을 적용하는 것과 같은 다양한 경험적 또는 메타휴리스틱 접근 방식이 존재한다.

EM은 가능도가 지수족일 때 특히 유용하다. E 단계는 충분 통계량의 기대값 합이 되고, M 단계는 선형 함수를 최대화하는 것을 포함한다. 이러한 경우, 폐쇄형 표현식을 사용하는 각 단계에 대한 업데이트를 선드베리 공식을 사용하여 도출하는 것이 일반적으로 가능하다.^{[en-8]학위논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University 1971}^{[en-9]논문 An iterative method for solution of the likelihood equations for incomplete data from exponential families}^{[en-11]기타 Statistics from the point of view of statistical mechanics Mathematical Institute, Aarhus University 1966}^{[en-12]기타 Statistiska Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Lecture notes 1969-1970), with the assistance of Rolf Sundberg. Stockholm University 1970}^{[en-13]기타 The notion of redundancy and its use as a quantitative measure of the deviation between a statistical hypothesis and a set of observational data. Aarhus 1973}^{[en-14]논문 The notion of redundancy and its use as a quantitative measure of the discrepancy between a statistical hypothesis and a set of observational data}^{[ko-1]저널 Maximum likelihood theory for incomplete data from an exponential family}^{[ko-2]논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University}^{[ko-3]저널 An iterative method for solution of the likelihood equations for incomplete data from exponential families}^{[ko-4]서적 Contributions to the theory of estimation from grouped and partially grouped samples Almqvist & Wiksell}^{[ko-5]논문 "Utvärdering av livslängder i subnanosekundsområdet" ("Evaluation of sub-nanosecond lifetimes")}^{[ko-6]논문 Statistics from the point of view of statistical mechanics Mathematical Institute, Aarhus University}^{[ko-7]논문 Statistika Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Notes from seminars in the academic year 1969-1970), with the assistance of Rolf Sundberg. Stockholm University}

EM 방법은 뎀스터, 레어드, 루빈의 원 논문에서 베이즈 추론에 대한 최대 사후 확률(MAP) 추정치를 계산하도록 수정되었다.

경사 하강법, 켤레 경사법 또는 가우스-뉴턴 알고리즘의 변형과 같은 최대 가능도 추정치를 찾는 다른 방법이 존재한다. EM과 달리 이러한 방법은 일반적으로 가능도 함수의 1차 및/또는 2차 도함수의 평가를 요구한다.

6. 올바름 증명

기댓값 최대화 알고리즘(Expectation-Maximization algorithm)은 $\log p(\mathbf{X}\mid\boldsymbol\theta)$ 를 직접적으로 향상시키기보다는 $Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)})$ 를 향상시키는 방식으로 작동한다. 여기서 전자를 개선하면 후자가 개선됨을 보인다.^{[en-19]서적 Statistical Analysis with Missing Data John Wiley & Sons}^{[en-20]영어 논문 Inferring neural activity before plasticity as a foundation for learning beyond backpropagation 2024-02}

확률 $p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta)$ 가 0이 아닌 모든 $\mathbf{Z}$ 에 대해 다음을 쓸 수 있다.

: $\log p(\mathbf{X}\mid\boldsymbol\theta) = \log p(\mathbf{X},\mathbf{Z}\mid\boldsymbol\theta) - \log p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta).$

양변에 $p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta^{(t)})$ 를 곱하고 $\mathbf{Z}$ 에 대해 합(또는 적분)하여 현재 매개변수 추정치 $\theta^{(t)}$ 하에서 알 수 없는 데이터 $\mathbf{Z}$ 의 가능한 값에 대한 기댓값을 취한다. 좌변은 상수 기댓값이므로 다음을 얻는다.

: $\begin{align}\log p(\mathbf{X}\mid\boldsymbol\theta) &= \sum_{\mathbf{Z}} p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta^{(t)}) \log p(\mathbf{X},\mathbf{Z}\mid\boldsymbol\theta)$

\sum_{\mathbf{Z}} p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta^{(t)}) \log p(\mathbf{Z}\mid\mathbf{X},\boldsymbol\theta) \\

& = Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) + H(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}),\end{align}

여기서

H(\boldsymbol\theta\mid\boldsymbol\theta^{(t)})

는 대체되는 음의 합으로 정의된다.

이 마지막 방정식은

\boldsymbol\theta = \boldsymbol\theta^{(t)}

를 포함한 모든

\boldsymbol\theta

값에 대해 성립한다.

:

\log p(\mathbf{X}\mid\boldsymbol\theta^{(t)})= Q(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)}) + H(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)}),

그리고 이 마지막 방정식을 이전 방정식에서 빼면 다음을 얻는다.

:

\log p(\mathbf{X}\mid\boldsymbol\theta) - \log p(\mathbf{X}\mid\boldsymbol\theta^{(t)})= Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) - Q(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)})+ H(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) - H(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)}).

그러나 깁스 부등식(Gibbs' inequality)에 따르면

H(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) \ge H(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)})

이므로 다음을 결론 내릴 수 있다.

:

\log p(\mathbf{X}\mid\boldsymbol\theta) - \log p(\mathbf{X}\mid\boldsymbol\theta^{(t)})\ge Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)}) - Q(\boldsymbol\theta^{(t)}\mid\boldsymbol\theta^{(t)}).

다시 말해,

Q(\boldsymbol\theta\mid\boldsymbol\theta^{(t)})

를 개선하도록

\boldsymbol\theta

를 선택하면

\log p(\mathbf{X}\mid\boldsymbol\theta)

가 적어도 그만큼 개선된다.

EM 알고리즘에서 우리가 구하고자 하는 것은

X=(x_1,\ldots,x_n)

를 관측했을 때의 로그 우도

:

\ell(\theta|X):=\log p(X|\theta)

를 최대화하는 모수

\theta

였다. EM 알고리즘의 동작 원리를 설명하기 위해 다음과 같은 범함수를 생각한다:

:

\mathcal{L}(q,\theta):=\sum_Z q(Z) \log {p(X,Z|\theta)\over q(Z)}

　　...^{[ja-1]서적 PRML}

여기서

q(Z)

는 임의의 확률 밀도 함수이다.

p_{X,\theta}(Z):=p(Z|X,\theta)

라고 하면,

p(Z|X,\theta) p(X|\theta) = p(X,Z|\theta)

로부터, 쿨백-라이블러 발산(カルバック・ライブラー情報量)

:

\mathrm{KL}(q||p_{X,\theta})=-\sum_Z q(Z)\log{p(Z|X,\theta) \over q(Z)}

를 사용하여

:

\mathcal{L}(q,\theta)=\ell(\theta|X)-\mathrm{KL}(q||p_{X,\theta})

　...^{[ja-1]서적 PRML}

로 쓸 수 있다는 것을 알 수 있다. 쿨백-라이블러 발산이 항상 음수가 아니라는 사실(깁스 부등식(ギブスの不等式))로부터,

:

\ell(\theta|X)\ge\mathcal{L}(q,\theta)

이므로,

\mathcal{L}(q,\theta)

는

\ell(\theta|X)

의 하한이 된다. EM 알고리즘은 이 하한

\mathcal{L}(q,\theta)

를 점진적으로 개선해 나감으로써

\ell(\theta|X)

를 가능한 한 최대화하는 알고리즘이다. 즉, E 단계와 M 단계는 다음과 같이 바꿔 쓸 수 있음을 나타낼 수 있다^{[ja-1]서적 PRML}:

'''E 단계''': $\hat{q}^{(t)} = \underset{q}{\operatorname{arg\,max}} \mathcal{L}(q,\hat{\theta}^{(t)})$ 를 구한다.
'''M 단계''': $\hat{\theta}^{(t+1)} = \underset{\theta}{\operatorname{arg\,max}}\mathcal{L}(\hat{q}^{(t)},\theta)$ 를 구한다.

이 사실로부터 로그 우도

\ell(\hat{\theta}^{(t)}|X)

의 단조 비감소성이 분명히 따른다.

(단, 반복법의 일반적인 특성으로, 초기값에 따라서는 우도의 최대점이 아닌 극대점에 도달하여 멈출 가능성이 있다.)

본 절에서는 E단계, M단계가 위에서 설명한 것처럼 다시 쓰여질 수 있음을 보인다. 본 절의 증명은 문헌^{[ja-1]서적 PRML}을 참고하였다.

기댓값 최대화 알고리즘은

\log p(\mathbf{X}|\boldsymbol\theta)

을 직접적으로 향상시키기 보다

Q(\boldsymbol\theta|\boldsymbol\theta^{(t)})

를 향상시키는 일이다.

여기에서 증명하는 것은

Q(\boldsymbol\theta|\boldsymbol\theta^{(t)})

를 향상시키는

\boldsymbol\theta

를 찾으면

\log p(\mathbf{X}|\boldsymbol\theta)

가 향상된다는 것이다.^{[ko-10]서적 Statistical Analysis with Missing Data John Wiley & Sons}

확률이 0이 아닌

p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta)

를 만족하는 어떤

\mathbf{Z}

에 대해서, 다음과 같이 이야기할 수 있다:

::

\log p(\mathbf{X}|\boldsymbol\theta) = \log p(\mathbf{X},\mathbf{Z}|\boldsymbol\theta) - \log p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta) \,.

p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)})

를

\mathbf{Z}

에 대해서 합한 값(혹은 적분한 값)을 양변에 곱할 수 있다. 좌변은 상수인 기댓값이므로:

::

\begin{align}\log p(\mathbf{X}|\boldsymbol\theta) &= \sum_{\mathbf{Z}} p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}) \log p(\mathbf{X},\mathbf{Z}|\boldsymbol\theta)

\sum_{\mathbf{Z}} p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta^{(t)}) \log p(\mathbf{Z}|\mathbf{X},\boldsymbol\theta) \\

& = Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) + H(\boldsymbol\theta|\boldsymbol\theta^{(t)}) \,,\end{align}

여기에서,

H(\boldsymbol\theta|\boldsymbol\theta^{(t)})

는 음수의 합(negated sum)으로 정의된다.

마지막 식은

\boldsymbol\theta = \boldsymbol\theta^{(t)}

인 경우를 포함해서 모든

\boldsymbol\theta

에 대해서도 성립한다.

::

\log p(\mathbf{X}|\boldsymbol\theta^{(t)})= Q(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)}) + H(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)}) \,,

이전의 식으로부터 이 마지막 식을 빼면,

::

\log p(\mathbf{X}|\boldsymbol\theta) - \log p(\mathbf{X}|\boldsymbol\theta^{(t)})= Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) - Q(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)})+ H(\boldsymbol\theta|\boldsymbol\theta^{(t)}) - H(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)}) \,,

이다.

하지만, 깁스 부등식(Gibbs' inequality)에 의해서

H(\boldsymbol\theta|\boldsymbol\theta^{(t)}) \ge H(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)})

이다.

그러므로, 우리는 다음 결론에 도달할 수 있다:

::

\log p(\mathbf{X}|\boldsymbol\theta) - \log p(\mathbf{X}|\boldsymbol\theta^{(t)})\ge Q(\boldsymbol\theta|\boldsymbol\theta^{(t)}) - Q(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)}) \,.

그러므로,

Q(\boldsymbol\theta^{(t)}|\boldsymbol\theta^{(t)})

에 비해서

Q(\boldsymbol\theta|\boldsymbol\theta^{(t)})

가 커지도록

\boldsymbol\theta

을 선택하면, 최소한 그 이상으로

\log p(\mathbf{X}|\boldsymbol\theta^{(t)})

에 비해서

\log p(\mathbf{X}|\boldsymbol\theta)

가 향상될 것이다.

7. 대체 설명

EM 알고리즘은 좌표 하강법(coordinate descent)의 한 예로, 두 번의 번갈아 가며 최대화 단계를 거친다.^{[en-21]서적 Learning in Graphical Models MIT Press 2009-03-22}^{[en-22]서적 The Elements of Statistical Learning Springer} 함수 $F(q,\theta) := \operatorname{E}_q [ \log L (\theta ; x,Z) ] + H(q)$ 를 고려할 때, 여기서 ''q''는 관찰되지 않은 데이터 ''z''에 대한 임의의 확률 분포이고, ''H(q)''는 분포 ''q''의 엔트로피(Entropy (information theory))이다. 이 함수는 $F(q,\theta) = -D_{\mathrm{KL}}\big(q \parallel p_{Z\mid X}(\cdot\mid x;\theta ) \big) + \log L(\theta;x)$ 로 쓸 수 있다. 여기서 $p_{Z\mid X}(\cdot\mid x;\theta )$ 는 관찰된 데이터 $x$ 가 주어졌을 때 관찰되지 않은 데이터의 조건부 분포이고, $D_{KL}$ 은 쿨백-라이블러 발산(Kullback–Leibler divergence)이다.

EM 알고리즘의 단계는 다음과 같다.

:''기대 단계'': $F$ 를 최대화하는 $q$ 를 선택한다.

:: $q^{(t)} = \operatorname{arg\,max}_q \ F(q,\theta^{(t)})$

:''최대화 단계'': $F$ 를 최대화하는 $\theta$ 를 선택한다.

:: $\theta^{(t+1)} = \operatorname{arg\,max}_\theta \ F(q^{(t)},\theta)$

쿨백-라이블러 발산(Kullback–Leibler divergence) $\mathrm{KL}(q||p_{X,\theta})$ 가 최솟값 0이 되는 경우는 $q=p_{\theta,X}$ 인 경우뿐이므로, $\mathcal{L}(q,\theta)$ 는 $q(Z)=p(Z|X,\theta)$ 가 충족되는 경우에 최댓값을 갖는다. 즉, EM 알고리즘에서의 E단계는 $\theta=\hat{\theta}^{(t)}$ 를 고정한 상태에서 $\mathcal{L}(q,\theta)$ 를 최대화하는 $q$ 인 $\hat{q}^{(t)} := p_{X,\hat{\theta}^{(t)}} = \underset{q}{\operatorname{arg\,max}}\mathcal{L}(q,\hat{\theta}^{(t)})$ 를 구하는 단계이다.

상황에 따라 기댓값 최대화 알고리즘을 다음의 두 최대화 단계로 보는 것이 편리하다.^{[ko-11]저널 A view of the EM algorithm that justifies incremental, sparse, and other variants MIT Press 2009-03-22}^{[ko-12]서적 The Elements of Statistical Learning Springer} ''q''는 미관측 데이터 ''z''를 나타내는 임의의 확률 분포, ''p''_''Z''|''X''(· |''x'';''θ'')는 관측 데이터 ''x''가 주어졌을 때의 조건부 확률 분포, ''H''는 엔트로피(Entropy (information theory)), 그리고 ''D''_KL는 쿨백-라이블러 발산이라고 할 때, 다음 식을 고려한다.

: $F(q,\theta) = \operatorname{E}_q [ \log L (\theta ; x,Z) ] + H(q) = -D_{\mathrm{KL}}\big(q \big\| p_{Z|X}(\cdot|x;\theta ) \big) + \log L(\theta;x)$

그러면 기댓값 최대화에서의 단계는 다음과 같이 나타낼 수 있다:

:'''기댓값 단계''': ''F''를 최대화하는 ''q''를 찾는다 :

:: $q^{(t)} = \underset{q}\operatorname{arg\,max} \ F(q,\theta^{(t)})$

:'''최대화 단계''': ''F''를 최대화하는 ''θ''를 찾는다:

:: $\theta^{(t+1)} = \underset{\theta}\operatorname{arg\,max} \ F(q^{(t)},\theta)$

8. 적용

EM 알고리즘은 특히 계량 유전학에서 혼합 모형의 모수 추정에 자주 사용된다.^{[en-23]논문 Newton—Raphson and EM Algorithms for Linear Mixed-Effects Models for Repeated-Measures Data}^{[en-24]논문 Fitting Mixed-Effects Models Using Efficient EM-Type Algorithms}^{[en-25]논문 A new REML (parameter expanded) EM algorithm for linear mixed models} 심리 측정학에서 EM 알고리즘은 문항 반응 이론 모형의 문항 모수와 잠재 능력을 추정하는 데 중요한 도구이다. 결측 데이터를 처리하고 식별되지 않은 변수를 관찰하는 능력을 통해 EM은 포트폴리오의 위험을 평가하고 관리하는 데 유용한 도구가 되고 있다. EM 알고리즘(및 더 빠른 변형인 순서화 부분집합 기대값 최대화)은 의료 영상 재구성, 특히 양전자 방출 단층 촬영, 단일 광자 방출 컴퓨터 단층 촬영, 및 X선 컴퓨터 단층 촬영에서 널리 사용된다. 구조 공학에서, 기대값 최대화를 이용한 구조 식별(STRIDE)^{[en-26]논문 “STRIDE for Structural Identification using Expectation Maximization: Iterative Output-Only Method for Modal Identification.” 2016} 알고리즘은 센서 데이터를 사용하여 구조 시스템의 고유 진동 특성을 식별하는 출력 전용 방법이다( 운영 모달 분석 참조). EM은 데이터 클러스터링에도 사용된다. 자연어 처리에서 알고리즘의 두드러진 예는 은닉 마르코프 모형의 바움-웰치 알고리즘과 확률적 문맥 자유 문법의 비지도 유도를 위한 내부-외부 알고리즘이다. 증권 거래소에서 주식의 후속 거래 사이의 시간인 거래 간 대기 시간 분석에서 EM 알고리즘이 매우 유용한 것으로 입증되었다.^{[en-27]논문 Censored expectation maximization algorithm for mixtures: Application to intertrade waiting times 2022} 기댓값 최대화 알고리즘은 기계 학습과 컴퓨터 비전의 데이터 클러스터링에 자주 사용된다. 자연 언어 처리 분야에는 확률적 문맥 자유 문법(probabilistic context-free grammar)의 자율 유도를 위한 두 가지 중요한 알고리즘의 예로 바움-웰치 알고리즘(Baum-Welch algorithm)과 내부-외부 알고리즘(inside-outside algorithm)이 있다. 심리측정학에서 기댓값 최대화 알고리즘은 문항 반응 이론 모델의 아이템 매개변수와 잠재 능력의 추정을 위해 거의 없어서는 안된다. 기댓값 최대화 알고리즘은 누락된 데이터를 처리하고 미확인 변수를 관찰하는 능력이 있어 포트폴리오 리스크(portfolio risk)의 가격을 정하고 관리하는 유용한 도구가 되고 있다. 기댓값 최대화 알고리즘은 또한 의학 영상 복원, 특히 양전자 방출 단층촬영과 단일광자방출단층활영(single photon emission computed tomography)에 널리 쓰인다.

9. 기댓값 최대화 알고리즘의 필터링과 평활화

칼만 필터는 일반적으로 온라인 상태 추정에 사용되며, 최소 분산 평활기는 오프라인 또는 배치 상태 추정에 사용된다. 그러나 이러한 최소 분산 해법에는 상태 공간 모델 매개변수에 대한 추정치가 필요하다. 기댓값 최대화 알고리즘은 결합 상태 및 매개변수 추정 문제를 해결하는 데 사용할 수 있다.

필터링 및 평활화 기댓값 최대화 알고리즘은 다음의 2단계 절차를 반복함으로써 나타난다.

;E-단계

: 현재 매개변수 추정값으로 설계된 칼만 필터 또는 최소 분산 평활기를 작동하여 업데이트된 상태 추정값을 얻는다.

;M-단계

: 필터링되거나 평활화된 상태 추정값을 최대우도 계산 내에서 사용하여 업데이트된 매개변수 추정값을 얻는다.

칼만 필터 또는 최소 분산 평활기가 덧셈 백색 잡음이 있는 단일 입력 단일 출력 시스템의 측정값에서 작동한다고 가정한다. 업데이트된 측정 노이즈 분산 추정값은 최대우도 계산에서 얻을 수 있다.

: $\widehat{\sigma}^2_v = \frac{1}{N} \sum_{k=1}^N {(z_k-\widehat{x}_k)}^2,$

여기서 $\widehat{x}_k$ 는 N개의 스칼라 측정값 $z_k$ 에서 필터 또는 평활기로 계산된 스칼라 출력 추정값이다. 위의 업데이트는 푸아송 측정 노이즈 강도를 업데이트하는 데에도 적용할 수 있다. 마찬가지로, 1차 자기 회귀 프로세스의 경우, 업데이트된 프로세스 노이즈 분산 추정값은 다음과 같이 계산할 수 있다.

: $\widehat{\sigma}^2_w = \frac{1}{N} \sum_{k=1}^N {(\widehat{x}_{k+1}-\widehat{F}\widehat_k)}^2,$

여기서 $\widehat{x}_k$ 및 $\widehat{x}_{k+1}$ 는 필터 또는 평활기로 계산된 스칼라 상태 추정값이다. 업데이트된 모델 계수 추정값은 다음을 통해 얻는다.

: $\widehat{F} = \frac{\sum_{k=1}^N {(\widehat{x}_{k+1}-\widehat{F} \widehat{x}_k)}^2}{\sum_{k=1}^N \widehat{x}_k^2}.$

위와 같은 매개변수 추정값의 수렴은 잘 연구되었다.^{[en-28]논문 Riccati Equation and EM Algorithm Convergence for Inertial Navigation Alignment 2009-01}^{[en-29]논문 EM Algorithm State Matrix Estimation for Navigation 2010-05}^{[en-30]논문 Iterative Smoother-Based Variance Estimation 2012-05}^{[en-31]논문 Iterative Filtering and Smoothing of Measurements Possessing Poisson Noise 2015-09}

칼만 필터는 일반적으로 온라인 상태 추정에 사용되고 최소 분산 평활화는 오프라인 또는 배치 상태 추정에 사용된다. 그러나 이러한 최소 분산 해법들을 위해서는 상태공간 모델의 매개변수 추정이 필요하다. 기댓값 최대화 알고리즘은 절리 상태와 모수 추정 문제를 푸는데 사용될 수 있다.

기댓값 최대화 알고리즘의 필터링과 평활화는 아래의 두 단계를 반복함으로써 일어난다.

;기댓값 단계(E step)

: 현재 모수 추정으로 설계된 칼만 필터 또는 최소 분산 평활화를 적용하여 갱신된 상태 추정을 얻는다.

;최대화 단계(M step)

: 최대가능도 계산과 필터 또는 평활화 된 상태 추정을 사용해서 갱신된 매개변수 추정을 얻는다.

칼만 필터 또는 최소 분산 평활화가 하나의 입력을 받고 하나의 출력을 하는 시스템에서 잡음 섞인 측정을 한다고 가정하자. 최대가능도 계산으로부터 갱신된 측정 잡음 분산 추정을 얻을 수 있다.

: $\hat{\sigma}^{2}_v = \frac{1}{N} \sum_{k=1}^N {(z_k-\hat{x}_{k})}^{2}$

이 때 $\hat{x}_k$ 는 N 스칼라 측정인 ${z_k}$ 으로부터 필터 또는 평활화에 의해 계산된 스칼라 출력 추정이다. 비슷하게 1차 자기회귀 과정을 위해, 갱신된 과정 잡음 분산 추정이 다음과 같이 계산된다.

: $\hat{\sigma}^{2}_w = \frac{1}{N} \sum_{k=1}^N {(\hat{x}_{k+1}-\hat{F}\hat_{k})}^{2}$

이 때 $\hat{x}_k$ 와 $\hat{x}_{k+1}$ 가 필터 또는 평활화에 의해 계산된 스칼라 상태 추정들이다. 갱신된 모델 계수 추정은 다음을 통해서 얻어진다.

: $\hat{F} = \frac{\sum_{k=1}^N (\hat{x}_{k+1}-\hat{F} \hat{x}_k)}{\sum_{k=1}^N \hat{x}_k^{2}}$ .

위와 같은 모수 추정의 수렴에 대해서 잘 연구되어 있다.^{[ko-13]저널 Riccati Equation and EM Algorithm Convergence for Inertial Navigation Alignment 2009-01}^{[ko-14]저널 EM Algorithm State Matrix Estimation for Navigation 2010-05}^{[ko-15]저널 Iterative Smoother-Based Variance Estimation 2012-05}

10. 변종

켤레 기울기와 수정된 뉴턴 방법(뉴턴-랩슨)을 사용하는 방법과 같이 EM 알고리즘의 느린 수렴을 가속화하기 위한 여러 방법이 제안되었다.^{[en-32]논문 Acceleration of the EM Algorithm by using Quasi-Newton Methods}^{[ko-16]저널 Acceleration of the EM Algorithm by using Quasi-Newton Methods} 또한 EM은 제약된 추정 방법과 함께 사용할 수 있다.

''매개변수 확장 기대 최대화(PX-EM)'' 알고리즘은 "귀속된 완전 데이터에서 캡처된 추가 정보를 활용하여 M 단계 분석을 수정하기 위한 '공분산 조정'을 사용"하여 속도를 향상시킨다.^{[en-33]논문 Parameter expansion to accelerate EM: The PX-EM algorithm}

''기대 조건부 최대화(ECM)''는 각 M 단계를 각 매개변수 ''θ''_''i''가 다른 매개변수가 고정된 상태에서 조건부로 개별적으로 최대화되는 일련의 조건부 최대화(CM) 단계로 대체한다.^{[en-34]논문 Maximum likelihood estimation via the ECM algorithm: A general framework}^{[ko-17]저널 Maximum likelihood estimation via the ECM algorithm: A general framework} 자체적으로 ''기대 조건부 최대화 중 하나(ECME)'' 알고리즘으로 확장할 수 있다.^{[en-35]논문 The ECME Algorithm: A Simple Extension of EM and ECM with Faster Monotone Convergence}

이 아이디어는 최대화-최대화 절차 섹션에 설명된 대로 E 단계와 M 단계 모두에 대해 목적 함수 ''F''의 증가만 추구하는 ''일반화된 기대 최대화(GEM)'' 알고리즘에서 더욱 확장되었다.^{[en-21]서적 Learning in Graphical Models MIT Press 2009-03-22}^{[ko-11]저널 A view of the EM algorithm that justifies incremental, sparse, and other variants MIT Press 2009-03-22} GEM은 분산 환경에서 더욱 개발되었으며 유망한 결과를 보여준다.^{[en-36]간행물 Accelerating Expectation–Maximization Algorithms with Frequent Updates}

또한 EM 알고리즘을 '''MM''' (맥락에 따라 Majorize/Minimize 또는 Minorize/Maximize) 알고리즘의 하위 클래스로 간주하고,^{[en-37]논문 A Tutorial on MM Algorithms 2004}^{[ko-18]저널 A Tutorial on MM Algorithms 2011-07-20} 따라서 보다 일반적인 경우에서 개발된 모든 메커니즘을 사용할 수 있다.

10. 1. α-EM 알고리즘

EM 알고리즘에서 사용되는 Q 함수는 로그 우도에 기반하므로 로그-EM 알고리즘으로 간주된다. 로그 우도의 사용은 α-로그 우도 비율의 사용으로 일반화될 수 있다. 관측된 데이터의 α-로그 우도 비율은 α-로그 우도 비율의 Q 함수와 α-발산을 사용하여 정확히 등식으로 표현할 수 있다. 이 Q 함수를 구하는 것이 일반화된 E 단계이며, 이것의 최대화가 일반화된 M 단계이다. 이 쌍을 α-EM 알고리즘이라고 하며^{[en-38]논문 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures} 로그-EM 알고리즘을 하위 클래스로 포함한다. 마쓰야마 야스오(Yasuo Matsuyama)의 α-EM 알고리즘은 로그-EM 알고리즘의 정확한 일반화이다. 기울기 또는 헤세 행렬의 계산은 필요하지 않다. α-EM은 적절한 α를 선택하여 로그-EM 알고리즘보다 빠른 수렴을 보여준다. α-EM 알고리즘은 은닉 마르코프 모델 추정 알고리즘 α-HMM의 더 빠른 버전으로 이어진다.^{[en-39]논문 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs}

EM 알고리즘은 관측 데이터의 로그 우도를, E 단계와 M 단계의 반복을 통해 최대화하는 알고리즘이므로, 정확히는 log-EM 알고리즘이라고 해야 한다. 로그 함수에는 α-log라고 불리는 일반화된 로그가 있으므로, 이를 사용하면 log-EM을 특례로 포함하는 알고리즘을 만들 수 있다. 다만, 이 경우에는 우도가 아닌 α-log 우도비와 α 다이버전스를 사용하여 기본 등식을 도출하게 된다. 이렇게 해서 얻어진 것이 α-EM 알고리즘^{[ja-3]논문 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures}이며, log-EM 알고리즘을 서브클래스로 포함하고 있다. α-EM 알고리즘은 적절한 α를 선택함으로써 log-EM 알고리즘보다 더 빨라진다. 또한, log-EM이 은닉 마르코프 모델 추정 알고리즘(Baum-Welch 알고리즘)을 포함하는 것처럼, α-EM 알고리즘에서 고속의 α-HMM 알고리즘을 얻을 수 있다.^{[ja-4]논문 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs}

기댓값 최대화 알고리즘에 사용되는 Q-함수는 로그가능도를 기반으로 한다. 그러므로 log-EM 알고리즘으로 간주된다. 로그가능도의 사용은 α-로그가능도 비율로 일반화될 수 있다. 그러면, 관찰된 데이터의 α-로그가능도 비율은 그것의 Q-함수와 α-발산을 사용한 등식으로 정확하게 표현된다. 이 Q-함수를 얻는 것은 일반화된 E 단계이다. 그것의 최대화는 일반화된 M 단계이다. 이 두 단계를 α-EM 알고리즘^{[ko-19]저널 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures}이라고 부르며 log-EM 알고리즘이 이에 하위 분류로 포함된다. 따라서, 야스오 마쓰야마/Yasuo Matsuyama^영어의 α-EM 알고리즘은 정확히 log-EM 알고리즘의 일반화이다. 기울기 또는 Hessian 행렬의 계산이 필요 없다. α-EM은 알맞은 α를 선택함으로써 log-EM 알고리즘보다 더 빠르게 수렴한다. α-EM 알고리즘은 은닉 마르코프 모델 추정 알고리즘 α-HMM^{[ko-20]저널 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs}의 더 빠른 버전으로 이어진다.

11. 변분 베이즈 근사법과의 관계

EM 알고리즘은 부분적으로 비베이즈적인 최대 우도 방법이다. 최종 결과는 ''θ''에 대한 점 추정치(최대 우도 추정치 또는 사후 모드)와 함께 잠재 변수에 대한 확률 분포(베이즈 스타일)를 제공한다. ''θ''와 잠재 변수에 대한 확률 분포를 제공하는 완전한 베이즈 버전이 필요할 수 있다. 추론에 대한 베이즈 접근 방식은 단순히 ''θ''를 또 다른 잠재 변수로 취급하는 것이다. 이러한 패러다임에서는 E 단계와 M 단계의 구분이 사라진다. 위에서 설명한 것처럼 인수분해된 Q 근사(변분 베이즈)를 사용하는 경우, 각 잠재 변수(이제 ''θ'' 포함)에 대해 반복하여 한 번에 하나씩 최적화할 수 있다. 이제 반복당 ''k'' 단계가 필요하며, 여기서 ''k''는 잠재 변수의 수이다. 그래프 모델의 경우 각 변수의 새로운 ''Q''는 해당 변수의 마르코프 블랭킷에만 의존하므로 효율적인 추론을 위해 지역적 메시지 전달을 사용할 수 있기 때문에 쉽게 수행할 수 있다.

기댓값 최대화 알고리즘은 부분적으로 베이즈가 아닌 최대가능도방법이다. 최종 결과는 (베이즈 방식의) 잠재변수와 ''θ'' (최대가능도 또는 사후 최빈값)의 점추정에 대한 확률분포로 나타난다. 잠재변수처럼 ''θ''에 대한 확률분포로 나타나는 완전한 베이즈 방식의 버전을 생각해 볼 수 있다. 추론을 위한 베이즈 방식의 접근법은 간단하게 ''θ''을 다른 잠재변수와 같이 취급한다. 이 패러다임에선 E 단계와 M 단계의 구분이 없어진다. 만약 위에서 말한 변분 베이즈 근사법과 같이 인수분해된 Q 근사값을 사용하면, 각각의 잠재변수(''θ''가 포함된)에 대해서 반복하고 한 번에 하나씩 최적화할 수 있다. 그러면 ''k''가 잠재변수의 개수라고 할 때, 한 번 반복할 때마다 ''k'' 단계들이 있다. 그래프 모델에서 앞의 방법은 각각의 변수의 새로운 ''Q''를 마르코프 블랭킷에만 의존시킴으로써 쉽게 만들 수 있어서, 국소 메시지 전달이 효율적인 추론으로 사용될 수 있다.

12. 기하학적 해석

정보 기하학에서 E 단계와 M 단계는 e-연결과 m-연결이라고 불리는 이중 아핀 접속 하의 투영으로 해석된다. 쿨백-라이블러 발산 또한 이러한 관점에서 이해할 수 있다.

쿨백-라이블러 발산( $\mathrm{KL}(q||p_{X,\theta})$ )이 최솟값 0이 되는 경우는 $q=p_{\theta,X}$ 인 경우뿐이므로, $\mathcal{L}(q,\theta)$ 는

: $q(Z)=p(Z|X,\theta)$

가 충족되는 경우에 최댓값을 갖는다. 즉, EM 알고리즘에서의 E단계는 $\theta=\hat{\theta}^{(t)}$ 를 고정한 상태에서 $\mathcal{L}(q,\theta)$ 를 최대화하는 $q$ 인

: $\hat{q}^{(t)} := p_{X,\hat{\theta}^{(t)}} = \underset{q}{\operatorname{arg\,max}}\mathcal{L}(q,\hat{\theta}^{(t)})$

를 구하는 단계이다.

정보 기하학정보 기하학/information geometry^영어에서, E 단계와 M 단계는 이중 아핀 접속의 사영투영/projection^영어으로 해석되고, e-연결e-연결/e-connection^영어과 m-연결m-연결/m-connection^영어로 불린다. 쿨백-라이블러 발산 또한 이 용어들을 사용해서 해석될 수 있다.

13. 예제

$\mathbf{x} = (\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n)$ 을 $d$ 차원의 두 다변량 정규 분포의 혼합 모델로부터 얻은 $n$ 개의 독립적인 관측값의 표본이라고 하고, $\mathbf{z} = (z_1,z_2,\ldots,z_n)$ 를 관측값이 유래된 성분을 결정하는 잠재 변수라고 하자.^{[en-22]서적 The Elements of Statistical Learning Springer}

: $X_i \mid(Z_i = 1) \sim \mathcal{N}_d(\boldsymbol{\mu}_1,\Sigma_1)$ 이고 $X_i \mid(Z_i = 2) \sim \mathcal{N}_d(\boldsymbol{\mu}_2,\Sigma_2),$

여기서

: $\operatorname{P} (Z_i = 1 ) = \tau_1 \,$ 이고 $\operatorname{P} (Z_i=2) = \tau_2 = 1-\tau_1.$

목표는 각 가우시안 간의 ''혼합'' 값과 각 가우시안의 평균 및 공분산을 나타내는 미지의 매개변수를 추정하는 것이다.

: $\theta = \big( \boldsymbol{\tau},\boldsymbol{\mu}_1,\boldsymbol{\mu}_2,\Sigma_1,\Sigma_2 \big),$

여기서 불완전 데이터 우도 함수는 다음과 같다.

: $L(\theta;\mathbf{x}) = \prod_{i=1}^n \sum_{j=1}^2 \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j),$

완전 데이터 우도 함수는 다음과 같다.

: $L(\theta;\mathbf{x},\mathbf{z}) = p(\mathbf{x},\mathbf{z} \mid \theta) = \prod_{i=1}^n \prod_{j=1}^2 \ [f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j) \tau_j] ^{\mathbb{I}(z_i=j)},$

또는

: $L(\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\},$

여기서 $\mathbb{I}$ 는 지시 함수이고 $f$ 는 다변량 정규 분포의 확률 밀도 함수이다.

마지막 등식에서 각 에 대해 지시 함수 $\mathbb{I}(z_i=j)$ 중 하나는 0이고, 다른 지시 함수는 1이다. 따라서 내부 합은 하나의 항으로 줄어든다.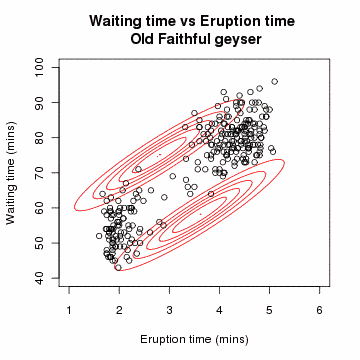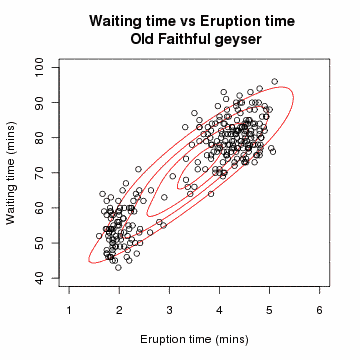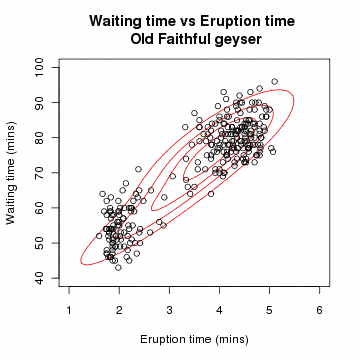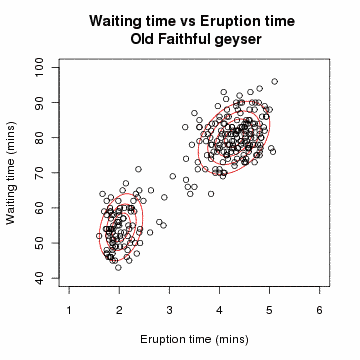

올드페이스풀 간헐천 데이터에 가우시안 혼합 모델에 맞추는 EM 알고리즘을 보여주는 애니메이션. 알고리즘은 난수로 만들어진 초기값부터 시작해서 수렴해 가는 과정을 보여준다.

두 개의

d

차원 다변량 정규분포가 혼합되어 있는 경우, 보통 이 모델에서

d

차원 값을 수집하는 것은 가능하지만 그 값이 두 분포 중 어느 분포에서 나온 것인지는 알 수 없는 경우가 많다. 이 문단에서는 이러한 경우에 대한 기댓값 최대화 알고리즘을 유도한다.

전체

n

개의 점을 수집하였을 때,

i

번째 수집되는 값은

(x_i, z_i)

로 나타낼 수 있다. 여기에서

x_i

는

d

차원 점을 가리키는 관측 가능한 변수, 그리고

z_i

는 두 개의 정규분포 중 어느 분포에서 수집되었는지를 가리키는 관측 불가능한 변수이다.

i

번째 값이 두 분포 중 어느 분포에서 수집되는지에 대한 확률은

i

와 독립적이기 때문에,

P(z_i)

는

i

에 관계없는 매개변수로 표현할 수 있다. 이 값을

P(z_i=1) = \tau_1, P(z_i=2) = \tau_2

인 벡터

\boldsymbol\tau = (\tau_1, \tau_2)

로 표기하도록 한다(

\tau_1 + \tau_2 = 1

).

마지막으로, 두 다변량 정규분포를 각각

\mathcal{N}_d(\boldsymbol\mu_1, \Sigma_1)

,

\mathcal{N}_d(\boldsymbol\mu_2, \Sigma_2)

로 표기하기로 한다.

즉,

:

X_i |(Z_i = 1) \sim \mathcal{N}_d(\boldsymbol{\mu}_1,\Sigma_1)

이고

X_i |(Z_i = 2) \sim \mathcal{N}_d(\boldsymbol{\mu}_2,\Sigma_2)

이다.

그렇다면 이 모델에서 매개변수는

\boldsymbol{\theta} = (\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \Sigma_1, \Sigma_2, \boldsymbol\tau)

가 된다.

이제 가능도 함수

L(\boldsymbol\theta;\mathbf{x},\mathbf{z})

를 다음과 같이 표현할 수 있다:

불완전한 데이터 가능도 함수는

:

L(\theta;\mathbf{x},\mathbf{z}) = P(\mathbf{x},\mathbf{z}| \theta) = \prod_{i=1}^n \sum_{j=1}^2 \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j)

이고,

완전한 데이터 가능도 함수는

:

L(\boldsymbol\theta;\mathbf{x},\mathbf{z}) = P(\mathbf{x},\mathbf{z} \vert \boldsymbol\theta) = \prod_{i=1}^n  \sum_{j=1}^2  \mathbb{I}(z_i=j) \ \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j)

이다.

여기에서

\mathbb{I}

는 지시 함수이고,

f

는 다변량 정규분포의 확률 밀도 함수이다. 여기에서

f

를 풀어서 쓰면 다음과 같이 정리된다.

:

L(\boldsymbol\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{n}{2} \log(2\pi) \big] \right\}

13. 1. 예제 1: 정규분포 혼합 모델

k-평균과 EM을 ELKI로 시각화한 인공 데이터에 대한 비교. 분산을 사용하여 EM 알고리즘은 정규 분포를 정확하게 설명할 수 있는 반면, k-평균은 데이터를 보로노이 셀로 분할한다. 군집 중심은 더 밝고 큰 기호로 표시된다.

\mathbf{x} = (\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_n)

을

d

차원의 두 다변량 정규 분포의 혼합 모델로부터 얻은

n

개의 독립적인 관측값의 표본이라고 하고,

\mathbf{z} = (z_1,z_2,\ldots,z_n)

를 관측값이 유래된 성분을 결정하는 잠재 변수라고 하자.^{[en-22]서적 The Elements of Statistical Learning Springer}

:

X_i \mid(Z_i = 1) \sim \mathcal{N}_d(\boldsymbol{\mu}_1,\Sigma_1)

이고

X_i \mid(Z_i = 2) \sim \mathcal{N}_d(\boldsymbol{\mu}_2,\Sigma_2),

여기서

:

\operatorname{P} (Z_i = 1 ) = \tau_1 \,

이고

\operatorname{P} (Z_i=2) = \tau_2 = 1-\tau_1.

목표는 각 가우시안 간의 ''혼합'' 값과 각 가우시안의 평균 및 공분산을 나타내는 미지의 매개변수를 추정하는 것이다.

:

\theta = \big( \boldsymbol{\tau},\boldsymbol{\mu}_1,\boldsymbol{\mu}_2,\Sigma_1,\Sigma_2 \big),

여기서 불완전 데이터 우도 함수는 다음과 같다.

:

L(\theta;\mathbf{x}) = \prod_{i=1}^n \sum_{j=1}^2 \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j),

완전 데이터 우도 함수는 다음과 같다.

:

L(\theta;\mathbf{x},\mathbf{z}) = p(\mathbf{x},\mathbf{z} \mid \theta) = \prod_{i=1}^n  \prod_{j=1}^2  \ [f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j) \tau_j] ^{\mathbb{I}(z_i=j)},

또는

:

L(\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\},

여기서

\mathbb{I}

는 지시 함수이고

f

는 다변량 정규 분포의 확률 밀도 함수이다.

마지막 등식에서 각 에 대해 지시 함수

\mathbb{I}(z_i=j)

중 하나는 0이고, 다른 지시 함수는 1이다. 따라서 내부 합은 하나의 항으로 줄어든다.

두 개의

d

차원 다변량 정규분포가 혼합되어 있는 경우, 보통 이 모델에서

d

차원 값을 수집하는 것은 가능하지만 그 값이 두 분포 중 어느 분포에서 나온 것인지는 알 수 없는 경우가 많다. 이 문단에서는 이러한 경우에 대한 기댓값 최대화 알고리즘을 유도한다.

전체

n

개의 점을 수집하였을 때,

i

번째 수집되는 값은

(x_i, z_i)

로 나타낼 수 있다. 여기에서

x_i

는

d

차원 점을 가리키는 관측 가능한 변수, 그리고

z_i

는 두 개의 정규분포 중 어느 분포에서 수집되었는지를 가리키는 관측 불가능한 변수이다.

i

번째 값이 두 분포 중 어느 분포에서 수집되는지에 대한 확률은

i

와 독립적이기 때문에,

P(z_i)

는

i

에 관계없는 매개변수로 표현할 수 있다. 이 값을

P(z_i=1) = \tau_1, P(z_i=2) = \tau_2

인 벡터

\boldsymbol\tau = (\tau_1, \tau_2)

로 표기하도록 한다(

\tau_1 + \tau_2 = 1

).

마지막으로, 두 다변량 정규분포를 각각

\mathcal{N}_d(\boldsymbol\mu_1, \Sigma_1)

,

\mathcal{N}_d(\boldsymbol\mu_2, \Sigma_2)

로 표기하기로 한다.

즉,

:

X_i |(Z_i = 1) \sim \mathcal{N}_d(\boldsymbol{\mu}_1,\Sigma_1)

이고

X_i |(Z_i = 2) \sim \mathcal{N}_d(\boldsymbol{\mu}_2,\Sigma_2)

이다.

그렇다면 이 모델에서 매개변수는

\boldsymbol{\theta} = (\boldsymbol{\mu}_1, \boldsymbol{\mu}_2, \Sigma_1, \Sigma_2, \boldsymbol\tau)

가 된다.

이제 가능도 함수

L(\boldsymbol\theta;\mathbf{x},\mathbf{z})

를 다음과 같이 표현할 수 있다:

불완전한 데이터 가능도 함수는

:

L(\theta;\mathbf{x},\mathbf{z}) = P(\mathbf{x},\mathbf{z}| \theta) = \prod_{i=1}^n \sum_{j=1}^2 \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j)

이고,

완전한 데이터 가능도 함수는

:

L(\boldsymbol\theta;\mathbf{x},\mathbf{z}) = P(\mathbf{x},\mathbf{z} \vert \boldsymbol\theta) = \prod_{i=1}^n  \sum_{j=1}^2  \mathbb{I}(z_i=j) \ \tau_j \ f(\mathbf{x}_i;\boldsymbol{\mu}_j,\Sigma_j)

이다.

여기에서

\mathbb{I}

는 지시 함수이고,

f

는 다변량 정규분포의 확률 밀도 함수이다. 여기에서

f

를 풀어서 쓰면 다음과 같이 정리된다.

:

L(\boldsymbol\theta;\mathbf{x},\mathbf{z}) = \exp \left\{ \sum_{i=1}^n \sum_{j=1}^2 \mathbb{I}(z_i=j) \big[ \log \tau_j -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big] \right\}

13. 1. 1. 기댓값 단계(E step)

현재의 매개변수 추정값 ''θ''^(''t'')가 주어지면, ''Z''_''i''의 조건부 분포는 베이즈 정리에 의해 ''τ''로 가중된 정규 확률 밀도 함수의 비례 높이로 결정된다.

:

T_{j,i}^{(t)} := \operatorname{P}(Z_i=j \mid X_i=\mathbf{x}_i ;\theta^{(t)}) = \frac{\tau_j^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_j^{(t)},\Sigma_j^{(t)})}{\tau_1^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_1^{(t)},\Sigma_1^{(t)}) + \tau_2^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_2^{(t)},\Sigma_2^{(t)})}.

이것들을 "멤버십 확률"이라고 하며, 일반적으로 E 단계의 결과로 간주된다.

이 E 단계는 Q에 대한 이 함수를 설정하는 것에 해당한다.

:

\begin{align}Q(\theta\mid\theta^{(t)})&= \operatorname{E}_{\mathbf{Z}\mid\mathbf{X}=\mathbf{x};\mathbf{\theta}^{(t)}} [\log L(\theta;\mathbf{x},\mathbf{Z}) ] \\&= \operatorname{E}_{\mathbf{Z}\mid\mathbf{X}=\mathbf{x};\mathbf{\theta}^{(t)}} [\log \prod_{i=1}^{n}L(\theta;\mathbf{x}_i,Z_i) ] \\&= \operatorname{E}_{\mathbf{Z}\mid\mathbf{X}=\mathbf{x};\mathbf{\theta}^{(t)}} [\sum_{i=1}^n \log L(\theta;\mathbf{x}_i,Z_i) ] \\&= \sum_{i=1}^n\operatorname{E}_{Z_i\mid X_i=x_i;\mathbf{\theta}^{(t)}} [\log L(\theta;\mathbf{x}_i,Z_i) ] \\&= \sum_{i=1}^n \sum_{j=1}^2 P(Z_i =j \mid X_i = \mathbf{x}_i; \theta^{(t)}) \log L(\theta_j;\mathbf{x}_i,j) \\&= \sum_{i=1}^n \sum_{j=1}^2 T_{j,i}^{(t)} \big[ \log \tau_j  -\tfrac{1}{2} \log |\Sigma_j| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{d}{2} \log(2\pi) \big].\end{align}

합계 내부의

\log L(\theta;\mathbf{x}_i,Z_i)

의 기대값은 훈련 세트의 각

\mathbf{x}_i

에 대해 다를 수 있는 확률 밀도 함수

P(Z_i \mid X_i = \mathbf{x}_i; \theta^{(t)})

에 대해 취해진다. E 단계의 모든 것은 E 단계 섹션의 시작 부분에 있는 방정식에 따라 계산되는

T_{j,i}

를 제외하고 단계가 수행되기 전에 알려져 있다.

''τ''와 '''μ'''/'''Σ'''가 별도의 선형 항에 나타나므로 이 전체 조건부 기댓값을 한 단계로 계산할 필요가 없으며, 따라서 독립적으로 최대화할 수 있다.

모수

\boldsymbol\theta^{(t)}

에 대하여

z_i

에 대한 확률분포

\operatorname{P}(Z_i=j | X_i=\mathbf{x}_i ;\boldsymbol\theta^{(t)})

는 다음과 같이 계산한다.

:

T_{j,i}^{(t)} := \operatorname{P}(Z_i=j | X_i=\mathbf{x}_i ;\boldsymbol\theta^{(t)}) = \frac{\tau_j^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_j^{(t)},\Sigma_j^{(t)})}{\tau_1^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_1^{(t)},\Sigma_1^{(t)}) + \tau_2^{(t)} \ f(\mathbf{x}_i;\boldsymbol{\mu}_2^{(t)},\Sigma_2^{(t)})}

그러면 기댓값 단계의

Q

함수는 다음과 같이 계산된다.

:

\begin{align}Q(\boldsymbol\theta|\boldsymbol\theta^{(t)})&= \operatorname{E} [\log L(\boldsymbol\theta;\mathbf{x},\mathbf{Z}) ] \\&= \operatorname{E} [\log \prod_{i=1}^{n}L(\boldsymbol\theta;\mathbf{x}_i,\mathbf{z}_i) ] \\&= \operatorname{E} [\sum_{i=1}^n \log L(\boldsymbol\theta;\mathbf{x}_i,\mathbf{z}_i) ] \\&= \sum_{i=1}^n\operatorname{E} [\log L(\boldsymbol\theta;\mathbf{x}_i,\mathbf{z}_i) ] \\&= \sum_{i=1}^n \sum_{j=1}^2 T_{j,i}^{(t)} \big[ \log \tau_j  -\tfrac{1}{2} \log \Sigma_j -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_j)^\top\Sigma_j^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_j) -\tfrac{1}{2} \log(2\pi) \big]\end{align}

13. 1. 2. 최대화 단계(M step)

Q(\theta \mid \theta^{(t)} )

가 이차 형식이라는 것은

\theta

의 최대화 값을 결정하는 것이 비교적 간단하다는 것을 의미한다. 또한,

\tau

,

(\boldsymbol{\mu}_1,\Sigma_1)

및

(\boldsymbol{\mu}_2,\Sigma_2)

는 모두 별도의 선형 항에 나타나므로 독립적으로 최대화될 수 있다.

먼저, 제약 조건

\tau_1+\tau_2=1

을 갖는

\tau

를 고려하면,

:

\begin{align}\boldsymbol{\tau}^{(t+1)}&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}}\  Q(\theta \mid \theta^{(t)} ) \\&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}} \ \left\{ \left[  \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 + \left[  \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2  \right\}.\end{align}

이것은 이항 분포의 최대우도 추정치와 같은 형식을 가지므로

:

\tau^{(t+1)}_j = \frac{\sum_{i=1}^n T_{j,i}^{(t)}}{\sum_{i=1}^n (T_{1,i}^{(t)} + T_{2,i}^{(t)} ) } = \frac{1}{n} \sum_{i=1}^n T_{j,i}^{(t)}.

(\boldsymbol{\mu}_1,\Sigma_1)

의 다음 추정치는 다음과 같다.

:

\begin{align}(\boldsymbol{\mu}_1^{(t+1)},\Sigma_1^{(t+1)})&= \underset{\boldsymbol{\mu}_1,\Sigma_1} \operatorname{arg\,max}\ Q(\theta \mid \theta^{(t)} ) \\&= \underset{\boldsymbol{\mu}_1,\Sigma_1} \operatorname{arg\,max}\ \sum_{i=1}^n T_{1,i}^{(t)} \left\{ -\tfrac{1}{2} \log |\Sigma_1| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_1)^\top\Sigma_1^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_1) \right\}\end{align}.

이것은 정규 분포에 대한 가중 최대 우도 추정치와 같은 형식을 가지므로

:

\boldsymbol{\mu}_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} \mathbf{x}_i}{\sum_{i=1}^n T_{1,i}^{(t)}}

및

\Sigma_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)}) (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)})^\top }{\sum_{i=1}^n T_{1,i}^{(t)}}

그리고 대칭에 의해

:

\boldsymbol{\mu}_2^{(t+1)} = \frac{\sum_{i=1}^n T_{2,i}^{(t)} \mathbf{x}_i}{\sum_{i=1}^n T_{2,i}^{(t)}}

및

\Sigma_2^{(t+1)} = \frac{\sum_{i=1}^n T_{2,i}^{(t)} (\mathbf{x}_i - \boldsymbol{\mu}_2^{(t+1)}) (\mathbf{x}_i - \boldsymbol{\mu}_2^{(t+1)})^\top }{\sum_{i=1}^n T_{2,i}^{(t)}}.

이제 최대화 단계를 계산한다.

Q

함수는

\tau_j

에 대한 식과

(\boldsymbol{\mu}_j,\Sigma_j)

에 대한 식의 선형 결합이기 때문에,

\tau_j

와

(\boldsymbol{\mu}_j,\Sigma_j)

에 대해 독립적으로 최대화를 계산하는 것이 가능하다.

먼저 모수

\boldsymbol{\tau}^{(t+1)}

는 다음과 같이 유도된다.

:

\begin{align}\boldsymbol{\tau}^{(t+1)}&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}}\  Q(\theta | \theta^{(t)} ) \\&= \underset{\boldsymbol{\tau}} {\operatorname{arg\,max}} \ \left\{ \left[  \sum_{i=1}^n T_{1,i}^{(t)} \right] \log \tau_1 + \left[  \sum_{i=1}^n T_{2,i}^{(t)} \right] \log \tau_2  \right\}\end{align}

이 식은 이항분포에서의 최대가능도를 계산하는 경우와 동일하며, 따라서 다음과 같이 계산할 수 있다.

:

\tau^{(t+1)}_j = \frac{\sum_{i=1}^n T_{j,i}^{(t)}}{\sum_{i=1}^n (T_{1,i}^{(t)} + T_{2,i}^{(t)} ) } = \frac{1}{n} \sum_{i=1}^n T_{j,i}^{(t)}

다음으로

(\boldsymbol{\mu}_1^{(t+1)}, \Sigma_1^{(t+1)})

에 대한 식은 다음과 같다.

:

\begin{align}(\boldsymbol{\mu}_1^{(t+1)},\Sigma_1^{(t+1)})&= \underset{\boldsymbol{\mu}_1,\Sigma_1} {\operatorname{arg\,max}}\  Q(\theta | \theta^{(t)} ) \\&= \underset{\boldsymbol{\mu}_1,\Sigma_1} {\operatorname{arg\,max}}\  \sum_{i=1}^n T_{1,i}^{(t)} \left\{ -\tfrac{1}{2} \log |\Sigma_1| -\tfrac{1}{2}(\mathbf{x}_i-\boldsymbol{\mu}_1)^\top\Sigma_1^{-1} (\mathbf{x}_i-\boldsymbol{\mu}_1) \right\}\end{align}

이 식은 다변량 정규분포에서의 최대가능도를 계산하는 식과 유사하며, 다음과 같이 계산할 수 있다.

:

\boldsymbol{\mu}_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} \mathbf{x}_i}{\sum_{i=1}^n T_{1,i}^{(t)}}

:

\Sigma_1^{(t+1)} = \frac{\sum_{i=1}^n T_{1,i}^{(t)} (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)}) (\mathbf{x}_i - \boldsymbol{\mu}_1^{(t+1)})^\top }{\sum_{i=1}^n T_{1,i}^{(t)}}

(\boldsymbol{\mu}_2^{(t+1)}, \Sigma_2^{(t+1)})

도 같은 방식으로 구할 수 있다.

13. 1. 3. 알고리즘의 종료

만약 미리 설정된 임계값 이하의

\varepsilon

에 대해

E_{Z\mid\theta^{(t)},\mathbf{x}}[\log L(\theta^{(t)};\mathbf{x},\mathbf{Z})] \leq E_{Z\mid\theta^{(t-1)},\mathbf{x}}[\log L(\theta^{(t-1)};\mathbf{x},\mathbf{Z})] + \varepsilon

이면 반복 과정을 종료한다. 반복 과정은 각 과정에서 가능도 사이의 증가폭이 사전에 정의된 기준점 아래로 내려오면 종료한다. 즉, 사전에 정의된 기준점

\epsilon

에 대해서,

\log L(\theta^{t};\mathbf{x},\mathbf{Z}) \leq \log L(\theta^{(t-1)};\mathbf{x},\mathbf{Z}) + \epsilon

이면 종료한다.

13. 1. 4. 일반화

위에 설명된 알고리즘은 둘 이상의 다변량 정규 분포의 혼합에 대해 일반화될 수 있다.

13. 2. 예제 2: 베르누이 혼합 모델

동일한 크기의 이미지

N

개가 주어졌을 때, 이를

\mathbf{x_n} = (x_{n,1}, ..., x_{n,D})^T, n \in \{1, ..., N \}

라 하자. 각 이미지는

D

개의 픽셀로 이루어져 있고 각 픽셀은

0

혹은

1

의 값을 가진다. 즉,

x_{n,i} \in \{ 0, 1 \}

이다. 또한 각각의 픽셀이 서로에 대해 조건부 독립적이라 가정하면, 성분

k

의 모든 이미지에 관한 픽셀

i

의 확률분포는 모수

0 \leq \mu_{k, i} \leq 1

를 갖는 베르누이 분포로 모델링 할 수 있다.

혼합 모델이

K

개의 군집(cluster)을 가진다고 가정할 때, 어떤 이미지가 군집

i

에 속해 있을 확률을

\mathbf{\pi_i}, i \in \{1, ..., K\}, \sum_{i = 1}^K \pi_i = 1

이라 하자.

\mathbf{\pi_i}

는 혼합 계수(mixing coefficient)라 불린다.

이 모델은 어떤 이미지가 특정 군집에 속할 확률변수와 그 군집에서의 픽셀 분포 변수를 모수로 갖는다. 즉,

\theta = (\mathbf{\mu}, \mathbf{\pi})

이고,

\mathbf{\mu} := (\mathbf{\mu_1} \; \mathbf{\mu_2} \;... \;\mathbf{\mu_K} ) = \left( \begin{array}{cccc} \mu_{1, 1} & \mu_{2, 1} & ... & \mu_{K, 1} \\ \mu_{1, 2} & \mu_{2, 2} & ... & \mu_{K, 2} \\ \vdots & \vdots & \ddots & \vdots \\ \mu_{1, D} & \mu_{2, D} & ... & \mu_{K, D} \\ \end{array} \right), \mathbf{\pi} := ( \pi_1, ..., \pi_K )^T

이다.

하나의 트레이닝 이미지(training image)

\mathbf{x}

에 관한 가능도 함수는 다음과 같다.

\begin{align}\,\text{Pr}(\mathbf{x} | \theta) = \,\text{Pr}(\mathbf{x} | \mathbf{\mu}, \mathbf{\pi}) = \sum_{k = 1}^K \pi_k \,\text{Pr}(\mathbf{x}|\mathbf{\mu_k})\end{align}

이 때

\mathbf{x}

가 군집

k

에 의해 생성되었을 확률은 다음과 같다.

\begin{align}\,\text{Pr}(\mathbf{x}|\mathbf{\mu_k}) = \prod_{i = 1}^D \mu_{k, i}^{x_i} (1 - \mu_{k, i})^{1 - x_i}.\end{align}

K

-차원 잠재변수

\mathbf{z_i}, i \in \{1, ..., N \}

을 정의함으로써 주어진 이미지가 어떤 군집에 속할 확률을 모델링 할 수 있다.

\mathbf{z_i}

가

1

-of-

K

표기법으로 나타내어졌다고 하자. 즉,

\mathbf{z_i} := (z_{i, 1}, ..., z_{i, K})^T

에 대하여,

z_{i, j} \in \{0, 1\}, i \in \{ 1, ..., N \}, j \in \{ 1, ..., K \}

이고,

\sum_{j = 1}^{K} z_{i, j} = 1

가 성립한다.

\mathbf{z_i}

의 분포가

\,\text{Pr}(z_{i, j} = 1) = \pi_j

로 주어져 있다고 가정하자. 그러면 다음이 성립한다.

\begin{align}\,\text{Pr}(\mathbf{z_n} | \mathbf{\pi}) = \prod_{i = 1}^K \pi_i^{z_{n, i}}.\end{align}

또한,

\,\text{Pr}(\mathbf{x_n} | z_{n, k} = 1) = \,\text{Pr}(\mathbf{x_n} | \mathbf{\mu_k})

라 하면,

\begin{align}\,\text{Pr}(\mathbf{x_n} | \mathbf{z_n}, \mathbf{\mu}, \mathbf{\pi}) = \prod_{k = 1}^K \,\text{Pr}(\mathbf{x_n} | \mathbf{\mu_k})^{z_{n, k}}.\end{align}

이다.

잠재변수

\mathbf{z_i}

들을 포함하는 집합

\mathbf{Z} := \{ \mathbf{z_1}, ..., \mathbf{z_N} \}

를 정의하고 위 수식을 사용하면,

\begin{align}\,\text{Pr}(\mathbf{Z}|\mathbf{\pi}) = \prod_{n = 1}^N \,\text{Pr}(\mathbf{z_n}|\mathbf{\pi}) = \prod_{n = 1}^N \prod_{k = 1}^K \pi_k^{z_{n, k}}.\end{align}

이 성립하고,

트레이닝 이미지의 집합

\mathbf{X} := \{ \mathbf{x_1}, ..., \mathbf{x_N} \}

를 정의하면

\mathbf{Z}

에 관한

\mathbf{X}

의 조건부 확률분포를 다음과 같이 유도할 수 있다.

\begin{align}\,\text{Pr}(\mathbf{X}|\mathbf{Z}, \mathbf{\mu}, \mathbf{\pi}) = \prod_{n = 1}^N \,\text{Pr}(\mathbf{x_n}|\mathbf{z_n},\mathbf{\mu},\mathbf{\pi}) = \prod_{n = 1}^N \prod_{k = 1}^K \,\text{Pr}(\mathbf{x_n} | \mathbf{\mu_k})^{z_{n, k}} = \prod_{n = 1}^N \prod_{k = 1}^K \left( \prod_{i = 1}^D \mu_{k, i}^{x_{n, i}} (1 - \mu_{k, i})^{1 - x_{n, i}} \right)^{z_{n, k}}.\end{align}

이제 위 수식들과 확률의 곱셈법칙을 이용하면 완전한 데이터 가능도(complete data likelihood^영어)를 구할 수 있고,

\begin{align}\,\text{Pr}(\mathbf{X}, \mathbf{Z}| \mathbf{\mu}, \mathbf{\pi}) = \,\text{Pr}(\mathbf{X} | \mathbf{Z}, \mathbf{\mu}, \mathbf{\pi}) \,\text{Pr}(\mathbf{Z}| \mathbf{\mu}, \mathbf{\pi}) = \prod_{n = 1}^N \prod_{k = 1}^K \left( \pi_k \prod_{i = 1}^D \mu_{k, i}^{x_{n, i}} (1 - \mu_{k, i})^{1 - x_{n, i}} \right)^{z_{n, k}}.\end{align}

이에 로그함수를 취하면 완전한 데이터 로그가능도(complete data log-likelihood^영어)

\mathcal{L}(\theta)

가 유도된다.

\begin{align}\mathcal{L}(\theta) = \ln \,\text{Pr}(\mathbf{X}, \mathbf{Z}| \mathbf{\mu}, \mathbf{\pi}) = \sum_{n = 1}^N \sum_{k = 1}^K z_{n, k} \left( \ln \pi_k + \sum_{i = 1}^D x_{n, i} \ln \mu_{k, i} + (1 - x_{n, i}) \ln (1 - \mu_{k, i}) \right).\end{align}

13. 2. 1. 기댓값 단계(E step)

기댓값 단계에서는 잠재변수

\mathbf{Z}

의 값을 업데이트하기 위해

\,\text{Pr}(\mathbf{Z} | \mathbf{X}, \mathbf{\theta})

확률분포를 사용한다. 이 분포는 정확히 풀 수 없으므로, 현재

z_{n, k}

값을 해당 변수의 기댓값으로 대체하여 추정한다.

\begin{align}z_{n, k}^\text{new} \leftarrow \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \mathbf{\mu}, \mathbf{\pi}}[z_{n, k}] = \sum_{z_{n, k}} \,\text{Pr}(z_{n,k} | \mathbf{x_n}, \mathbf{\mu}, \mathbf{\pi}) \, z_{n,k} = \frac{\pi_k \,\text{Pr}(\mathbf{x_n} |\mathbf{\mu_k})}{\sum_{m = 1}^K \pi_m \,\text{Pr}(\mathbf{x_n} | \mathbf{\mu_m})} = \frac{\pi_k \prod_{i = 1}^D \mu_{k, i}^{x_{n, i}} (1 - \mu_{k, i})^{1 - x_{n, i}} }{\sum_{m = 1}^K \pi_m \prod_{i = 1}^D \mu_{m, i}^{x_{n, i}} (1 - \mu_{m, i})^{1 - x_{n, i}}}.\end{align}

이러한 방식으로

z_{n,k}

값을 업데이트하면 잠재변수

\mathbf{z_{n}}^\text{new}

는 더 이상 1-of-

K

형태로 표현되지 않는다. 이는 이미지

\mathbf{x_{n}}

이 하나의 군집에 속하는 것이 아니라 여러 군집에 부분적으로 속한다는 것을 의미한다.

13. 2. 2. 최대화 단계(M step)

이 모델의 모수들(혼합 계수 및 군집별 픽셀 분포 변수)을 최대화하기 위해 다음 식을 이용한다.

\mathbf{\theta}^\text{new} \leftarrow \underset{\mathbf{\theta}}{\text{arg max }} \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \theta^\text{old}} \left[ \mathcal{L}(\theta) \right]

\begin{align}\mathbb{E}_{\mathbf{Z} | \mathbf{X}, \theta^\text{old}} \left[ \mathcal{L}(\theta) \right] &= \sum_{n = 1}^N \sum_{k = 1}^K \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \mathbf{\mu}^\text{old}, \mathbf{\pi}^\text{old}} \left[ z_{n, k} \right] \left( \ln \pi_k + \sum_{i = 1}^D x_{n, i} \ln \mu_{k, i} + (1 - x_{n, i}) \ln (1 - \mu_{k, i}) \right).\end{align}

위 식을

\mathbf{\mu_k}

에 관해 최대화하기 위해 미분하여

0

이 되는 값을 찾는다.

\begin{align}\frac{\partial}{\partial \mu_{m, j}} \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \theta^\text{old}} \left[ \mathcal{L}(\theta) \right] &= \sum_{n = 1}^N \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \mathbf{\mu}^\text{old}, \mathbf{\pi}^\text{old}} \left[ z_{n, m} \right] \left( \frac{x_{n, j}}{\mu_{m, j}} - \frac{1 - x_{n, j}}{1 - \mu_{m, j}} \right) \\&= \sum_{n = 1}^N z_{n, m}^\text{new} \frac{x_{n, j} - \mu_{m, j}}{\mu_{m, j} (1 - \mu_{m, j})} = 0 \Leftrightarrow \\\mu_{m, j} &= \frac{1}{N_m} \sum_{n = 1}^N x_{n, j} z_{n, m}^\text{new},\end{align}

이 때,

N_m = \sum_{n = 1}^N z_{n, m}^\text{new}

는 군집

m

에 실질적으로 속한 이미지의 개수이다.

군집

m

에서의 픽셀 분포의 매개변수

\mathbf{\mu_m}

는 다음과 같이 나타낼 수 있다.

\mathbf{\mu_m} = \mathbf{\bar{x}_m}, \mathbf{\bar{x}_m} = \frac{1}{N_m} \sum_{n = 1}^N z_{n, m}^\text{new} \mathbf{x_n}

\mathbf{\bar{x}_m}

는 군집

m

에 (실질적으로) 속한 이미지들의 가중 평균을 의미한다.

\mathbb{E}_{\mathbf{Z} | \mathbf{X}, \theta^\text{old}} \left[ \mathcal{L}(\theta) \right]

를 혼합 계수

\mathbf{\pi}

와 조건

\sum_{k = 1}^K \pi_k = 1

에 관해 최대화하기 위해 라그랑주 승수법(Lagrange Multiplier)을 이용한다.

\Lambda(\theta, \lambda) := \mathbb{E}_{\mathbf{Z} | \mathbf{X}, \theta^\text{old}} \left[ \mathcal{L}(\theta) \right] + \lambda \left( \sum_{k = 1}^K \pi_k - 1 \right)

최댓값은 다음과 같이 구할 수 있다.

\begin{align}\frac{\partial}{\partial \pi_{m}} \Lambda(\theta, \lambda) = \frac{1}{\pi_m} \sum_{n = 1}^N z_{n,m}^\text{new} + \lambda = 0 \Leftrightarrow \\\pi_m = -\frac{N_m}{\lambda},\end{align}

\begin{align}\frac{\partial}{\partial \lambda} \Lambda(\theta, \lambda) = \sum_{k = 1}^K \pi_k - 1 = 0 \Leftrightarrow \\\sum_{k = 1}^K \pi_k = 1.\end{align}

위 두 결과를 종합하면

\lambda = - \sum_{k = 1}^K N_k = - N

이고,

\pi_m = -\frac{N_m}{\lambda} = \frac{N_m}{N}

이다.

13. 2. 3. 요약

베르누이 혼합 모델의 기댓값 단계(E step)에서는 다음과 같은 수식을 사용한다.

z_{n, k} \leftarrow \frac{\pi_k \prod_{i = 1}^D \mu_{k, i}^{x_{n, i}} (1 - \mu_{k, i})^{1 - x_{n, i}} }{\sum_{m = 1}^K \pi_m \prod_{i = 1}^D \mu_{m, i}^{x_{n, i}} (1 - \mu_{m, i})^{1 - x_{n, i}}}

최대화 단계(M step)에서는 다음 수식을 사용하여

\mathbf{\mu_m}

와

\pi_m

을 업데이트한다.

\mathbf{\mu_m} \leftarrow \mathbf{\bar{x}_m}

,

\pi_m \leftarrow \frac{N_m}{N}

이때,

\mathbf{\bar{x}_m} = \frac{1}{N_m} \sum_{n = 1}^N z_{n, m} \mathbf{x_n}

이고,

N_m = \sum_{n = 1}^N z_{n, m}

이다.

14. EM의 대체 알고리즘

EM은 일반적으로 수렴 속도에 제한 없이 반드시 전역 최적해가 아닌 지역 최적해로 수렴한다. 고차원에서는 임의로 성능이 저하될 수 있고 지수적으로 많은 국소 최적해가 있을 수 있다. 따라서 특히 고차원 설정에서는 보장된 학습을 위한 대안적인 방법이 필요하다. EM에 대한 대안은 일관성에 대한 더 나은 보장을 제공하며, '모멘트 기반 접근 방식' 또는 소위 '스펙트럼 기법'이라고 한다. 확률 모델의 매개변수를 학습하는 모멘트 기반 접근 방식은 국소 최적해에 갇히는 문제가 자주 발생하는 EM과는 달리 특정 조건에서 전역 수렴과 같은 보장을 제공한다. 학습에 대한 보장을 제공하는 알고리즘은 혼합 모델, 은닉 마르코프 모델(HMM) 등과 같은 여러 중요한 모델에서 도출될 수 있다. 이러한 스펙트럼 방법의 경우 가짜 국소 최적해가 발생하지 않으며, 몇 가지 규칙적인 조건에서 실제 매개변수를 일관되게 추정할 수 있다.^{[ko-21]저널 Tensor decompositions for learning latent variable models}^{[ko-22]저널 A method of moments for mixture models and hidden Markov models}^{[ko-23]저널 A tensor approach to learning mixed membership community models}

EM은 극값으로만 수렴하고 일반적으로 수렴율에 대한 범위가 없다. 고차원에서 잘 작동하지 않고 극값의 수가 다수가 존재할 가능성이 있다. 따라서 특히 고차원 상에서 다른 학습 방법을 사용할 필요가 있다. 이 때 모멘트-기반 접근 방식이나 스펙트럼 기법이 더 좋은 효과를 보장한다. 모멘트-기반 접근은 확률 모형의 매개변수를 학습하기 위한 것으로 최근 들어 사용이 많아지기 시작했는데, 이는 EM이 극값만을 보장해주는 것에 반해 모멘트-기반 접근은 최대, 최솟값을 보장하기 때문이다.

15. 추가 자료

트레버 헤이스티(Trevor Hastie), 로버트 티브시라니(Robert Tibshirani), 제롬 프리드먼(Jerome Friedman)의 저서 ''통계적 학습의 기초 - 데이터 마이닝, 추론, 예측'' (2014)이 있다.
C.M. 비숍(C.M. Bishop)의 ''패턴 인식과 기계 학습 하 (베이즈 이론에 의한 통계적 예측)'' (2012)이 있다.
왕진팡(汪金芳), 데즈카 슈(手塚集), 우에다 오사무노리(上田修功), 다구리 마사아키(田栗正章), 카바시마 요시유키(樺島祥介), 아마리 슌이치(甘利俊一), 다케무라 아키미치(竹村彰通), 다케우치 케이(竹内啓), 이바 유키토(伊庭幸人)가 공동 저술한 ''계산 통계 I - 확률 계산의 새로운 기법'' (2003)이 있다.^{[ko-1]저널 Maximum likelihood theory for incomplete data from an exponential family}
로버트 호그(Robert Hogg), 조셉 맥케인(Joseph McKean), 앨런 크레이그(Allen Craig)의 ''Introduction to Mathematical Statistics'' (2005)의 359-364쪽에 관련 내용이 있다.
데이비드 J.C. 매케이(David J.C. MacKay)의 온라인 교과서 [http://www.inference.phy.cam.ac.uk/mackay/itila/ 정보 이론, 추론 및 학습 알고리즘]에는 소프트 K-평균 알고리즘을 사용한 클러스터링과 같은 EM 알고리즘의 예시와 변분적 관점이 설명되어 있다.
제프 빌메스(Jeff Bilmes)가 작성한 [http://citeseer.ist.psu.edu/bilmes98gentle.html EM 알고리즘에 대한 튜토리얼]에는 가우시안 혼합 및 은닉 마르코프 모델에 대한 매개변수 추정 적용이 설명되어 있다.
M.J. 비얼(M. J. Beal)의 [http://www.cse.buffalo.edu/faculty/mbeal/thesis/index.html 근사 베이지안 추론을 위한 변분 알고리즘]에서는 EM 알고리즘과 변분 베이지안 EM을 비교하고 변분 베이지안 HMM을 포함한 여러 모델을 유도한다.
프랭크 델라에르트(Frank Dellaert)의 [http://www.cc.gatech.edu/~dellaert/em-paper.pdf 기대 최대화 알고리즘]에서는 하한 최대화 측면에서 EM 알고리즘을 설명한다.
숀 보먼(Sean Borman)의 [http://www.seanborman.com/publications/EM_algorithm.pdf 기대 최대화 알고리즘: 짧은 튜토리얼]에서는 EM 알고리즘을 자체적으로 유도한다.
샤오진 주(Xiaojin Zhu)의 [http://pages.cs.wisc.edu/~jerryzhu/cs838/EM.pdf EM 알고리즘]도 참고할 수 있다.
제프리 J. 맥라클란(Geoffrey J. McLachlan)과 트리얌바캄 크리슈난(Thriyambakam Krishnan)의 저서 "The EM Algorithm and Extensions" (1997)과 2판 (2008)이 있다.
고니시 사다노리(小西貞則), 오치 요시미치(越智義道), 오모리 히로야스(大森裕浩)의 ''계산 통계학의 방법 - 부트스트랩, EM 알고리즘, MCMC-'' (2008)이 있다.
세키하라 겐스케(関原謙介)의 ''베이즈 신호 처리'' (2015)와 [http://signalanalysis.jp/pdfs/Bayes2019_0807.pdf 베이즈 추론의 기초와 신호 처리 응용] 자료가 있다.
케네스 랭(Kenneth Lange)의 "MM 최적화 알고리즘" (2016)에서는 MM 알고리즘(MM algorithm)이 EM 알고리즘의 일반화로 제시된다.
구로다 마사히로(黒田正博)의 ''EM 알고리즘'' (2020)이 있다.
크리스토퍼 M. 비숍(Christopher M. Bishop)의 ''Pattern Recognition and Machine Learning''(2006)도 참고할 만하다.^{[ko-2]논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University}
M. R. Gupta와 Y. Chen의 "Theory and Use of the EM Algorithm" (2010)이 있다.
알렉시스 로슈(Alexis Roche)의 [http://arxiv.org/pdf/1105.1476.pdf EM algorithm and variants: an informal tutorial]에서는 EM과 여러 변형 알고리즘을 설명한다.
G.A. Einicke의 "Smoothing, Filtering and Prediction: Estimating the Past, Present and Future" (2012)도 관련 자료이다.

참조

_[en-1] 논문 The EM algorithm – an old folk-song sung to a fast new tune 1997
_[en-2] 간행물 Proceedings of the Twenty Third International Conference on Artificial Intelligence and Statistics PMLR 2020
_[en-3] 논문 Maximum Likelihood from Incomplete Data via the EM Algorithm
_[en-4] 논문 The estimation of gene frequencies in a random-mating population
_[en-5] 논문 Maximum Likelihood estimation from incomplete data 1958
_[en-6] 서적 The EM Algorithm http://dx.doi.org/10[...] Springer Berlin Heidelberg 2022-10-15
_[en-7] 논문 Maximum likelihood theory for incomplete data from an exponential family
_[en-8] 학위논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University 1971
_[en-9] 논문 An iterative method for solution of the likelihood equations for incomplete data from exponential families
_[en-10] 기타
_[en-11] 기타 Statistics from the point of view of statistical mechanics Mathematical Institute, Aarhus University 1966
_[en-12] 기타 Statistiska Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Lecture notes 1969-1970), with the assistance of Rolf Sundberg. Stockholm University 1970
_[en-13] 기타 The notion of redundancy and its use as a quantitative measure of the deviation between a statistical hypothesis and a set of observational data. Aarhus 1973
_[en-14] 논문 The notion of redundancy and its use as a quantitative measure of the discrepancy between a statistical hypothesis and a set of observational data
_[en-15] 논문 On the Convergence Properties of the EM Algorithm 1983-03
_[en-16] 논문 Convergence of Expectation-Maximization Algorithm With Mixed-Integer Optimization https://ieeexplore.i[...] 2024-04-24
_[en-17] 서적 Statistical Modelling by Exponential Families Cambridge University Press 2019
_[en-18] 서적 Encyclopedia of Statistical Sciences Wiley 2006
_[en-19] 서적 Statistical Analysis with Missing Data https://archive.org/[...] John Wiley & Sons
_[en-20] 논문 Inferring neural activity before plasticity as a foundation for learning beyond backpropagation 2024-02
_[en-21] 서적 Learning in Graphical Models http://ftp.cs.toront[...] MIT Press 2009-03-22
_[en-22] 서적 The Elements of Statistical Learning https://archive.org/[...] Springer
_[en-23] 논문 Newton—Raphson and EM Algorithms for Linear Mixed-Effects Models for Repeated-Measures Data
_[en-24] 논문 Fitting Mixed-Effects Models Using Efficient EM-Type Algorithms
_[en-25] 논문 A new REML (parameter expanded) EM algorithm for linear mixed models
_[en-26] 논문 “STRIDE for Structural Identification using Expectation Maximization: Iterative Output-Only Method for Modal Identification.” http://ascelibrary.o[...] 2016
_[en-27] 논문 Censored expectation maximization algorithm for mixtures: Application to intertrade waiting times https://www.scienced[...] 2022
_[en-28] 논문 Riccati Equation and EM Algorithm Convergence for Inertial Navigation Alignment 2009-01
_[en-29] 논문 EM Algorithm State Matrix Estimation for Navigation 2010-05
_[en-30] 논문 Iterative Smoother-Based Variance Estimation 2012-05
_[en-31] 논문 Iterative Filtering and Smoothing of Measurements Possessing Poisson Noise 2015-09
_[en-32] 논문 Acceleration of the EM Algorithm by using Quasi-Newton Methods
_[en-33] 논문 Parameter expansion to accelerate EM: The PX-EM algorithm
_[en-34] 논문 Maximum likelihood estimation via the ECM algorithm: A general framework
_[en-35] 논문 The ECME Algorithm: A Simple Extension of EM and ECM with Faster Monotone Convergence
_[en-36] 간행물 Accelerating Expectation–Maximization Algorithms with Frequent Updates http://rio.ecs.umass[...]
_[en-37] 논문 A Tutorial on MM Algorithms http://www.stat.psu.[...] 2004
_[en-38] 논문 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures
_[en-39] 논문 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs
_[en-40] 논문 Maximum likelihood estimation in a linear model from confined and censored normal data
_[en-41] 논문 Contributions to the Mathematical Theory of Evolution 1894
_[en-42] 간행물 Learning Latent Variable Models by Improving Spectral Solutions with Exterior Point Method https://www.cc.gatec[...] 2019-06-12
_[en-43] 서적 Local Loss Optimization in Operator Models: A New Insight into Spectral Learning 2012-06-27
_[en-44] 웹사이트 The MM Algorithm http://www.stat.berk[...]
_[ja-1] 서적 PRML
_[ja-2] 서적 ESL
_[ja-3] 논문 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures
_[ja-4] 논문 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs
_[ja-5] 논문 Maximum Likelihood from Incomplete Data via the EM Algorithm
_[ko-1] 저널 Maximum likelihood theory for incomplete data from an exponential family
_[ko-2] 논문 Maximum likelihood theory and applications for distributions generated when observing a function of an exponential family variable Institute for Mathematical Statistics, Stockholm University
_[ko-3] 저널 An iterative method for solution of the likelihood equations for incomplete data from exponential families
_[ko-4] 서적 Contributions to the theory of estimation from grouped and partially grouped samples Almqvist & Wiksell
_[ko-5] 논문 "Utvärdering av livslängder i subnanosekundsområdet" ("Evaluation of sub-nanosecond lifetimes")
_[ko-6] 논문 Statistics from the point of view of statistical mechanics Mathematical Institute, Aarhus University
_[ko-7] 논문 Statistika Modeller (Statistical Models): Anteckningar från seminarier läsåret 1969–1970 (Notes from seminars in the academic year 1969-1970), with the assistance of Rolf Sundberg. Stockholm University
_[ko-8] 간행물 The notion of redundancy and its use as a quantitative measure of the deviation between a statistical hypothesis and a set of observational data.
_[ko-9] 저널 The notion of redundancy and its use as a quantitative measure of the discrepancy between a statistical hypothesis and a set of observational data.
_[ko-10] 서적 Statistical Analysis with Missing Data https://archive.org/[...] John Wiley & Sons
_[ko-11] 저널 A view of the EM algorithm that justifies incremental, sparse, and other variants ftp://ftp.cs.toronto[...] MIT Press 2009-03-22
_[ko-12] 서적 The Elements of Statistical Learning https://archive.org/[...] Springer
_[ko-13] 저널 Riccati Equation and EM Algorithm Convergence for Inertial Navigation Alignment 2009-01
_[ko-14] 저널 EM Algorithm State Matrix Estimation for Navigation 2010-05
_[ko-15] 저널 Iterative Smoother-Based Variance Estimation 2012-05
_[ko-16] 저널 Acceleration of the EM Algorithm by using Quasi-Newton Methods
_[ko-17] 저널 Maximum likelihood estimation via the ECM algorithm: A general framework https://archive.org/[...]
_[ko-18] 저널 A Tutorial on MM Algorithms http://www.stat.psu.[...] 2011-07-20
_[ko-19] 저널 The α-EM algorithm: Surrogate likelihood maximization using α-logarithmic information measures
_[ko-20] 저널 Hidden Markov model estimation based on alpha-EM algorithm: Discrete and continuous alpha-HMMs
_[ko-21] 저널 Tensor decompositions for learning latent variable models
_[ko-22] 저널 A method of moments for mixture models and hidden Markov models https://archive.org/[...]
_[ko-23] 저널 A tensor approach to learning mixed membership community models
_[ko-24] 웹인용 The MM Algorithm http://www.stat.berk[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com