맨위로가기

캣멀롬 스플라인

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

캣멀롬 스플라인은 네 개의 제어점과 노트를 사용하여 정의되는 곡선이다. 이 곡선은 주어진 점들을 부드럽게 연결하며, 0에서 1 사이의 알파 값을 통해 다양한 형태를 가질 수 있다. 파이썬으로 구현된 코드 예제를 통해 캣멀롬 스플라인의 사용법을 확인할 수 있다.

광고

더 읽어볼만한 페이지

  • 스플라인 - 스플라인 보간법
    스플라인 보간법은 주어진 데이터 점들을 부드럽게 연결하는 곡선을 생성하는 방법으로, 원래 기술 도면을 그릴 때 사용된 탄성 자에서 유래되었으며, 수학적으로는 일련의 다항식을 사용하여 곡선을 모델링하고, 3차 스플라인을 포함한 다양한 형태가 존재하며, 컴퓨터 그래픽스 등 다양한 분야에서 활용된다.
  • 스플라인 - B-스플라인 곡선
    B-스플라인 곡선은 제어점을 연결하여 부드러운 곡선을 생성하는 수학적 표현 방식이며, B-스플라인 기저 함수와 제어점의 선형 결합으로 표현되고, 매듭의 배치에 따라 균일, 개방 균일, 비균일 B-스플라인으로 분류되며, CAD, 컴퓨터 그래픽스 등 다양한 분야에서 활용된다.

2. 정의

배리와 골드만의 피라미드 공식


캣멀롬 알고리즘에서의 노트 매개변수화


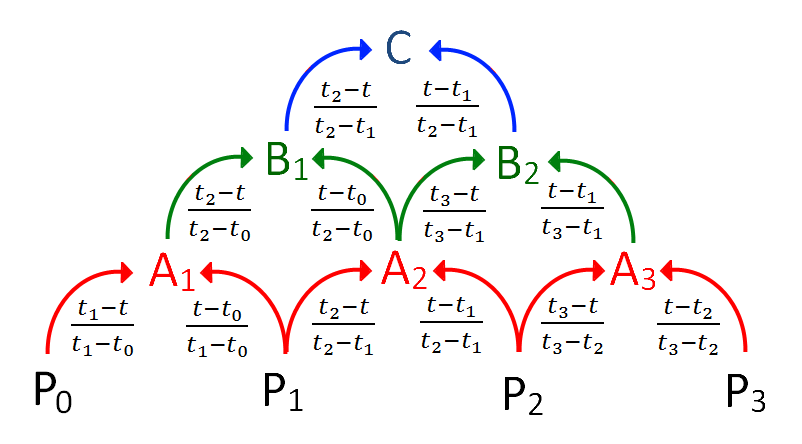
점은 \mathbf{P}_i = [x_i \quad y_i]^T와 같이 표현하기로 하자. 네 개의 점 \mathbf{P}_0, \mathbf{P}_1, \mathbf{P}_2, \mathbf{P}_3과 노트 t_0, t_1, t_2, t_3으로 정의되는 곡선 일부 '''C'''(캣멀롬 스플라인)는 다음과 같이 표현할 수 있다:

:\mathbf{C} = \frac{t_{2}-t}{t_{2}-t_1}\mathbf{B}_1+\frac{t-t_1}{t_{2}-t_1}\mathbf{B}_2

이는 다음과 같다.

:\mathbf{B}_1 = \frac{t_{2}-t}{t_{2}-t_0}\mathbf{A}_1+\frac{t-t_0}{t_{2}-t_0}\mathbf{A}_2

:\mathbf{B}_2 = \frac{t_{3}-t}{t_{3}-t_1}\mathbf{A}_2+\frac{t-t_1}{t_{3}-t_1}\mathbf{A}_3

:\mathbf{A}_1 = \frac{t_{1}-t}{t_{1}-t_0}\mathbf{P}_0+\frac{t-t_0}{t_{1}-t_0}\mathbf{P}_1

:\mathbf{A}_2 = \frac{t_{2}-t}{t_{2}-t_1}\mathbf{P}_1+\frac{t-t_1}{t_{2}-t_1}\mathbf{P}_2

:\mathbf{A}_3 = \frac{t_{3}-t}{t_{3}-t_2}\mathbf{P}_2+\frac{t-t_2}{t_{3}-t_2}\mathbf{P}_3

또한

:t_{i+1} = \left[\sqrt{(x_{i+1}-x_i)^2+(y_{i+1}-y_i)^2}\right]^{\alpha} + t_i

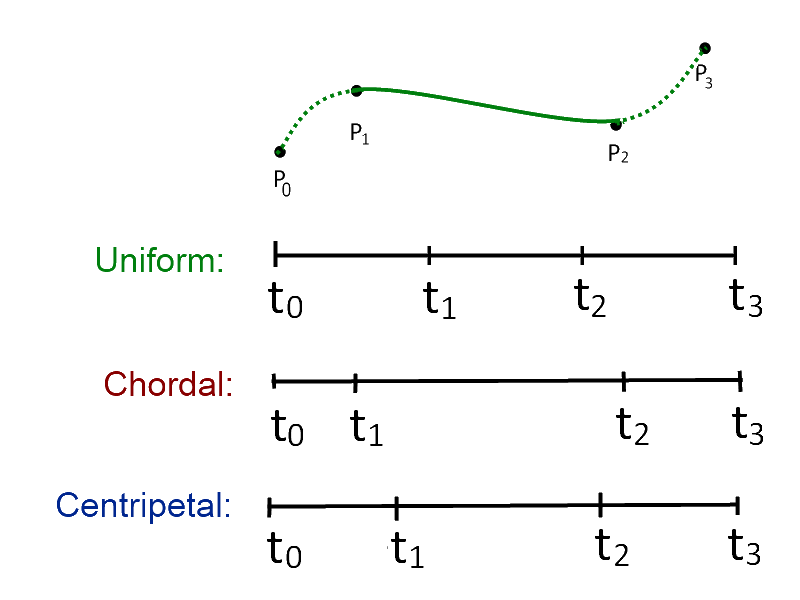
노트 매개변수화에서 \alpha가 0부터 1 사이의 범위를 가지고 i = 0,1,2,3 일 때 t_0 = 0 이다. 구심적(centripetal) 캣멀롬 스플라인에서 \alpha 값은 0.5이다. \alpha = 0일 때, 곡선은 표준(uniform) 캣멀롬 스플라인의 모양을 가진다. \alpha = 1일 때, 코달(chordal) 스플라인의 모양을 가진다.

3. 코드 예제

python

import numpy

import pylab as plt

def CatmullRomSpline(P0, P1, P2, P3, nPoints=100):

"""

P0, P1, P2, P3는 캣멀롬 스플라인을 정의하는 (x, y) 점 쌍이어야 합니다.

nPoints는 이 곡선 세그먼트에 포함할 점의 개수입니다.

"""

# 점들을 numpy 배열로 변환하여 배열 곱셈을 할 수 있도록 합니다.

P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])

# t0부터 t4까지 계산합니다.

alpha = 0.5

def tj(ti, Pi, Pj):

xi, yi = Pi

xj, yj = Pj

return ( ( (xj-xi)2 + (yj-yi)2 )0.5 )alpha + ti

t0 = 0

t1 = tj(t0, P0, P1)

t2 = tj(t1, P1, P2)

t3 = tj(t2, P2, P3)

# P1과 P2 사이의 점만 계산합니다.

t = numpy.linspace(t1,t2,nPoints)

# P0부터 P3까지의 점들과 곱하여 t의 각 값에 대한 점을 얻을 수 있도록 형태를 변경합니다.

t = t.reshape(len(t),1)

A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1

A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2

A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3

B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2

B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3

C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2

return C

def CatmullRomChain(P):

"""

일련의 점들에 대한 캣멀롬 스플라인을 계산하고 결합된 곡선을 반환합니다.

"""

sz = len(P)

# 곡선 C는 (x, y) 점들의 배열을 포함합니다.

C = []

for i in range(sz-3):

c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3])

C.extend(c)

return C

# 곡선이 통과할 점들의 집합을 정의합니다.

Points = 0,1.5],[2,2],[3,1],[4,0.5],[5,1],[6,2],[7,3

# 점들을 통과하는 캣멀롬 스플라인을 계산합니다.

c = CatmullRomChain(Points)

# 캣멀롬 곡선 점들을 x와 y 배열로 변환하고 플롯합니다.

x,y = zip(*c)

plt.plot(x,y)

# 제어점을 플롯합니다.

px, py = zip(*Points)

plt.plot(px,py,'or')

plt.show()


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com