피츠의 법칙

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 공식
- 2.1. 섀넌 공식
- 2.2. 정확도 조정을 위한 공식
3. 모델의 발전
- 3.1. Welford의 모델
- 3.2. 2차원 모델
4. UI 디자인에의 시사점
5. 비판 및 한계
참조

1. 개요

피츠의 법칙은 목표물까지의 거리와 목표물의 크기가 동작 시간에 미치는 영향을 설명하는 인간-컴퓨터 상호작용 분야의 중요한 법칙이다. 이 법칙은 목표물까지의 거리가 멀어질수록, 목표물의 크기가 작아질수록 동작 시간이 증가한다는 것을 수학적으로 나타낸다. 섀넌 공식으로 표현되며, GUI 디자인에 중요한 시사점을 제공하여, 버튼 크기, 화면 모서리 활용, 팝업 메뉴 사용 등 인터페이스 설계를 위한 지침으로 활용된다. 피츠의 법칙은 다양한 조건에서도 적용 가능하며, HCI 분야에서 널리 연구되고 활용되고 있다.

더 읽어볼만한 페이지

인간공학 - 신뢰성 공학
신뢰성 공학은 제품이나 시스템이 정해진 기간 동안 지정된 조건에서 의도된 기능을 수행할 확률을 다루는 공학 분야이며, 확률, 의도된 기능, 기간, 조건을 고려하여 시스템의 신뢰성을 높이고, 신뢰성 시험 및 다양한 기법을 활용하여 안전 공학 및 제조업 분야에서 중요한 역할을 한다.
인간공학 - 스트레스 볼
스트레스 볼은 손으로 쥐었다 놓는 행위를 통해 스트레스 해소를 돕는 완구로, 다양한 재질과 형태로 제작되며 물리 치료에서는 재활 훈련 및 통증 완화에 사용된다.
인간-컴퓨터 상호 작용 - 페이스북
페이스북은 마크 저커버그가 2004년 공동 창업한 소셜 네트워킹 서비스로, 전 세계적인 확장과 다양한 기능 추가, 사업 영역 확장을 거쳤으나, 개인정보 문제 및 논란으로 비판받았고, 2021년 메타 플랫폼즈로 사명을 변경하며 메타버스 구축에 집중하고 있다.
인간-컴퓨터 상호 작용 - 인터넷 익스플로러
마이크로소프트가 개발한 웹 브라우저인 인터넷 익스플로러는 윈도우 운영 체제와의 통합으로 높은 시장 점유율을 유지했으나, 웹 표준 문제와 보안 취약점으로 비판받으며 2015년 엣지에 자리를 내주고 2022년 지원이 종료되었지만, 엣지의 IE 모드로 레거시 호환성을 유지하고 있다.
사람 이름을 딴 낱말 - 뒤베르제의 법칙
뒤베르제의 법칙은 선거제도와 정당 수 사이의 관계를 설명하는 가설로, 단순 다수 대표제는 양당제를, 결선투표제와 비례대표제는 다당제를 낳는다는 내용을 제시한다.
사람 이름을 딴 낱말 - 옴의 법칙
옴의 법칙은 1827년 게오르크 옴이 발표한, 전압(V)은 전류(I)와 저항(R)의 곱(V=IR)으로 표현되는, 전압, 전류, 저항 간의 관계를 나타내는 기본 법칙이다.

피츠의 법칙
개요
이름	피츠의 법칙 (Fitts's law)
로마자 표기	Picheuibeopchik
유형	예측 모델
분야	인간 운동
내용
설명	목표물까지의 거리와 목표물의 크기에 따라 움직임 시간이 예측 가능하다는 법칙이다.
관련 분야	인간-컴퓨터 상호 작용 (HCI) 인체공학
공식	MT = a + b log2(2A/W)
공식 설명	MT = 움직임 시간 (Movement Time) a, b = 장비에 따른 경험적으로 얻는 상수 A = 움직임의 진폭 (Amplitude) W = 목표물의 폭 (Width)
공식 간략화	MT = a + b ID
간략화 공식 설명	ID = 난이도 지수 (Index of Difficulty)
변수
진폭 (A)	시작 위치에서 목표 중심까지의 거리
폭 (W)	움직임 방향으로 측정한 목표 크기
특징
적용 가능성	다양한 입력 장치 (마우스, 터치스크린, 스타일러스 등)
적용 분야	웹 디자인, 소프트웨어 인터페이스 디자인
예시	메뉴 디자인 시, 자주 사용하는 기능은 크게 만들어 접근성을 높임 버튼 간 간격을 넓혀 클릭 정확도를 높임
영향 요인
신체 부위	손, 발, 입술, 머리
환경	수중 환경
개인차	나이 성별 운동 능력 학습 장애 약물 (마리화나)

2. 공식

피츠의 법칙은 여러 방법으로 공식화되었는데, 그중 가장 대표적인 것은 스코트 매켄지가 제안한 샤논 공식이다.

: $T = a + b \log_2 \left(\frac{2D}{W} \right)$

''T''는 동작을 완수하는 데 필요한 평균 시간으로, ''MT''(Movement Time)라고도 한다.
''a'' 와 ''b''는 실험 상수로서, 데이터를 측정하여 얻어진 실험치로 결정된다.
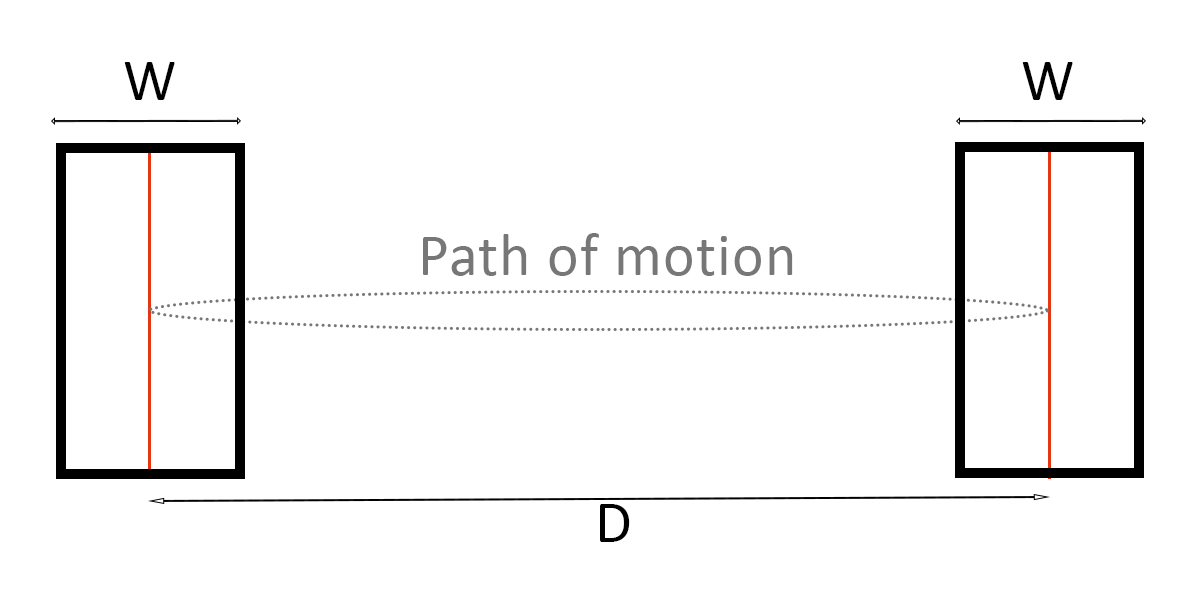
''D''는 대상 물체의 중심으로부터 측정한 거리로, ''A''(Amplitude)라고도 한다.
''W''는 움직이는 방향을 축으로 하였을 때 측정되는 목표물의 폭이다. ''W''는 최종 목표치에 다다를 때 허용되는 오차치이기도 하다.

이 공식에서 목표물의 크기가 작아질수록 속도와 정확도가 나빠지고, 목표물과의 거리가 멀어질수록 필요한 시간이 더 길어진다는 것을 알 수 있다.

폴 피츠는 1954년 논문에서 대상 선택 작업의 난이도 지표(ID, 비트 단위)를 제안했다.

:

\text{ID} = \log_2 \Bigg(\frac{2D} {W}\Bigg)

피츠는 또한 인간의 수행 능력을 측정하기 위해 ''수행 지수''(IP, 초당 비트 단위)를 제안했다. 이 지표는 작업의 난이도 지수(''ID'')와 대상 선택에 걸리는 이동 시간(''MT'', 초 단위)을 결합한다.

:

\text{IP} = \Bigg(\frac{\text{ID}} {\text{MT}}\Bigg)

오늘날, ''IP''는 더 일반적으로 ''처리량''(TP)이라고 불린다.

피츠 이후 연구자들은 선형 회귀 방정식을 구축하고 적합도를 위해 상관관계(''r'')를 검토하는 방식을 시작했다.

:

\text{MT} = a + b \cdot \text{ID} = a + b \cdot \log_2 \Bigg(\frac{2D}{W}\Bigg)

''MT''는 동작을 완료하는 데 걸리는 평균 시간이다.
''a''와 ''b''는 입력 장치 선택에 따라 달라지는 상수이며, 일반적으로 회귀 분석을 통해 경험적으로 결정된다.
''ID''는 난이도 지수이다.
''D''는 시작점에서 대상의 중심까지의 거리이다.
''W''는 동작 축을 따라 측정한 대상의 너비이다.

''b'' 매개변수의 값은 컴퓨터 포인팅 장치를 서로 비교할 때 지표로 사용될 수 있다. 피츠의 법칙의 첫 번째 인간-컴퓨터 인터페이스 응용 프로그램은 Card, English, Burr에 의해 이루어졌으며,^[11] 이들은 1/''b'' 로 해석되는 수행 지수(''IP'')를 사용하여 다양한 입력 장치의 성능을 비교했는데, 마우스가 조이스틱이나 방향 이동 키에 비해 최고 성능을 보였다.^[11]

피츠의 법칙은 다양한 동작 모델로부터 도출될 수 있다. 예를 들어 사용자가 작은 동작을 연속하여 목표 지점으로 이동한다고 가정하고, 각각의 작은 동작은 일정 시간 ''t''가 소요되며 목표 중심까지 남은 거리에 대해 일정 비율 1 -''r'' ( 0 < ''r'' < 1 )을 이동한다고 하자. 사용자의 첫 번째 작은 동작 후 남은 거리는 ''rD''가 되며, n번째 작은 동작 후에는 ''rⁿD''가 된다. ''N''을 도달에 필요한 작은 동작 횟수라고 하면,

:

r^N D = \frac{W}{2}

가 된다. 이것을 N에 대해 풀면,

:

\begin{align}N & = \log_r \frac{W}{2D} \\& = \frac{1}{\log_2 r} \log_2 \frac{W}{2D} \\& = \frac{1}{\log_2 1/r} \log_2 \frac{2D}{W}\end{align}

모든 작은 동작 완료에 필요한 시간은,

:

\begin{align}T = Nt & = \frac{t}{\log_2 1/r} \log_2 \frac{2D}{W} \\& = \frac{t}{\log_2 1/r} + \frac{t}{\log_2 1/r} \log_2 \frac{D}{W}\end{align}

적절한 상수 ''a'', ''b''를 정의하면, 위 식은 다음과 같이 변경된다.

:

T = a + b \log_2 \frac{D}{W}

2. 1. 섀넌 공식

수학적으로 피츠의 법칙은 몇 가지 다른 방법으로 공식화할 수 있는데, 가장 대표적인 것은 요크 대학교 교수 스코트 매켄지가 제안한 섀넌 공식이다.^[15]^[16]

:

T = a + b \log_2 \left(1 + \frac{D}{W} \right)

여기서:

''T''는 동작을 완료하는 평균 시간이다. (전통적으로 이 분야의 연구자는 이동 시간(movement time)을 의미하는 ''MT''를 사용한다)
''a''는 장치의 시작・정지 시간을 나타내고, ''b''는 장치 자체의 속도이다. 이들은 계측 데이터의 직선 근사에 의해 구해진다.
''D''는 시작점에서 대상의 중심까지의 거리이다 (전통적으로 이 분야의 연구자는 움직임의 폭 amplitude를 의미하는 ''A''를 사용한다)
''W''는 움직임의 방향으로 측정한 대상의 폭이다. ''W''는 동작의 최종 지점이 대상의 중심에서 ± 내에 있어야 하므로, 최종적인 위치에 대해 허용되는 오차로 생각할 수 있다.

위 식에서, 목표가 멀리 있거나 작을 경우 더 많은 시간이 걸리는 "속도와 정확성"의 트레이드 오프를 볼 수 있다.

이 공식은 섀넌-하틀리 정리와 유사하기 때문에 이러한 이름이 붙었다.^[16] 이 정리는 대역폭, 신호 강도 및 잡음을 사용하여 정보 전송을 설명한다. 피츠의 법칙에서 거리는 신호 강도를 나타내고, 목표 폭은 잡음을 나타낸다.

피츠의 난이도 지수를 표현하는 방식 중 인간-컴퓨터 상호 작용 분야에서 가장 널리 사용되는 것은 섀넌 공식이다.

:

\text{ID} = \log_2 \Bigg(\frac{D}{W}+1\Bigg)

이 모델을 사용하면, 포인팅 작업의 난이도는 작업을 수행함으로써 전송되는 정보량(비트 단위)과 동일하게 취급된다. 이는 포인팅이 정보 처리 작업으로 축약된다는 주장에 의해 정당화되었다. 피츠의 법칙과 영감을 준 섀넌-하틀리 정리 사이에는 공식적인 수학적 연관성은 없지만, 정보 이론을 사용하여 운동 행위를 정량화하는 매력 때문에 섀넌 형태의 법칙이 광범위하게 사용되었다.^[17] 2002년에 ISO 9241이 발표되어 섀넌 형태의 피츠의 법칙 사용을 포함한 인간-컴퓨터 인터페이스 테스트에 대한 표준을 제공했다. 키보드에서 일련의 키 입력을 통해 전송되는 정보와 그러한 작업의 ''ID''가 의미하는 정보가 일치하지 않는 것으로 나타났다.^[18] 섀넌 엔트로피는 피츠의 법칙과 다른 정보 값을 생성한다. 저자들은 이러한 오차가 무시할 수 있으며, 알려진 엔트로피를 가진 장치 또는 인간의 정보 처리 능력을 측정하는 경우에만 고려해야 한다고 언급했다.

피츠의 법칙의 대수 항은, 목표 달성의 어려움 ''ID'' 라고 불리며, 단위는 비트이다. 이 법칙은 다음과 같이 표현할 수도 있다.

:

T = a + b ID,

여기서

:

ID = \log_2 \left(\frac{D}{W}+1\right)

이다. 즉, ''b'' 의 단위는 비트당 시간, 예를 들어 밀리초/비트이다. 상수 ''a''는 반응 시간, 또는 마우스를 클릭하는 데 필요한 시간을 포함하는 것으로 생각할 수 있다.

''a'' 와 ''b'' 는, 목표 지점을 가리키는 동작의 조건이 변화하면 변한다. 예를 들어 마우스와 스타일러스는 모두 목표 지점을 가리키는 데 사용되지만, ''a''와 ''b''는 각각 다르다.

성능 평가값 ''IP'' (처리율 ''TP'' 라고도 불린다)는, 차원이 단위 시간당 비트이며, 동작이 얼마나 빨리 완료될 수 있는지를 나타낸다. 특정 목표와는 무관하다.

''IP'' 의 정의에는 관례적으로 두 가지 방법이 있으며, ''IP'' = 1/''b'' 로 하거나 (이 경우, ''a'' 의 영향을 무시해 버린다), ''IP'' = ''ID''_average/''MT''_average 로 한다 (이 경우, 산출에 사용된 평균적인 ''ID''에 의존해 버린다). 두 가지 방법에 대한 논의는, Zhai의 논문 (2002년)을 참조하기 바란다. 어떤 정의가 사용되더라도, 다른 입력 장치에서 ''IP'' 를 측정함으로써, 각 장치의 목표 지점을 가리키는 동작에 대한 성능을 비교할 수 있다.

피츠의 원래 공식화는 샤논의 공식화와는 약간 달라서,

:

ID = \log_2 \left(\frac{2D}{W}\right)

였다. 여기서의 2는 특히 중요하지 않으며, ''ID'' 는 2를 고려하여 상수 ''a''、''b''를 변경하면 흡수할 수 있다. 샤논의 형식에서의 "+1"은, 특히 ''D''/''W''가 작은 경우에는, 피츠의 원래 식에 큰 영향을 주지 않는다.

샤논의 형식에는, ''ID''가 항상 음수가 아닌 것, 계측 결과에 더 잘 부합한다는 장점이 있다.

2. 2. 정확도 조정을 위한 공식

요크 대학교 교수 Scott MacKenzie가 제안한 샤논 공식은 다음과 같다.^[1]

:

T = a + b \log_2 \Bigg(1+\frac{D}{W}\Bigg)

''T''는 동작을 완료하는 평균 시간이다. (전통적으로 이 분야의 연구자는 이동 시간(movement time)을 의미하는 ''MT''를 사용한다)
''a''는 장치의 시작・정지 시간을 나타내고, ''b''는 장치 자체의 속도이다. 이들은 계측 데이터의 직선 근사에 의해 구해진다.
''D''는 시작점에서 대상의 중심까지의 거리이다 (전통적으로 이 분야의 연구자는 움직임의 폭 amplitude를 의미하는 ''A''를 사용한다)
''W''는 움직임의 방향으로 측정한 대상의 폭이다. ''W''는 동작의 최종 지점이 대상의 중심에서 ± 내에 있어야 하므로, 최종적인 위치에 대해 허용되는 오차로 생각할 수 있다.

위 식에서, 목표가 멀리 있거나 작을 경우 더 많은 시간이 걸리는 "속도와 정확성"의 트레이드 오프를 볼 수 있다.^[1]

피츠의 법칙의 대수 항은 목표 달성의 어려움 ''ID'' 라고 불리며, 단위는 비트이다. 이 법칙은 다음과 같이 표현할 수도 있다.

:

T = a + b ID,\,

여기서

:

ID = \log_2 \left(\frac{D}{W}+1\right)

이다. 즉, ''b'' 의 단위는 비트당 시간, 예를 들어 밀리초/비트이다. 상수 ''a''는 반응 시간, 또는 마우스를 클릭하는 데 필요한 시간을 포함하는 것으로 생각할 수 있다.

''a'' 와 ''b'' 는, 목표 지점을 가리키는 동작의 조건이 변화하면 변한다. 예를 들어 마우스와 스타일러스는 모두 목표 지점을 가리키는 데 사용되지만, ''a''와 ''b''는 각각 다르다.

성능 평가값 ''IP'' (처리율 ''TP'' 라고도 불린다)는, 차원이 단위 시간당 비트이며, 동작이 얼마나 빨리 완료될 수 있는지를 나타낸다. 특정 목표와는 무관하다.

''IP'' 의 정의에는 관례적으로 두 가지 방법이 있으며, ''IP'' = 1/''b'' 로 하거나 (이 경우, ''a'' 의 영향을 무시해 버린다), ''IP'' = ''ID''_average/''MT''_average 로 한다 (이 경우, 산출에 사용된 평균적인 ''ID''에 의존해 버린다).^[1] 어떤 정의가 사용되더라도, 다른 입력 장치에서 ''IP'' 를 측정함으로써, 각 장치의 목표 지점을 가리키는 동작에 대한 성능을 비교할 수 있다.

피츠의 원래 공식화는 샤논의 공식화와는 약간 달라서,

:

ID = \log_2 \left(\frac{2D}{W}\right)

였다. 여기서의 2는 특히 중요하지 않으며, ''ID'' 는 2를 고려하여 상수 ''a''、''b''를 변경하면 흡수할 수 있다. 샤논의 형식에서의 "+1"은, 특히 ''D''/''W''가 작은 경우에는, 피츠의 원래 식에 큰 영향을 주지 않는다.

샤논의 형식에는, ''ID''가 항상 음수가 아닌 것, 계측 결과에 더 잘 부합한다는 장점이 있다.^[1]

3. 모델의 발전

폴 모리스 피츠는 1954년 논문에서 대상 선택 작업의 난이도를 정량화하기 위한 지표를 제안했다.^[1] 이 지표는 정보 유사성을 기반으로, 대상 중심까지의 거리(''D'')를 신호로, 대상의 허용 오차 또는 너비(''W'')를 노이즈로 간주한다.

피츠가 제시한 ''난이도 지수''(ID, 비트 단위)는 다음과 같다.

: $\text{ID} = \log_2 \Bigg(\frac{2D} {W}\Bigg)$

피츠는 또한 인간의 수행 능력을 측정하기 위해 ''수행 지수''(IP, 초당 비트 단위)를 제안했는데, 이는 작업 난이도 지수(''ID'')와 대상 선택에 걸리는 이동 시간(''MT'', 초 단위)을 결합한 것이다. 피츠에 따르면, "일련의 동작에 의해 생성된 평균 정보량은 동작당 평균 정보량을 동작당 시간으로 나눈 값이다."^[1]

: $\text{IP} = \Bigg(\frac{\text{ID}} {\text{MT}}\Bigg)$

오늘날 ''IP''는 ''처리량''(TP)이라고 더 일반적으로 불린다. 정확성을 계산에 포함하는 것도 일반적이다.

이후 연구자들은 ''MT''와 ''D'' 및 ''W'' 작업 매개변수 간의 관계를 나타내는 선형 회귀 방정식을 구축하고 적합도를 위해 상관관계(''r'')를 검토했다.

: $\text{MT} = a + b \cdot \text{ID} = a + b \cdot \log_2 \Bigg(\frac{2D}{W}\Bigg)$

여기서:

''MT''는 동작 완료에 걸리는 평균 시간이다.
''a''와 ''b''는 입력 장치 선택에 따라 달라지는 상수로, 회귀 분석으로 결정된다. ''a''는 ''y''축 교차점으로 지연, ''b''는 기울기로 가속도를 설명한다. 두 매개변수는 피츠의 법칙에서 선형 종속성을 보인다.^[10]
''ID''는 난이도 지수이다.
''D''는 시작점에서 대상 중심까지의 거리이다.
''W''는 동작 축을 따라 측정한 대상 너비이다. 최종 동작 지점이 대상 중심에서 ± 이내여야 하므로, ''W''는 허용된 최종 위치 오차로도 간주된다.

''b'' 값은 컴퓨터 포인팅 장치 비교 지표로 사용될 수 있다. Card, English, Burr는 수행 지수(''IP''), 즉 를 사용해 다양한 입력 장치 성능을 비교, 마우스가 조이스틱이나 방향 이동 키보다 우수함을 보였다.^[11] 스튜어트 카드 자서전에 따르면, 이 연구는 "마우스가 제록스에 의해 상업적으로 도입되는 데 주요 요인"이었다.^[12]

많은 실험에서 거리나 너비 중 하나만 변경하면 모델 예측 능력이 저하된다.^[13]

피츠의 법칙은 시선 추적에 적용될 수 있다고 언급되지만, Drewes는 논란의 여지가 있다고 지적했다.^[14]

1956년 크로스먼은 목표 너비(''W'')를 유효 목표 너비(''W''_e)로 대체하는 개선을 제안했고, 피츠는 1964년 페터슨과 함께 발표한 논문에서 이를 사용했다.^[19]^[20]

''W''_e는 특정 ''D-W'' 조건에서 시행들의 선택 좌표 표준 편차로부터 계산된다. 선택이 목표 접근 축을 따라 ''x'' 좌표로 기록될 때,

:

W_e = 4.133 \times SD_x

따라서

:

\text{ID}_e = \log_2 \Bigg(\frac{D}{W_e}+1\Bigg)

그리고

:

\text{IP} = \Bigg(\frac{ID_e} {MT}}\Bigg)

선택 좌표가 정규 분포를 따르면, ''W''_e는 분포의 96%를 포함한다. ''W''_e를 사용하면, 피츠의 법칙 모델은 사용자의 실제 수행을 더 정확히 반영한다. ''IP'' 계산에 공간적 변동성, 즉 정확성이 포함된다.

3. 1. Welford의 모델

피츠의 법칙 과제 동안의 움직임은 다음 두 단계로 나눌 수 있다.^[10]

'''초기 움직임''': 목표 지점을 향한 빠르지만 부정확한 움직임
'''최종 움직임''': 목표를 획득하기 위한 느리지만 더 정확한 움직임

첫 번째 단계는 목표 지점까지의 거리에 의해 정의된다. 이 단계에서는 부정확하더라도 거리를 빠르게 좁힐 수 있다. 두 번째 움직임은 실제로 목표를 맞추기 위해 느리고 제어된 정밀한 움직임을 수행하려고 한다. 작업 시간은 난이도에 따라 선형적으로 증가한다.^[10] 그러나 서로 다른 작업이 동일한 난이도를 가질 수 있으므로, 목표 크기보다 거리가 전체 작업 완료 시간에 더 큰 영향을 미치는 것으로 파생된다.

원래 모델이 제안된 지 얼마 지나지 않아, 목표 거리와 너비가 이동 시간에 별개의 영향을 미친다는 직관에 따라 2요인 변형이 제안되었다. 1968년에 제안된 Welford의 모델은 목표 거리와 너비의 영향을 별도의 항으로 분리하여 예측력을 향상시켰다.^[19]

:

MT = a + b_1 \log_2 (D) + b_2 \log_2 (W)

이 모델은 추가 매개변수를 가지고 있어, 예측 정확도를 Fitts의 법칙의 1요인 형태와 직접 비교할 수 없다. 하지만, Shannon 공식을 참고하여 Welford의 모델을 변형한 식은 다음과 같다.

:

MT = a + b_1 \log_2 (D+W) + b_2 \log_2 (W) = a + b\log_2 \left(\frac{D+W}{W^k}\right)

추가 매개변수 ''k''를 통해 각도를 모델에 도입할 수 있다. 이제 사용자의 위치를 고려할 수 있다. 각도의 영향은 지수를 사용하여 가중치를 부여할 수 있다. 이러한 추가는 2010년에 Kopper 등이 도입했다.^[21]

이 공식은 ''k = 1''일 때 Shannon 형태로 축소된다. 따라서, 이 모델은 중첩 모델의 F-검정을 사용하여 Fitts의 법칙의 Shannon 형태와 직접 비교할 수 있다.^[22] 이 비교 결과, Welford의 Shannon 형태 모델이 이동 시간을 더 잘 예측할 뿐만 아니라, 제어-디스플레이 이득(예: 손 움직임과 커서 움직임의 비율)이 변경될 때도 더욱 강력하다는 것을 알 수 있다. 따라서, Shannon 모델이 약간 더 복잡하고 직관적이지 않지만, 가상 포인팅 작업에 사용하기에 경험적으로 가장 좋은 모델이다.

3. 2. 2차원 모델

피츠의 법칙은 원래 1차원 작업에만 적용되도록 설계되었다. 그러나 초기 실험에서는 피험자들이 상호 왕복 두드리기 작업이라고 불리는 테이블 위의 두 금속 판 사이에서 스타일러스(3차원)를 움직여야 했다.^[1] 움직임 방향에 수직인 대상 너비는 성능에 큰 영향을 미치지 않도록 매우 넓게 설정되었다. 피츠의 법칙의 주요 적용 분야는 컴퓨터 화면에서 2차원 가상 포인팅 작업으로, 대상은 두 차원에서 크기가 제한된다.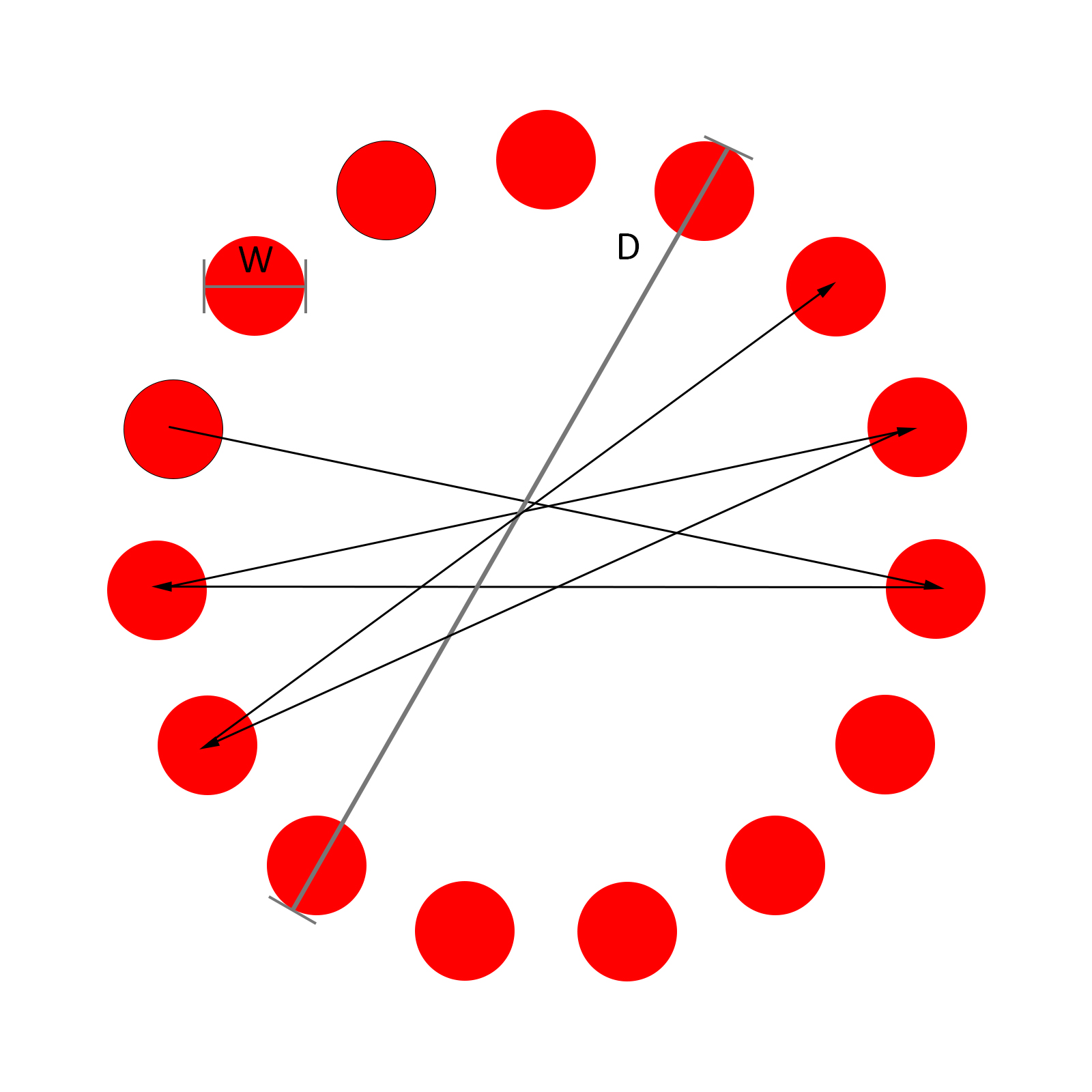

피츠의 법칙은 두 가지 다른 방식으로 2차원 작업으로 확장되었다. 예를 들어 계층적 풀다운 메뉴 탐색의 경우, 사용자는 메뉴 지오메트리에 의해 제한되는 포인팅 장치로 궤적을 생성해야 하며, 이 응용 프로그램에 대해 Accot-Zhai 조향 법칙이 파생되었다.

2차원 공간에서 대상을 가리키는 경우, 모델은 일반적으로 있는 그대로 유지되지만, 대상 지오메트리를 캡처하고 논리적으로 일관된 방식으로 목표 오류를 정량화하기 위해 조정이 필요하다.^[23]^[24] 대상 크기를 결정하기 위해 사용된 여러 가지 방법은 다음과 같다.^[25]

방법	설명
현상 유지	대상의 가로 너비
합 모델	W는 높이 + 너비와 같다.
면적 모델	W는 높이 * 너비와 같다.
더 작은 모델	W는 높이와 너비 중 더 작은 값이다.
W-모델	W는 움직임 방향의 유효 너비이다.

''W'' 모델이 때때로 최첨단 측정으로 간주되지만, 원형이 아닌 대상에 대한 진정으로 정확한 표현은 포인팅 장치의 궤적과 대상 간의 각도별 컨볼루션을 계산해야 하므로 훨씬 더 복잡하다.^[26]

4. UI 디자인에의 시사점

피츠의 법칙을 통해 다양한 GUI 디자인 가이드라인을 도출할 수 있다. 기본적으로 사용자가 클릭해야 하는 대상은 가능한 한 커야 한다. 이는 ''W'' 매개변수에서 파생된 것이다. 버튼의 유효 크기는 가능한 한 커야 하며, 사용자가 대상을 향해 움직이는 방향에 맞춰 형태를 최적화해야 한다.^[30]

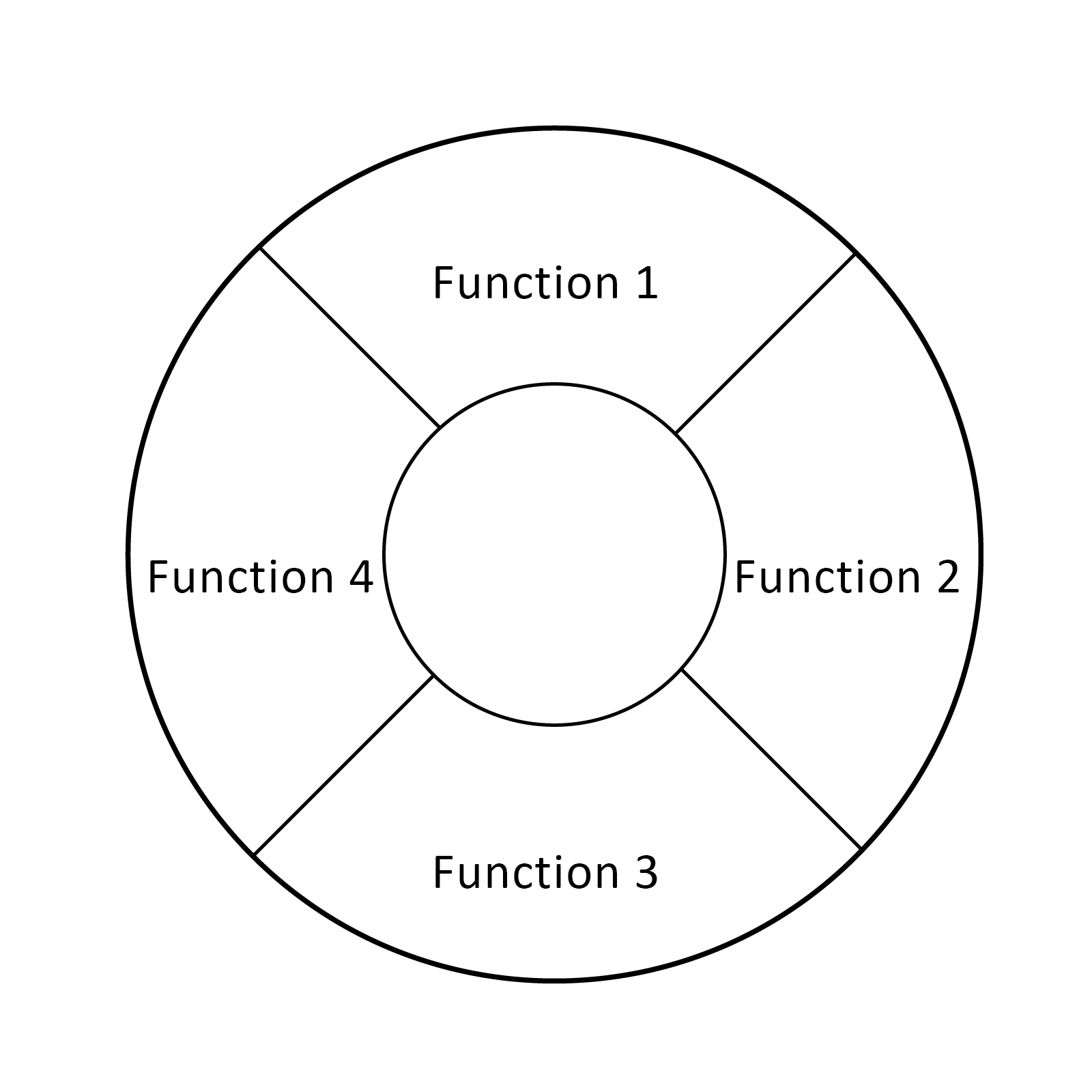
자주 함께 사용되는 기능들은 서로 묶어서 배치해야 한다. 이렇게 하면 ''D'' 매개변수를 최적화하여 이동 시간을 줄일 수 있다.^[30]

화면의 네 모서리에 요소를 배치하면 한 차원에서 무한히 큰 대상을 얻을 수 있어 이상적이다. 포인터는 항상 가장자리에 멈추기 때문에 사용자는 최대한의 속도로 마우스를 움직여도 대상을 클릭할 수 있다. 대상 영역은 이동 축을 따라 효과적으로 무한히 길어진다. 이 규칙은 "무한 모서리의 규칙"이라고 불린다. macOS는 현재 프로그램의 창 프레임 대신 항상 화면의 왼쪽 상단 가장자리에 메뉴 표시줄을 배치한다.^[30]

이 효과는 화면의 네 모서리에서 더 커진다. 두 모서리가 충돌하여 이론적으로 무한히 큰 버튼을 형성한다. 마이크로소프트 윈도우 (윈도우 11 이전 버전)는 "시작" 버튼을 왼쪽 하단 모서리에, 마이크로소프트 오피스 2007은 "오피스" 메뉴에 왼쪽 상단 모서리를 사용한다. 이 네 지점을 "매직 코너"라고 부른다.^[31] macOS는 프로그램 창의 왼쪽 상단에 닫기 버튼을 배치하고 메뉴 표시줄은 다른 버튼으로 매직 코너를 채운다.

고정된 드롭다운 메뉴 대신 팝업 메뉴를 사용하면 ''D'' 매개변수의 이동 시간을 줄일 수 있다. 사용자는 현재 마우스 위치에서 바로 상호 작용을 계속할 수 있으며 다른 영역으로 이동할 필요가 없다. 많은 운영 체제는 오른쪽 클릭 컨텍스트 메뉴를 표시할 때 이를 사용한다. 메뉴가 사용자가 클릭한 픽셀에서 바로 시작되므로 이 픽셀을 "매직" 또는 "프라임 픽셀"이라고 한다.^[25]

James Boritz 외 (1991)는 래디얼 메뉴 디자인을 비교했다.^[32] 래디얼 메뉴에서는 모든 항목이 프라임 픽셀에서 같은 거리에 있다. 이 연구는 실제 구현에서 사용자가 마우스를 움직여야 하는 방향도 고려해야 함을 보여준다. 오른손잡이 사용자의 경우 왼쪽 메뉴 항목을 선택하는 것이 오른쪽 메뉴 항목을 선택하는 것보다 훨씬 어려웠다. 상단에서 하단으로, 또는 그 반대로의 전환에서는 차이가 없었다.

일반적으로 사용자 인터페이스 설계에 다음과 같은 시사점을 준다.

버튼 등의 GUI 부품은 어느 정도 크기가 있어야 한다. 작으면 클릭이 어려워진다.
디스플레이의 모서리나 가장자리에 있는 요소 ( 윈도우 XP 'Luna' 테마의 "시작 버튼"이나, Mac OS X의 Apple & Spotlight 메뉴)는, 더 이상 마우스를 움직여도 화면의 가장자리이기 때문에 커서가 움직이지 않는 위치에 있으므로, 무한한 폭을 가지고 있는 것이 된다. 이 때문에 매우 조작하기 쉽다.
팝업 메뉴는 사용자가 마우스를 이동시킬 필요가 없으므로, 풀다운 메뉴보다 빠르게 열 수 있다.
파이형으로 배치된 메뉴의 요소는 직선으로 배치된 메뉴의 요소보다 빠르고, 실수가 적게 선택할 수 있다. 파이 메뉴는 중심으로부터의 거리가 모두 같고 짧은 위치에 놓이며, 선택하는 쐐기형 영역은 매우 크기 때문에(보통 화면의 가장자리까지 확대), 그렇다.

5. 비판 및 한계

피츠의 법칙은 다양한 조건에서 적용 가능하며 높은 정확도를 보이지만, 몇 가지 비판과 한계점도 가지고 있다.

섀넌 공식은 요크 대학교의 스콧 매켄지 교수가 제안한 것으로, 섀넌-하틀리 정리와 유사하여 널리 사용된다.^[15]^[16] 그러나 키보드 입력과 같은 작업에서는 섀넌 엔트로피가 피츠의 법칙과 다른 정보 값을 생성하여 오차가 발생할 수 있다.^[18] 이러한 오차는 일반적으로 무시할 수 있지만, 정보 처리 능력을 측정하는 경우에는 고려해야 한다.

''a''와 ''b'' 매개변수는 인터페이스 성능 지표 역할을 할 수 있지만, 사용자 간 변동과 인터페이스 간 변동을 분리해야 한다.^[18] 매개변수 식별 방법은 논쟁의 대상이며, 방법의 변동이 성능 차이를 압도할 수 있다.^[27]^[28] 또한, 성공률을 통합하는 문제도 있는데, 공격적인 사용자는 목표물을 놓치는 대가로 더 짧은 이동 시간을 달성할 수 있기 때문이다.

피츠의 법칙은 공간적으로 정의된 대상에만 적용되며, 시간적 대상에는 적용되지 않는다. 시간적 대상은 깜빡이는 대상이나 선택 영역으로 이동하는 대상과 같이 시간 축에서 정의되는 대상이다.^[29] 시간적 포인팅 모델은 2016년에 제시되었으며, 시간적 난이도 지수의 함수로서 오류율을 예측한다.^[29]

피츠의 법칙은 원래 1차원 동작에만 적용되었지만, 에이콧 차이의 법칙에 의해 2차원 동작에도 확장되었다. 또한, 단순 운동 반응만을 설명하며, 소프트웨어에 의한 커서 가속이나 훈련된 동작은 고려하지 않는다.

그럼에도 불구하고, 피츠의 법칙은 사용자 인터페이스 설계에 다음과 같은 시사점을 제공한다.

버튼과 같은 GUI 부품은 적절한 크기를 가져야 한다.
디스플레이 모서리나 가장자리에 있는 요소는 조작하기 쉽다.
팝업 메뉴는 풀다운 메뉴보다 빠르게 열 수 있다.
파이형 메뉴는 직선형 메뉴보다 빠르고 정확하게 선택할 수 있다.

참조

_[1] 논문 The information capacity of the human motor system in controlling the amplitude of movement 1954-06-01
_[2] 논문 A comparison of hand and foot movement times 1991-01-01
_[3] 논문 Human–computer interface controlled by the lip 2015-01-01
_[4] 논문 Effects of target movement direction cue on head-tracking performance 2000-01-01
_[5] 서적 Proceedings of the SIGCHI Conference on Human Factors in Computing Systems - CHI '91 1991-01-01
_[6] 논문 Movement time in an underwater environment 1973-01-01
_[7] 논문 Effects of age and sex on speed and accuracy of hand movements: And the refinements they suggest for Fitts's law
_[8] 논문 Fine motor deficiencies in children with developmental coordination disorder and learning disabilities: An underlying open-loop control deficit
_[9] 논문 Effects of marijuana on human reaction time and motor control
_[10] 논문 Physical versus virtual pointing 1996-01-01
_[11] 논문 Evaluation of mouse, rate-controlled isometric joystick, step keys, and text keys for text selection on a CRT http://bitsavers.tra[...] 1978-01-01
_[12] 웹사이트 Stuart Card http://www2.parc.com[...]
_[13] 간행물 Pointing on a Computer Display Simon Fraser University
_[14] 서적 Eye Gaze Tracking for Human Computer Interaction LMU München: Fakultät für Mathematik, Informatik und Statistik
_[15] 웹사이트 Scott MacKenzie's home page http://www.yorku.ca/[...]
_[16] 논문 Fitts' law as a research and design tool in human–computer interaction http://www.yorku.ca/[...] 1992-01-01
_[17] 서적 Extended Abstracts of the 2023 CHI Conference on Human Factors in Computing Systems ACM 2023-04-19
_[18] 논문 The Entropy of a Rapid Aimed Movement: Fitts' Index of Difficulty versus Shannon's Entropy
_[19] 서적 Fundamentals of Skill Methuen 1968-01-01
_[20] 논문 Information capacity of discrete motor responses 1964-01-01
_[21] 논문 A human motor behavior model for distal pointing tasks
_[22] 논문 Two-Part Models Capture the Impact of Gain on Pointing Performance 2012-12-01
_[23] 서적 Proceedings of the SIGCHI Conference on Human Factors in Computing Systems 2011-01-01
_[24] 서적 Proceedings of the SIGCHI conference on Human factors in computing systems - CHI '92 http://www.yorku.ca/[...] 1992-01-01
_[25] 논문 Fitt's Law: Modeling Movement Time in HCI
_[26] 논문 A probabilistic approach to modeling two-dimensional pointing. https://doi.org/10.1[...] 2005-09-01
_[27] 논문 Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts' law research in HCI https://web.archive.[...]
_[28] 간행물 On the Validity of Throughput as a Characteristic of Computer Input http://www.m.shuminz[...] 2002-01-01
_[29] 서적 Proceedings of the 2016 CHI Conference on Human Factors in Computing Systems ACM 2016-01-01
_[30] 웹사이트 Visualizing Fitts's Law http://www.particlet[...] Particletree 2019-12-08
_[31] 웹사이트 Giving You Fitts https://blogs.msdn.m[...] Microsoft Developer 2019-12-08
_[32] 논문 Fitts's law studies of directional mouse movement
_[33] 문서 http://www.bcs-hci.o[...]

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com