결정론적 유한 상태 기계

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 형식적 정의
- 2.1. 작동 방식
3. 예제
4. 변형
5. 폐포 성질
6. 전이 모노이드
7. 장점과 단점
- 7.1. 장점
- 7.2. 단점
8. DFA 식별
9. 동등한 모델
- 9.1. 읽기 전용 우측 이동 튜링 기계
10. 비순환 결정적 유한 오토마톤 (ADFA)
참조

1. 개요

결정적 유한 상태 기계(DFA)는 5-튜플로 정의되며, 유한한 상태 집합, 입력 기호, 전이 함수, 시작 상태, 수락 상태 집합으로 구성된다. DFA는 문자열을 입력으로 받아들이거나 거부하며, 수락하는 문자열 집합은 DFA가 인식하는 언어가 된다. DFA는 완전, 불완전, 지역 오토마톤 등 다양한 변형이 존재하며, 무작위 DFA의 특성도 연구된다.

DFA는 합집합, 교집합, 보수, 결합, 클레이니 스타 등의 연산에 대해 닫혀 있으며, 전이 함수는 전이 모노이드를 형성한다. DFA는 시뮬레이션이 용이하고 효율적인 알고리즘을 제공하는 장점이 있지만, 괄호 언어와 같이 복잡한 언어를 인식하는 데 한계가 있다. DFA 식별 문제는 주어진 긍정적 및 부정적 단어 집합을 기반으로 DFA를 구성하는 문제로, 최소 상태 DFA를 찾는 것은 NP-완전 문제이다. DFA는 읽기 전용 우측 이동 튜링 기계와 동등하며, 비순환 DFA(ADFA)는 빠른 검색을 위한 데이터 구조로 사용된다.

2. 형식적 정의

결정적 유한 오토마톤 ''M''은 5개의 요소로 구성된 튜플 (''Q'', Σ, ''δ'', ''q''₀, ''F'')로 정의되며, 각 요소는 다음과 같다.

''Q'': 상태들의 유한 집합
Σ: 입력 기호들의 유한 집합. 이를 알파벳이라고 한다.
''δ'': 전이 함수. ''Q'' × Σ → ''Q'' 형태의 함수이다.
''q''₀: 시작 상태. ''Q''에 속하는 원소이다 (''q''₀ ∈ ''Q'').
''F'': 수락 상태들의 집합. ''Q''의 부분 집합이다 (''F'' ⊆ ''Q'').

알파벳 Σ에 속한 문자들로 이루어진 문자열 ''w'' = ''a''₁''a''₂...''a_n''가 주어졌을 때, 오토마톤 ''M''은 다음 세 조건을 만족하는 상태들의 순서 ''r''₀, ''r''₁, ..., ''r_n''이 ''Q'' 안에 존재할 경우 문자열 ''w''를 '''수락한다'''.

# ''r''₀ = ''q''₀

# ''r''_''i''+1 = ''δ''(''r_i'', ''a''_''i''+1) (단, ''i'' = 0, ..., ''n'' − 1)

# ''r_n'' ∈ ''F''

간단히 말해, 기계는 시작 상태 ''q''₀에서 출발하여(조건 1), 입력 문자열 ''w''의 각 문자를 순서대로 읽으면서 전이 함수 ''δ''에 따라 상태를 바꿔나간다(조건 2). 문자열 전체를 다 읽었을 때 도달한 최종 상태 ''r_n''이 수락 상태 집합 ''F''에 포함되면(조건 3), 기계는 문자열 ''w''를 수락한다. 그렇지 않으면 문자열을 '''거부한다'''.

오토마톤 ''M''이 수락하는 모든 문자열의 집합을 ''M''이 '''인식하는''' 형식 언어라고 하며, ''L''(''M'')으로 표기한다.

수락 상태 집합 ''F''와 시작 상태 ''q''₀가 정의되지 않은 결정적 유한 오토마톤은 전이 시스템 또는 반자동 기계라고 부른다.

더 자세한 형식적 정의는 오토마타 이론 문서에서 찾아볼 수 있다.

2. 1. 작동 방식

결정론적 유한 상태 기계(DFA)는 입력된 문자열을 처리하여 특정 패턴이나 규칙에 맞는지 검사하는 추상적인 기계이다. DFA는 다음의 다섯 가지 요소로 정의된다.

상태 집합 (''Q''): 기계가 가질 수 있는 모든 상태들의 유한 집합.
문자 집합 (Σ): 기계가 입력으로 받을 수 있는 모든 문자들의 유한 집합. 입력 알파벳이라고도 한다.
전이 함수 (δ): 현재 상태와 입력 문자를 받아 다음 상태를 결정하는 함수. 형식적으로는 ''Q'' × Σ → ''Q'' 로 표현된다. 즉, (현재 상태, 입력 문자) 쌍을 입력받아 다음 상태 하나를 출력한다.
시작 상태 (''q''₀): 기계가 작동을 시작하는 초기 상태. 상태 집합 ''Q''의 원소 중 하나이다 (''q''₀ ∈ ''Q'').
수락 상태 집합 (''F''): 기계가 입력을 성공적으로 처리했다고 판단하는 상태들의 집합. 상태 집합 ''Q''의 부분 집합이다 (''F'' ⊆ ''Q'').

DFA의 작동 방식은 다음과 같다. 먼저, 기계는 지정된 시작 상태 (''q''₀)에서 출발한다. 그 다음, 입력 문자열(예: ''a = a₀a₁ ... a_n−1'')을 처음부터 끝까지 한 문자씩 순서대로 읽어들인다. 각 문자를 읽을 때마다 전이 함수 (δ)를 사용하여 현재 상태에서 다음 상태로 이동한다. 구체적으로, 현재 상태가 ''q_i''이고 읽어들인 문자가 ''a_i''일 때, 다음 상태 ''q_i+1''는 δ(''q_i'', ''a_i'')로 결정된다.

이 과정을 입력 문자열의 마지막 문자까지 반복한다. 문자열 전체를 다 처리했을 때 도달한 최종 상태(위 예시에서는 ''q_n'')가 수락 상태 집합 (''F'')에 포함되어 있으면, DFA는 해당 입력 문자열을 '''수락한다'''고 판단한다. 만약 최종 상태가 수락 상태 집합에 포함되지 않으면, 문자열을 '거부'한다.

결국, DFA는 주어진 형식 언어에 속하는 문자열들만을 선별하여 수락하는 역할을 한다. DFA가 수락하는 모든 문자열의 집합이 바로 그 DFA가 인식하는 언어이다.

3. 예제

다음은 이진 알파벳을 사용하며 입력 문자열에 포함된 '0'의 개수가 짝수인 경우에만 이를 인식하는 결정론적 유한 상태 기계(DFA) ''A''의 예시이다.

''A'' = (''Q'', ''Σ'', ''δ'', ''q''₀, ''F'') 로 정의되며, 각 구성 요소는 다음과 같다.

상태 집합 ''Q'' = {''q''₀, ''q''₁}
입력 알파벳 ''Σ'' = {0, 1}
시작 상태 ''q''₀
수용 상태 집합 ''F'' = {''q''₀}
전이 함수 ''δ''는 다음 상태 전이 표와 같이 정의된다.

전이 함수 ''δ''의 상태 전이표
상태	입력 0	입력 1
q₀	q₁	q₀
q₁	q₀	q₁

''A''의 상태 다이어그램은 다음과 같다.

상태 ''q''₀는 지금까지 입력된 문자열에 포함된 '0'의 개수가 짝수임을 나타내고, 상태 ''q''₁는 홀수임을 나타낸다. 입력으로 '1'이 들어오는 경우에는 오토마톤의 상태가 변하지 않는다. 입력 문자열 처리가 모두 끝났을 때, 현재 상태가 ''q''₀이면 입력된 '0'의 개수가 짝수라는 의미이므로, 해당 문자열은 ''A''에 의해 인식(수용)된다.

''A''가 인식하는 언어는 정규 언어이며, 다음 정규 표현식으로 나타낼 수 있다. 여기서 `*`는 클레이니 스타 연산을 의미한다.

: $1^*(01^*01^*)^* \,\!$

4. 변형

결정론적 유한 상태 기계(DFA)는 기본적인 정의 외에도 여러 가지 변형된 형태가 존재한다. 일반적인 DFA는 모든 상태에서 모든 입력 기호에 대한 전이가 정의된 완전(complete)한 형태이지만, 일부 전이가 정의되지 않은 불완전(incomplete)한 형태도 고려될 수 있다. 또한, 특정 제약 조건을 만족하는 DFA의 한 종류인 '''지역 오토마톤'''은 지역 언어를 인식하는 데 사용된다. 더 나아가 DFA를 유향 그래프로 간주하고 무작위성을 도입하여 그 구조적 특성, 예를 들어 강결합 컴포넌트의 크기 등을 분석하는 연구도 이루어지고 있다. 이러한 다양한 변형 모델들은 DFA의 이론적 탐구나 특정 응용 분야에서의 활용 가능성을 넓혀준다.

4. 1. 완전 및 불완전 DFA

일반적인 정의에 따르면, 결정론적 유한 상태 기계(DFA)는 완전(complete)하다. 이는 모든 상태에서 모든 가능한 입력 기호에 대해 다음 상태로의 전이가 반드시 정의되어 있다는 의미이다.

하지만 일부 저자들은 결정론적 유한 상태 기계를 약간 다르게 정의하기도 한다. 이 정의에 따르면, 각 상태와 각 입력 기호에 대해 전이가 최대 하나만 존재할 수 있다. 즉, 전이 함수가 부분 함수일 수 있다는 것이다.^[2] 만약 특정 상태에서 특정 입력 기호에 대한 전이가 정의되어 있지 않다면, 해당 자동 장치는 그 시점에서 작동을 멈춘다.

4. 2. 지역 오토마타

'''지역 오토마톤'''은 반드시 모든 상태에서 모든 입력 기호에 대한 전이가 정의될 필요는 없는 DFA의 한 종류이다. 지역 오토마톤의 중요한 특징은 동일한 기호(레이블)가 붙은 모든 간선은 반드시 하나의 특정 정점으로만 향해야 한다는 점이다. 지역 오토마톤은 지역 언어라고 불리는 언어들을 인식한다. 지역 언어는 어떤 단어가 해당 언어에 속하는지 여부를 그 단어 내에서 연속된 두 개의 기호(길이가 2인 "슬라이딩 윈도우")만 보고 판단할 수 있는 언어를 말한다.

'''마이힐 그래프'''는 주어진 알파벳 ''A''에 대한 유향 그래프이다. 이 그래프의 정점 집합은 알파벳 ''A''의 기호들로 이루어지며, 정점들 중 일부는 "시작 정점"으로, 또 다른 일부는 "종료 정점"으로 지정된다. 마이힐 그래프가 인식하는 언어는 시작 정점에서 출발하여 종료 정점에서 끝나는 모든 유향 경로들의 집합이다. 즉, 마이힐 그래프 자체가 일종의 오토마톤처럼 작동하는 것이다. 마이힐 그래프가 인식할 수 있는 언어들의 부류는 정확히 지역 언어들의 부류와 일치한다.

4. 3. 무작위성

시작 상태와 수락 상태를 무시하면, ''n''개의 상태와 크기 ''k''의 알파벳을 가진 DFA는 모든 정점이 1부터 ''k''까지 표시된 ''k''개의 나가는 간선을 갖는 ''n''개의 정점을 가진 유향 그래프로 볼 수 있다 (''k''-아웃 유향 그래프). ''k'' ≥ 2가 고정된 정수일 때, 이러한 ''k''-아웃 유향 그래프 중에서 무작위로 균일하게 선택된 가장 큰 강결합 컴포넌트 (SCC)는 높은 확률로 상태 개수 ''n''에 비례하는 크기를 가지며 모든 정점에서 도달할 수 있다는 것이 알려져 있다.^[3] 또한, ''k''가 ''n''이 증가함에 따라 함께 증가하도록 허용하면 전체 유향 그래프는 연결성에 대한 에르되시-레니 모형과 유사하게 강결합에 대한 위상 변환을 갖는다는 것이 증명되었다.^[4]

무작위 DFA에서, 한 정점에서 도달할 수 있는 최대 정점 수는 높은 확률로 가장 큰 SCC의 정점 수와 매우 가깝다.^[3]^[5] 이는 또한 최소 진입 차수가 1인 가장 큰 유도된 부분 유향 그래프에도 적용되며, 이는 1-코어의 유향 버전으로 볼 수 있다.^[4]

5. 폐포 성질

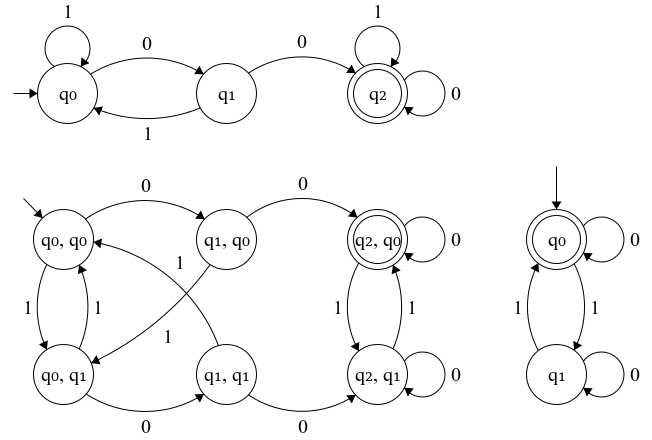
위쪽 왼쪽 오토마톤은 "00"이 한 번 이상 나타나는 모든 이진 문자열의 언어를 인식한다. 아래쪽 오른쪽 오토마톤은 1의 개수가 짝수인 모든 이진 문자열을 인식한다. 아래쪽 왼쪽 오토마톤은 앞의 두 오토마톤의 곱으로 얻어지며, 두 언어의 교집합을 인식한다.

만약 결정론적 유한 상태 기계(DFA)가 DFA로 인식 가능한 언어에 연산을 적용하여 얻은 언어를 인식한다면, DFA는 해당 연산에 대해 폐포되어 있다고 말한다. DFA는 다음 연산에 대해 폐포되어 있다.

합집합
교집합 (그림 참조)
결합
보수
클레이니 스타
역전^[6]
몫^[6]
대체^[7]
준동형 사상^[6]^[7]

각 연산에 대해 상태 수를 기준으로 최적의 구성이 상태 복잡도 연구에서 결정되었다.

DFA는 비결정적 유한 오토마타 (NFA)와 동치이므로, 이러한 폐포는 NFA의 폐포 속성을 사용하여 증명할 수도 있다.

6. 전이 모노이드

주어진 DFA의 실행 과정은 전이 함수를 자기 자신과 여러 번 합성하는 것으로 이해할 수 있다.

입력 알파벳 $\Sigma$ 에 속하는 각 기호 $a$ 에 대해, 상태 $q \in Q$ 를 입력받아 다음 상태 $\delta(q, a)$ 를 반환하는 새로운 함수 $\delta_a : Q \rightarrow Q$ 를 정의할 수 있다. 즉, 모든 $q \in Q$ 에 대해 $\delta_a(q) = \delta(q, a)$ 이다. 이는 여러 인수를 받는 함수를 하나의 인수를 받는 함수의 연속으로 표현하는 기법인 커링(Currying)을 이용한 것이다. 이렇게 정의된 함수 $\delta_a$ 는 상태 집합 $Q$ 에 "작용"하여 현재 상태를 다음 상태로 변화시키는 역할을 한다.

이제 여러 입력 기호에 대한 전이를 생각해보자. 예를 들어, 두 기호 $a, b \in \Sigma$ 가 순서대로 입력될 때의 상태 변화는 각 기호에 대한 함수 $\delta_a$ 와 $\delta_b$ 를 합성하여 나타낼 수 있다. 함수 합성을 $\circ$ 로 표기하면, 새로운 함수 $\widehat\delta_{ab} = \delta_b \circ \delta_a$ 를 정의할 수 있다. (함수 합성은 일반적으로 오른쪽에서 왼쪽으로 적용되므로, 문자열 "ab"에 대한 전이는 $\delta_b(\delta_a(q))$ 형태로 표현된다. 원본 소스에서는 $\widehat\delta_{ab}=\delta_a \circ \delta_b$ 로 표기하였으나, 이는 $\widehat\delta(q, wa) = \delta_a(\widehat\delta(q, w))$ 정의와 일관성을 맞추기 위한 표기로 이해할 수 있다. 즉, $\widehat\delta(q, ab) = \delta_b(\widehat\delta(q, a)) = \delta_b(\delta_a(\widehat\delta(q, \epsilon))) = \delta_b(\delta_a(q))$ 가 되며, 이는 $\delta_b \circ \delta_a$ 와 같다. 혼동을 피하기 위해 확장된 전이 함수 $\widehat\delta$ 정의를 사용하는 것이 좋다.)

이 과정을 일반화하여, 빈 문자열 $\epsilon$ 을 포함한 모든 문자열 $w \in \Sigma^{\star}$ 에 대한 전이 함수 $\widehat\delta : Q \times \Sigma^{\star} \rightarrow Q$ 를 재귀적으로 정의할 수 있다.

$\widehat\delta ( q, \epsilon ) = q$ (빈 문자열 $\epsilon$ 은 상태를 변화시키지 않는다)
$\widehat\delta ( q, wa ) = \delta_a(\widehat\delta ( q, w ))$ (문자열 $w$ 뒤에 기호 $a$ 가 오는 경우, 먼저 $w$ 에 대한 상태 전이를 계산하고, 그 결과 상태에 $a$ 에 대한 전이 함수 $\delta_a$ 를 적용한다. 여기서 $w \in \Sigma ^*, a \in \Sigma, q \in Q$ 이다.)

이렇게 정의된

\widehat\delta

는 DFA가 특정 입력 문자열을 처리했을 때의 최종 상태를 나타내며, DFA의 전체 실행은

\widehat\delta

함수의 반복적인 합성으로 볼 수 있다.

이러한 함수 합성 연산은 수학적인 구조인 모노이드(Monoid)를 형성한다. 상태 집합

Q

에서

Q

로 가는 함수들의 집합(

\{\widehat\delta_w | w \in \Sigma^* \}

, 여기서

\widehat\delta_w(q) = \widehat\delta(q, w)

)과 함수 합성 연산으로 구성된 이 모노이드를 해당 DFA의 전이 모노이드(transition monoid)라고 부른다. 때로는 변환 반군(transformation semigroup)이라고도 한다.

역으로, 전이 모노이드의 생성원(각

\delta_a

함수)들을 알면 원래의 전이 함수

\delta

를 복원할 수 있으므로, DFA를 정의하는 표준적인 방식(상태, 알파벳, 전이 함수, 시작 상태, 종료 상태 집합)과 전이 모노이드를 이용한 설명은 서로 동등하다.

7. 장점과 단점

결정론적 유한 상태 기계(DFA)는 계산 모델 중 매우 실용적인 모델 중 하나로 평가된다. 이는 입력을 처리하는 효율적인 온라인 알고리즘이 존재하고, 언어의 보수, 합집합, 교집합 연산이나 상태 최소화 등 다양한 문제에 대한 효율적인 알고리즘을 제공하기 때문이다.

비결정적 유한 오토마타(NFA)와 계산 능력은 동일하지만, 멱집합 구성을 통해 NFA를 DFA로 변환할 경우 상태 수가 기하급수적으로 증가할 수 있다는 점은 고려해야 한다.^[8]

반면, DFA는 인식할 수 있는 언어의 범위가 제한적이라는 명확한 한계를 가진다. 예를 들어, 괄호의 짝을 맞추는 딕 언어나 특정 문자가 동일한 횟수만큼 반복되는 언어와 같이 개수를 세어야 하는 구조의 언어는 DFA로 인식하기 어렵다.

7. 1. 장점

결정론적 유한 상태 기계(DFA)는 계산 모델 중 매우 실용적인 모델 중 하나로 평가된다. 그 이유는 입력 문자열에 대해 DFA를 시뮬레이션하는 간단한 온라인 알고리즘이 존재하며, 이 알고리즘은 선형 시간과 상수 공간만을 사용하여 효율적으로 작동하기 때문이다.

또한, DFA와 관련된 여러 가지 유용한 연산을 수행하는 효율적인 알고리즘들이 개발되어 있다. 예를 들어 다음과 같은 작업을 효율적으로 처리할 수 있다.

주어진 DFA가 인식하는 언어의 보수를 인식하는 새로운 DFA 찾기.
주어진 두 DFA가 인식하는 언어들의 합집합 또는 교집합을 인식하는 DFA 찾기.

DFA는 상태 수를 최소화한 ''표준 형식'', 즉 최소 DFA로 변환될 수 있다는 장점도 있다. 이러한 특징으로 다음과 같은 여러 중요한 결정 문제들을 효율적으로 해결하는 알고리즘을 사용할 수 있다.

비어있음 문제: DFA가 어떤 문자열이라도 받아들이는지 여부를 결정한다.
보편성 문제: DFA가 가능한 모든 문자열을 받아들이는지 여부를 결정한다.
동등성 문제: 두 개의 DFA가 정확히 동일한 언어를 인식하는지 여부를 결정한다.
포함 문제: 한 DFA가 인식하는 언어가 다른 DFA가 인식하는 언어에 완전히 포함되는지 여부를 결정한다.
최소화 문제: 특정 정규 언어를 인식하는 DFA 중에서 상태 수가 가장 적은 DFA를 찾는다.

비결정적 유한 오토마타(NFA)와 비교했을 때, DFA는 계산 능력 면에서는 동일하다. 모든 DFA는 그 자체로 NFA이며, 어떤 NFA라도 멱집합 구성이라는 방법을 통해 동일한 언어를 인식하는 DFA로 변환될 수 있다. 그러나 이 변환 과정에서 DFA의 상태 수가 NFA보다 기하급수적으로 많아질 가능성이 있다.

그럼에도 불구하고, 문제 해결의 효율성 측면에서는 DFA가 NFA보다 유리한 경우가 많다. 위에서 언급한 결정 문제들, 특히 보편성, 동등성, 포함, 최소화 문제는 NFA에 대해서는 PSPACE 완전 문제로 알려져 있어 효율적인 해결이 어렵다.^[8] 예를 들어, NFA가 모든 문자열을 인식하는지(보편성) 확인하는 것은 복잡할 수 있지만, DFA의 경우 모든 상태가 최종 상태인지 확인하는 것만으로 비교적 간단하게 판별할 수 있다. 이러한 효율성 덕분에 DFA는 다양한 실제 응용 분야에서 유용하게 활용된다.

7. 2. 단점

유한 상태 오토마타는 인식할 수 있는 언어의 범위가 엄격하게 제한된다는 단점이 있다. 예를 들어, 문제를 해결하는 데 상수 공간 이상이 필요한 많은 단순한 언어는 DFA로 인식할 수 없다.

DFA가 인식할 수 없는 간단한 언어의 대표적인 예는 괄호 또는 딕 언어이다. 이 언어는 "(()())"와 같이 괄호의 쌍이 올바르게 맞춰진 단어들로 이루어진다. 직관적으로 DFA는 딕 언어를 인식할 수 없는데, 이는 DFA가 개수를 세는 능력이 없기 때문이다. DFA와 유사한 오토마타는 현재 열려 있는 괄호의 모든 가능한 개수를 상태로 표현해야 하므로, 무한히 많은 상태가 필요하게 된다. 또 다른 간단한 예로는 어떤 유한하지만 임의의 개수의 'a' 뒤에 정확히 같은 개수의 'b'가 오는 언어(예: "aaabbb")가 있다.

또한, 비결정적 유한 오토마타 (NFA)를 DFA로 변환할 때, DFA의 상태 수가 NFA에 비해 기하급수적으로 많아질 수 있다.^[8] 비록 NFA와 DFA가 계산 능력은 동일하지만, 이러한 상태 수 증가는 실제 구현에서 문제가 될 수 있다.

8. DFA 식별

주어진 긍정적인 단어 집합 $S^+ \subset \Sigma^*$ 과 부정적인 단어 집합 $S^- \subset \Sigma^*$ 을 이용하여, $S^+$ 에 속하는 모든 단어는 받아들이고 $S^-$ 에 속하는 모든 단어는 거부하는 DFA를 만드는 문제가 있다. 이 문제를 DFA 식별 (DFA identification) 또는 DFA 합성, 학습이라고 부른다.

일부 특수한 경우에는 DFA를 선형 시간에 만들 수 있지만, 상태 개수가 가장 적은 최소 DFA를 찾는 문제는 NP-완전 문제로 알려져 있어 계산적으로 매우 어렵다.^[9]

최소 DFA 식별을 위한 최초의 알고리즘은 트락텐브로트(Trakhtenbrot)와 바르즈딘(Barzdin)이 제안한 TB-알고리즘이다.^[10] 하지만 이 알고리즘은 주어진 길이까지의 모든 가능한 단어가 $S^+ \cup S^-$ 안에 포함되어 있다고 가정하는 한계가 있다.

이후 K. 랑(K. Lang)은 이러한 가정이 필요 없는 TB-알고리즘의 확장판인 Traxbar 알고리즘을 제안했다.^[11] 그러나 Traxbar 알고리즘은 찾아낸 DFA가 반드시 최소 DFA임을 보장하지는 않는다. E. M. 골드(E. M. Gold) 역시 최소 DFA 식별을 위한 휴리스틱 알고리즘을 제안했다.^[9] 골드 알고리즘은 입력 데이터 $S^+$ 와 $S^-$ 가 해당 정규 언어의 특성 집합을 포함하고 있다고 가정한다. 만약 이 가정이 만족되지 않으면, 생성된 DFA는 주어진 데이터와 일치하지 않을 수 있다.

그 외 주목할 만한 DFA 식별 알고리즘으로는 RPNI 알고리즘,^[12] Blue-Fringe 증거 기반 상태 병합(evidence-driven state-merging) 알고리즘,^[13] 그리고 Windowed-EDSM^[14] 등이 있다.

또 다른 연구 흐름은 진화 알고리즘을 적용하는 것이다. 스마트 상태 레이블링 진화 알고리즘^[15]은 훈련 데이터( $S^+$ 와 $S^-$ )에 일부 단어가 잘못 분류된 '노이즈'가 포함된 경우에도 DFA 식별 문제를 해결할 수 있도록 개선되었다.

최근에는 SAT 솔버를 이용하는 방법도 개발되었다. 마르진 J. H. 헤울레(Marijn J. H. Heule)와 S. 베르워(S. Verwer)는 최소 DFA 식별 문제를 부울 공식의 만족 여부를 결정하는 문제로 변환했다.^[16] 이 방법의 핵심 아이디어는 입력 단어들을 기반으로 증강된 접두사 트리(트라이)를 만들고, 이 트리의 노드들을 $C$ 개의 색깔(상태)로 칠하는 문제를 푸는 것이다. 같은 색깔로 칠해진 노드들이 하나의 상태로 합쳐졌을 때, 결과로 만들어지는 오토마톤이 결정론적이고 주어진 $S^+$ 와 $S^-$ 를 올바르게 구분하도록 하는 색칠 방법을 찾는 것이다. 이 접근법은 최소 DFA를 찾을 수 있다는 장점이 있지만, 입력 데이터의 크기가 커지면 실행 시간이 기하급수적으로 증가하는 단점이 있다.

이러한 단점을 보완하기 위해, 헤울레와 베르워의 초기 알고리즘은 나중에 EDSM 알고리즘의 일부 단계를 먼저 수행하여 검색 공간을 줄인 후 SAT 솔버를 실행하는 방식으로 개선되었다. 이를 DFASAT 알고리즘이라고 한다.^[17] 이 방법은 실행 속도를 높일 수 있지만, 찾아낸 DFA가 최소임을 보장하지는 못한다. 검색 공간을 줄이는 또 다른 방법은 울리안체프(Ulyantsev) 등이 제안한 것으로,^[18] BFS 알고리즘에 기반한 새로운 대칭성 제거 기법을 사용한다. 이 기법은 찾아낼 DFA의 상태 번호를 초기 상태에서 시작하는 BFS 순서에 따라 매기도록 제한하여, 동형인 오토마타들을 탐색 과정에서 배제함으로써 검색 공간을 $C!$ 만큼 줄인다.

9. 동등한 모델

결정론적 유한 오토마타(DFA)는 계산 능력 측면에서 동일한 성능을 보이는 여러 다른 모델들과 비교될 수 있다. 이러한 모델들은 서로 다른 방식으로 정의되지만, 모두 동일한 종류의 언어, 즉 정규 언어를 인식할 수 있다. 대표적인 예시 중 하나로 읽기 전용 우측 이동 튜링 기계가 있으며, 이는 DFA와 거의 동일한 방식으로 작동한다.

9. 1. 읽기 전용 우측 이동 튜링 기계

'''읽기 전용 우측 이동 튜링 기계'''는 오직 오른쪽으로만 이동하는 특정 유형의 튜링 기계이며, 이는 DFA와 거의 정확히 동일하다.^[19]

단일 무한 테이프를 기반으로 하는 정의는 7-튜플이다.

:

M = \langle Q, \Gamma, b, \Sigma, \delta, q_0, F \rangle,

여기서

:

Q

는 유한한 ''상태'' 집합이다;

:

\Gamma

는 유한한 ''테이프 알파벳/기호'' 집합이다;

:

b \in \Gamma

는 ''공백 기호''이며 (계산 중 어느 단계에서든 테이프에 무한히 많이 나타날 수 있는 유일한 기호임);

:

\Sigma

는

\Gamma

의 부분 집합으로

b

를 포함하지 않으며, ''입력 기호'' 집합이다;

:

\delta: Q \times \Gamma \to Q \times \Gamma \times \{R\}

는 ''전이 함수''라고 불리는 함수이며, ''R''은 오른쪽 이동(오른쪽 시프트)이다;

:

q_0 \in Q

는 ''초기 상태''이다;

:

F \subseteq Q

는 ''최종 상태'' 또는 ''수용 상태''의 집합이다.

이 기계는 항상 정규 언어를 수용한다. 언어가 비어 있지 않으려면 집합 F ('''HALT''' 상태)의 요소가 하나 이상 존재해야 한다.

10. 비순환 결정적 유한 오토마톤 (ADFA)

비순환 결정적 유한 오토마톤(Acyclic Deterministic Finite Automaton^eng, ADFA)은 순환적인 상태 전이(transition)가 없는 결정론적 유한 상태 기계이다. 즉, 한 번 특정 상태를 떠나면 다시 그 상태로 돌아오는 경로가 존재하지 않는다. 이러한 특성 때문에 ADFA는 오직 유한한 길이의 문자열 집합만을 표현할 수 있다.

ADFA는 매우 빠른 검색 속도를 제공하여 단어를 저장하고 검색하는 자료 구조로 유용하게 사용된다. 특히, 최소화된 ADFA는 저장 공간을 매우 효율적으로 사용하며, 그 크기가 저장되는 키(단어)의 수에 반드시 비례하지는 않는다. 어떤 경우에는 저장하는 단어의 수가 늘어나도 데이터 구조 전체의 크기가 오히려 줄어들기도 하는데, 이는 저장되는 문자열들의 패턴과 복잡성에 따라 달라진다.

대표적인 예로, 문자열 검색에 흔히 사용되는 트라이는 ADFA의 한 종류로 간주할 수 있다.

참조

_[1] 간행물 Proceedings of the 27th International Conference on Program Comprehension, ICPC 2019, Montreal, QC, Canada, May 25-31, 2019 IEEE / ACM
_[2] 서적 Introduction to Compiler Design Springer
_[3] 논문 Limit distributions of certain characteristics of random automaton graphs 1973
_[4] 논문 The graph structure of a deterministic automaton chosen at random 2017-10
_[5] conference Distribution of the number of accessible states in a random deterministic automaton https://hal.archives[...] 2012-02
_[6] 논문 Closures which Preserve Finiteness in Families of Languages
_[7] 논문 Grammars and languages
_[8] 웹사이트 Operations and tests on sets: Implementation on DFAs https://www7.in.tum.[...] 2016-11-16
_[9] 논문 Complexity of Automaton Identification from Given Data
_[10] 서적 Finite Automata: Behavior and Synthesis https://books.google[...] Elsevier 2014-06-28
_[11] 서적 Proceedings of the fifth annual workshop on Computational learning theory - COLT '92
_[12] 서적 Pattern Recognition and Image Analysis
_[13] 서적 Grammatical Inference http://eprints.mayno[...]
_[14] 서적 Beyond EDSM {{pipe}} Proceedings of the 6th International Colloquium on Grammatical Inference: Algorithms and Applications https://dl.acm.org/d[...] Springer 2002-09-23
_[15] 논문 Learning deterministic finite automata with a smart state labeling evolutionary algorithm
_[16] conference Grammatical Inference: Theoretical Results and Applications 2010
_[17] 논문 Software model synthesis using satisfiability solvers https://lirias.kuleu[...]
_[18] 서적 Language and Automata Theory and Applications
_[19] 서적 Second Edition: Computability, Complexity, and Languages and Logic: Fundamentals of Theoretical Computer Science Academic Press, Harcourt, Brace & Company
_[20] 서적 コンパイラI 原理・技法・ツール、A.V.エイホ・R.セシィ、J.D.ウルマン共著、原田賢一訳、サイエンス社、134頁
_[21] 문서 Hopcroft 2001
_[22] 문서 McCulloch and Pitts (1943)
_[23] 문서 Rabin and Scott (1959)

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com