고유값 분해

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 고윳값과 고유 벡터
- 2.1. 고윳값 방정식
- 2.2. 대수적 중복도와 기하학적 중복도
3. 고윳값 분해
- 3.1. 분해의 조건
- 3.2. 특수한 경우
4. 일반화된 고윳값 문제
5. 고윳값 분해의 응용
6. 유용한 사실들
7. 수치 계산
참조

1. 개요

고유값 분해는 정사각 행렬을 고유 벡터와 고유값을 사용하여 분해하는 방법이다. 행렬 A가 n개의 선형 독립적인 고유 벡터를 가지면, A = QΛQ⁻¹로 분해될 수 있으며, 여기서 Q는 A의 고유 벡터를 열로 갖는 행렬이고, Λ는 고유값을 대각 요소로 갖는 대각 행렬이다. 고유값 분해는 행렬의 거듭제곱 계산, 행렬 지수 함수 계산, 역행렬 계산 등 다양한 응용 분야에 활용된다. 일반화된 고윳값 문제와 특수한 경우의 고유값 분해, 그리고 고유값 분해의 수치 계산 방법에 대해서도 설명한다.

더 읽어볼만한 페이지

행렬 분해 - QR 분해
QR 분해는 행렬을 직교 행렬과 상삼각 행렬의 곱으로 분해하는 방법으로, 실수 또는 복소수 행렬을 직교/유니터리 행렬 Q와 상삼각 행렬 R의 곱으로 표현하여 선형대수학의 계산 및 분석에 활용되며, 그람-슈미트 과정, 하우스홀더 변환, 기븐스 회전 등 다양한 계산 방법이 존재한다.
행렬 분해 - 조르당 표준형
조르당 표준형은 대수적으로 닫힌 체 위에서 정사각 행렬을 유사 변환하여 얻을 수 있는 특정한 형태의 행렬로, 조르당 블록으로 구성되며 고윳값, 중복도, 특성/최소 다항식과 관련 있고, 스펙트럼 사영 정리, 케일리-해밀턴 정리 등 다양한 정리 증명과 행렬 계산에 응용된다.
행렬론 - 행렬식
행렬식은 정사각 행렬에 대해 정의되는 값으로, 선형 방정식의 해를 구하고 선형 독립성을 확인하며 기저의 방향과 부피를 계산하는 데 사용되며, 가우스 소거법 등의 계산 기법과 가역성 판단, 고유값 연관성 등의 성질을 갖는다.
행렬론 - 행렬 분해
행렬 분해는 주어진 행렬을 특정 성질을 갖는 여러 행렬의 곱으로 표현하는 방법으로, 수치 해석에서 행렬 알고리즘 구현 및 선형 연립 방정식 해를 구하거나 행렬 특성 분석에 활용되며 LU 분해, QR 분해, 특잇값 분해 등이 있다.
행렬 - 스핀 (물리학)
스핀은 양자역학적 각운동량으로, 양자화된 값을 가지며 자기 쌍극자 모멘트를 유발하여 다양한 분야에 응용되고 스핀트로닉스 기술 발전에 기여하지만, 전자의 스핀 기원은 아직 완전히 밝혀지지 않았다.
행렬 - 파울리 행렬
파울리 행렬은 양자역학에서 스핀을 나타내는 데 사용되는 에르미트 행렬이자 유니타리 행렬로, 행렬식은 -1이고 대각합은 0이며, 리 대수의 생성원이자 파울리 벡터로 정의되어 다양한 물리학 분야에서 활용된다.

고유값 분해
개요
분야	선형대수학
하위 분야	행렬 이론
유형별 분해
관련 항목
정의
조건
활용
계산
예시
주의사항

2. 고윳값과 고유 벡터

정사각 행렬 A에 대해, $A\mathbf{v} = \lambda \mathbf{v}$ 를 만족하는 영 벡터가 아닌 벡터 $\mathbf{v}$ 를 고유 벡터, 상수 $\lambda$ 를 고윳값이라고 한다. 기하학적으로 보면, 고유 벡터는 행렬 A에 의해 방향은 변하지 않고 크기만 변하는 벡터이며, 고윳값은 그 크기가 변하는 정도를 나타낸다.^[1]^[2]^[3]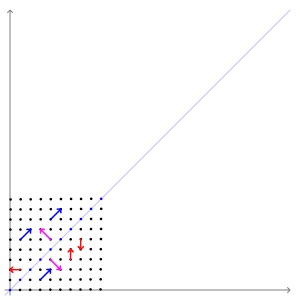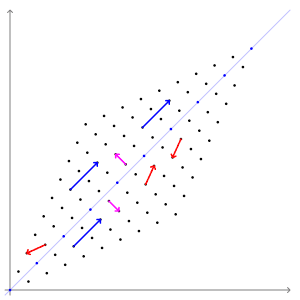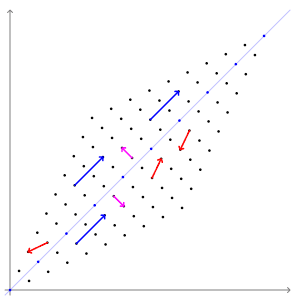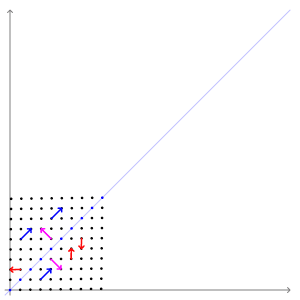

이 방정식은 다음과 같이 다시 쓸 수 있다.

:

p\left(\lambda\right) = \det\left(\mathbf{A} - \lambda \mathbf{I}\right) = 0.

여기서

p(\lambda)

는 특성 다항식이라고 불리며, 이 방정식을 특성 방정식이라고 한다. 특성 방정식은

\lambda

에 대한 N차 다항식 방정식이며,

N_{\lambda}

개의 서로 다른 해를 가진다. 이 해의 집합, 즉 고윳값은 행렬 A의 스펙트럼이라고 한다.^[1]^[2]^[3]

행렬

A\in M_d(K)

(

K

는 적절한 체)에 대해, 어떤 정칙 행렬

P

와 대각 행렬

\Lambda

가 존재하여

A=P\Lambda P^{-1}

로 쓸 수 있고, 또한

\Lambda

의 대각 성분이

A

의 고유값

\lambda_1,\dots,\lambda_d

인 (즉,

\Lambda=\mathop{\mathrm{diag}}(\lambda_1,\dots,\lambda_d)

인) 것을

A

의 고유값 분해라고 한다.^[16]^[18]

일반적으로 행렬은 고유값을 갖지 않을 수도 있고, 고유값을 갖더라도 고유값 분해가 불가능할 수 있다. 예를 들어, 실수 행렬

\bigl( \begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix} \bigr)

은 복소수 고윳값

\pm i

만 가지므로 실수 행렬로서는 고윳값을 갖지 않는다. 또한, 행렬

\bigl( \begin{smallmatrix} 2 & 1 \\ 0 & 2 \end{smallmatrix} \bigr)

은 고윳값을 갖지만 대각화 불가능하다.

d

차 행렬

A\in M_d(K)

가 대각화 가능할 필요충분 조건은

A

의 고유 벡터가

K^d

의 기저를 이루는 것, 즉 일차 독립인

A

의 고유 벡터

d

개 묶음

(v_1,\dots,v_d)

가 존재하는 것이다.^[19]

2. 1. 고윳값 방정식

:

A=\begin{pmatrix}

5 & 4 \\

0 & 1\end{pmatrix} , I는 단위행렬, det는 행렬식

:

\begin{align}\det(xI-A)&=\begin{pmatrix}x-(-5) & -4 \\

0 & x-(1)

\end{pmatrix}\\&=x^2-(-5+1)x+(-5-0)\\&=x^2 + 4 x -5\end{align}

:

x^2 + 4 x -5 = 0

:

x= 1 \;,\; -5

$x = -5$ 일때,

:

\begin{pmatrix}(-5)-(-5) & -4 \\

0 & (-5)-(1)

\end{pmatrix}

:

\begin{pmatrix}0 & -4 \\0 & -6\end{pmatrix}\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}0 \\0\end{pmatrix}

:

-4 x_2 = 0

:

-6 x_2 = 0

:

x_2 = 0

:

\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}x_1 \\0\end{pmatrix}=x_1\begin{pmatrix}1 \\0\end{pmatrix}

$x = 1$ 일때,

:

\begin{pmatrix}(1)-(-5) & -4 \\

0 & (1)-(1)

\end{pmatrix}

:

\begin{pmatrix}6 & -4 \\0 & 0\end{pmatrix}\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}0 \\0\end{pmatrix}

:

6x_1 -4x_2 = 0

:

x_1 = x_2

:

\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}x_2 \\x_2\end{pmatrix}=x_2\begin{pmatrix} \\1\end{pmatrix}

2. 2. 대수적 중복도와 기하학적 중복도

고유값의 기하학적 중복도는 관련된 고유 공간, 즉 의 영공간의 차원으로 설명될 수 있다. 대수적 중복도 또한 차원으로 생각할 수 있는데, 이는 관련된 '''일반화된 고유 공간'''(첫 번째 의미)의 차원이며, 이는 ''충분히 큰 ''에 대해 행렬 의 영공간이다. 즉, 이는 ''일반화된 고유 벡터''(첫 번째 의미)의 공간이며, 여기서 일반화된 고유 벡터는 가 충분히 여러 번 연속적으로 적용되면 ''결국'' 0이 되는 임의의 벡터이다. 모든 고유 벡터는 일반화된 고유 벡터이며, 따라서 각 고유 공간은 연관된 일반화된 고유 공간에 포함된다. 이는 기하학적 중복도가 항상 대수적 중복도보다 작거나 같다는 것을 쉽게 증명할 수 있게 해준다.

3. 고윳값 분해

Eigenvalue decomposition^영어인 고윳값 분해는 n × n 정사각 행렬 A가 n개의 선형 독립적인 고유 벡터를 가질 때, A = QΛQ⁻¹로 분해될 수 있다는 선형대수학의 행렬 분해 방법 중 하나이다. 여기서 Q는 고유 벡터를 열로 갖는 정사각 행렬이고, Λ는 고윳값을 대각 요소로 갖는 대각 행렬이다.^[16]^[18]

고유값과 고유 벡터는 다음의 선형 방정식을 만족하는 벡터와 스칼라 값이다. 정사각 행렬 A에 대해,

: $\mathbf{A} \mathbf{v} = \lambda \mathbf{v}$

여기서 v는 고유 벡터, λ는 고유값이다. 기하학적으로 고유 벡터는 A에 의해 단순히 늘어나거나 줄어드는 벡터이며, 그 양이 고유값에 해당한다.

고유값은 특성 다항식을 사용하여 찾을 수 있다.

: $p\left(\lambda\right) = \det\left(\mathbf{A} - \lambda \mathbf{I}\right) = 0.$

이 방정식은 N차 다항식 방정식이며, N_λ개의 서로 다른 해(고유값)를 갖는다. 각 고유값에 대해 특정 고유값 방정식을 풀면, 해당 고유값에 연관된 고유 벡터를 찾을 수 있다.

예를 들어, 다음과 같은 2 × 2 행렬 A를 생각해보자.

: $\begin{pmatrix}$

5 & 4 \\

0 & 1\end{pmatrix}

det는 행렬식을 의미하고, I는 단위행렬을 의미한다. 특성 방정식을 풀면:

:

\begin{align}\det(xI-A)&=\begin{pmatrix}x-(-5) & -4 \\

0 & x-(1)

\end{pmatrix}\\&=x^2-(-5+1)x+(-5-0)\\&=x^2 + 4 x -5\end{align}

:

x^2 + 4 x -5 = 0

:

x= 1 \;,\; -5

고윳값은 1과 -5이다. 각 고윳값에 대한 고유 벡터를 계산하면:

x = -5일 때:

:

\begin{pmatrix}0 & -4 \\0 & -6\end{pmatrix}\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}0 \\0\end{pmatrix}

:

x_2 = 0

이고, 고유 벡터는

x_1\begin{pmatrix}1 \\0\end{pmatrix}

이다.

x = 1일 때:

:

\begin{pmatrix}6 & -4 \\0 & 0\end{pmatrix}\begin{pmatrix}x_1 \\x_2\end{pmatrix}=\begin{pmatrix}0 \\0\end{pmatrix}

:

6x_1 = 4x_2

이고, 고유 벡터는

x_2\begin{pmatrix}\frac{2}{3} \\1\end{pmatrix}

이다.

따라서, 고유 벡터 행렬 P는 다음과 같다.

:

\begin{pmatrix}1 &  \frac{2}{3} \\0 &  1 \\\end{pmatrix}

대각화 행렬 A^D는 다음과 같이 계산된다.

:

\begin{pmatrix}1 &  -\frac{2}{3} \\0 &  1 \\\end{pmatrix}\begin{pmatrix}

5 & 4 \\

0 & 1\end{pmatrix}\begin{pmatrix}1 & \frac{2}{3} \\0 & 1 \\\end{pmatrix}=\begin{pmatrix}

5 & 0 \\

0 & 1\end{pmatrix}

결과적으로, 행렬 A의 고윳값 분해는 다음과 같다.

:

\begin{pmatrix}

5 & 4 \\

0 & 1\end{pmatrix}=\begin{pmatrix}1 & \frac{2}{3} \\0 & 1 \\\end{pmatrix}\begin{pmatrix}

5 & 0 \\

0 & 1\end{pmatrix}\begin{pmatrix}1 & -\frac{2}{3} \\0 & 1 \\\end{pmatrix}

일반적인 행렬은 고유값을 갖지 않을 수도 있으며, 고유값을 갖더라도 고유값 분해가 불가능할 수 있다. 예를 들어 행렬

\bigl( \begin{smallmatrix} 0 & -1 \\ 1 & 0 \end{smallmatrix} \bigr)

는 복소수 고유값만 가지므로 실수 행렬로 간주하면 고유값을 갖지 않는다. 또한 행렬

\bigl( \begin{smallmatrix} 2 & 1 \\ 0 & 2 \end{smallmatrix} \bigr)

는 고유값을 갖지만 대각화 불가능하다.

3. 1. 분해의 조건

행렬이 대각화 가능할 필요충분조건은 고유 벡터가 기저를 이루는 것, 즉 일차 독립인 고유 벡터가 n개 존재하는 것이다.^[19] 스펙트럼 행렬은 고유값이 서로 다르고 고유 벡터의 완전한 집합을 갖는 행렬이며, 완전히 대각화 가능하다.^[6]

3. 2. 특수한 경우

임의의 행렬 A에 대해, Λ가 대각행렬일 때, 다음과 같이 표현할 수 있다.

:

\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{-1}

:: 여기서 Q는 직교행렬이고,

\mathbf{Q}^{-1}

는 역행렬이다.

임의의 행렬 A가 대칭행렬일 때, 다음과 같이 표현할 수 있다.

:

\mathbf{A}=\mathbf{Q}\mathbf{\Lambda}\mathbf{Q}^{T}

:: 여기서 Q는 직교행렬이고,

\mathbf{Q}^{T}

는 전치행렬이다.

정규 행렬은 유니타리 행렬을 통해 대각화 가능하다. 즉, 복소수 값을 가지는 정사각 행렬 $A$ 가 정규 행렬이면( $\mathbf{A}^*\mathbf{A}=\mathbf{A} \mathbf{A}^*$ , 여기서 $\mathbf{A}^*$ 는 켤레 전치) $\mathbf{A}=\mathbf{U} \mathbf\Lambda\mathbf{U}^*$ 로 분해될 수 있다. 여기서 $\mathbf{U}$ 는 유니타리 행렬( $\mathbf{U}^*=\mathbf{U}^{-1}$ 을 의미)이며 $\mathbf{\Lambda}$ 는 대각 행렬이다.^[7]
실수 대칭행렬은 실수 직교 고유 벡터를 통해 대각화 가능하다. 즉, 모든 실수 대칭 행렬에 대해, 고유값은 실수이며 고유 벡터는 실수이고 직교로 선택될 수 있다. 따라서 실수 대칭 행렬 A는 $\mathbf{A}=\mathbf{Q} \mathbf{\Lambda}\mathbf{Q}^\mathsf{T}$ 로 분해될 수 있으며, 여기서 Q는 A의 실수, 직교 고유 벡터를 열로 갖는 직교 행렬이고, Λ는 A의 고유값을 항목으로 갖는 대각 행렬이다.^[9]
양의 정부호 행렬은 모든 고유값이 양수인 행렬이며, Cholesky 분해를 사용하여 분해할 수 있다.^[10]
유니타리 행렬은 유니타리 변환을 사용하여 대각화할 수 있다.^[8]
에르미트 행렬은 유니타리 행렬 또는 직교 행렬을 사용하여 대각화할 수 있다.^[8]

4. 일반화된 고윳값 문제

'''일반화된 고유값 문제'''는 '''A'''와 '''B'''가 행렬일 때, 다음 방정식을 만족하는 영 벡터가 아닌 벡터 v를 찾는 문제이다.

:math>\mathbf{A}\mathbf{v} = \lambda \mathbf{B} \mathbf{v}

이때, v를 '''A''', '''B'''의 ''일반화된 고유 벡터''(두 번째 의미), λ를 '''A''', '''B'''의 ''일반화된 고윳값''(두 번째 의미)이라고 부르며, 이는 일반화된 고유 벡터 v에 해당한다. λ의 가능한 값은 다음 방정식을 만족해야 한다.

:math>\det(\mathbf{A} - \lambda \mathbf{B}) = 0.

''n''개의 선형 독립적인 벡터 {'''v'''₁, …, '''v'''_''n''}}가 존재하고, 각 ''i'' ∈ {1, …, ''n''}에 대해 '''Av'''_''i'' = ''λ_i'''''Bv'''_''i''가 성립한다면, 행렬 '''P'''와 '''D'''는 다음과 같이 정의할 수 있다.

:math>P = \begin{bmatrix}

| & & | \\

\mathbf{v}_1 & \cdots & \mathbf{v}_n \\

| & & |

\end{bmatrix} \equiv

\begin{bmatrix}

(\mathbf{v}_1)_1 & \cdots & (\mathbf{v}_n)_1 \\

\vdots & & \vdots \\

(\mathbf{v}_1)_n & \cdots & (\mathbf{v}_n)_n

\end{bmatrix}

:math>(D)_{ij} = \begin{cases}

\lambda_i, & \text{if }i = j\\

0, & \text{otherwise}

\end{cases}

그러면 다음 등식이 성립한다.

:math>\mathbf{A} = \mathbf{B}\mathbf{P}\mathbf{D}\mathbf{P}^{-1}

(증명 과정은 생략)

'''A''' − ''λ'''''B''' 형태의 행렬 집합(여기서 λ는 복소수)을 ''pencil''이라고 하며, ''행렬 펜슬''이라는 용어는 행렬 ('''A''', '''B''')의 쌍을 가리키기도 한다.^[14]

'''B'''가 가역적이라면, 원래 문제는 다음과 같이 쓸 수 있다.

:math>\mathbf{B}^{-1}\mathbf{A}\mathbf{v} = \lambda \mathbf{v}

이는 표준적인 고유값 문제이다. 그러나 대부분의 상황에서는 역변환보다 원래 명시된 대로 일반화된 고유값 문제를 푸는 것이 더 바람직하다. 특히 '''A'''와 '''B'''가 에르미트 행렬인 경우에는 '''B'''⁻¹'''A'''가 일반적으로 에르미트 행렬이 아니므로 해의 중요한 특성이 나타나지 않기 때문이다.

'''A'''와 '''B'''가 모두 대칭이거나 에르미트 행렬이고, '''B'''가 양의 정부호 행렬이기도 하다면, 고유값 ''λ_i''는 실수이고 서로 다른 고유값을 가진 고유 벡터 '''v'''₁과 '''v'''₂는 '''B'''-직교한다. ('''v'''₁^*'''Bv'''₂ = 0).^[15] 이 경우, 일반화된 고유 벡터의 기저가 존재한다(이는 결함 있는 문제가 아니다).^[14] 이 경우는 때때로 ''에르미트 정부호 펜슬'' 또는 ''정부호 펜슬''이라고 불린다.^[14]

5. 고윳값 분해의 응용

선형대수학에서 고윳값 분해는 다음과 같은 장점이 있다.^[16]^[17]^[18]

거듭제곱 계산 간소화: 행렬 A가 고윳값 분해를 가지면, A의 거듭제곱은 대각 행렬의 거듭제곱으로 쉽게 계산할 수 있다.
행렬 함수 계산: 행렬 지수 함수와 같은 거듭제곱 급수 계산을 간편하게 한다. 행렬 지수 함수는 각 고윳값에 대한 지수 함수를 대각선 원소로 갖는 대각 행렬을 이용하여 계산할 수 있다.
역행렬 계산: 행렬 A를 고윳값 분해할 수 있고 고윳값 중 0이 없다면, A는 가역이며, 그 역행렬은 고윳값 분해를 통해 쉽게 구할 수 있다.^[4] 대칭행렬의 경우, 고유 벡터로 구성된 행렬은 직교 행렬이 되므로 역행렬 계산이 더욱 간편하다.
데이터 행렬 응용: 고윳값 분해는 실제 데이터 행렬에도 응용될 수 있다. 이 때, 작은 고윳값은 역행렬에 큰 영향을 주어 해를 방해할 수 있는데, 이를 완화하기 위해 작은 고윳값을 제거하거나 확장하는 방법이 제안된다.

5. 1. 행렬의 거듭제곱 계산

행렬

A

가 고유값 분해

A=P\Lambda P^{-1}

를 갖는다고 가정하자. 이때, 자연수

n

에 대해

A

의 거듭제곱

A^n

은 다음과 같이 나타낼 수 있다.^[16]^[17]^[18]

:

\begin{align}A^n&= (P\Lambda P^{-1})^n\\&= (P\Lambda P^{-1})(P\Lambda P^{-1})\cdots(P\Lambda P^{-1})\\&= P\Lambda^n P^{-1}\end{align}

\Lambda

는 대각 행렬이므로,

\Lambda=\mathop{\mathrm{diag}}(\lambda_1,\dots,\lambda_d)

에 대해

\Lambda^n=\mathop{\mathrm{diag}}(\lambda_1^n,\dots,\lambda_d^n)

으로 계산할 수 있다. 따라서,

A

에 대해

P

가 알려져 있을 경우

A

의 거듭제곱을 간단하게 구할 수 있다.

예를 들어 행렬

:

\begin{pmatrix}

5 & 4 \\

0 & 1\end{pmatrix}=\begin{pmatrix}1 & \\0 & 1 \\\end{pmatrix}\begin{pmatrix}

5 & 0 \\

0 & 1\end{pmatrix}\begin{pmatrix}1 & - \\0 & 1 \\\end{pmatrix}

는 고유값 분해를 통해 거듭제곱을 쉽게 계산할 수 있다.

:

f(x) = a_0 + a_1 x + a_2 x^2 + \cdots

가 주어지면,

:

f(A) = Q f(\Lambda) Q^{-1}

임을 알 수 있다.

\Lambda

가 대각 행렬이므로,

f(\Lambda)

는 다음과 같이 쉽게 계산된다.

:

[f(\Lambda)]_{ii} = f(\lambda_i)

즉,

f(\Lambda)

의 비대각 요소는 0이며,

f(\Lambda)

또한 대각 행렬이다. 따라서

f(A)

를 계산하는 것은 각 고유값에 대한 함수를 계산하는 것으로 단순화된다.

유사한 방법으로 정칙 함수 미적분학을 사용하여,

:

A^{-1} = Q \Lambda^{-1} Q^{-1}

를 통해 다음을 얻는다.

:

[f(\Lambda)]_{ii} = f(\lambda_i)

:

\begin{align}A^2 &= \left(Q\Lambda Q^{-1}\right) \left(Q\Lambda Q^{-1}\right)= Q\Lambda\left(Q^{-1}Q\right)\Lambda Q^{-1}= Q\Lambda^2 Q^{-1} \\[1.2ex]A^n &= Q\Lambda^n Q^{-1}\\[1.2ex]\exp A&= Q \exp(\Lambda) Q^{-1}\end{align}

이는 함수

f(x)=x^2, \; f(x)=x^n, \; f(x)=\exp{x}

에 대한 예시이다. 또한,

\exp{A}

는 행렬 지수이다.

5. 2. 행렬 지수 함수

고유값 분해는 행렬의 거듭제곱 급수를 훨씬 쉽게 계산할 수 있도록 해준다. 특히 행렬 지수 함수

e^A

는 다음과 같이 계산할 수 있다.^[16]^[17]^[18]

:

\begin{align}e^A&= e^{P\Lambda P^{-1}}\\&= Pe^\Lambda P^{-1}\\&= P\left(\sum_{x=0}^\infty\frac{1}{n!}\Lambda^n \right)P^{-1}\\&= P\left(\begin{smallmatrix} e^{\lambda_1} & & & \\ & e^{\lambda_2} & & \\ & & \ddots & \\ & & & e^{\lambda_d} \end{smallmatrix}\right)P^{-1}\end{align}

여기서

A=P\Lambda P^{-1}

는

A

의 고유값 분해이고,

\Lambda

는 대각 행렬이므로,

e^{\Lambda}

는 각 고윳값

\lambda_i

에 대한 지수 함수

e^{\lambda_i}

를 대각선 원소로 갖는 대각 행렬이 된다.

5. 3. 역행렬

행렬 A를 고유값 분해할 수 있고, 고유값 중 0이 없는 경우 A는 가역이며, 역행렬은 다음과 같이 주어진다.^[4]

:

\mathbf{A}^{-1} = \mathbf{Q}\mathbf{\Lambda}^{-1}\mathbf{Q}^{-1}

A가 대칭행렬이면, Q는 A의 고유 벡터로 구성되므로, Q는 직교 행렬이 되며, 따라서 Q^-1 = Q^T이다. 또한, Λ는 대각 행렬이므로, 역행렬을 구하기가 쉽다.

:

\left[\mathbf{\Lambda}^{-1}\right]_{ii} = \frac{1}{\lambda_i}

5. 4. 기타 응용

고유값 분해는 측정된 실제 데이터의 행렬에 사용될 때, 모든 고유값을 수정하지 않고 사용하면 역함수가 덜 유효할 수 있다. 이는 고유값이 상대적으로 작아질수록 역행렬에 대한 기여도가 커지기 때문이다. 0에 가깝거나 측정 시스템의 "노이즈"에 있는 고유값은 과도한 영향을 미치며 역행렬을 사용한 해(탐지)를 방해할 수 있다.^[4]

이러한 문제를 완화하기 위해 두 가지 방법이 제안되었다. 첫 번째는 작은 고유값이나 0인 고유값을 제거하는 것이다. 이 방법은 원래 행렬의 희소 표본과 유사하며, 중요하지 않다고 판단되는 요소를 제거한다. 그러나 해 또는 탐지 과정이 노이즈 수준에 가까운 경우, 이 방법은 원하는 해에 영향을 미치는 요소를 제거할 수 있다는 단점이 있다.

두 번째 방법은 고유값을 확장하여 낮은 값이 역행렬에 미치는 영향을 줄이는 것이다. 이 방법은 낮은 고유값의 영향은 줄이면서도, 여전히 기여하도록 하여 노이즈 근처의 해를 찾을 수 있게 한다.

신뢰할 수 있는 고유값은, 매우 유사하고 낮은 값의 고유값이 측정 노이즈(대부분의 시스템에서는 낮다고 가정)를 잘 나타낸다고 가정하여 찾을 수 있다.

고유값이 값에 따라 정렬된 경우, 정렬된 고유값의 라플라스 연산자를 최소화하여 신뢰할 수 있는 고유값을 찾을 수 있다.^[5]

:

여기서 고유값은 정렬되었음을 나타내기 위해 s|에스^영어로 아래첨자 처리된다. 최소화 위치는 가장 신뢰할 수 있는 가장 낮은 고유값이다. 측정 시스템에서 이 신뢰할 수 있는 고유값의 제곱근은 시스템 구성 요소에 대한 평균 노이즈이다.

6. 유용한 사실들

에르미트 행렬의 고유 벡터는 서로 직교하도록 선택할 수 있다.^[9] 퇴화된 고유값의 경우, 고유 벡터는 선형 변환의 추가적인 자유도를 갖는다. 즉, 고유값(퇴화 부분 공간)을 공유하는 고유 벡터의 모든 선형(직교) 조합 자체가 부분 공간에서 고유 벡터가 된다.

고윳값들의 곱은 행렬의 행렬식과 같다.^[1]

$\det\left(\mathbf{A}\right) = \prod_{i=1}^{N_\lambda}{\lambda_i^{n_i} }$

여기서 각 고유값은 대수적 중복도인 ${n_i}$ 제곱으로 표현된다.

고윳값들의 합은 행렬의 대각합과 같다.^[2]

$\operatorname{tr}\left(\mathbf{A}\right) = \sum_{i=1}^{N_\lambda}{ {n_i}\lambda_i}$

여기서 각 고유값은 대수적 중복도인 ${n_i}$ 에 곱해진다.

만약 행렬 $\mathbf{A}$ 의 고유값이 $\lambda_i$ 이고, $\mathbf{A}$ 가 가역 행렬이라면, $\mathbf{A}^{-1}$ 의 고유값은 $\lambda_i^{-1}$ 이다. 만약 $\mathbf{A}$ 의 고유값이 $\lambda_i$ 라면, 정칙 함수인 모든 $f$ 에 대해 $f(\mathbf{A})$ 의 고유값은 $f(\lambda_i)$ 이다.

$\mathbf{A}$ 가 에르미트 행렬이고 full-rank(정칙 행렬)이라면, 고유 벡터의 기저는 서로 직교하도록 선택될 수 있다. 고유값은 실수이다.

$\mathbf{A}^{-1}$ 의 고유 벡터는 $\mathbf{A}$ 의 고유 벡터와 같다.

고유 벡터는 곱셈 상수를 제외하고 정의된다. 즉, 만약 $\mathbf{Av} = \lambda \mathbf{v}$ 라면, 모든 스칼라 $c \neq 0$ 에 대해 $c\mathbf{v}$ 도 고유 벡터이다. 특히, $-\mathbf{v}$ 및 $e^{i\theta}\mathbf{v}$ (모든 $\theta$ 에 대해) 역시 고유 벡터이다.

7. 수치 계산

큰 행렬의 고유값은 특성 다항식을 사용하지 않고 반복적인 수치적 방법을 통해 계산한다. 아벨-루피니 정리에 따르면 5차 이상의 다항식의 근은 일반적으로 n제곱근을 사용하여 표현할 수 없기 때문에, 고유값과 고유 벡터를 찾는 일반적인 알고리즘은 반복적이다.^[11]

뉴턴 방법과 같은 반복적 수치 알고리즘이 존재하지만, 특성 다항식을 계산하고 이러한 방법을 적용하는 것은 계수의 작은 반올림 오차가 고유값과 고유 벡터에 큰 오차를 유발할 수 있어 비실용적이다.^[11]

간단하고 정확한 반복 방법은 거듭제곱 방법이다. 임의의 벡터에서 시작하여 다음 단위 벡터 수열을 계산한다.

$\frac{\mathbf{A}\mathbf{v}}{\left\|\mathbf{A}\mathbf{v}\right\|}, \frac{\mathbf{A}^2\mathbf{v}}{\left\|\mathbf{A}^2\mathbf{v}\right\|}, \frac{\mathbf{A}^3\mathbf{v}}{\left\|\mathbf{A}^3\mathbf{v}\right\|}, \ldots$

이 수열은 가장 큰 크기의 고유값에 해당하는 고유 벡터로 수렴한다. 구글은 이 방법을 페이지랭크 계산에 사용한다.^[12] 아르놀디 반복과 QR 알고리즘도 거듭제곱 방법에서 발전된 알고리즘이다.^[11]

고유값을 계산한 후에는 다음 방정식을 풀어 고유 벡터를 계산할 수 있다.

$\left(\mathbf{A} - \lambda_i \mathbf{I}\right)\mathbf{v}_{i,j} = \mathbf{0}$

이 방정식은 가우스 소거법 등의 방법으로 풀 수 있다.

하지만 실제로는 고유 벡터를 고유값 계산 과정에서 함께 구하는 경우가 많다. 예를 들어 멱승법에서는 고유 벡터를 먼저 계산하고, 고유값은 레일리 몫으로 계산된다.^[11] 에르미트 행렬의 경우 QR 알고리즘에서 정규 직교 고유 벡터를 얻을 수 있다.^[11] 분할 정복 고유값 알고리즘은 고유 벡터와 고유값을 모두 구할 때 QR 알고리즘보다 효율적이다.^[11]

참조

_[1] 서적 Matrix Computations Johns Hopkins University Press
_[2] 서적 Advanced Engineering Mathematics https://archive.org/[...] Wiley
_[3] 서적 Linear Algebra and Matrix Theory Wiley
_[4] 간행물 Observations on relationship between eigenvalues, instrument noise and detection performance
_[5] 간행물 Refinement and generalization of the extension method of covariance matrix inversion by regularization
_[6] 서적 Numerical linear algebra https://archive.org/[...] Springer 2008
_[7] 서적
_[8] 웹사이트 Applied linear algebra and matrix analysis https://archive.org/[...] 2006
_[9] 서적
_[10] 서적 Matrix analysis and applied linear algebra Society for Industrial and Applied Mathematics
_[11] 서적 Numerical Linear Algebra SIAM
_[12] 문서 Ipsen, Ilse, and Rebecca M. Wills, Analysis and Computation of Google's PageRank https://www4.ncsu.ed[...] 2018-09-21
_[13] 서적 Numerical Mathematics https://books.google[...] Springer
_[14] 서적 Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide https://cs.utk.edu/~[...] SIAM 2022-09-09
_[15] 서적 The symmetric eigenvalue problem https://epubs.siam.o[...] Society for Industrial and Applied Mathematics 1998
_[16] 웹사이트 Eigen Decomposition http://mathworld.wol[...]
_[17] 문서 The eigen-decomposition: Eigenvalues and eigenvectors
_[18] 서적 Introduction to linear algebra Wellesley-Cambridge Press
_[19] 서적 線形代数学 https://www.worldcat[...] 京都大学学術出版会 2009-06
_[20] 간행물 An eigendecomposition approach to weighted graph matching problems
_[21] 간행물 Unitary root-MUSIC with a real-valued eigendecomposition: A theoretical and experimental performance study
_[22] 간행물 Analysis of the performance and sensitivity of eigendecomposition-based detectors
_[23] 간행물 A new high resolution color flow system using an eigendecomposition-based adaptive filter for clutter rejection
_[24] 간행물 Eigendecomposition-based clutter filtering technique for optical microangiography

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com