맨위로가기

구글 행렬

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

구글 행렬은 페이지 또는 노드 간의 관계를 나타내는 인접 행렬을 기반으로 구성되며, 웹 페이지의 중요도를 평가하는 데 사용되는 페이지랭크 알고리즘의 핵심 요소이다. 구글 행렬은 마르코프 연쇄의 전이 행렬을 변형하여 생성되며, 감쇠 인자를 포함하여 임의의 페이지로의 점프 확률을 반영한다. 이 행렬은 고유값과 고유벡터를 가지며, 가장 큰 고유값에 해당하는 고유벡터는 페이지랭크 벡터로, 각 페이지의 상대적 중요도를 나타낸다. 구글 행렬은 위키백과 네트워크 분석, 생물학적 네트워크 분석, 사회 연결망 분석 등 다양한 분야에 응용되며, 1998년 세르게이 브린과 래리 페이지에 의해 처음 기술되었다.

더 읽어볼만한 페이지

  • 구글 검색 - 구글 쇼핑
    구글 쇼핑은 상품 검색, 개인화 추천, 가격 비교, 구매 가이드, 인근 매장 정보, 구글 보증 구매 등을 제공하는 구글의 온라인 쇼핑 서비스로, 검색 결과나 웹사이트, 모바일 앱을 통해 이용 가능하며, 2002년 Froogle로 시작하여 현재 121개국에서 서비스 중이다.
  • 구글 검색 - 구글 도서
    구글 도서는 2002년에 시작된 구글의 도서 디지털화 프로젝트로, 전 세계 도서관과 제휴하여 도서를 스캔하고 온라인에서 검색 및 열람을 가능하게 하며, 저작권 문제와 스캔 오류 등으로 비판을 받기도 했다.
  • 마르코프 모형 - 강화 학습
    강화 학습은 에이전트가 환경과의 상호작용을 통해 누적 보상을 최대화하는 최적의 정책을 학습하는 기계 학습 분야이며, 몬테카를로 방법, 시간차 학습, Q-러닝 등의 핵심 알고리즘과 탐험과 활용의 균형, 정책 경사법 등의 다양한 연구 주제를 포함한다.
  • 마르코프 모형 - 칼만 필터
    칼만 필터는 잡음이 있는 측정값들을 이용하여 선형 동적 시스템의 상태를 추정하는 재귀 필터로, 예측과 보정 단계를 반복하며 항법 시스템, 레이더 추적, 컴퓨터 비전 등 다양한 분야에 응용된다.
구글 행렬
구글 행렬
유형마르코프 행렬
속성열-정규화됨
용도웹페이지 순위 결정
추가 정보
관련 항목페이지랭크
허브
권위
랜덤 서퍼 모델

2. 구글 행렬의 구성

구글 행렬은 웹 페이지 간의 연결 관계를 나타내는 인접 행렬을 기반으로 만들어지며, 몇 단계를 거쳐 구성된다.

2. 1. 인접 행렬 ''A''

총 ''N''개의 페이지가 있다고 가정하면, 행렬 ''A''는 다음과 같이 채워진다.

  • 행렬 요소 A_{i, j}는 노드 j가 노드 i에 링크를 가지고 있으면 1, 그렇지 않으면 0이다. 이것은 링크의 인접 행렬이다.[1]

2. 2. 마르코프 행렬 ''S''

인접 행렬 ''A''를 기반으로 각 열의 합이 1이 되도록 정규화한 행렬이다. 댕글링 노드(외부로 나가는 링크가 없는 노드)는 모든 다른 노드로 연결되는 것으로 간주하여 처리한다.[1]

주어진 네트워크의 마르코프 연쇄 전이에 해당하는 관련 행렬 ''S''는 ''A''로부터 구성된다. 열 "j"의 요소를 k_j=\Sigma_{i=1}^N A_{i,j}로 나누어 계산하며, 여기서 k_j는 노드 ''j''에서 다른 모든 노드로의 총 발신 링크 수이다. 행렬 요소가 0인 열, 즉 댕글링 노드에 해당하는 열은 상수 값 ''1/N''으로 대체된다. 이러한 절차는 모든 싱크, 즉 댕글링 상태 a 에서 다른 모든 노드로 링크를 추가한다.[1]

결과적으로, 구성에 의해 행렬 ''S''의 임의의 열에 있는 모든 요소의 합은 1이 된다. 이러한 방식으로 행렬 ''S''는 수학적으로 잘 정의되며, 마르코프 연쇄 클래스와 페론-프로베니우스 연산자 클래스에 속한다. 이는 ''S''를 페이지랭크 알고리즘에 적합하게 만든다.[1]

2. 3. 구글 행렬 ''G''

최종 구글 행렬 ''G''는 ''S''를 통해 다음과 같이 표현될 수 있다.

:G_{ij} = \alpha S_{ij} + (1-\alpha) \frac{1}{N} \;\;\;\;\;\;\;\;\;\;\; (1)

구성에 따라 각 행렬 열 내의 모든 음수가 아닌 요소의 합은 1과 같다. 수치 계수 \alpha 는 감쇠 인자로 알려져 있다.

일반적으로 ''S''는 희소 행렬이며, 현대의 방향성 네트워크의 경우 한 줄 또는 한 열에 약 10개의 0이 아닌 요소만 있으므로, 벡터와 행렬 ''G''를 곱하는 데 약 10''N''번의 곱셈만 필요하다.[2][3] CheiRank 기사에서는 식(1)을 통해 간단한 네트워크 내에서 행렬 S 를 구성하는 예시를 보여준다.

실제 행렬을 위해 구글은 0.85 부근의 감쇠 인자 \alpha를 사용한다.[2][3][4] 항 (1-\alpha)는 서퍼가 임의의 페이지로 점프할 확률을 나타낸다. 행렬 G는 마르코프 연쇄의 페론-프로베니우스 연산자 종류에 속한다.[2] 구글 행렬 구조의 예시는 2009년 위키백과 문서 하이퍼링크 네트워크를 작은 규모로 나타낸 그림 1과, 2006년 케임브리지 대학교 네트워크를 큰 규모로 나타낸 그림 2에 나와 있다.

260px

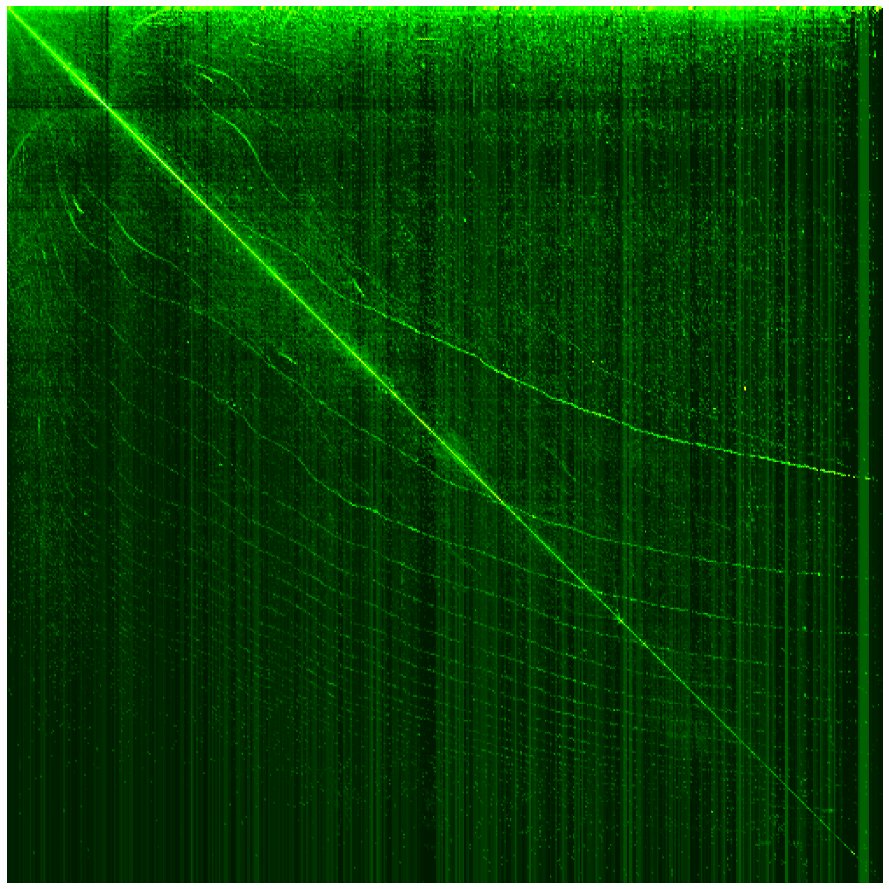
3. 구글 행렬의 수학적 특성

구글 행렬은 마르코프 연쇄의 일종으로, 페론-프로베니우스 정리에 따라 가장 큰 고유값은 1이며, 이에 해당하는 고유벡터(페이지랭크 벡터)는 모든 요소가 양수인 정상 확률 분포를 나타낸다.

3. 1. 고유값 스펙트럼

0 < \alpha < 1 일 때, 구글 행렬은 최대 하나의 고유값 \lambda =1을 갖는다. 이 고유값에 해당하는 우측 고유벡터는 음수가 아닌 요소 P_i 를 가지며, 이는 정상 확률 분포로 해석될 수 있다.[2] 이 확률값을 감소하는 순서대로 정렬하면 웹 페이지 순위를 매기는 데 사용되는 페이지랭크 벡터 P_i 와 페이지랭크 K_i 를 얻을 수 있다. 월드 와이드 웹의 경우, 일반적으로 P \propto 1/K^{\beta}이며, 여기서 \beta \approx 0.9 이다. 주어진 페이지랭크 값을 갖는 노드 수는 지수 \nu = 1+1/\beta \approx 2.1 에 따라 N_P \propto 1/P^\nu 로 증가한다.[6][7] \lambda =1에서의 좌측 고유벡터는 상수 행렬 요소를 갖는다. 0 < \alpha 일 때, 최대 고유값 \lambda =1을 제외한 모든 고유값은 \lambda_i \rightarrow \alpha \lambda_i 로 변화한다.[2] 페이지랭크 벡터는 \alpha 에 따라 달라지지만, \lambda_i < 1 인 다른 고유벡터는 \lambda = 1 에서의 상수 좌측 벡터와의 직교성으로 인해 변하지 않는다. \lambda = 1 과 다른 고유값 사이의 간격은 1 - \alpha \approx 0.15가 되므로, 무작위 초기 벡터는 약 50번의 G 행렬 곱셈을 통해 페이지랭크로 빠르게 수렴한다.

\alpha=1 인 경우, 행렬 G 는 일반적으로 여러 개의 중복된 고유값 \lambda =1 을 가질 수 있다.[8] 다양한 방향성 네트워크에서 구글 행렬 고유값 스펙트럼의 예시는
280px
와
350px
에서 확인할 수 있다.

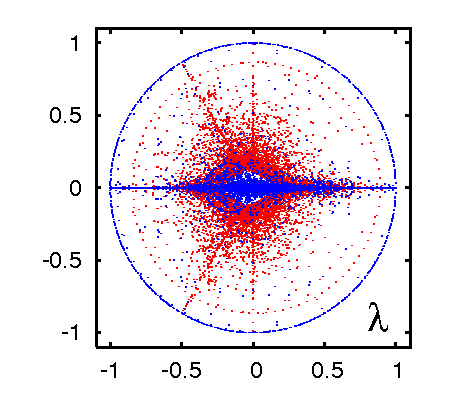
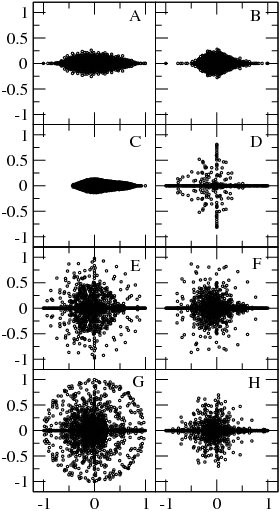
구글 행렬은 동적 맵에 대한 Ulam 방법을 통해 생성된 Ulam 네트워크에도 적용할 수 있다. 이러한 행렬의 스펙트럼 특성은 여러 연구에서 논의되었으며,[5][9] 많은 경우 스펙트럼이 프랙탈 바일 법칙을 따르는 것으로 나타났다.

280px


\lambda_i


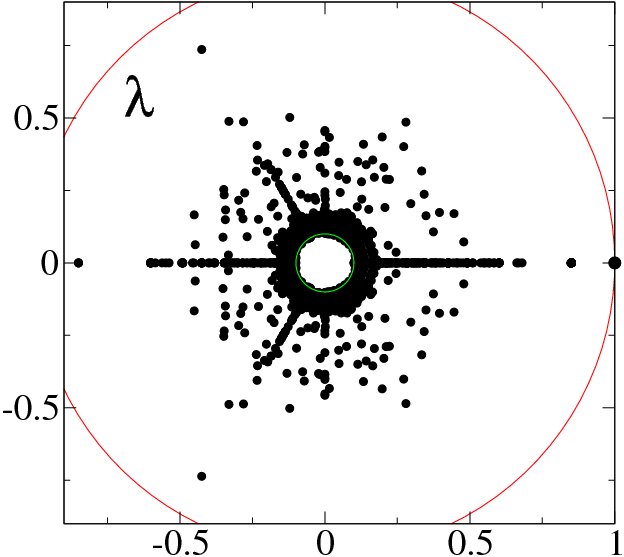
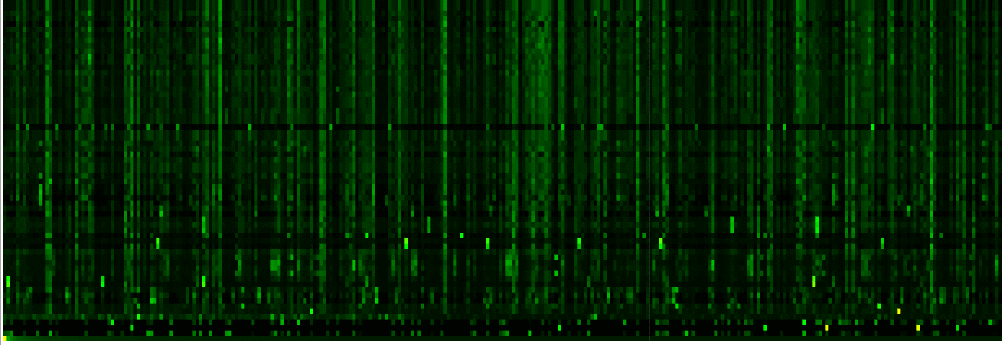
리눅스 커널 소프트웨어의 프로시저 호출 네트워크와 같은 다른 방향성 네트워크에도 구글 행렬을 구성할 수 있다. 이 경우 \lambda 의 스펙트럼은 프랙탈 차원 d \approx 1.3 인 프랙탈 바일 법칙으로 설명된다(그림 5 참조).[9] 수치 분석에 따르면 행렬 G 의 고유 상태는 국소화된다(그림 6 참조).[9] 아놀디 반복 방법을 사용하면 상당히 큰 크기의 행렬에 대해서도 많은 고유값과 고유 벡터를 계산할 수 있다.[5][9]

G 행렬의 다른 예로는 뇌의 구글 행렬 및 비즈니스 프로세스 관리가 있으며, DNA 서열에 대한 구글 행렬 분석의 적용도 연구되었다.[1] 또한, 이러한 구글 행렬 접근 방식을 통해 여러 언어의 위키백과 개인 관련 기사 순위를 매겨 문화 간의 연관성을 분석할 수도 있다.

3. 2. 고유벡터 (페이지랭크 벡터)

0 < \alpha < 1 일 때, 구글 행렬은 최대 하나의 고유값 \lambda =1을 가지며, 이에 대응하는 우측 고유벡터는 음이 아닌 요소 P_i 를 갖는다. 이 요소들은 정상 확률 분포로 해석할 수 있다.[2] 이 확률들을 감소하는 값의 순서대로 정렬하면, 구글 검색에서 웹 페이지 순위를 매기는 데 사용되는 페이지랭크 벡터 P_i 와 페이지랭크 K_i 를 얻을 수 있다. 일반적으로 월드 와이드 웹의 경우 페이지랭크는 P \propto 1/K^{\beta}이며, 여기서 \beta \approx 0.9 이다. 주어진 페이지랭크 값을 갖는 노드의 수는 지수 \nu = 1+1/\beta \approx 2.1 에 따라 N_P \propto 1/P^\nu 로 증가한다.[6][7] 즉, 소수의 페이지가 매우 높은 페이지랭크를 갖는 경향을 보인다.

\lambda =1에서의 좌측 고유벡터는 상수 행렬 요소를 갖는다. 0 < \alpha 일 때, 최대 고유값 \lambda =1을 제외한 모든 고유값은 \lambda_i \rightarrow \alpha \lambda_i 로 변화한다.[2] 페이지랭크 벡터는 \alpha 에 따라 달라지지만, \lambda_i < 1 인 다른 고유벡터는 \lambda = 1 에서의 상수 좌측 벡터와의 직교성으로 인해 변하지 않는다. \lambda = 1 과 다른 고유값 간의 간격은 1 - \alpha \approx 0.15가 되므로, 무작위 초기 벡터는 약 50번의 G 행렬 곱셈을 통해 페이지랭크로 빠르게 수렴한다.

\alpha=1 에서, 행렬 G 는 종종 여러 개의 중복된 고유값 \lambda =1 을 갖는다.[8]

아놀디 반복 방법을 사용하면 상당히 큰 크기의 행렬에서도 많은 고유값과 고유 벡터를 계산할 수 있다.[5][9]

4. 구글 행렬의 응용

구글 행렬은 웹 페이지의 순위를 결정하는 것 외에도 다양한 분야에 응용될 수 있다.

5. 역사적 배경

감쇠 인자를 포함하는 구글 행렬은 1998년 세르게이 브린과 래리 페이지에 의해 기술되었으며, 페이지랭크의 역사에 관한 기사도 참고할 수 있다.

참조

[1] 논문 Towards two-dimensional search engines
[2] 서적 Google's PageRank and Beyond Princeton University Press
[3] 웹사이트 How Google Finds Your Needle in the Web's Haystack http://www.ams.org/s[...] AMS Feature Columns
[4] 웹사이트 PageRank Lecture 12 https://www.cs.cmu.e[...] 2008-10-09
[5] 논문 Universal emergence of PageRank 2011-11-01
[6] 논문 Large scale properties of the Webgraph http://www.cosinproj[...] 2004-03-30
[7] 논문 Using PageRank to Characterize Web Structure http://cs.brown.edu/[...]
[8] 논문 Spectral properties of the Google matrix of the World Wide Web and other directed networks 2010-05-25
[9] 논문 Fractal Weyl law for Linux Kernel Architecture


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com