구조 인자

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 정의
3. 다양한 격자 유형의 구조 인자
4. 완전 결정 및 불완전 결정
5. 액체의 구조 인자
참조

1. 개요

구조 인자는 결정 구조의 산란 파수에 대한 복소 함수로, 결정 내 입자들의 위치에 따라 결정된다. 기하학적 구조 인자로도 불리며, 동역학적 구조 인자와 구별된다. 구조 인자는 결정학에서 격자와 기저를 분리하여 취급하며, 다양한 격자 유형에 따라 다른 값을 가진다. 체심 입방체(BCC), 면심 입방체(FCC), 다이아몬드 구조, 섬아연석 구조(Zincblende), 염화 세슘, 육방 밀집 구조(HCP) 등 다양한 결정 구조의 구조 인자가 존재한다. 또한, 완전 결정과 불완전 결정의 차이를 설명하며, 유한 크기 효과, 제1종 및 제2종 무질서, 액체의 구조 인자 등 다양한 요소를 고려하여 분석된다.

더 읽어볼만한 페이지

결정학 - 점군
점군은 도형의 병진 조작을 제외한 대칭 조작들의 집합으로 군론의 공리를 만족하며, 쉐인플리스 기호나 허먼-모건 기호로 표기되고, 대칭 조작에 대응하는 행렬 표현은 가약 표현과 기약 표현으로 분해될 수 있다.
결정학 - 역격자
역격자는 브라베 격자의 쌍대 개념으로, 해당 격자의 모든 벡터와의 내적이 정수가 되는 벡터들의 집합으로 정의되며, 결정 구조 분석 및 블로흐 정리와 관련된 브릴루앙 영역 연구에 활용되는 또 다른 브라베 격자이다.

구조 인자
결정학적 정보
정의	결정 내에서 단위 세포가 반복되는 방식과 관련하여 파동이 어떻게 간섭하는지를 설명하는 수학적 함수
기호	F(hkl)
관련 분야	X선 회절, 결정학
적용	결정 구조 분석, 재료 과학
구조 인자 (Structure Factor)
정의 (수학적 표현)	F(hkl) = Σᵢ fᵢ exp[2πi(hxᵢ + kyᵢ + lzᵢ)]
F(hkl)	구조 인자 (hkl)
fᵢ	원자 산란 인자
xᵢ, yᵢ, zᵢ	단위 세포 내 i번째 원자의 분수 좌표
h, k, l	밀러 지수
구조 인자 계산의 중요성
결정 구조 결정	실험적인 회절 데이터 해석 및 결정 구조 모델 개선에 필수적임.
재료 특성 예측	재료의 전자적, 광학적 특성 예측에 사용될 수 있음.
추가 정보
설명	결정 내 원자의 위치와 종류에 따라 X선, 중성자 또는 전자와 같은 파동이 어떻게 산란되는지 설명함.
활용	회절 패턴의 강도를 예측하고, 실험적으로 얻은 회절 데이터로부터 결정 구조를 결정하는 데 사용됨.

2. 정의

결정의 원시세포 내에 $\nu$ 개의 입자들이 $\mathbf{d}_i$ 에 위치한다고 할 때, 이 결정 구조의 '''구조 인자''' $S(\mathbf{K})$ 는 입사 파수 변화 $\mathbf{K}$ 에 대한 복소 함수로, 다음과 같이 정의된다.^[1]

: $S(\mathbf{K}) = \sum_{i=1}^\nu \exp(i\mathbf{K} \cdot \mathbf{d}_i)$ .

산란하는 입자의 에너지에 따라 달라지는 '''동역학적 구조 인자'''(dynamical structure factor^영어)를 정의하기도 하는데, 이때 위에 정의된 구조 인자는 '''기하학적 구조 인자'''(geometric structure factor^영어)로 구별한다.^[2]

3. 다양한 격자 유형의 구조 인자

결정의 원시세포 내에 $\nu$ 개의 입자들이 $\mathbf d_i$ 에 위치한다고 할 때, 이 결정 구조의 '''구조 인자''' $S(\mathbf K)$ 는 입사 파수 변화 $\mathbf K$ 에 대한 복소 함수로 다음과 같이 주어진다.

: $S(\mathbf K)=\sum_{i=1}^\nu\exp(i\mathbf K\cdot\mathbf d_i)$ .

산란하는 입자의 에너지에 따라 달라지는 '''동역학적 구조 인자'''(dynamical structure factor^영어)를 정의하기도 하는데, 이때는 위에서 정의한 구조 인자를 '''기하학적 구조 인자'''(geometric structure factor^영어)라고 구분한다.

결정학에서, 기저와 격자는 별도로 취급된다. 완벽한 결정의 경우, 격자는 역격자를 제공하며, 이는 회절 빔의 위치(각도)를 결정하고, 기저는 구조 인자 $F_{hkl}$ 을 제공하며, 이는 회절 빔의 진폭과 위상을 결정한다.^[4]

: $F_{hk\ell} = \sum_{j=1}^N f_j \mathrm{e}^{[-2 \pi i (h x_j + k y_j + \ell z_j)]}$

여기서 합은 단위 세포 내의 모든 원자에 대한 것이고, $x_j, y_j, z_j$ 는 $j$ 번째 원자의 위치 좌표이며, $f_j$ 는 $j$ 번째 원자의 산란 인자이다. 좌표 $x_j, y_j, z_j$ 는 격자 벡터 $\mathbf{a},\mathbf{b},\mathbf{c}$ 의 방향과 차원을 갖는다. $F_{hk\ell}$ 는 단위 세포 내의 모든 원자로부터의 파동의 벡터 합이다. 임의의 격자점에 있는 원자는 모든 $hk\ell$ 에 대해 기준 위상각 0을 갖는데, 그 이유는 $(h x_j + k y_j + \ell z_j)$ 가 항상 정수이기 때문이다.

파장 $\lambda$ 의 빔이 $N$ 개의 입자 또는 원자 집합에 의해 산란되는 과정을 고려해 보자. 이들은 위치 $\textstyle \mathbf{R}_{j}, j = 1, \, \ldots, \, N$ 에 정지해 있다. 산란이 약하다고 가정하여(본 근사) 흡수, 굴절 및 다중 산란은 무시할 수 있다(운동학적 회절). 산란파의 방향은 산란 벡터 $\mathbf{q}$ 로 정의된다. $\mathbf{q} = \mathbf{k_s} - \mathbf{k_o}$ 이고, 여기서 $\mathbf{k_s}$ 와 $\mathbf{k_o}$ ( $| \mathbf{k_s} | = |\mathbf{k_0}| = 2\pi/\lambda$ )는 산란 빔 및 입사 빔 파수 벡터이고, $\theta$ 는 그 사이의 각도이다. 탄성 산란의 경우, $|\mathbf{k}_s| = |\mathbf{k_o}|$ 이고 $q = |\mathbf{q}| = {\frac {4 \pi}{\lambda} \sin (\theta/2)}$ 이며, $\mathbf{q}$ 의 가능한 범위를 제한한다(에발트 구).^[1]^[2]

원자 집합의 경우, $f_j$ 는 $j$ 번째 원자의 원자 폼 팩터이다. 구조 인자는 이 강도를 $1/\sum_{j=1}^{N} f_j^2$ 로 정규화하여 정의한다.^[3]

: $S(\mathbf{q}) = \frac{1}{\sum_{j=1}^{N}f_j^2} \sum_{j=1}^N \sum_{k=1}^N f_j f_k \mathrm{e}^{-i \mathbf{q} \cdot (\mathbf{R}_j - \mathbf{R}_{k})}$

물질이 분말 또는 단순 액체와 같이 등방성인 경우, 강도는 $q=|\mathbf{q}|$ 및 $r_{jk} = |\mathbf{r}_j-\mathbf{r}_k|$ 에 따라 달라진다. 3차원에서 구조 인자는 다음과 같이 Debye 산란 방정식으로 단순화된다.^[1]

: $S(\mathbf{q}) = \frac{1}{\sum_{j=1}^N f_j^2} \sum_{j=1}^N \sum_{k=1}^N f_j f_k \frac{\sin(q r_{jk})}{q r_{jk}}$

결정에서 구성 입자는 주기적으로 배열되어 병진 대칭을 이루며, 격자를 형성한다. 결정 구조는 모든 격자점에 위치한 원자 그룹인 기저를 가진 브라베 격자로 설명할 수 있다. 즉, [결정 구조] = [격자] $\ast$ [기저]이다. 격자가 무한하고 완전히 규칙적이면 시스템은 완벽한 결정이다. 이러한 시스템의 경우, $\mathbf{q}$ 에 대한 특정 값 집합만이 산란을 제공할 수 있으며, 다른 모든 값에 대한 산란 진폭은 0이다. 이 값 집합은 실제 공간 결정 격자의 푸리에 변환인 역격자를 형성한다.

3. 1. 체심 입방체 (BCC)

체심 입방 구조(body-centered cubic^영어)는 기본 벡터

(a\hat{x}, a\hat{y}, a\hat{z})

와 기저

\mathbf{r}_0 = \vec{0}

,

\mathbf{r}_1 = \frac 1 2 a(\hat{x} + \hat{y} + \hat{z})

로 표현되는 단순한 입방 구조이다. 이에 상응하는 역격자 역시 한 변이

\frac{2\pi}a

인 단순 입방 구조이다.

단일원자 결정에서 모든 구조 인자

f

는 동일하다. 밀러 지수

(hkl)

로 표현되는, 기본 벡터

\mathbf{K}=\frac{2\pi}a(h\hat{x}^* + k\hat{y}^* + l\hat{z}^*)

로 나타내는 결정면에 대해 산란되는 입자의 휘도는 다음과 같다.

:

\begin{align}F_{\mathbf{K}}& = f \left[ e^{-i\mathbf{K}\cdot\vec{0}} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y} + \hat{z})} \right] \\& = f \left[ 1 + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y} + \hat{z})} \right] \\& = f \left[ 1 + e^{-i\pi(h + k + l)} \right]\\& = f \left[ 1 + (-1)^{h + k + l} \right] \\\end{align}

:(이 때,

e^{-i\pi}

은 오일러 항등식에 의해 (-1)이다.)

따라서 밀러 지수

(hkl)

인 면에서 산란될 때 구조 인자는 다음과 같다.

:

F_{hkl} =  \begin{cases}2f, & h + k + l = \mbox{even}\\0, & h + k + l  = \mbox{odd}\end{cases}

이 결과는 체심 구조 결정에서 산란 실험을 할 때 반사되는 입자를 관찰하려면 밀러 지수의 합이 짝수여야 함을 보여준다. 밀러 지수의 합이 짝수가 아니면 구조 인자가 0이 되는데, 이는 산란되는 입자의 파동이 상쇄 간섭을 일으킨다는 의미이다.

산란 각도가 증가하면(즉, 밀러 지수가 커지면) 구조 인자가 급격히 감소하므로, 체심 구조 결정에서 가장 강한 산란은 밀러 지수 (110)에서 나타난다. (110) 방향면은 체심 구조 결정에서 가장 밀도가 높은 방향이며, 결정을 박막으로 성장시킬 때 가장 적은 에너지가 필요하다. 따라서 철이나 텅스텐과 같은 체심 구조 박막은 (110) 방향성을 갖는 경향이 있다.

3. 2. 면심 입방체 (FCC)

단원자 면심 입방체(face-centered cubic^영어) 결정에서 기저를 결정하는 원자는 원점

\mathbf{r}_0 = \vec{0}

(밀러 지수 (0,0,0))과 세 면의 중심

\mathbf{r}_1 = (a/2)(\hat{x} + \hat{y})

,

\mathbf{r}_2 = (a/2)(\hat{y} + \hat{z})

,

\mathbf{r}_3 = (a/2)(\hat{x} + \hat{z})

(밀러 지수 (1/2,1/2,0), (0,1/2,1/2), (1/2,0,1/2))에 위치한다. 이에 따르면 산란되는 입자의 휘도는 다음과 같다.

:

\begin{matrix}F_{\mathbf{K}} & = & f \left[ e^{-i\mathbf{K}\cdot\vec{0}} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{y})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{y} + \hat{z})} + e^{-i\mathbf{K}\cdot(a/2)(\hat{x} + \hat{z})} \right] \\& = & f \left[ 1 + (-1)^{h + k} + (-1)^{k + l} + (-1)^{h + l} \right] \\\end{matrix}

구조 인자는 다음과 같다.

:

F_{hkl} =  \begin{cases} 4f, & h,k,l  \ \ \mbox{all even or all odd}\\0, & h,k,l \ \  \mbox{mixed parity} \end{cases}

FCC 격자는 브라베 격자이며, 이에 대한 푸리에 변환은 체심 입방 격자이다.

F_{hk\ell}

을 얻기 위해 각 격자점에 하나의 원자가 있는 FCC 결정을 기저가 4개 원자인 단순 입방 격자로 간주하면, 원점

x_j, y_j, z_j = (0, 0, 0)

과 세 개의 인접한 면 중심

x_j, y_j, z_j = \left(\frac{1}{2},\frac{1}{2},0\right)

,

\left(0,\frac{1}{2},\frac{1}{2}\right)

및

\left(\frac{1}{2},0,\frac{1}{2}\right)

에 위치한다. 식은 다음과 같이 표현된다.

:

F_{hk\ell} = f \sum_{j=1}^{4} \mathrm{e}^{[-2 \pi i (h x_j + k y_j + \ell z_j)]} = f \left[ 1 + \mathrm{e}^{[-i \pi (h + k)]}+ \mathrm{e}^{[-i \pi (k + \ell)]} + \mathrm{e}^{[-i \pi (h + \ell)]} \right]=  f \left[ 1 + (-1)^{h + k} + (-1)^{k + \ell} + (-1)^{h + \ell} \right]

결과는 다음과 같다.

:

F_{hk\ell} =  \begin{cases} 4f, & h,k,\ell  \ \ \mbox{모두 짝수 또는 모두 홀수}\\0, & h,k,\ell \ \  \mbox{패리티 혼합} \end{cases}

면심 구조 결정에서 산란 실험을 할 때, 가장 강한 산란 현상은 밀러 지수 (111) 방향에서 발생한다. 금과 같은 면심 구조 결정 물질은 (111) 방향에서 삼각 표면 대칭(triangular surface symmetry)으로 성장한다. FCC 구조로 결정화되는 물질의 가장 강한 회절 피크는 일반적으로 (111)이다. 회절 빔 그룹(

h,k,\ell

의 패리티 혼합)에 대한 0의 회절 강도를 체계적 부재라고 한다.

3. 3. 다이아몬드 구조체

다이아몬드, 대부분의 반도체, 주석 등은 다이아몬드 구조 결정이다. 기본 구조에는 8개의 원자가 다음 위치에 분포한다.

:

\begin{align}\mathbf{r}_0 &= \vec{0}\\\mathbf{r}_1 &= \frac 1 4 a(\hat{x} + \hat{y} + \hat{z})\\\mathbf{r}_2 &= \frac 1 4 a(2\hat{x} + 2\hat{y})\\\mathbf{r}_3 &= \frac 1 4 a(3\hat{x} + 3\hat{y} + \hat{z})\\\mathbf{r}_4 &= \frac 1 4 a(2\hat{x} + 2\hat{z})\\\mathbf{r}_5 &= \frac 1 4 a(2\hat{y} + 2\hat{z})\\\mathbf{r}_6 &= \frac 1 4 a(3\hat{x} + \hat{y} + 3\hat{z})\\\mathbf{r}_7 &= \frac 1 4 a(\hat{x} + 3\hat{y} + 3\hat{z})\\\end{align}

구조 인자는 다음과 같다.

:

\begin{align}F_{\mathbf{K}}& = f\begin{bmatrix}e^{-i\mathbf{K}\cdot\vec{0}} &+& e^{-i\mathbf{K}\cdot\frac 1 2 a(\hat{x} + \hat{y})} &+& e^{-i\mathbf{K}\cdot\frac 1 2 a(\hat{y} + \hat{z})} &+& e^{-i\mathbf{K}\cdot\frac 1 2 a(\hat{x} + \hat{z})} &+ \\e^{-i\mathbf{K}\cdot\frac 1 4 a(\hat{x} + \hat{y} + \hat{z})} &+&e^{-i\mathbf{K}\cdot\frac 1 4 a(3\hat{x} + \hat{y} + 3\hat{z})} &+&e^{-i\mathbf{K}\cdot\frac 1 4 a(3\hat{x} + 3\hat{y} + \hat{z})} &+&e^{-i\mathbf{K}\cdot\frac 1 4 a(\hat{x} + 3\hat{y} + 3\hat{z})}\end{bmatrix} \\& = f\begin{bmatrix}1 &+& (-1)^{h + k} &+& (-1)^{k + l} &+& (-1)^{h + l} &+ \\(-i)^{h + k + l} &+& (-i)^{3h + k + 3l} &+& (-i)^{3h + 3k + l} &+& (-i)^{h + 3k + 3l}\end{bmatrix} \\& = f \left[ 1 + (-1)^{h + k} + (-1)^{k + l} + (-1)^{h + l} \right] \cdot \left[ 1 + (-i)^{h + k + l} \right]\\\end{align}

이에 의하면, 밀러 지수

(h, k, l)

에 짝수와 홀수가 섞여 있으면, 구조 인자는 0 이 된다. 그렇지 않을 경우, 다음과 같다.

밀러 지수 $(h,k,l)$ 가 홀수이면 $F=4f(1 \pm i), \ FF^*=32f^2$
밀러 지수 $(h,k,l)$ 가 짝수이고 $h+k+l = 4n$ ( $n$ 는 0을 포함한 자연수)를 만족하면 $F = 8f$
밀러 지수 $(h,k,l)$ 가 짝수이고 $h+k+l \ne 4n$ ( $n$ 는 0을 포함한 자연수)이면 $F = 0$

다이아몬드 입방 결정 구조는 탄소(다이아몬드), 주석, 그리고 대부분의 반도체에서 나타난다. 입방 단위 세포에는 8개의 원자가 있고, 이 구조는 다음과 같은 위치에 있는 8개의 원자를 기본으로 하는 단순 입방으로 간주할 수 있다.

:

\begin{align} x_j, y_j, z_j  = &(0,\ 0,\ 0)   &\left(\frac{1}{2},\ \frac{1}{2},\ 0\right)\   &\left(0,\ \frac{1}{2},\ \frac{1}{2}\right)  &\left(\frac{1}{2},\ 0,\ \frac{1}{2}\right) \\   &\left(\frac{1}{4},\ \frac{1}{4},\ \frac{1}{4}\right) &\left(\frac{3}{4},\ \frac{3}{4},\ \frac{1}{4}\right)\  &\left(\frac{1}{4},\ \frac{3}{4},\ \frac{3}{4}\right) &\left(\frac{3}{4},\ \frac{1}{4},\ \frac{3}{4}\right)  \\\end{align}

이것을 면심 입방(FCC)과 비교하면 (0, 0, 0)과 (1/4, 1/4, 1/4)에 두 개의 원자를 기본으로 하는 FCC로 설명하는 것이 더 간단하다는 것을 알 수 있다. 이 기본에 대해, 방정식은 다음과 같다.

:

F_{hk\ell}(\rm{basis}) = f \sum_{j=1}^{2} \mathrm{e}^{[-2 \pi i (h x_j + k y_j + \ell z_j)]} = f \left[ 1 + \mathrm{e}^{[-i \pi/2 (h + k + \ell)]} \right] = f\left[ 1 + (-i)^{h + k + \ell} \right]

그리고 다이아몬드 입방 구조에 대한 구조 인자는 이것과 위의 FCC에 대한 구조 인자의 곱이다(원자 형태 인자는 한 번만 포함).

:

F _{hk\ell} =  f \left[ 1 + (-1)^{h + k} + (-1)^{k + \ell} + (-1)^{h + \ell} \right] \times \left[ 1 + (-i)^{h + k + \ell} \right]

결과는 다음과 같다.

h, k, ℓ이 혼합된 패리티(홀수와 짝수 값의 조합)인 경우 첫 번째(FCC) 항은 0이므로 $|F _{hk\ell}|^2 = 0$
h, k, ℓ이 모두 짝수이거나 모두 홀수인 경우 첫 번째(FCC) 항은 4이다.
h+k+ℓ이 홀수인 경우 $F _{hk\ell} =4f(1 \pm i), |F _{hk\ell}|^2 = 32f^2$
h+k+ℓ이 짝수이고 4로 정확히 나누어 떨어지는 경우( $h+k+\ell = 4n$ ) $F _{hk\ell} =4f\times 2, |F _{hk\ell}|^2 = 64f^2$
h+k+ℓ이 짝수이지만 4로 정확히 나누어 떨어지지 않는 경우( $h+k+\ell \neq 4n$ ) 두 번째 항은 0이고 $|F _{hk\ell}|^2 = 0$

이러한 점들은 다음 방정식에 의해 캡슐화된다.

:

F_{hk\ell}=\begin{cases}8f, & h+k+\ell=4N\\4(1\pm i)f, & h+k+\ell = 2N+1\\0, & h+k+\ell = 4N+2\\\end{cases}

:

\Rightarrow |F_{hk\ell}|^2=\begin{cases}64f^2, & h+k+\ell=4N\\32f^2, & h+k+\ell = 2N+1\\0, & h+k+\ell = 4N+2\\\end{cases}

여기서

N

은 정수이다.

3. 4. 섬아연석 구조 (Zincblende)

섬아연석 구조는 모든 원소가 동일한 다이아몬드 구조와 유사하지만, 두 개의 서로 다른 면심 입방 격자가 서로 관통하는 화합물이라는 점이 다르다. 화합물의 두 원소를

A

와

B

로 표시하면, 구조 인자는 다음과 같다.

:

F_{hk\ell}=\begin{cases}4(f_A+f_B), & h+k+\ell=4N\\4(f_A \pm if_B), & h+k+\ell = 2N+1\\4(f_A-f_B), & h+k+\ell = 4N+2\\\end{cases}

3. 5. 염화 세슘 (Cesium chloride)

염화 세슘은 Cs가 (0,0,0)에 있고 Cl이 (1/2, 1/2, 1/2)에 있는 기저를 가진 단순 입방 결정 격자이다(또는 그 반대도 상관없다). 구조 인자(

F_{hk\ell}

)는 다음과 같이 표현된다.

:

F_{hk\ell} = \sum_{j=1}^{2} f_j \mathrm{e}^{[-2 \pi i (h x_j + k y_j + \ell z_j)]} =  \left[ f_{Cs} + f_{Cl} \mathrm{e}^{[-i \pi (h + k+\ell)]}\right] =  \left[ f_{Cs} + f_{Cl}(-1)^{h + k + \ell} \right]

여기서

f_{Cs}

와

f_{Cl}

는 각각 세슘과 염소의 원자 폼 인자(atomic form factor)이며,

(h, k, \ell)

은 밀러 지수이다.

평면

(hk\ell)

에서의 산란에 대한 구조 인자는 다음과 같다.

:

F_{hk\ell} =  \begin{cases} (f_{Cs} + f_{Cl}), & h + k + \ell & \text{짝수}\\(f_{Cs} - f_{Cl}), & h + k + \ell & \text{홀수} \end{cases}

이에 따라 산란 강도

(|F_{hk\ell}|^2)

는 다음과 같이 주어진다.

:

|F_{hk\ell}|^2 =  \begin{cases} (f_{Cs} + f_{Cl})^2, & h + k + \ell & \text{짝수}\\(f_{Cs} - f_{Cl})^2, & h + k + \ell & \text{홀수} \end{cases}

즉, 밀러 지수의 합(

h + k + \ell

)이 짝수일 때는

(f_{Cs} + f_{Cl})^2

, 홀수일 때는

(f_{Cs} - f_{Cl})^2

의 산란 강도를 가진다.

3. 6. 육방 밀집 구조 (HCP)

흑연에서 두 좌표는 원점

\left(0,0,0 \right)

과 ''c'' 축 위로 다음 평면인 ''c''/2에 위치하며, 따라서

\left(1/3,2/3,1/2 \right)

를 포함한다. 이는 다음과 같다.

:

F_{hk\ell} = f\left[1 +  e^{2\pi i \left(\tfrac{h}{3} + \tfrac{2k}{3} + \tfrac{\ell}{2} \right)} \right]

여기에서 허수 변수

X \equiv h/3 + 2k/3 + \ell /2

를 정의하는 것이 편리하며, 제곱된 절댓값을 고려하면 다음과 같다.

:

|F|^2 = f^2\left(1+e^{2\pi i X}\right)\left(1+e^{-2\pi i X}\right)= f^2\left(  2 +e^{2\pi i X} +e^{-2\pi i X} \right)= f^2\left( 2 + 2\cos[2\pi X] \right) = f^2\left( 4\cos^2 \left[\pi X \right] \right)

이로부터 구조 인자에 대한 다음 조건을 얻을 수 있다.

:

|F_{hk\ell}|^2 =\begin{cases}0, & h+2k=3N\text{ and }\ell \text{ is odd,}\\4f^2, & h+2k=3N\text{ and }\ell \text{ is even,}\\3f^2, & h+2k=3N\pm 1\text{ and }\ell \text{ is odd,}\\f^2, & h+2k=3N\pm 1\text{ and }\ell \text{ is even}\\\end{cases}

4. 완전 결정 및 불완전 결정

결정에서 구성 입자가 주기적으로 배열되어 병진 대칭을 이루며 격자를 형성할 때, 이 시스템은 완벽한 결정이라고 불린다. 완벽한 결정의 경우, 특정 값의 산란 벡터( $\mathbf{q}$ )에서만 산란이 발생하며, 다른 값에서는 산란 진폭이 0이 된다. 이러한 산란 가능한 값의 집합은 실제 공간 결정 격자의 푸리에 변환인 역격자를 형성한다.

원칙적으로 산란 인자 $S(\mathbf{q})$ 는 완벽한 결정의 산란을 결정하는 데 사용될 수 있다. 기저가 원점에 있는 단일 원자이고 모든 원자가 동일한 환경을 갖는 간단한 경우, 구조 인자는 격자의 푸리에 변환의 제곱된 절대값으로 표현되며, 산란이 0이 아닌 강도를 가질 수 있는 방향을 보여준다. 이러한 $\mathbf{q}$ 값에서 모든 격자점의 파동은 위상이 일치한다. 구조 인자의 값은 모든 역격자점에서 동일하며, 강도는 원자 폼 팩터( $f$ )가 $\mathbf{q}$ 에 따라 변화하는 것에 의해서만 달라진다.^[4]

결정학에서 기저와 격자는 별도로 취급된다. 완벽한 결정의 경우, 격자는 역격자를 제공하여 회절 빔의 위치(각도)를 결정하고, 기저는 구조 인자 $F_{hkl}$ 을 제공하여 회절 빔의 진폭과 위상을 결정한다.

: $F_{hk\ell} = \sum_{j=1}^N f_j \mathrm{e}^{[-2 \pi i (h x_j + k y_j + \ell z_j)]}$

여기서 합은 단위 세포 내의 모든 원자에 대한 것이고, $x_j, y_j, z_j$ 는 $j$ 번째 원자의 위치 좌표이며, $f_j$ 는 $j$ 번째 원자의 산란 인자이다. $(hkl)$ 은 밀러 지수로 정의된 실제 공간 평면에 해당하는 역격자 점을 정의한다.

$F_{hk\ell}$ 는 단위 세포 내의 모든 원자로부터의 파동의 벡터 합이다. 임의의 격자점에 있는 원자는 모든 $hk\ell$ 에 대해 기준 위상각 0을 갖는다.

하지만 실제 결정은 유한한 크기를 가지며, 그 질서에 불완전성을 나타낸다. 이러한 불완전성은 재료의 특성에 큰 영향을 미칠 수 있다. 앙드레 기니에는 결정의 장거리 질서를 보존하는 불완전성을 '제1종 무질서', 이를 파괴하는 불완전성을 '제2종 무질서'로 구분했다.^[5] 제1종 무질서의 예로는 열 진동이 있고, 제2종 무질서의 예로는 전위가 있다.

4. 1. 1차원 및 2차원 완전 결정

결정에서 구성 입자는 주기적으로 배열되어 병진 대칭을 이루며, 격자를 형성한다. 1차원 및 2차원 결정에서 역격자는 다음과 같이 구성된다. 주기

a

를 갖는 선 위의 입자의 경우 (1차원), 역격자는 간격이

2\pi/a

인 무한 배열의 점이다. 2차원에는 단 5개의 브라베 격자가 있으며, 해당 역격자는 직접 격자와 동일한 대칭성을 갖는다.

2차원에서 결정 구조 인자는

F_{hk} = \sum_{j=1}^N f_j \mathrm{e}^{[-2 \pi i (h x_j + k y_j)]}

로 정의할 수 있다.

그래핀과 같은 실제 2차원 결정은 3차원 공간에 존재한다.

xy

평면에 존재하는 3차원 공간의 2차원 육각형 시트의 역격자는

z

또는

z^*

축에 평행하고

\pm \infty

로 확장되며, 일정한

z

평면을 육각형 점 배열로 교차하는 선의 육각형 배열이다.

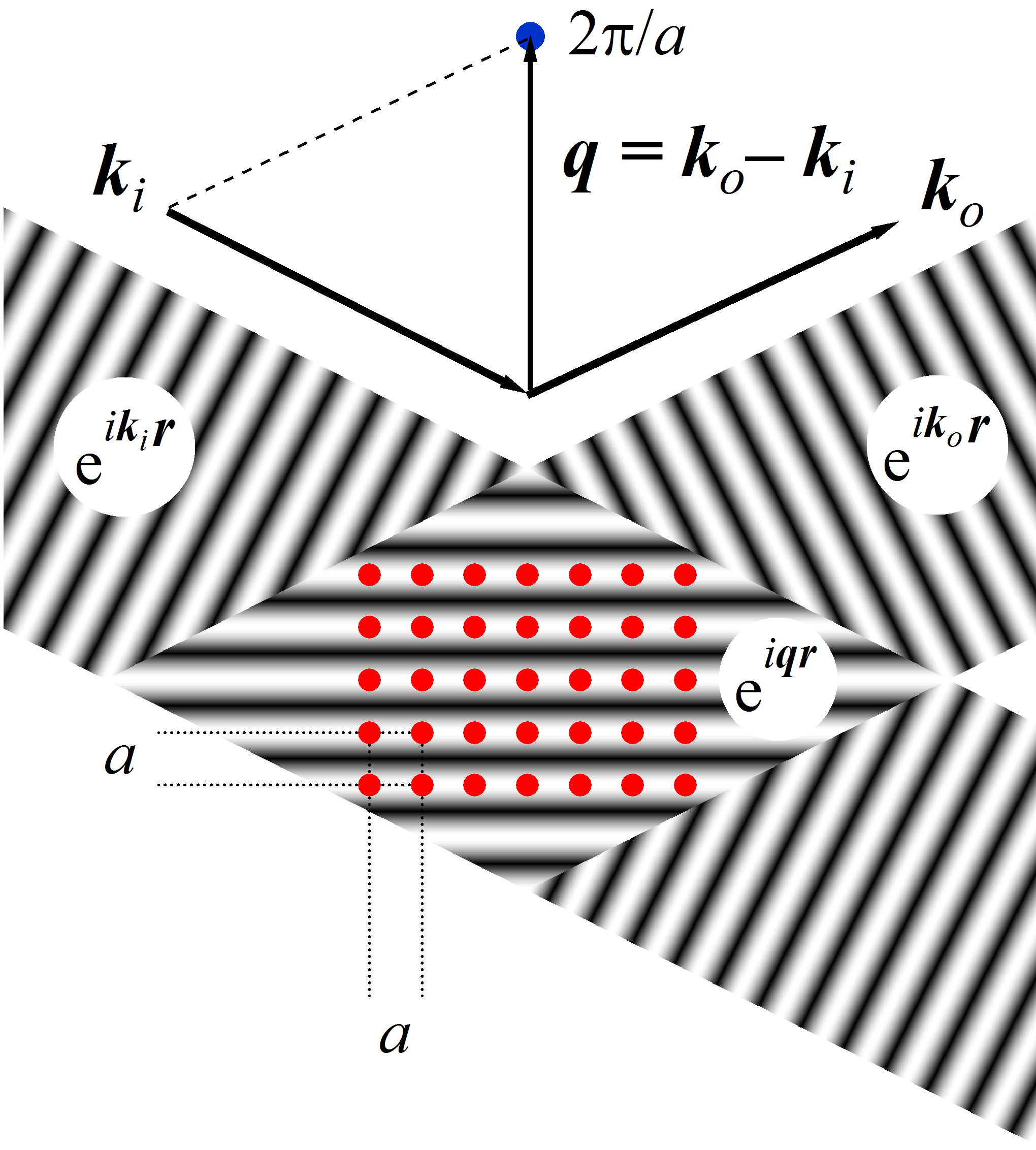
정사각형(평면) 격자에 의한 산란 다이어그램. 입사 및 출사 빔과 파동 벡터 $\mathbf{k}_i$ , $\mathbf{k}_o$ 및 산란 벡터 $\mathbf{q}$ 사이의 관계를 보여준다.

위 그림은 2차원 역격자의 한 벡터 구성과 산란 실험과의 관계를 보여준다. 파동 벡터

\mathbf{k}_i

를 갖는 평행 빔이 매개변수

a

인 정사각형 격자에 입사한다. 산란된 파동은 특정 각도에서 감지되며, 이는 출사 빔의 파동 벡터

\mathbf{k}_o

를 정의한다 (탄성 산란의 가정 하에

|\mathbf{k}_o| = |\mathbf{k}_i|

). 산란 벡터

\mathbf{q}=\mathbf{k}_o - \mathbf{k}_i

를 동일하게 정의하고 조화 패턴

\exp (i \mathbf{q}\mathbf{r})

을 구성할 수 있다. 그림에서 이 패턴의 간격은 입자 행 사이의 거리와 일치한다:

q = 2\pi /a

, 따라서 모든 입자의 산란에 대한 기여가 위상(보강 간섭)에 있다. 따라서 방향

\mathbf{k}_o

에서의 총 신호는 강하고

\mathbf{q}

는 역격자에 속한다. 이 구성이 브래그 법칙을 충족한다는 것을 쉽게 알 수 있다.

4. 2. 유한 크기 효과

유한한 결정에서 구조 인자 $S(q)$를 계산할 때는 유한한 수의 원자($N$)를 고려해야 한다. 이러한 유한 크기 효과는 1차원 격자점을 예로 들어 설명할 수 있다. 위상 인자의 합은 기하 급수로 나타낼 수 있으며, 구조 인자는 다음과 같이 표현된다.

:$S(q) = \frac{1}{N} \left | \frac{1 - \mathrm{e}^{-i N q a}}{1 - \mathrm{e}^{-i q a}} \right |^2 = \frac{1}{N} \left [ \frac{\sin(N q a/2)}{\sin(q a/2)} \right ]^2.$

여기서 $q$는 산란 벡터이고, $a$는 격자 상수이다. 이 함수는 $N$ 값에 따라 변화하는 형태를 보인다.

모든 입자로부터의 산란이 동위상(in-phase)일 때, 즉 산란이 역격자점 $q = 2 k \pi/a$ ($k$는 정수)일 때, 진폭의 합은 $N$에 비례하고, 따라서 강도의 최댓값은 $N^2$에 비례한다. 로피탈의 정리를 사용하여 $S(q \to 0)$의 극한을 구하면 $S(q = 2 k \pi/a) = N$임을 알 수 있다. 중간점에서는 $S(q = (2 k +1) \pi/a) = 1/N$이며, 피크의 너비는 $1/N$에 비례하여 감소한다.

$N$이 매우 큰 경우, 피크는 완벽한 1차원 격자의 역격자, 즉 무한히 날카로운 디랙 델타 함수가 된다. 결정학에서 $F_{hkl}$이 사용될 때, $N$은 충분히 크다고 가정하며, 회절에 대한 형식적인 크기 효과는 $\left [ \frac{\sin(N q a/2)}{(q a/2)} \right ]^2$로 간주된다. 이는 역격자점 $q \approx 2 k \pi/a$ 근처의 $S(q)$ 표현식과 동일하다.

유한한 실제 결정 구조는 격자와 기저의 컨볼루션에 사각형 함수(결정 내부에서 1, 외부에서 0의 값을 갖는 함수)를 곱한 것으로 설명할 수 있다. 그러면 $\mathcal{F}$[결정 구조] = $\mathcal{F}$[격자] $\times \mathcal{F}$[기저] $\ast {F}$[사각형 함수]가 된다. 즉, 산란은 [역격자] $\times$ [구조 인자] $\ast$ sinc 함수에 비례한다.

따라서 완전한 결정의 경우 위치의 델타 함수인 강도는 각 점 주위의 $\operatorname{sinc}^2$ 함수가 되어, 최댓값은 $N^2$에 비례하고, 너비는 $1/N$에 비례하며, 면적은 $N$에 비례한다.

4. 3. 제1종 무질서

결정 내 무질서에 대한 이 모델은 완전 결정의 구조 인자에서 시작한다. 간단하게 1차원에서, 그리고 ''N''개의 면을 사용하여, 완전한 유한 격자에 대한 위의 표현식에서 시작한 다음, 이 무질서는 단지 곱셈 인자에 의해

S(q)

를 변경하여 다음을 제공한다.^[1]

:

S(q) = \frac{1}{N} \left [ \frac{\sin(N q a/2)}{\sin(q a/2)} \right ]^2 \exp\left(-q^2\langle \delta x^2\rangle\right)

여기서 무질서는 완벽한 1차원 격자 내 위치

x_j

의 평균 제곱 변위로 측정된다. (

a (j - (N-1)/2)

, 즉,

x_j=a (j - (N-1)/2) +\delta x

). 여기서

\delta x

는 작고 (

a

보다 훨씬 작음) 무작위 변위이다. 제1종 무질서의 경우, 각 무작위 변위

\delta x

는 다른 변위와 독립적이며, 완벽한 격자에 대해 독립적이다. 따라서 변위

\delta x

는 결정의 병진 질서를 파괴하지 않는다. 이는 무한 결정(

N\to\infty

)의 경우 구조 인자가 여전히 델타 함수 브래그 피크를 갖는다는 결과를 초래한다. 즉, 피크 폭은 이 종류의 무질서로 인해 여전히

N\to\infty

로 갈 때 0으로 간다. 그러나 피크의 진폭을 감소시키며, 지수 인자에

q^2

의 인자가 있기 때문에, 작은

q

에서의 피크보다 큰

q

에서의 피크를 훨씬 더 많이 감소시킨다.

구조는 단순히

q

와 무질서에 의존하는 항에 의해 감소된다. 제1종 무질서는 산란 평면을 흐리게 하여 효과적으로 형태 인자를 감소시키기 때문이다.

3차원에서도 효과는 동일하며, 구조는 다시 곱셈 인자에 의해 감소되며, 이 인자는 종종 드바이-월러 인자라고 불린다. 드바이-월러 인자는 종종 열적 운동, 즉

\delta x

가 열적 운동에 기인한다고 여겨지지만, 열적 운동뿐만 아니라 완벽한 격자에 대한 모든 무작위 변위가 드바이-월러 인자에 기여한다는 점에 유의해야 한다.

4. 4. 제2종 무질서

원자 쌍 사이의 상관 관계는 거리가 증가함에 따라 감소하는 경향이 있는데, 이러한 요동은 결정의 구조 인자에서 브래그 봉우리를 넓게 만든다. 이러한 현상을 이해하기 위해 평균 간격

a

를 가진 판 스택으로 구성된 1차원 모델을 고려한다.^[6] 이 모델은 호제만과 그의 동료들이 개발하여 여러 재료에 적용하였다.^[7]

기니에와 호제만은 이러한 종류의 무질서를 제2종 무질서라고 칭했고, 특히 호제만은 이러한 불완전한 결정 정렬을 파라결정 정렬이라고 불렀다. 이와 대조적으로, 제1종 무질서는 드바이-월러 인자를 유발한다.

1차원 모델에서 구조 인자 S(q)는 다음과 같이 정의된다.

:

S(q) = \frac{1}{N} \sum_{j,k=1}^N \mathrm{e}^{-i q(x_j-x_k)}

무한 결정(

N\to\infty

)의 경우, 격자 사이트 쌍을 고려하여 위 식을 다음과 같이 다시 쓸 수 있다.

:

S(q) = 1+ 2 \sum_{m=1}^{\infty}\int_{-\infty}^{\infty}{\rm d}(\Delta x)p_m(\Delta x)\cos\left(q\Delta x\right)

여기서

p_m(\Delta x)

는

m

격자 간격만큼 떨어진 평면 쌍의 간격

\Delta x

에 대한 확률 밀도 함수이다. 인접 평면 간격의 요동이 가우시안 분포를 따른다고 가정하면,

:

p_1(\Delta x)=\frac{1}{\left(2\pi\sigma_2^2\right)^{1/2}}\exp\left[-\left(\Delta x-a\right)^2/(2\sigma_2^2)\right]

이고,

p_m(\Delta x)

는 다음과 같이 주어진다.

:

p_m(\Delta x)=\frac{1}{\left(2\pi m\sigma_2^2\right)^{1/2}}\exp\left[-\left(\Delta x-ma\right)^2/(2m\sigma_2^2)\right]

이를 이용하여 구조 인자를 계산하면,

:

S(q)=\frac{1-r^2}{1+r^2-2r\cos(qa)}

(

r=\exp[-q^2\sigma_2^2/2]

)

이 함수는

q_p=2n\pi/a

에서 봉우리를 가지며, 봉우리 높이는 다음과 같다.

:

S(q_P)=\frac{1+r}{1-r}\approx\frac{4}{q_P^2\sigma_2^2}=\frac{a^2}{n^2\pi^2\sigma_2^2}

즉, 연속적인 봉우리의 높이는 봉우리 순서의 제곱에 반비례하여 감소한다. 이는 무질서가 봉우리 높이를 낮추는 효과를 나타낸다.

q\sigma_2\ll 1

의 한계에서, 봉우리 근처의 구조 인자는 로렌츠 또는 코시 함수 형태로 근사할 수 있다.

:

S(q)\approx\frac{S(q_P)}{1+\frac{r}{(1-r)^2}\frac{\Delta q^2a^2}{2}}\approx \frac{S(q_P)}{1+\frac{\Delta q^2}{[q_P^2\sigma_2^2/a]^2/2}}

이 함수의 반치전폭(FWHM)은

q_P^2\sigma_2^2/a=4\pi^2n^2(\sigma_2/a)^2/a

이며, 봉우리 순서의 제곱에 비례하여 증가한다.

봉우리 높이와 FWHM의 곱은

4/a

로 일정하며, 이는

q\sigma_2\ll 1

또는

\sigma_2/a\ll 1

(약한 무질서) 조건에서 성립한다.

크기가

N

인 유한한 1차원 결정의 경우, 구조 인자는 다음과 같이 주어진다.

:

S(q)=1+2\sum_{m=1}^N\left(1-\frac{m}{N}\right)r^m\cos\left(mqa\right)

5. 액체의 구조 인자

액체는 장거리 질서가 없어 결정과 달리 구조 인자에 날카로운 피크가 나타나지 않는다. 그러나 밀도와 입자 간 상호작용에 따라 어느 정도의 단거리 질서를 보인다. 액체는 등방성을 가지므로 구조 인자는 산란 벡터의 크기 $q = \left |\mathbf{q} \right |$ 에만 의존한다.^[8]

방사형 분포 함수 $g(r)$ 을 사용하여 구조 인자 $S(q)$ 를 다음과 같이 표현할 수 있다.

: $S(q) = 1 + \rho \int_V \mathrm{d} \mathbf{r} \, \mathrm{e}^{-i \mathbf{q}\mathbf{r}} g(r)$ .

이상 기체: 상호작용이 없는 극한의 경우, 구조 인자는 $S(q) = 1$ 로 나타난다. 이는 서로 다른 입자의 위치 사이에 상관관계가 없기 때문이다.

강체 구(hard-sphere) 액체: 하드 스피어 모델에서 입자는 반경 $R$ 의 침투 불가능한 구체로 묘사된다. 중심 간 거리가 $r \geq 2R$ 일 때만 상호작용이 존재한다. 이 모델은 퍼커스–예빅 근사에서 해석적 해를 가지며,^[9] 액체 금속^[10] 및 콜로이드 현탁액^[11] 등 다양한 시스템을 잘 설명한다.

퍼커스-예빅 근사를 사용하여 계산된 하드-스피어 유체의 구조 인자, 부피 분율 $\Phi$ 는 1%에서 40%까지

고분자 시스템: 고분자 시스템에서 구조 인자는 입자 위치 간의 상관관계를 측정하며, 동일 사슬 또는 다른 사슬에 속하는 단량체에 따라 상관관계가 다르게 나타난다. 단일 사슬 구조 인자 $S_1 (q)$ 를 사용하여 나타낼 수 있다.

참조

_[1] 서적 X-ray Diffraction https://archive.org/[...] Addison Wesley 1969
_[2] 서적 Electron Diffraction Techniques Vol 1 Oxford Science 1992
_[3] 서적 Underneath the Bragg Peaks: Structural Analysis of Complex Material Elsevier 2012
_[4] 웹사이트 Structure Factor http://reference.iuc[...] IUCr 2016-09-15
_[5] 문서 See Guinier, chapters 6-9
_[6] 서적 X-Ray Diffraction WH Freeman
_[7] 논문 Application of the Theory of Paracrystals to the Crystal Structure Analysis of Polyacrylonitrile http://scitation.aip[...] 1963
_[8] 문서 See Chandler, section 7.5.
_[9] 논문 Exact Solution of the Percus-Yevick Integral Equation for Hard Spheres
_[10] 논문 Structure and Resistivity of Liquid Metals
_[11] 논문 Phase behaviour of concentrated suspensions of nearly hard colloidal spheres
_[12] 문서 See Teraoka, Section 2.4.4.

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com