다각진
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
다각진(Magic polygon)은 둘레에 정수를 배치하여 각 변의 수의 합이 마법 상수가 되도록 하는 수의 배치이다. 마법진의 일반화된 형태로, 마법 삼각형이 다각진의 예시에 해당한다. 다각진은 중심점이 있는 다각진, 축퇴된 다각진 등으로 분류되며, 빅토리아 야키치치와 라셸 부샤, 다니엘 디아스 아우구스토와 조시마르 다 실바 등에 의해 연구되었다.
더 읽어볼만한 페이지
- 마법진 - 별진
별진은 칠각별진, 팔각별진, 육각별진 등 다양한 종류의 별 모양 다각형을 포괄하는 용어로, 수학적 특징을 가지며 예술, 디자인, 교육 등 다양한 분야에서 응용 및 활용되는 잠재력을 지닌다. - 마법진 - 지수귀문도
- 마방진 - 멜랑콜리아 I
알브레히트 뒤러의 동판화 "멜랑콜리아 I"은 우울을 의인화한 인물과 여러 상징적 오브제를 통해 멜랑콜리아의 복합적인 의미와 예술가의 고뇌, 천재성을 탐구하는 작품이다. - 마방진 - 범마방진
범마방진은 가로, 세로, 대각선뿐 아니라 꺾인 대각선의 숫자 합도 동일한 마방진으로, 행이나 열을 이동시켜도 성질이 유지되며 특정 형태는 존재하지 않고 보조 방진이나 라틴 방진으로 생성 가능하며 동아시아에서 발전하여 현대 수학 및 다양한 분야에 응용된다.
| 다각진 | |
|---|---|
| 개요 | |
| 종류 | 도형 |
| 정의 | 평면 위에 직선으로 둘러싸인 다각형 |
| 특징 | 각 변의 길이와 각의 크기가 모두 같은 다각형 |
| 명칭 | |
| 어원 | '다각진(多角-)': 많은 각을 가진 도형이라는 의미의 한국어 명칭 |
| 영어 명칭 | Polygon (폴리곤) |
| 어원 설명 | 그리스어 'πολύς' (polús, "많은")와 'γωνία' (gōnía, "각")의 합성어 |
| 분류 | |
| 변의 수 | 삼각형, 사각형, 오각형 등 변의 수에 따라 분류 |
| 볼록성 | 볼록다각형, 오목다각형 |
| 정규성 | 정다각형, 비정다각형 |
| 성질 | |
| 내각의 합 | (n-2) × 180° (n은 변의 수) |
| 외각의 합 | 360° |
| 넓이 | 다각형의 종류와 변의 길이에 따라 계산 방법이 다름 |
| 활용 | |
| 건축 | 다양한 형태의 건물 설계에 활용 |
| 디자인 | 패턴, 로고 등 다양한 디자인 요소로 활용 |
| 수학 | 기하학적 성질 연구의 기본 대상 |
2. 둘레 다각진
'''다각진'''(多角陣, magic polygon영어) 또는 '''둘레 다각진'''(- 多角陣, perimeter magic polygon영어)은 둘레에 정수를 적어넣어, 한 모서리의 수의 합이 마법 상수가 되는 수의 배치이다.[9][10][11][12] 다각진은 삼각진 등이 있으며,[13] 마법진의 일반화이다.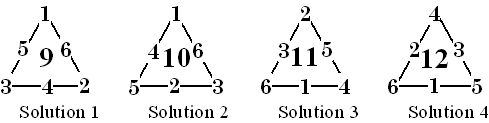
2. 1. 예시
다각진의 예시로는 마법 삼각형이 있으며, 이는 가장 간단한 형태의 둘레 다각진 중 하나이다. 마법 삼각형은 각 변의 정수 합이 모두 마법 상수가 되는 다각형으로, 마법 삼각형과 같은 다른 마법 도형의 일반화이다.[1][5][6]3. 중심점이 있는 다각진
Victoria Jakicic과 Rachelle Bouchat은 2''n''+1개의 점을 가진 ''n''각형에 중심을 지나는 n개의 선을 그은 다각진을 만들었다. 정가운데 수는 n+1이어야 하며 홀수각진은 없다.[14]
Danniel Dias Augusto과 Josimar da Silva 은 다각진 P(''n'',''k'')를 개의 동심 ''n''각형과 중심점으로 정의했다. 그들의 정의에서 Victoria Jakicic과 Rachelle Bouchat의 다각진은 P(''n'',2) 다각진으로 볼 수 있다. 또한 축퇴된 다각진도 정의하였다.[15]
Victoria Jakicic영어와 Rachelle Bouchat영어는 마법 다각형을 세 노드의 합이 같은 2''n''+1개의 노드를 가진 ''n''변 정다각형으로 정의했다. 그들의 정의에 따르면 3×3 마법 정사각은 마법 사각뿔로 볼 수 있다. 이 정의에 따르면 마법 홀수 각뿔은 없다.[7]
3. 1. 특징
Victoria Jakicic과 Rachelle Bouchat은 2''n''+1개의 점을 가진 ''n''각형에 중심을 지나는 n개의 선을 그은 다각진을 만들었다. 정가운데 수는 n+1이어야 하며 홀수각진은 없다.[14]Danniel Dias Augusto과 Josimar da Silva 은 다각진 P(''n'',''k'')를 ''k/2'' 개의 동심 ''n''각형과 중심점으로 정의했다. 그들의 정의에서 Victoria Jakicic과 Rachelle Bouchat의 다각진은 P(''n'',2) 다각진으로 볼 수 있다. 또한 축퇴된 다각진도 정의하였다.[15]
빅토리아 야키치치(Victoria Jakicic)와 라셸 부샤(Rachelle Bouchat)는 마법 다각형을 세 노드의 합이 같은 2''n''+1개의 노드를 가진 ''n''변 정다각형으로 정의했다. 그들의 정의에 따르면 3×3 마법 정사각은 마법 사각뿔로 볼 수 있다. 이 정의에 따르면 마법 홀수 각뿔은 없다.[7]
4. 축퇴된 다각진
Victoria Jakicic과 Rachelle Bouchat은 2''n''+1개의 점을 가진 ''n''각형에 중심을 지나는 n개의 선을 그은 다각진을 만들었다. 정가운데 수가 n+1이어야 하며 홀수각진은 없다.[14]
Danniel Dias Augusto과 Josimar da Silva는 다각진 P(''n'',''k'')를 개의 동심 ''n''각형과 중심점으로 정의했다. 그들의 정의에서 Victoria Jakicic과 Rachelle Bouchat의 다각진은 P(''n'',2) 다각진으로 볼 수 있다. 또한 축퇴된 다각진도 정의하였다.[15][8]
5. 다각진 연구
빅토리아 야키치치(Victoria Jakicic)와 라셸 부샤(Rachelle Bouchat)는 2''n''+1개의 점을 가진 ''n''각형에 중심을 지나는 n개의 선을 그은 다각진을 연구했다. 정가운데 수는 n+1이어야 하며 홀수각진은 없다.[14]
다니엘 디아스 아우구스토(Danniel Dias Augusto)와 조시마르 다 실바(Josimar da Silva)는 다각진 P(''n'',''k'')를 개의 동심 ''n''각형과 중심점으로 정의하여 연구를 확장했다. 그들의 정의에서 야키치치와 부샤의 다각진은 P(''n'',2) 다각진으로 볼 수 있다. 또한 축퇴된 다각진도 정의하였다.[15]
6. 기타
6. 1. 조합론적 관점
6. 2. 정수론적 관점
참조
[1]
웹사이트
Perimeter Magic Polygons
https://web.archive.[...]
2017-02-12
[2]
웹사이트
Perimeter Magic Polygon >k=3
http://www.magic-squ[...]
2017-02-12
[3]
서적
Math Skills: Arithmetic with Introductory Algebra and Geometry
https://archive.org/[...]
Kendall Hunt
2003-05-01
[4]
서적
Even More Mathematical Activities
https://books.google[...]
Cambridge University Press
1987-04-09
[5]
서적
Unsolved Problems in Geometry: Unsolved Problems in Intuitive Mathematics
https://books.google[...]
Springer Science & Business Media
2012-12-06
[6]
웹사이트
Perimeter Magic Triangles
http://recmath.org/M[...]
2017-02-12
[7]
ArXiv
Magic Polygons and Their Properties
[8]
ArXiv
Magic Polygons and Degenerated Magic Polygons: Characterization and Properties
[9]
웹인용
Perimeter Maghic Polygons
https://web.archive.[...]
2017-02-12
[10]
웹인용
Perimeter Magic Polygon >k=3
https://web.archive.[...]
2017-02-12
[11]
서적
Math Skills: Arithmetic with Introductory Algebra and Geometry
https://archive.org/[...]
Kendall Hunt
2003-05-01
[12]
서적
Even More Mathematical Activities
https://books.google[...]
Cambridge University Press
1987-04-09
[13]
웹인용
Perimeter Magic Triagonals
http://recmath.org/M[...]
2017-02-12
[14]
ArXiv
Magic Polygons and Their Properties
[15]
ArXiv
Magic Polygons and Degenerated Magic Polygons: Characterization and Properties
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com