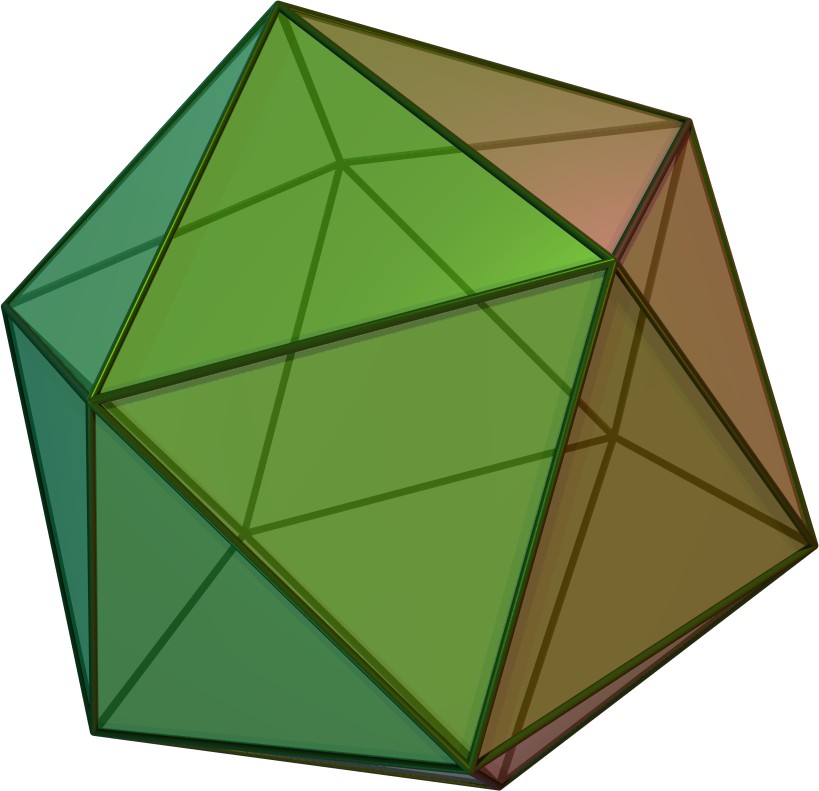
다듬은 정십이면체

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 성질
3. 데카르트 좌표
4. 관련 다면체 및 타일링
5. 깎은 정십이면체 그래프
참조

1. 개요

깎은 정십이면체는 12개의 정오각형 면과 80개의 정삼각형 면으로 이루어진 아르키메데스 다면체이다. 이 다면체는 정십이면체의 오각형 면을 확장하여 만들 수 있으며, 깎은 이십이십면체에서 교대 과정을 통해 파생될 수도 있다. 깎은 정십이면체는 겉넓이, 부피, 외접구 반지름에 대한 공식을 가지며, 삼각형 면과 오각형 면을 중심으로 하는 두 가지 직교 투영을 갖는다. 또한, 깎은 정십이면체 그래프는 다듬은 정십이면체의 꼭짓점과 모서리를 나타내는 그래프로, 60개의 꼭짓점과 150개의 모서리를 가지는 해밀턴 그래프이다.

더 읽어볼만한 페이지

아르키메데스의 다면체 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다.
아르키메데스의 다면체 - 깎은 정이십면체
깎은 정이십면체는 정이십면체의 꼭짓점을 잘라낸 아르키메데스의 다면체로, 32개의 면, 90개의 변, 60개의 꼭짓점을 가지며, 축구공, 풀러렌 분자 등 다양한 분야에서 활용된다.
평면 그래프 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다.
평면 그래프 - 정이십면체
정이십면체는 20개의 정삼각형 면으로 이루어진 볼록 정다면체로, 정반오각기둥 양쪽에 정오각뿔을 붙인 형태이며, 정십이면체와 쌍대 관계를 가지고 다양한 분야에서 활용된다.

다듬은 정십이면체
명칭
한국어 명칭	다듬은 정십이면체
영어 명칭	스너브 도데카헤드론 (snub dodecahedron)
다른 영어 명칭	스너브 아이코시도데카헤드론 (snub icosidodecahedron)
일본어 명칭	변형십이면체 (変形十二面体)
기하학적 성질
종류	반정다면체
면의 수	92
면의 종류	정삼각형: 80개 (20+60) 정오각형: 12개
변의 수	150
꼭짓점의 수	60
꼭짓점 구성	3.3.3.3.5 (정삼각형 4개, 정오각형 1개)
슈레플리 기호	sr{5, 3}
위소프 기호	\| 2 3 5
대칭군	I
쌍대다면체	오각육십면체
성질	볼록 다면체, 키랄성
시각적 표현
다듬은 정십이면체
다듬은 정십이면체 회전
다듬은 정십이면체 꼭짓점 도형
다듬은 정십이면체 전개도

2. 성질

깎은 정십이면체는 12개의 정오각형 면과 80개의 정삼각형 면으로 이루어져 있으며, 총 92개의 면을 가진다. 모든 아르키메데스 다면체 중에서 가장 높은 구형도(약 0.947)를 가진다.^[1] 꼬임각은 13.1064033769358이다. 준정다면체 중에서 가장 많은 면을 가지지만, 변과 꼭짓점의 수로는 능깎이 큰 이십면체가 최대이다.

한 변의 길이를 ''a''라고 할 때 겉넓이와 외접구의 반지름은 다음과 같다.

'''겉넓이''': $(20\sqrt{3}+3\sqrt{25+10\sqrt{5}})a^2$
'''외접구 반지름''': $\frac{a}{12}\sqrt{6\left(27+7\sqrt{5}+\sqrt[3]{20448+9140\sqrt{5}-12\sqrt{7137+3192\sqrt{5}}}+\sqrt[3]{20448+9140\sqrt{5}+12\sqrt{7137+3192\sqrt{5}}}\right)}$

2. 1. 기하학적 관계

다듬은 정십이면체는 정십이면체의 열두 오각형 면을 서로 닿지 않도록 바깥쪽으로 당겨 만들 수 있다. 적절한 거리에서 분할된 변 사이에 사각형 면을 채우고, 분할된 꼭짓점 사이에 삼각형 면을 채우면 롬비이십면체를 만들 수 있다. 그러나 다듬은 정십이면체의 경우, 오각형 면을 약간 덜 당기고 삼각형 면만 추가하여 다른 간격은 비워둔다. 그런 다음 오각형과 삼각형의 중심에 동일한 회전을 적용하여 간격이 두 개의 정삼각형으로 채워질 때까지 회전을 계속한다.

다듬은 정십이면체는 깎은 이십이십면체에서 교대 과정을 통해 만들 수도 있다. 깎은 이십이십면체의 꼭짓점 60개는 위상적으로 하나의 다듬은 정십이면체와 동일한 다면체를 형성하며, 나머지 60개는 그 거울상을 형성한다. 결과 다면체는 꼭짓점 추이이지만 균일하지 않다.

2. 2. 지표

한 변의 길이를 ''a''라고 할 때 겉넓이와 외접구의 반지름은 다음과 같다.

'''겉넓이'''
: $(20\sqrt{3}+3\sqrt{25+10\sqrt{5}})a^2$
'''외접구 반지름'''
: $\frac{a}{12}\sqrt{6\left(27+7\sqrt{5}+\sqrt[3]{20448+9140\sqrt{5}-12\sqrt{7137+3192\sqrt{5}}}+\sqrt[3]{20448+9140\sqrt{5}+12\sqrt{7137+3192\sqrt{5}}}\right)}$

다듬은 정십이면체는 모든 아르키메데스 다면체 중에서 가장 높은 구형도를 갖는다. 구형도는 부피의 제곱을 표면적의 세제곱으로 나눈 값에 36π^영어 (π)의 상수를 곱한 값으로 정의되는데(이 상수는 구의 구형도를 1로 만든다), 다듬은 정십이면체의 구형도는 약 0.947이다.^[1]

그 외의 값은 다음과 같다.

꼬임각: 13.1064033769358
준정다면체 중에서 가장 많은 면을 가진다(변과 꼭짓점의 수로는 최대는 능깎이 큰 이십면체이다).

2. 2. 1. 겉넓이

가장자리 길이가 1인 다듬은 정십이면체의 겉넓이는 다음과 같다.^[1]

:

A = 20\sqrt{3} + 3\sqrt{25+10\sqrt{5}} \approx 55.286\,744\,958\,445\,15.

한 변의 길이를 a라고 할 때 겉넓이는 다음과 같다.

:

(20\sqrt{3}+3\sqrt{25+10\sqrt{5}})a^2

2. 2. 2. 부피

φ^영어는 황금비, ξ^영어 ≈ 0.94315125924일 때, 가장자리 길이가 1인 다듬은 정십이면체의 부피는 다음과 같다.^[1]

:

V= \frac{(3\varphi+1)\xi^2+(3\varphi+1)\xi-\varphi/6-2}{\sqrt{3\xi^2-\varphi^2}}\approx 37.616\,649\,962\,733\,36.

또는, 이 부피는 다음과 같이 쓸 수 있다.^[1]

:

\begin{align}V &= \frac{5+5\sqrt{5}}{6\sqrt{3}}\sqrt} + {a \left({3+3\sqrt{5}} + a \right)} }+\frac{5+3\sqrt{5}}{24\sqrt{2}}\sqrt{ 72 + {\left({5+\sqrt{5}}\right)}a \left(} + a \right)} \\[2pt]&\approx 37.616\,649\,962\,733\,36,\end{align}

여기서,^[1]

:

\begin{align}a &= \sqrt[3]{54(1+\sqrt{5})+6\sqrt{102+162\sqrt{5}}}+\sqrt[3]{54(1+\sqrt{5})-6\sqrt{102+162\sqrt{5}}} \\[2pt]&\approx 10.293\,368\,998\,184\,21.\end{align}

2. 2. 3. 외접구 반지름

가장자리 길이가 1인 다듬은 정십이면체의 외접구 반지름은 다음과 같다.

:

R = \frac12\sqrt{\frac{2-\xi}{1-\xi}} \approx 2.155\,837\,375.

이 값은 다음 6차 방정식의 네 개의 양의 실수 근 중 하나(''R''²)이다.

:

4096R^{12} - 27648R^{10} + 47104R^8 - 35776R^6 + 13872R^4 - 2696R^2 + 209 = 0

이 방정식은 다듬은 정십이면체(''U''₂₉), 큰 엇깎은 이십이십이면체(''U''₅₇), 큰 역엇깎은 이십이십이면체(''U''₆₉) 및 큰 역엇깎은 이십이십이면체(''U''₇₄)의 외접구 반지름을 나타내는 방정식이다.

한 변의 길이를 a라고 할 때, 외접구 반지름은 다음과 같이 나타낼 수 있다.

:

\frac{a}{12}\sqrt{6\left(27+7\sqrt{5}+\sqrt[3]{20448+9140\sqrt{5}-12\sqrt{7137+3192\sqrt{5}}}+\sqrt[3]{20448+9140\sqrt{5}+12\sqrt{7137+3192\sqrt{5}}}\right)}

2. 3. 직교 투영

'''다듬은 정십이면체'''는 삼각형과 오각형을 중심으로 하는 두 개의 특히 대칭적인 직교 투영을 가지며, 이는 A₂ 및 H₂ 콕서 평면에 해당한다. 아래 표에 이 직교 투영들이 나타나 있다.

직교 투영
중심	면 삼각형	면 오각형	모서리
입체
와이어프레임	120px	120px	120px
사영 대칭	[3]	[5]	[2]
쌍대	120px	120px	120px

3. 데카르트 좌표

ξ^영어 ≈ 0.94315125924를 삼차 다항식 ''x''³ + 2''x''² − ''φ''²의 실수 근이라고 하자. 여기서 ''φ''는 황금비이다. 점 ''p''는 다음과 같다.

$p=\begin{pmatrix}\varphi^2-\varphi^2\xi \\$

\varphi^3+\varphi\xi+2\varphi\xi^2 \\

\xi\end{pmatrix}.

회전 행렬 ''M''₁과 ''M''₂는 다음과 같다.

M_1=\begin{pmatrix}\frac{1}{2\varphi}  & -\frac{\varphi}{2} & \frac{1}{2} \\\frac{\varphi}{2}   & \frac{1}{2}     & \frac{1}{2\varphi} \\

\frac{1}{2} & \frac{1}{2\varphi} & \frac{\varphi}{2}

\end{pmatrix}, \quad M_2=\begin{pmatrix}0 & 0 & 1 \\1 & 0 & 0 \\0 & 1 & 0\end{pmatrix}.

''M''₁은

\tfrac{2\pi}{5}

의 각도로 (0, 1, ''φ'') 축을 중심으로 반시계 방향으로 회전하는 것을 나타내며, ''M''₂는

\tfrac{2\pi}{3}

의 각도로 (1, 1, 1) 축을 중심으로 회전하는 것을 나타낸다. 그러면 깎은 정십이면체의 60개 꼭짓점은 ''M''₁ 및/또는 ''M''₂를 반복적으로 곱하여 수렴하도록 점 ''p''를 변환한 60개의 이미지이다. (행렬 ''M''₁과 ''M''₂는 정규 20면체의 60개 회전 대칭에 해당하는 60개의 회전 행렬을 생성한다.) 꼭짓점의 좌표는 1, ''φ'', ''ξ'', ''φξ'', ''ξ''² 및 ''φξ''²의 정수 선형 결합이다. 모서리 길이는 다음과 같다.

2\xi\sqrt{1-\xi}\approx 0.449\,750\,618\,41.

모든 좌표의 부호를 바꾸면 이 깎은 정십이면체의 거울상 이미지가 된다.

4. 관련 다면체 및 타일링

다듬은 정십이면체는 정십이면체의 열두 오각형 면을 서로 닿지 않도록 바깥쪽으로 당겨서 만들 수 있다. 적절한 거리에서 분할된 변 사이에 사각형 면을 채우고, 분할된 꼭짓점 사이에 삼각형 면을 채워 롬비이십면체를 만들 수 있다. 하지만 엇깎인 형태(다듬은 정십이면체)의 경우 오각형 면을 약간 덜 당기고 삼각형 면만 추가하여 다른 간격은 비워둔다. 그런 다음 오각형과 삼각형의 중심에 동일한 회전을 적용하여 간격이 두 개의 정삼각형으로 채워질 때까지 회전을 계속한다.

다듬은 정십이면체는 깎은 이십이십면체에서 교대 과정을 통해 파생될 수도 있다. 깎은 이십이십면체의 꼭짓점 60개는 위상적으로 하나의 다듬은 정십이면체와 동일한 다면체를 형성하며, 나머지 60개는 그 거울상을 형성한다.

이 다면체는 꼭짓점 도형 (3.3.3.3.n)을 갖는 일련의 깎은 다면체 및 타일링의 일원이다. 이러한 도형과 그 쌍대는 (n32) 회전 대칭을 가지며, n = 6일 때는 유클리드 평면에, 그보다 큰 모든 n에 대해서는 쌍곡 평면에 존재한다.

이름	이미지	꼭짓점 도형
깎은 이십이십이면체	--	(3.3.3.3.5)
깎은 십이면체	--	(3.3.3.5.3.5)
정십이면체		{5, 3}
정이십면체		{3, 5}
이십이십이면체	--	r{5, 3}

5. 깎은 정십이면체 그래프

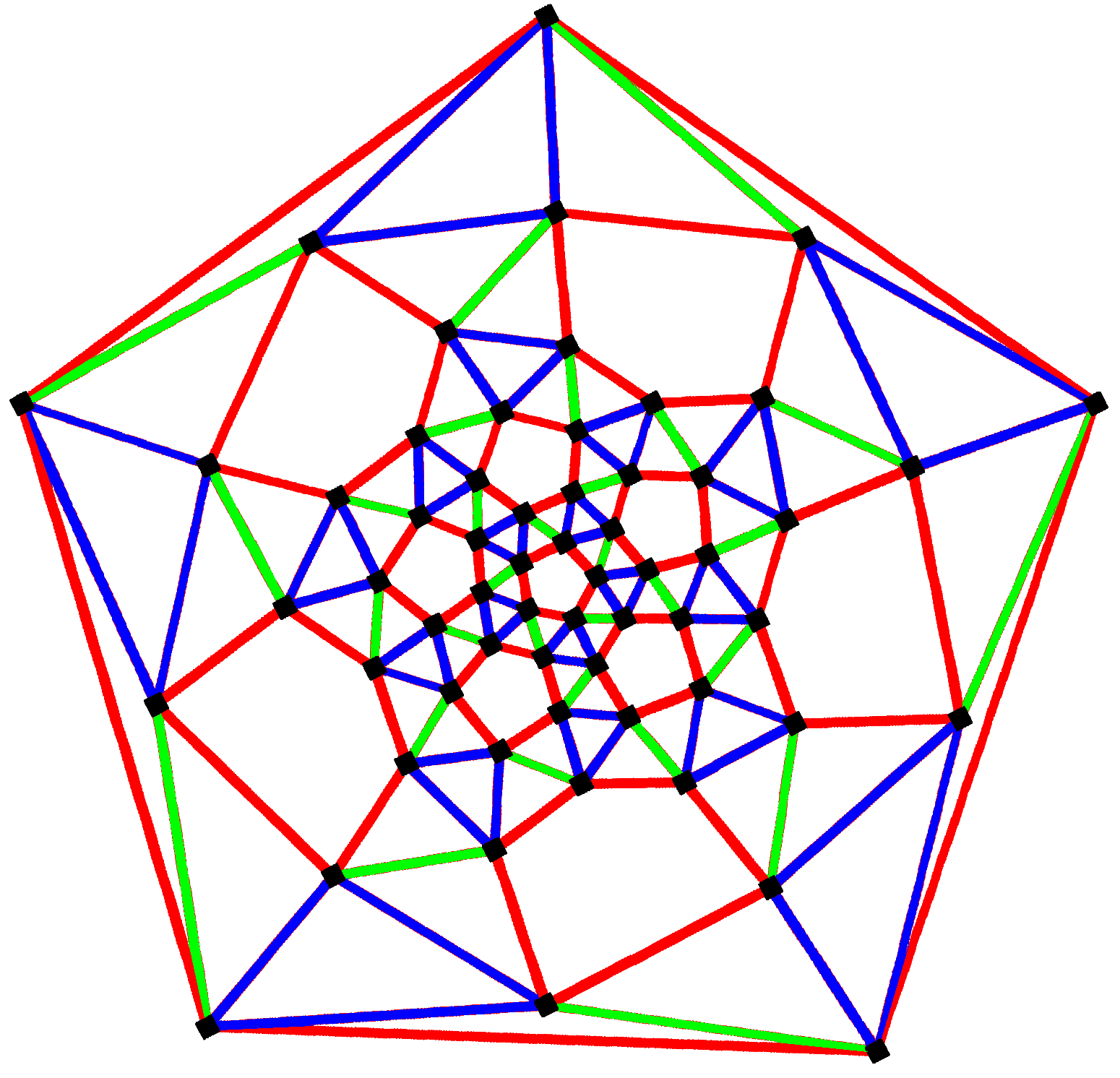
그래프 이론에서 '''깎은 정십이면체 그래프'''는 깎은 정십이면체의 꼭짓점과 모서리를 나타내는 그래프이다. 60개의 꼭짓점과 150개의 모서리를 가지며, 아르키메데스 그래프이다.^[2]

참조

_[1] 논문 How Spherical Are the Archimedean Solids and Their Duals? 2011-03
_[2] 서적 An Atlas of Graphs Oxford University Press

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com